2. Geometrian peruskäsitteitä
Tasogeometriassa tutkitaan tasokuvioita ja niiden ominaisuuksia. Peruskäsitteitä ovat piste ja suora.
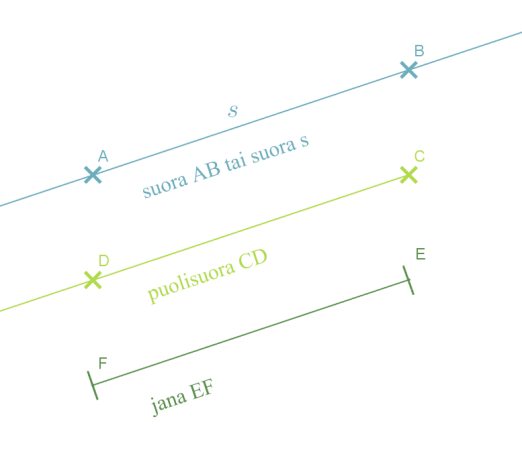
Pisteellä on paikka, mutta ei ulottuvuutta. Pisteellä ei siis ole pituutta, leveyttä eikä korkeutta. Sitä kuvataan pienellä ympyrällä tai rastilla. Piste sijaitsee tällöin ympyrän keskipisteessä tai rastin osien leikkauskohdassa. Pisteiden niminä käytetään yleensä isoja kirjaimia. Koska jokaisella pisteellä on oma paikkansa, ei samassa kuvassa voi olla kahta samannimistä pistettä.
Kahden pisteen kautta voidaan piirtää vain yksi suora, joka nimetään joko pisteiden mukaan tai pienellä kirjaimella. Vaikka suoralla on pituus, ei sitä voida mitata, koska suora jatkuu molempiin suuntiin loputtomasti.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Geometrian peruskäsitteiden määritelmiä
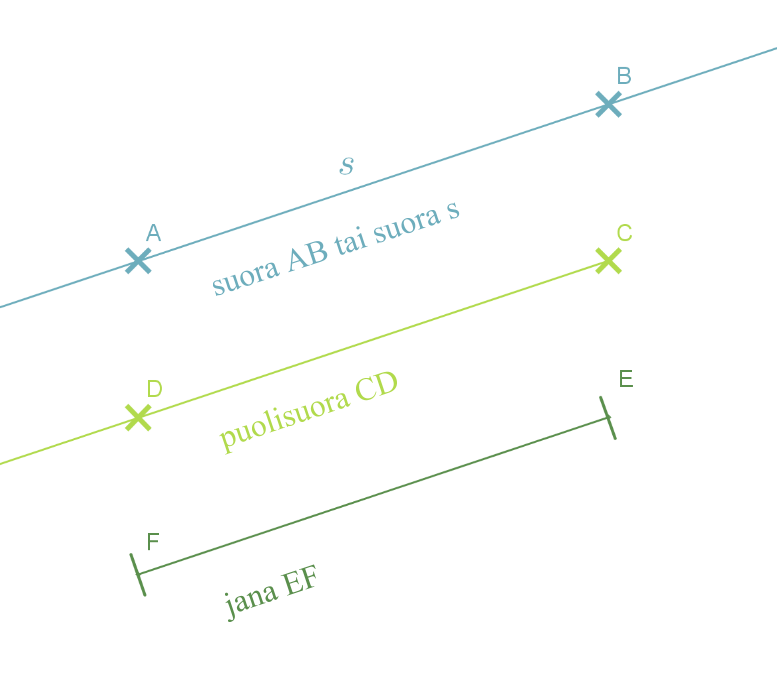
- Pisteestä alkavaa, toiseen suuntaan rajattomasti jatketuksi ajateltua suoraa sanotaan puolisuoraksi.
- Jana on kahden pisteen välinen suoran osa.
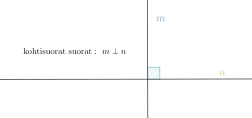
- Jos kaksi suoraa on kohtisuorassa toisiaan vastaan, niitä sanotaan toistensa normaaleiksi. Kohtisuoruutta merkitään symbolilla ⊥.
- Yhdensuuntaiset suorat eivät leikkaa tosiaan. Yhdensuuntaisuutta merkitään symbolilla ||.
- Janan keskinormaali on suora, joka kulkee janan keskipisteen kautta ja on kohtisuorassa janaa vastaan.
Klikkaa kuva suuremmaksi!
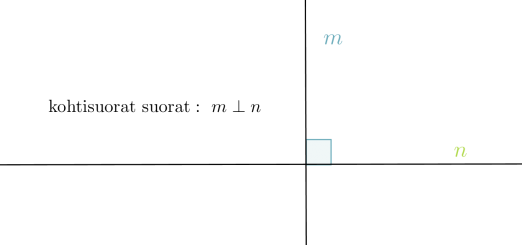
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
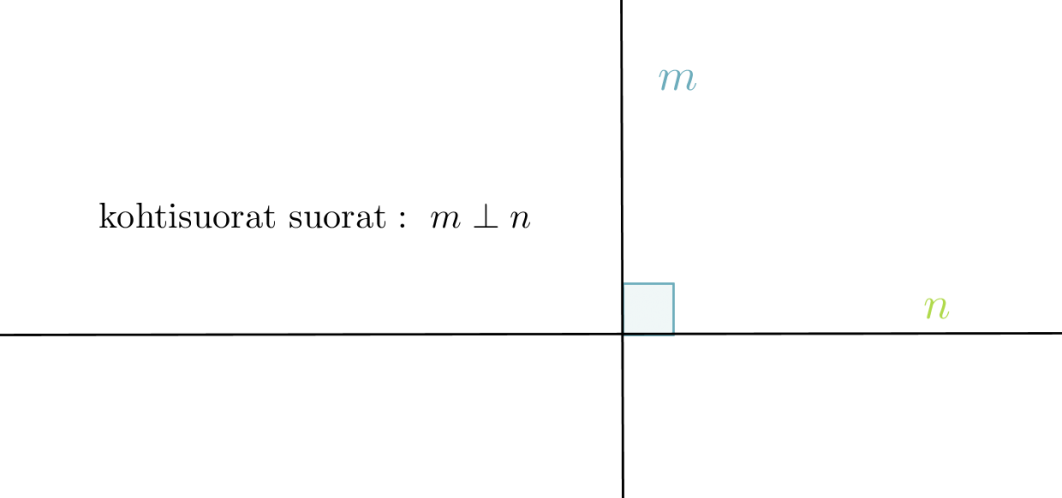
Klikkaa kuva suuremmaksi!
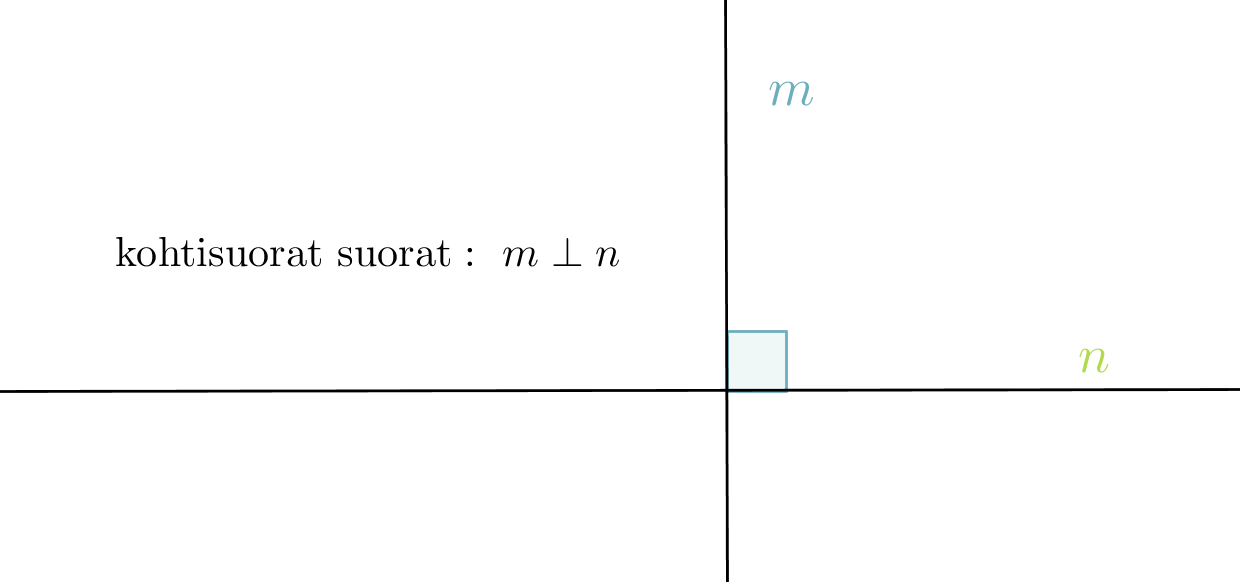
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
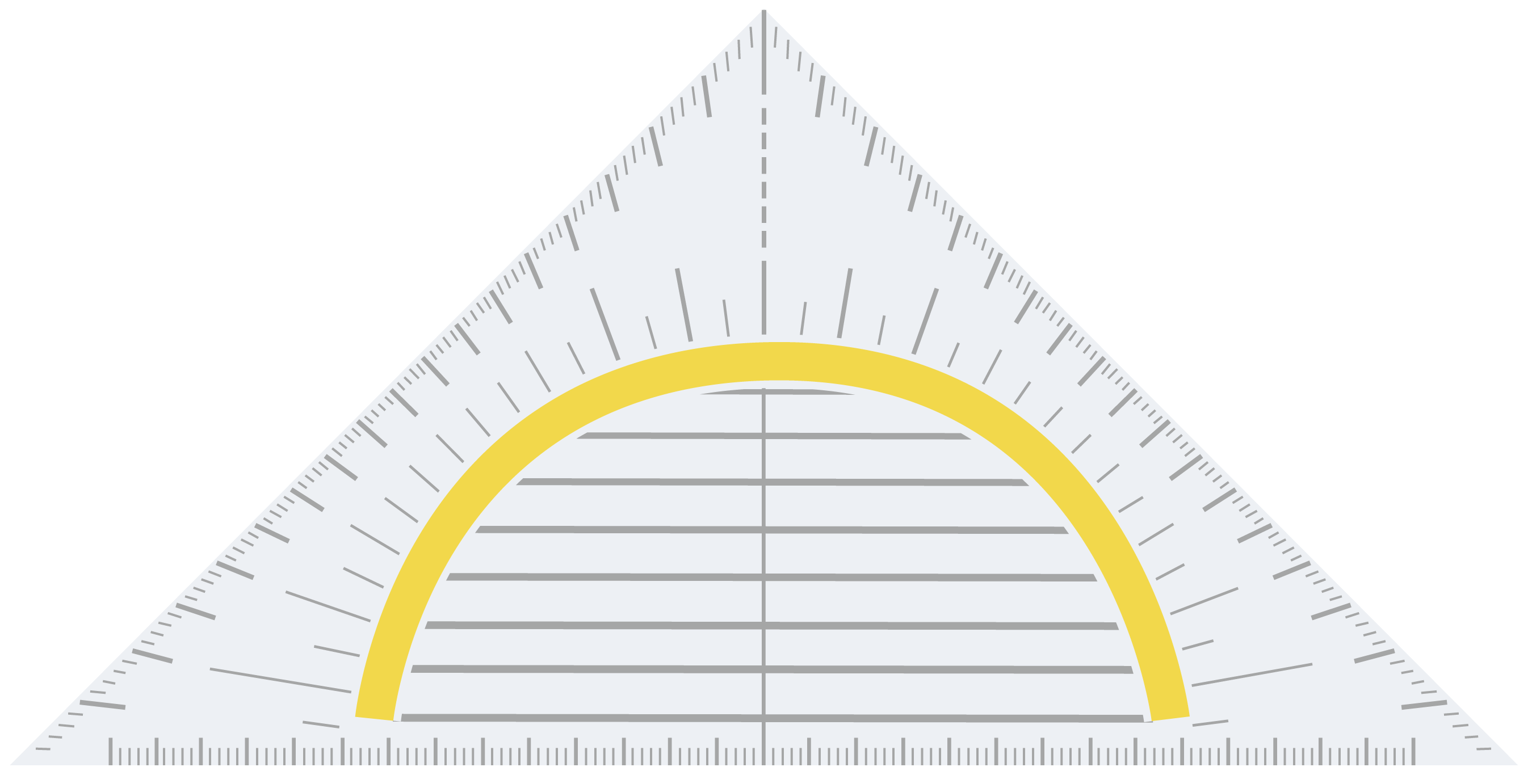
Piirtokolmion käyttö
Piirtokolmion yhdensuuntaisten apuviivojen sekä piirtokolmion kantaa vastaan kohtisuorassa olevan korkeusjanan avulla on helppo piirtää sekä yhdensuuntaisia suoria että toisiaan vastaan kohtisuorasti sijaitsevia suoria.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
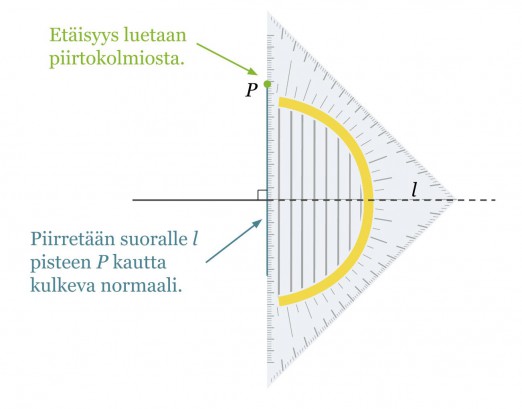
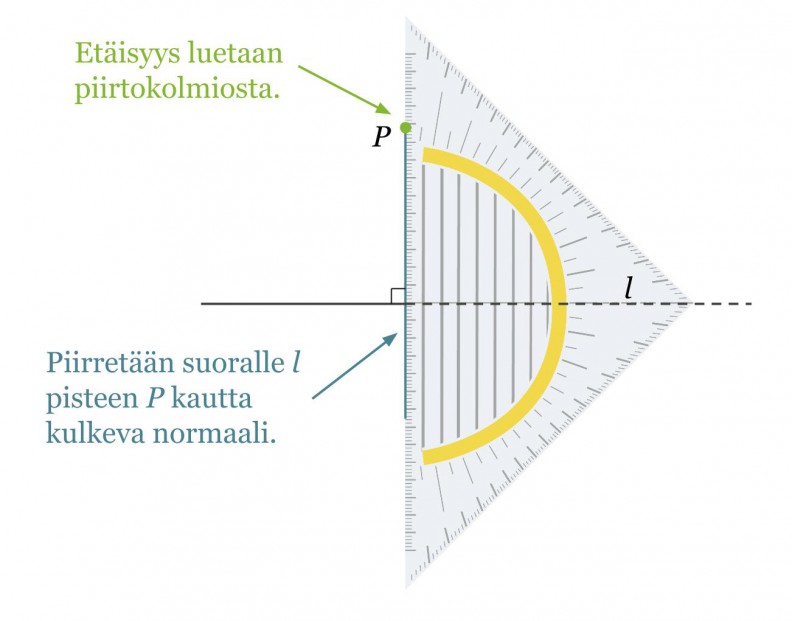
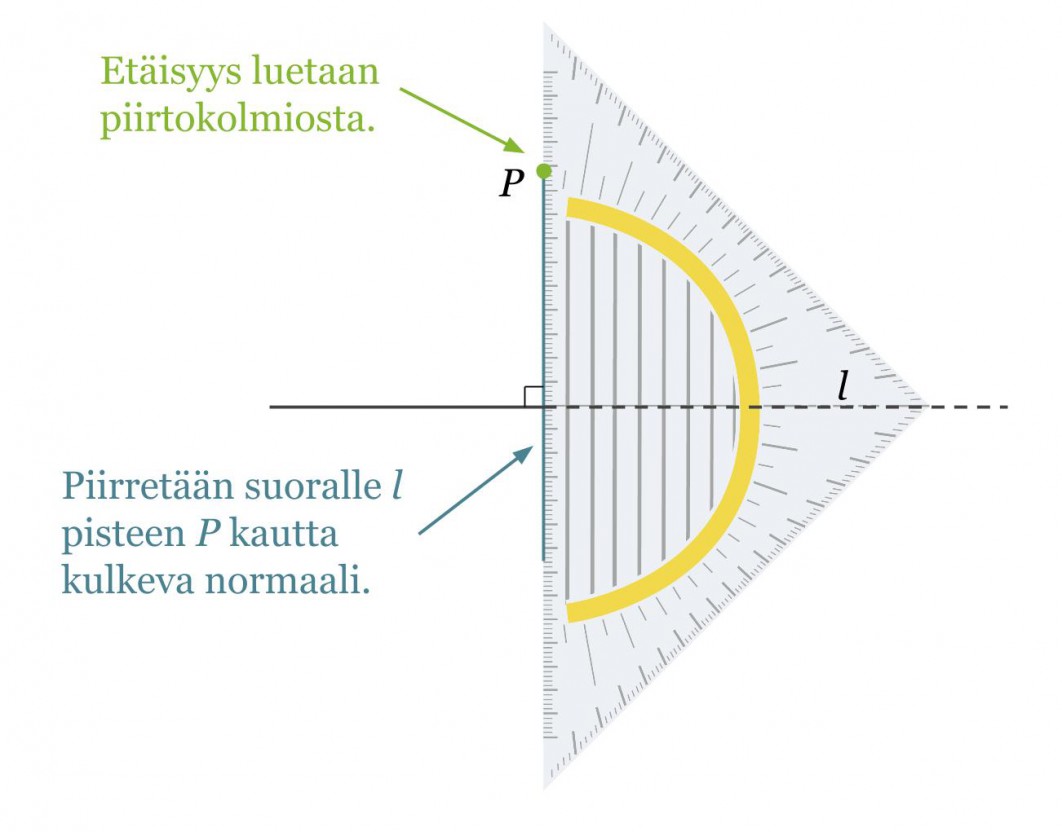
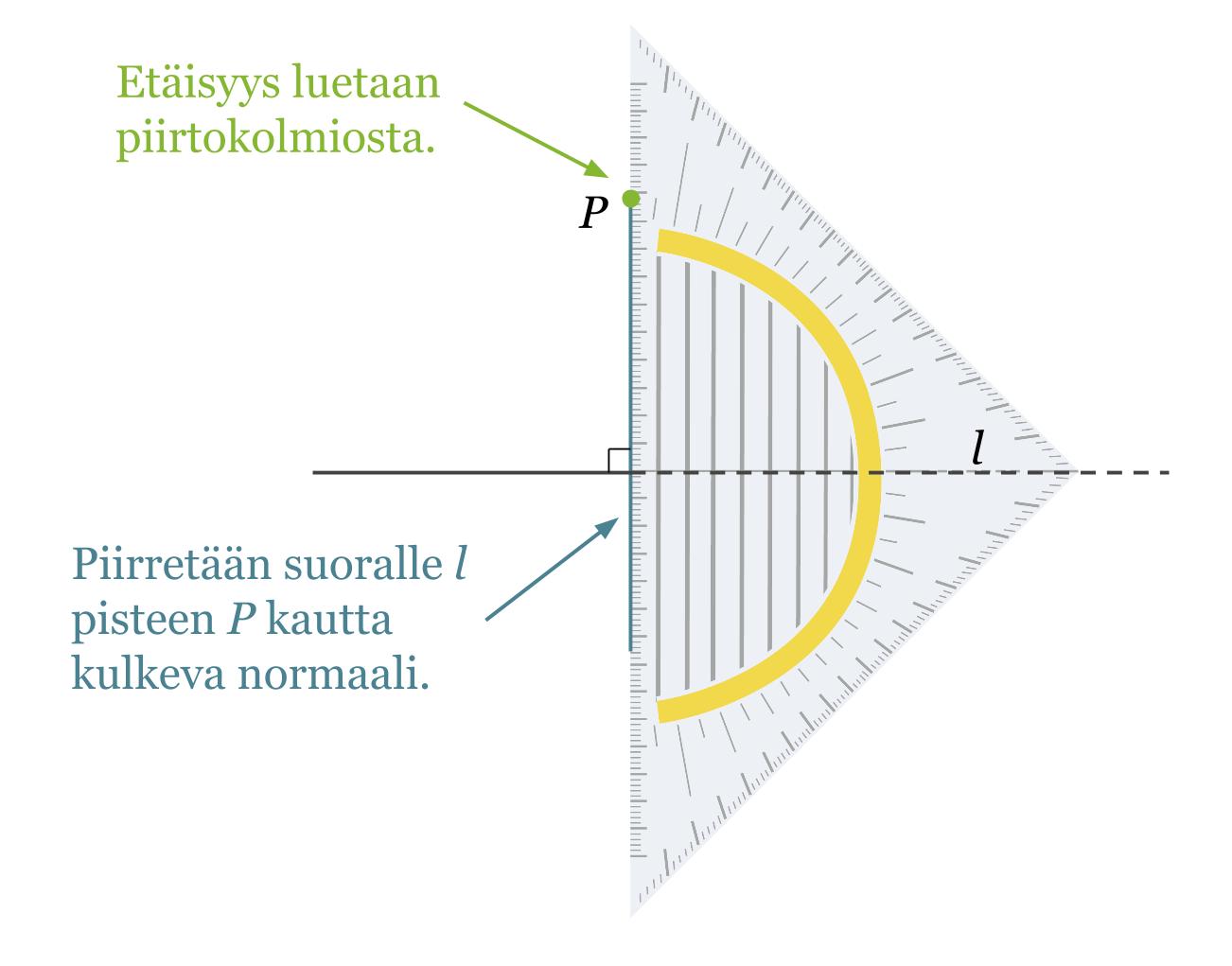
Esimerkki 1.
Määritetään pisteen P kohtisuora etäisyys suorasta l.
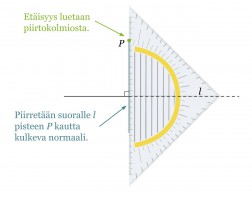
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
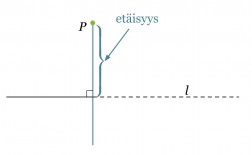
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
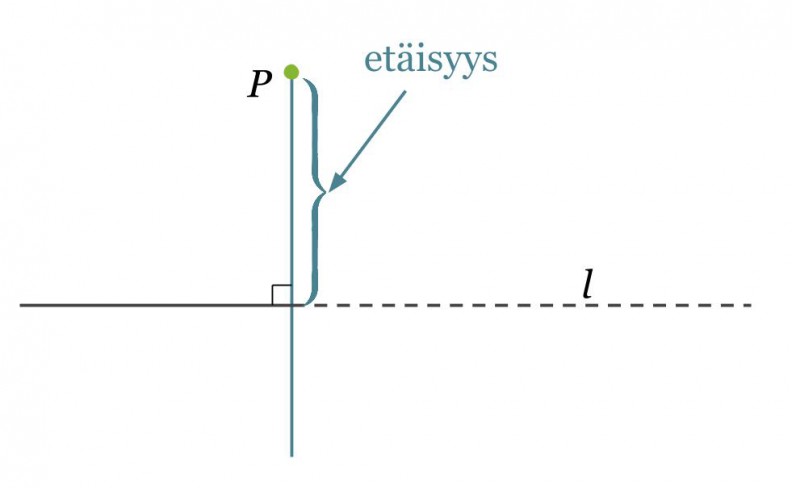
Klikkaa kuva suuremmaksi!
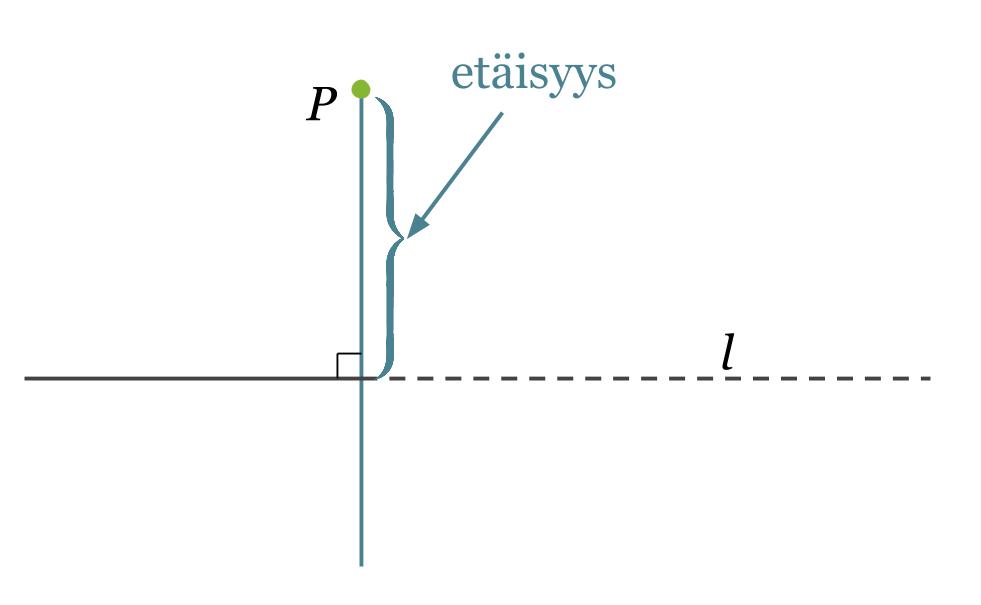
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
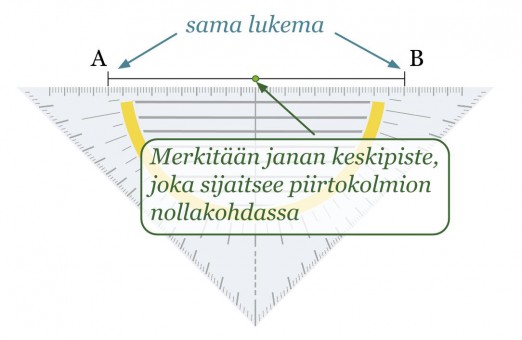
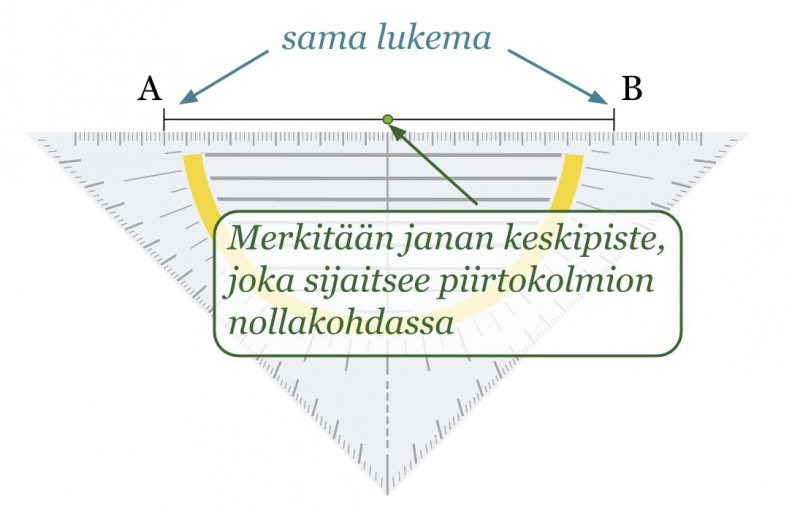
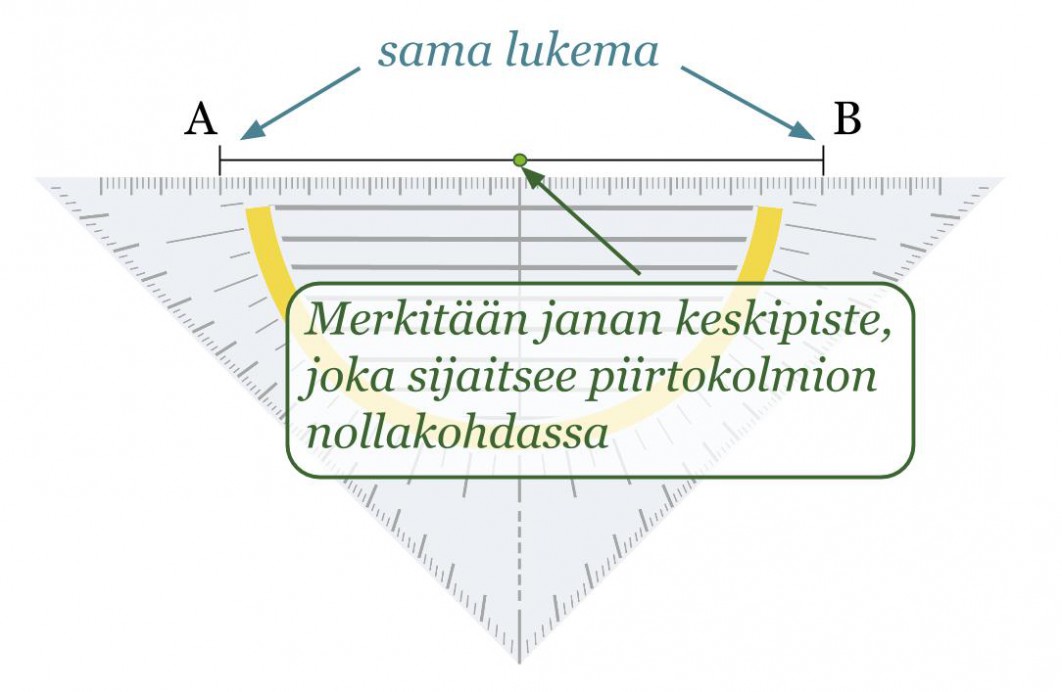
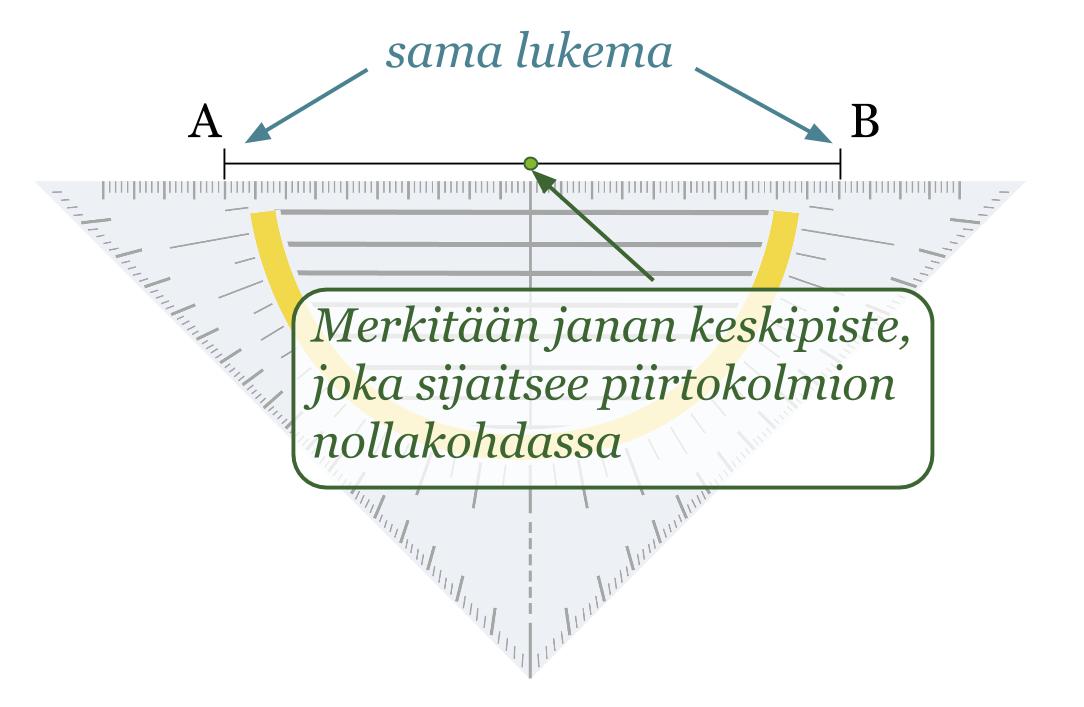
Esimerkki 2.
Piirretään janalle AB keskinormaali.
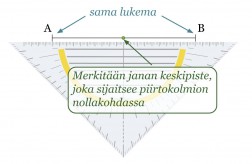
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
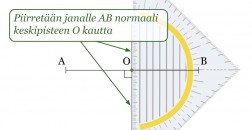
Klikkaa kuva suuremmaksi!
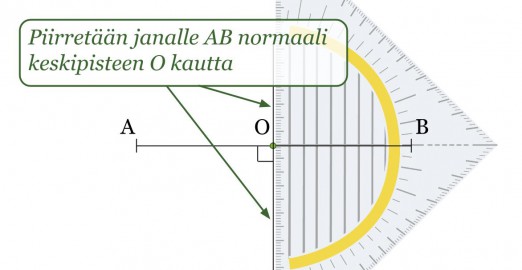
Klikkaa kuva suuremmaksi!
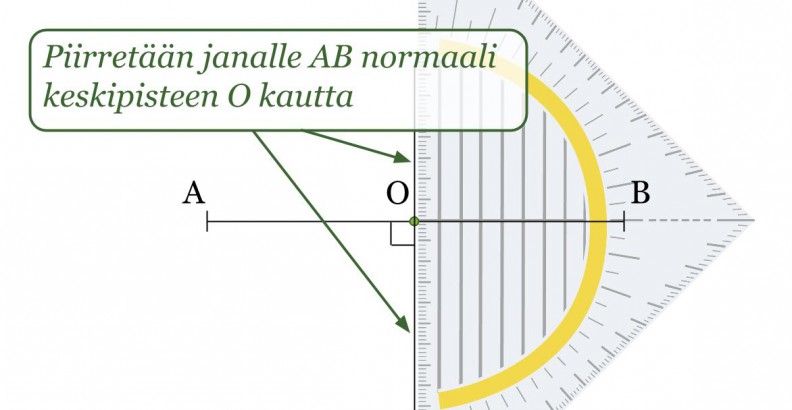
Klikkaa kuva suuremmaksi!
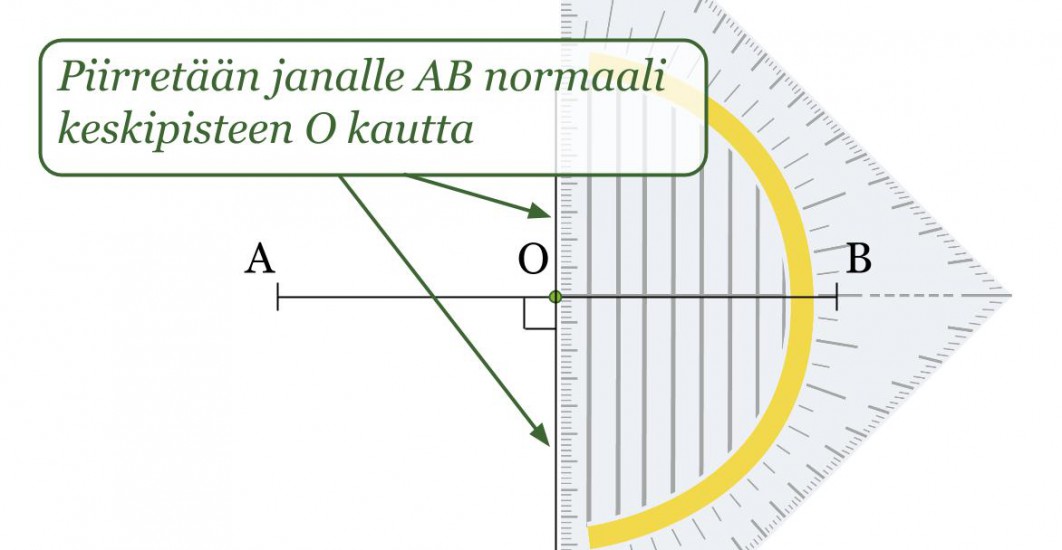
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jos jana on piirretty koordinaatistoon, saadaan janan keskipisteen koordinaatit selville myös laskemalla janan päätepisteiden x– ja y-koordinaattien keskiarvo.
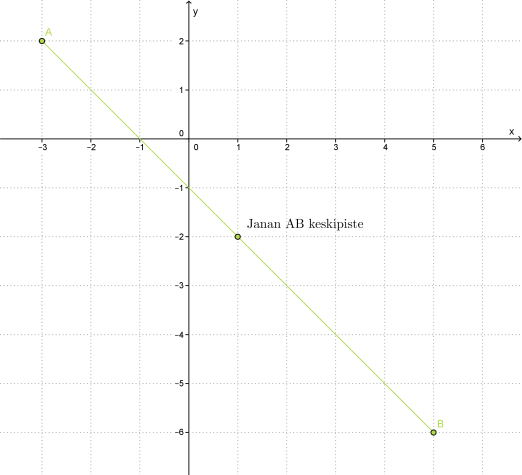
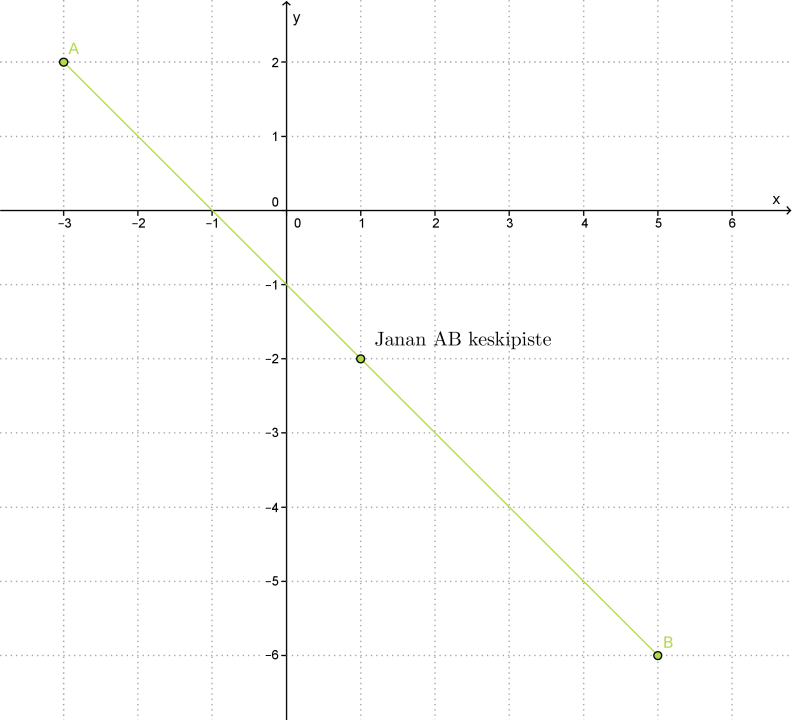
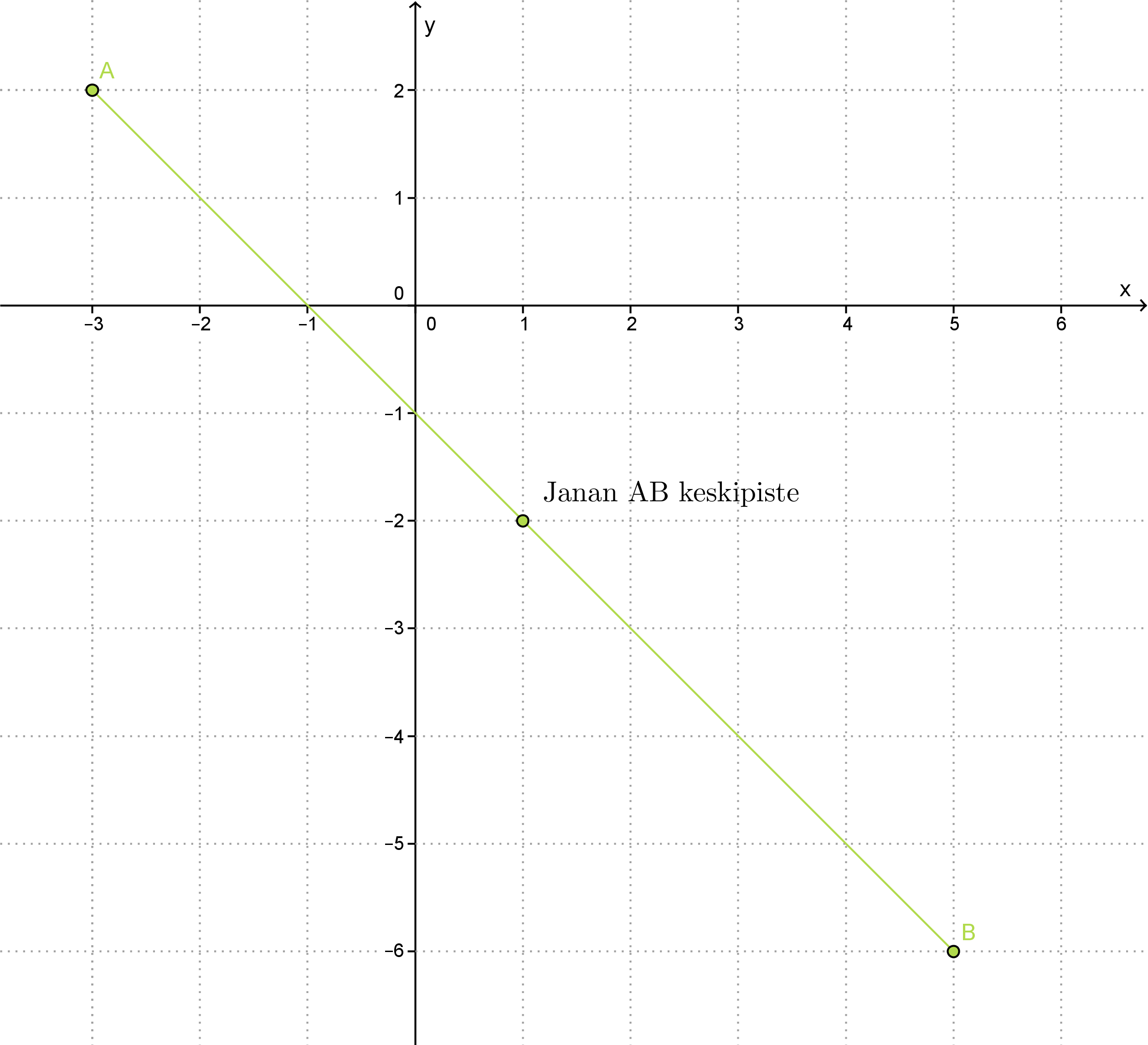
Esimerkki 3.
Lasketaan janan AB keskipisteen koordinaatit, kun A = (−3, 2) ja B = (5, −6).
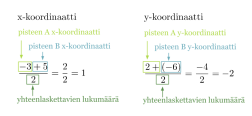
Klikkaa kuvaa suuremmaksi!
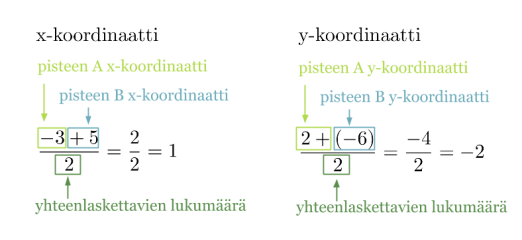
Klikkaa kuvaa suuremmaksi!
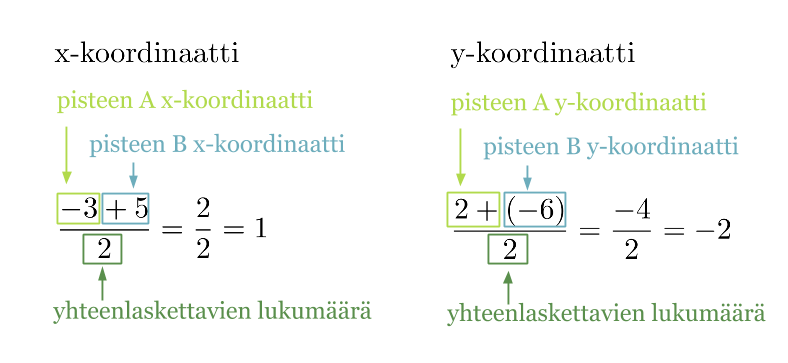
Klikkaa kuvaa suuremmaksi!

Klikkaa kuvaa suuremmaksi!
Vastauksen voi tarkistaa piirtämällä.
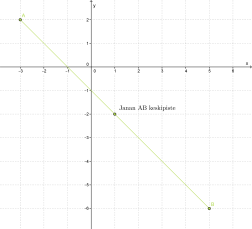
Klikkaa kuvaajaa suuremmaksi!
Klikkaa kuvaajaa suuremmaksi!
Klikkaa kuvaajaa suuremmaksi!

Klikkaa kuvaajaa suuremmaksi!
Klikkaa kuvaajaa suuremmaksi!

Klikkaa kuvaajaa suuremmaksi!
Vastaus: Janan AB keskipiste on (1, -2).