7. Piirretään harpin avulla
Geometrisessa piirtämisessä työvälineinä ovat harppi ja viivain. Viivainta käytetään ainoastaan suorien viivojen piirtämiseen. Mittaamiset suoritetaan harpilla, jolla voidaan erottaa yhtä pitkiä janoja.
Kulman puolittaminen
Puolitetaan annettu kulma.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
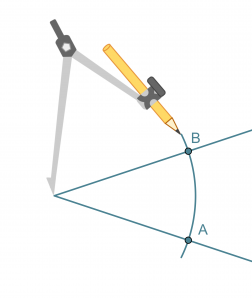
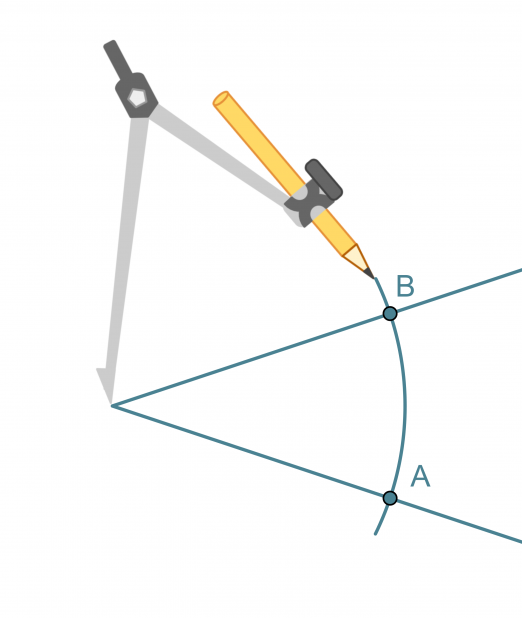
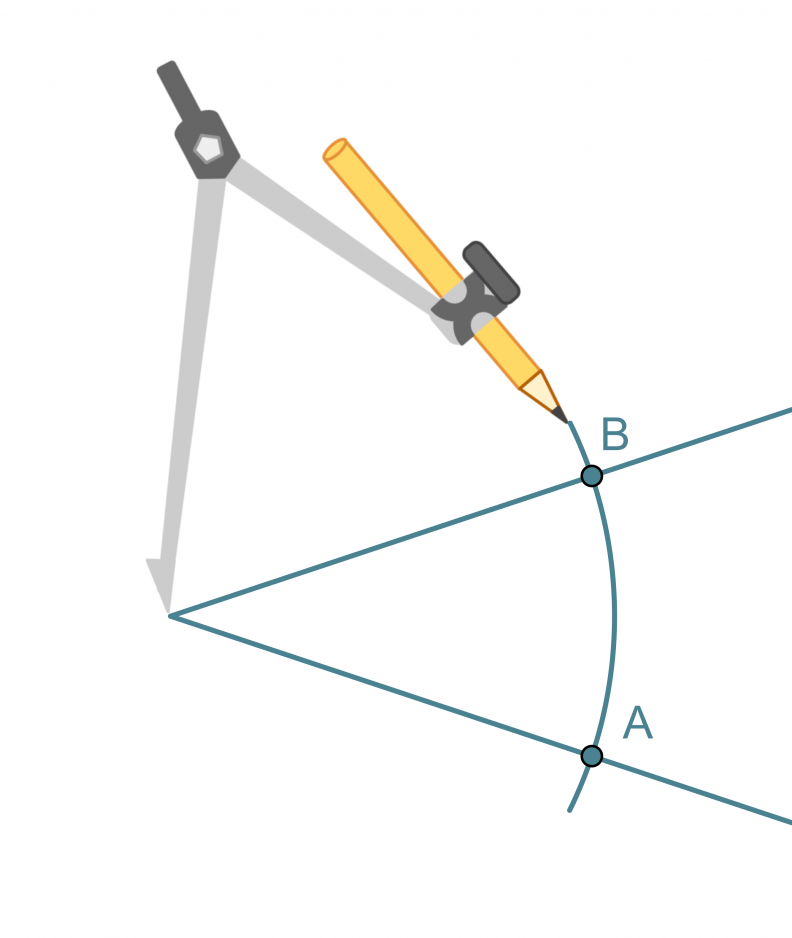
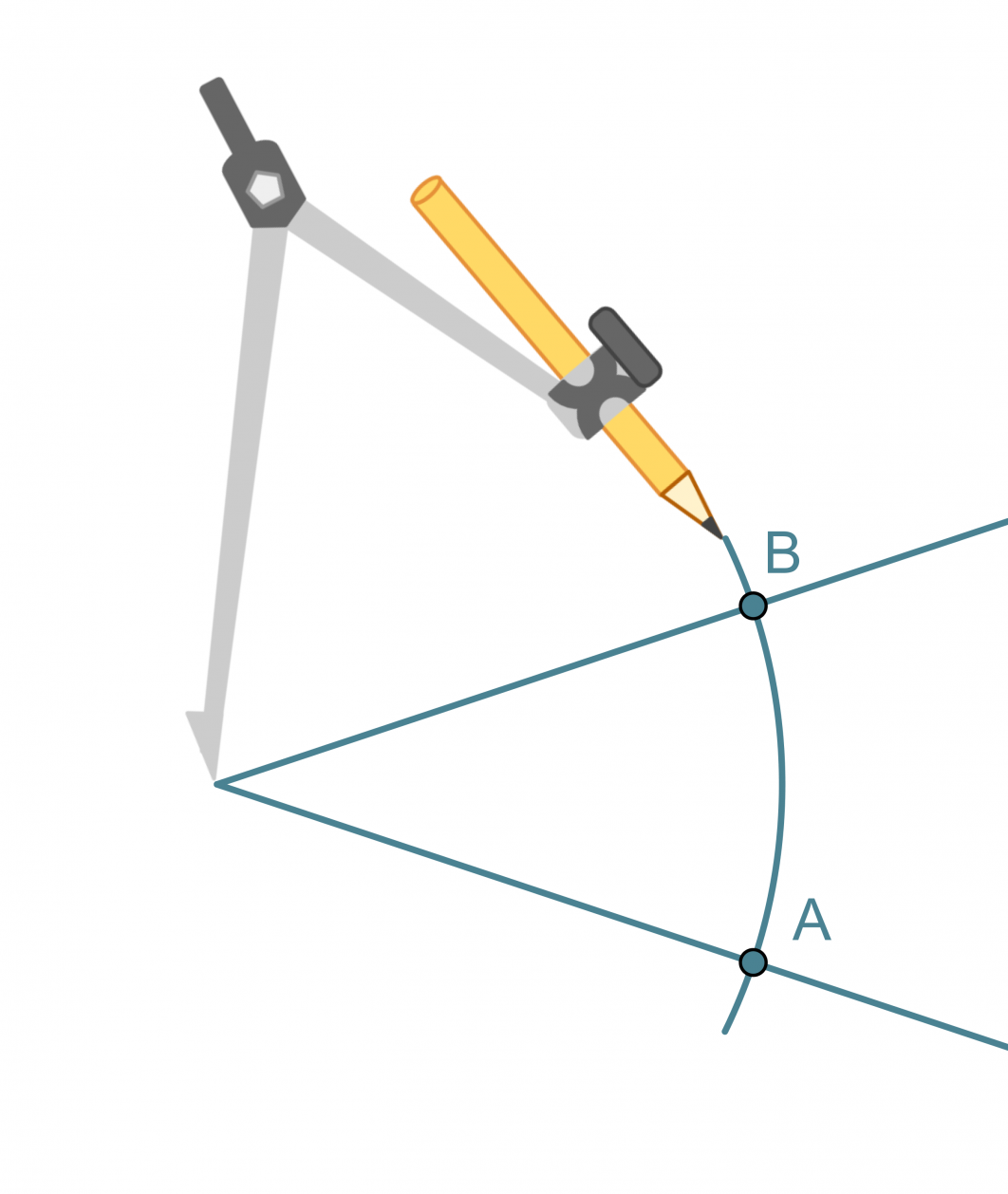
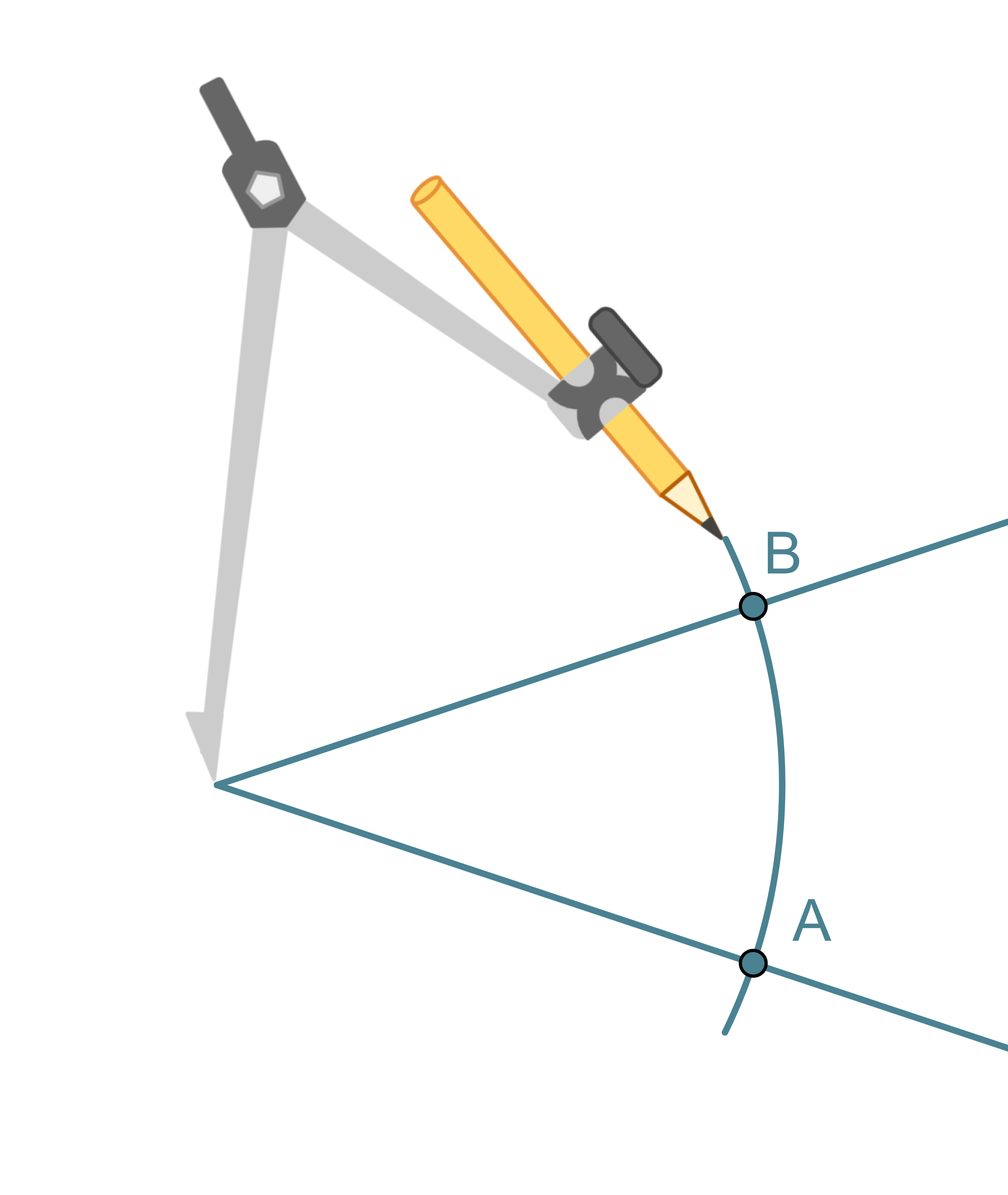
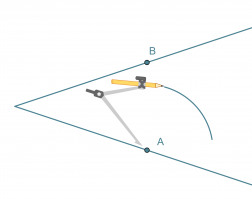
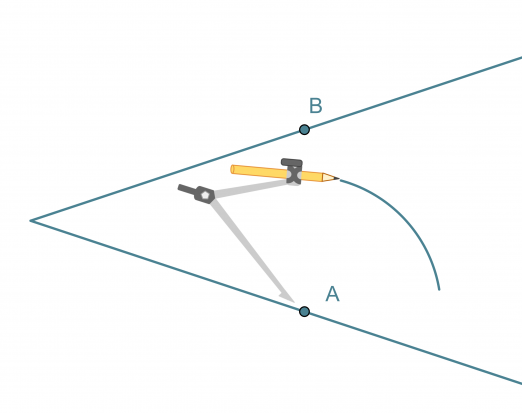
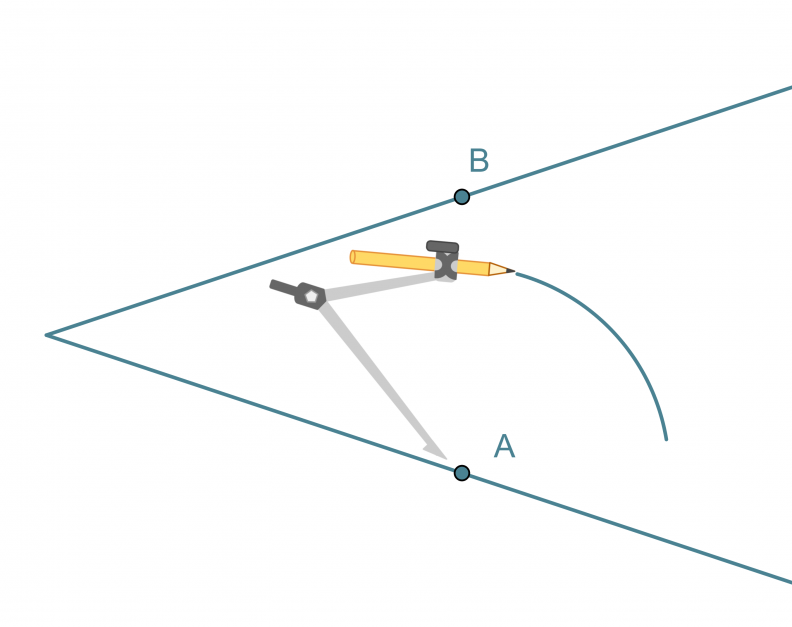
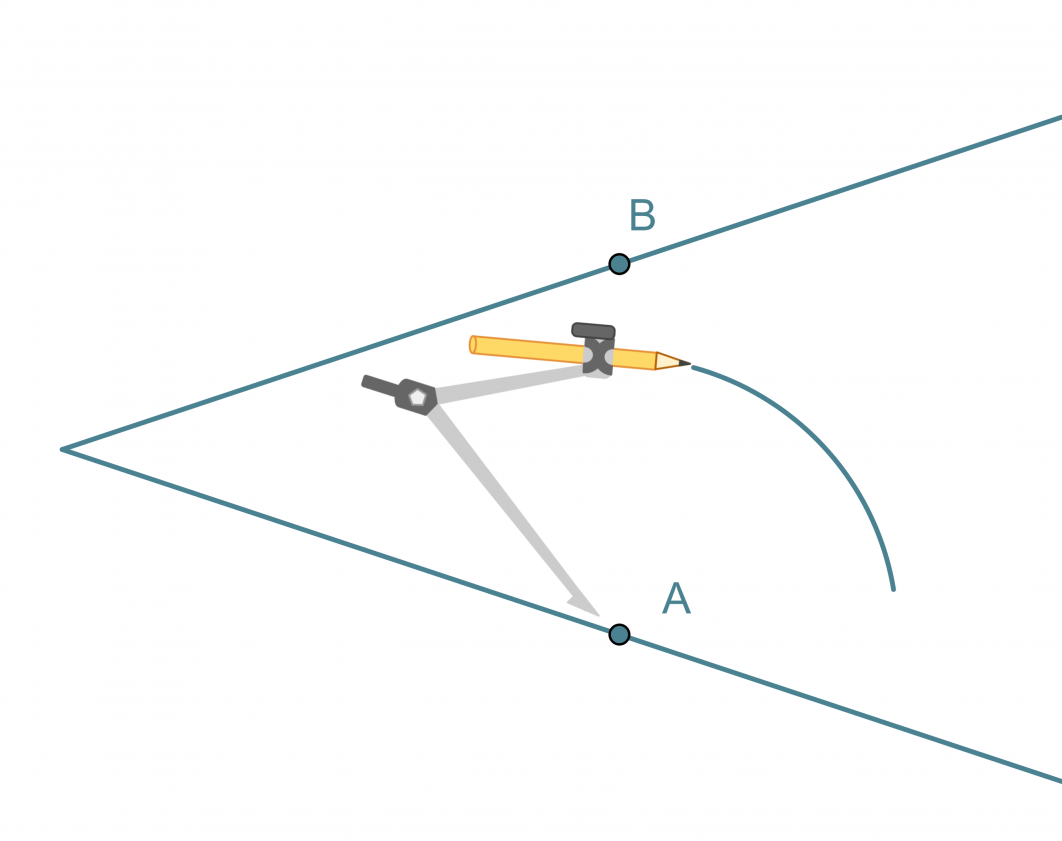
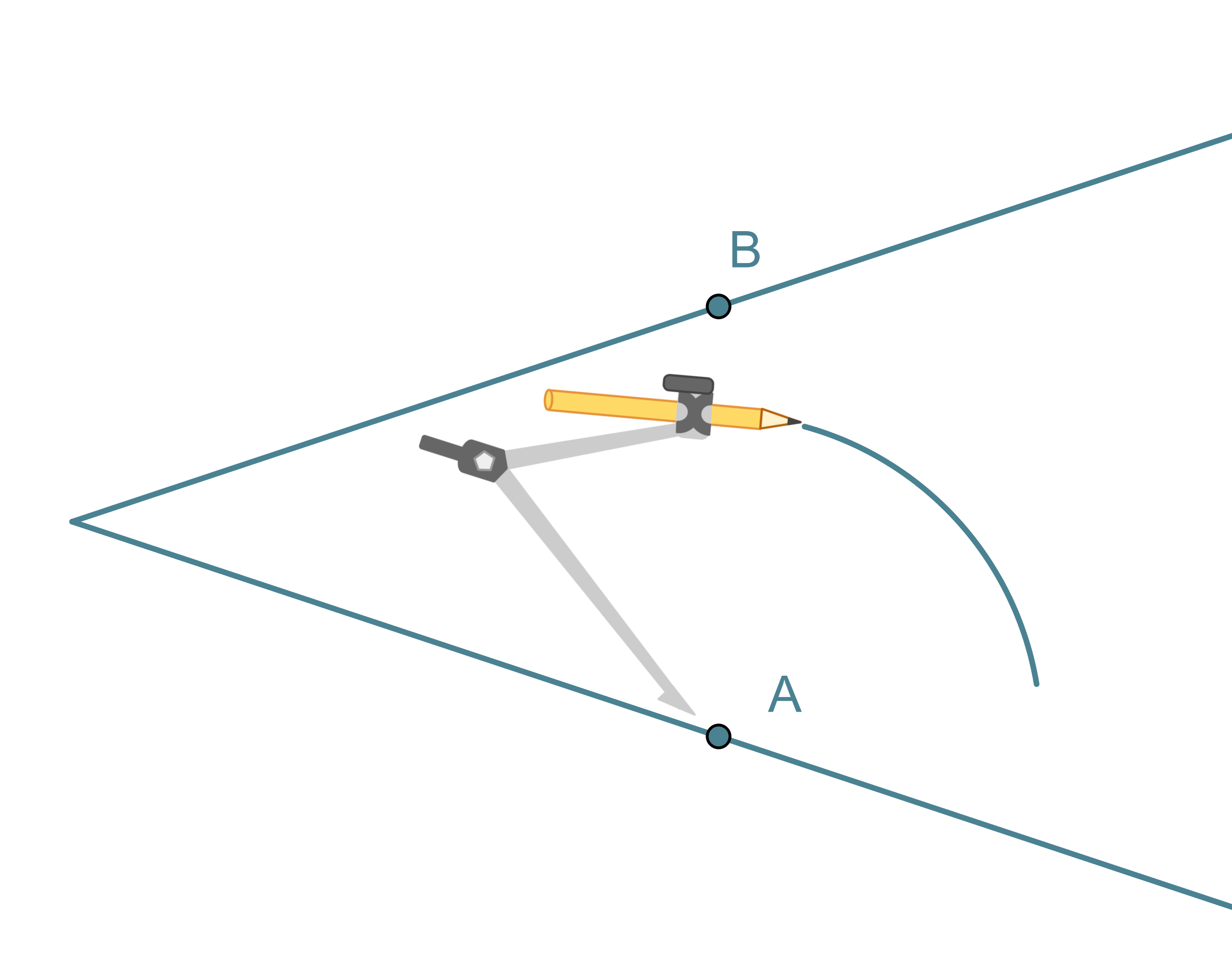
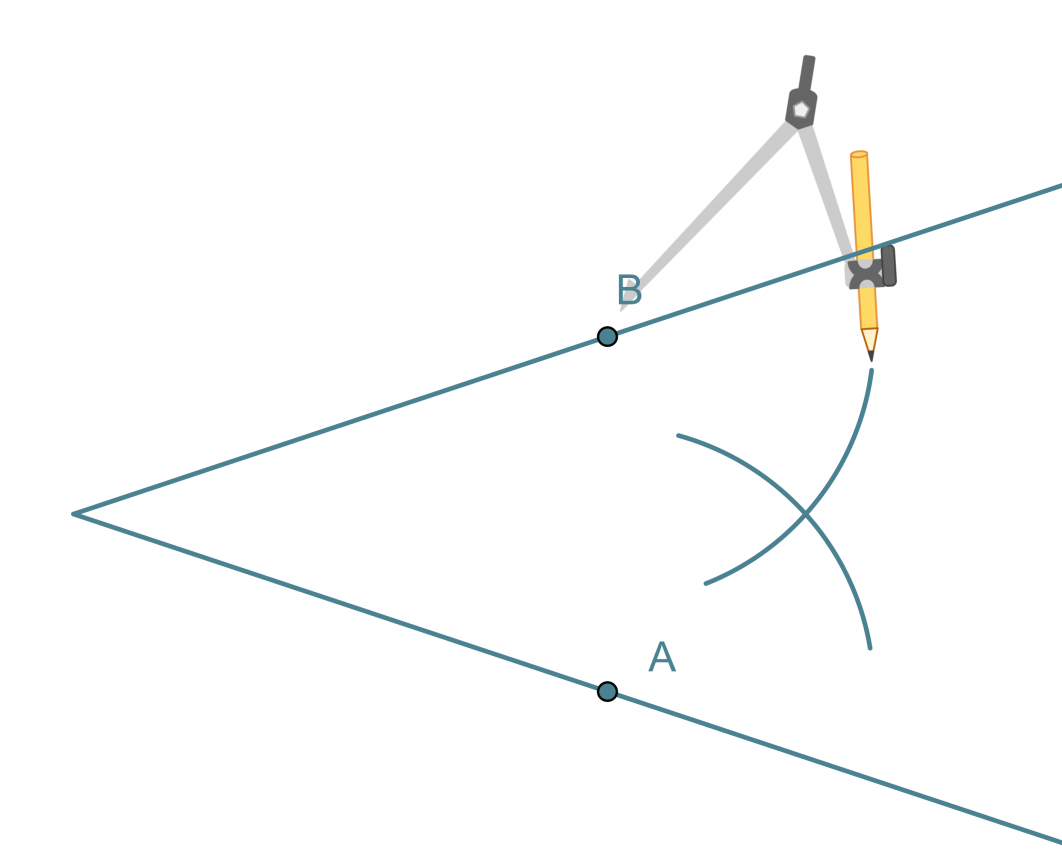
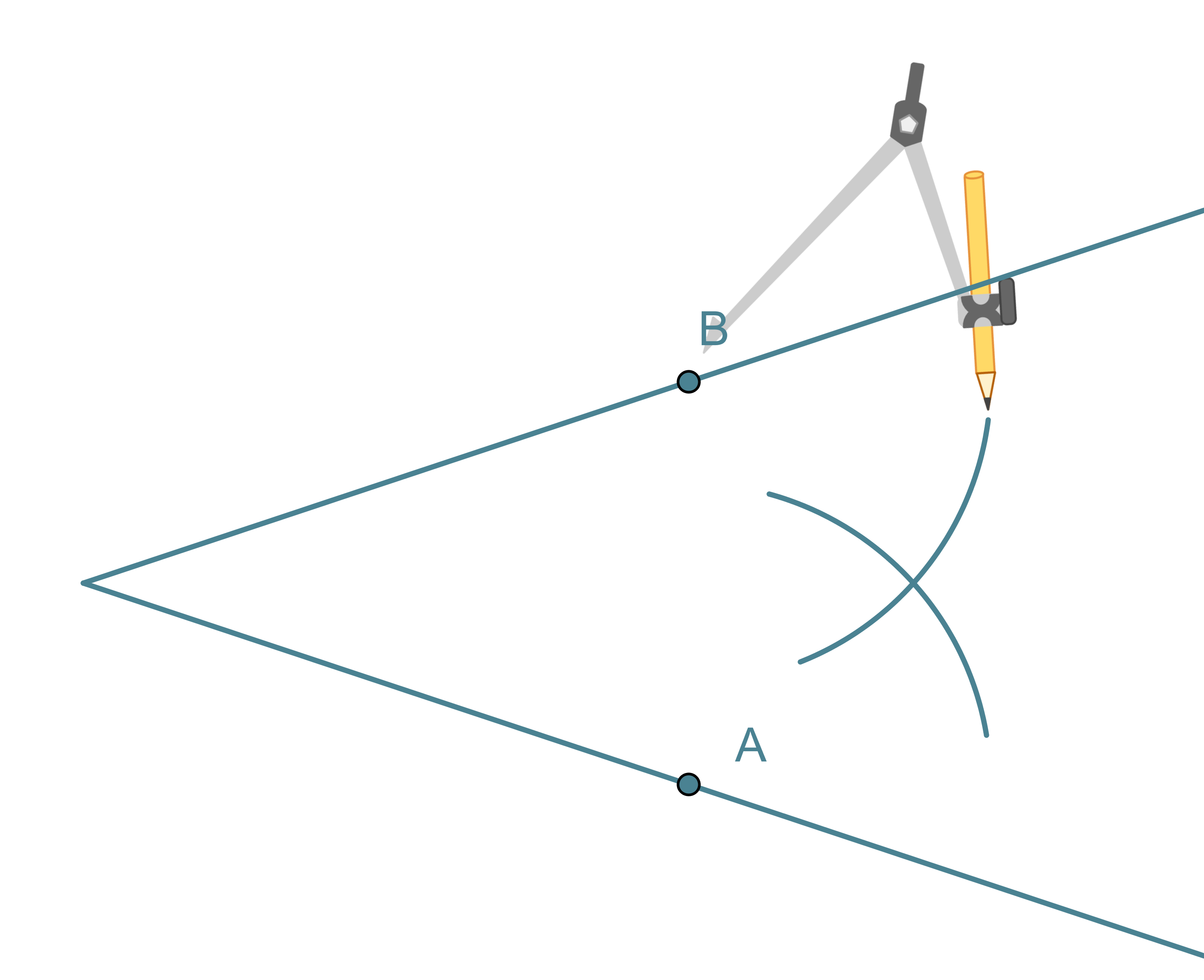
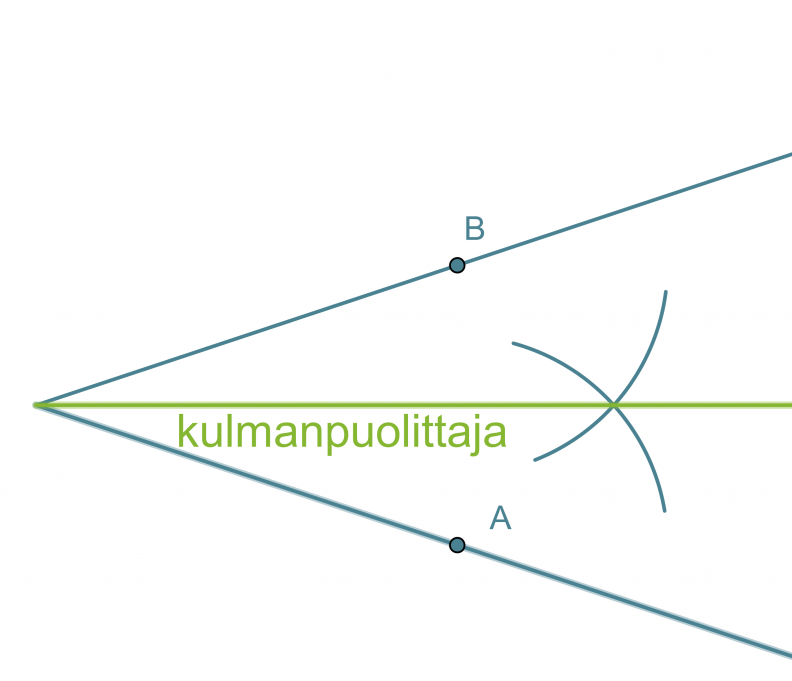
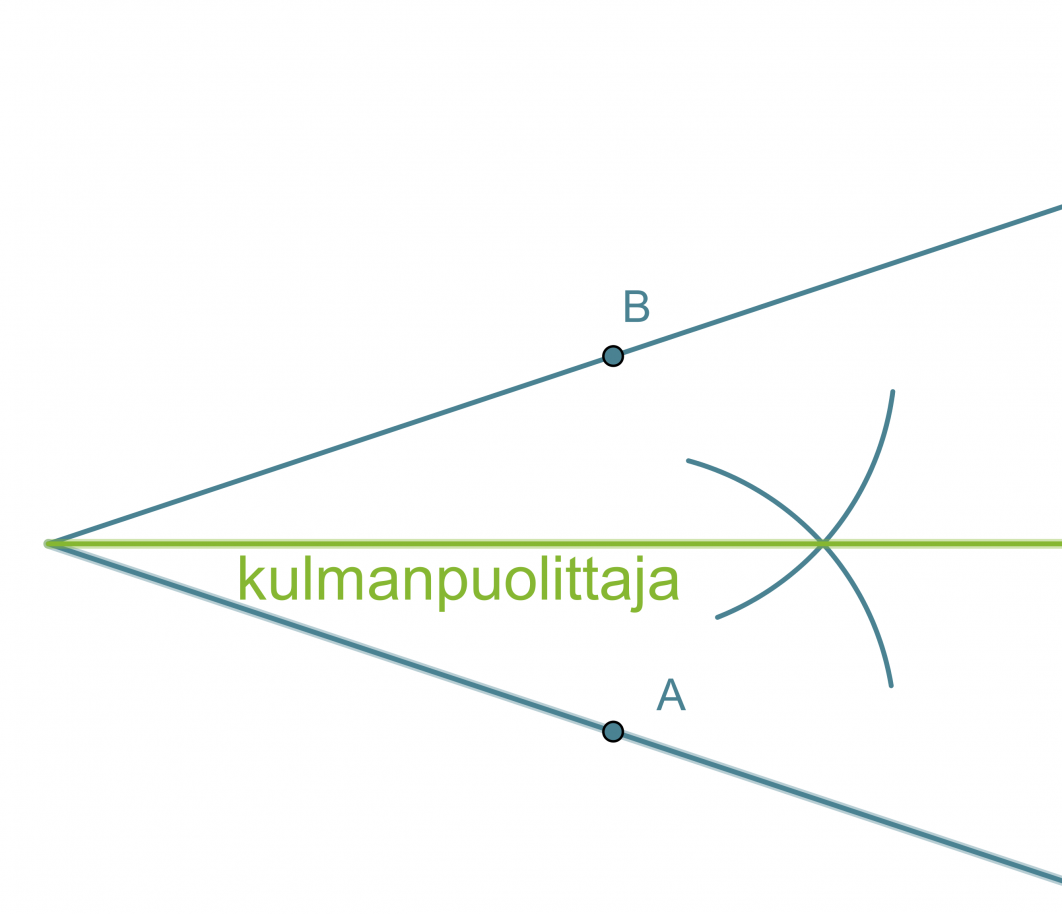
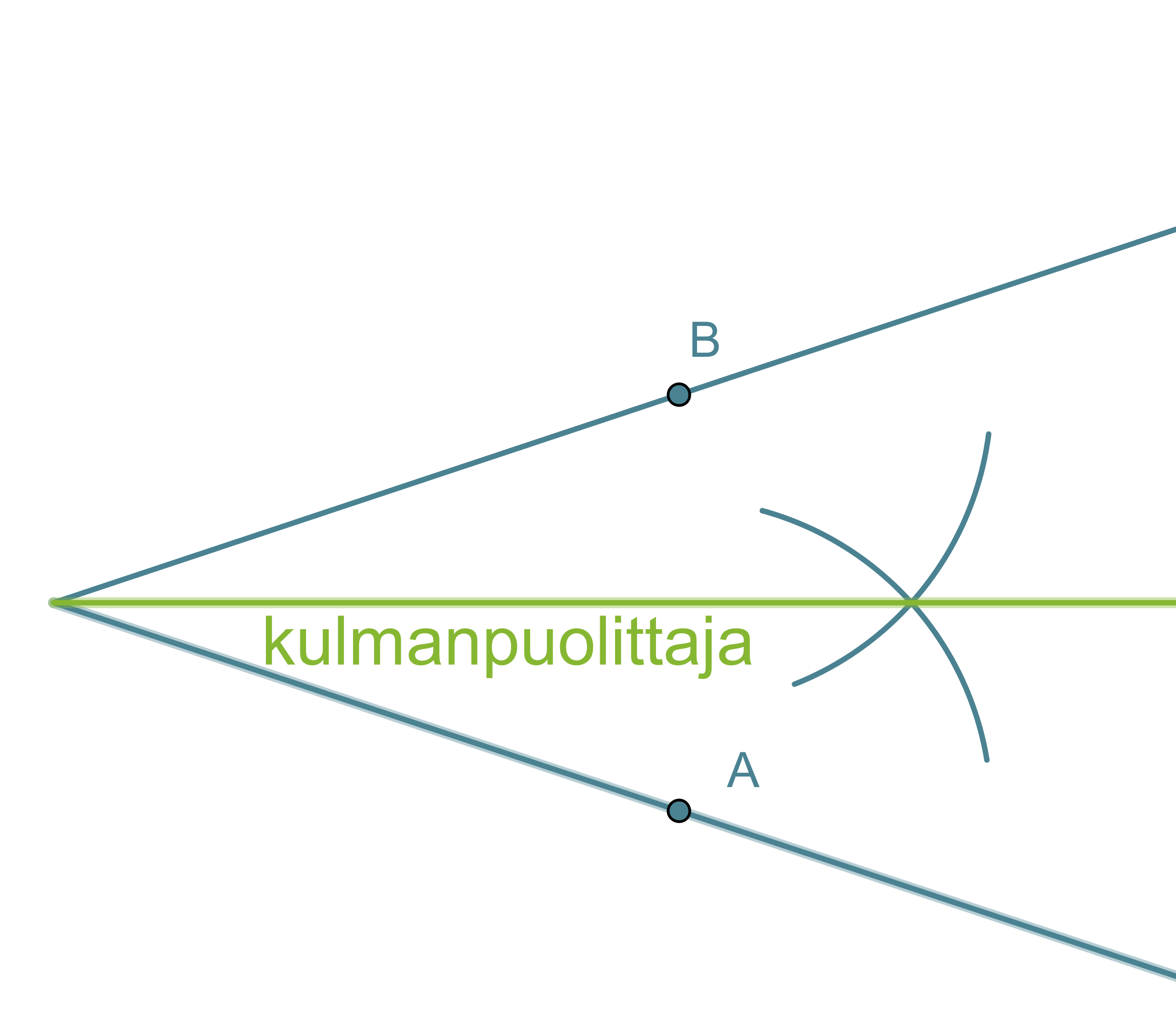
- Kulman kärki keskipisteenä piirretään ympyränkaari, joka leikkaa kulman molempia kylkiä.
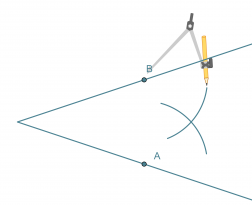
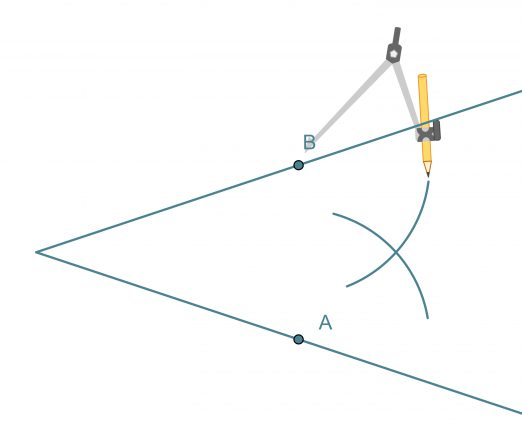
- Leikkauspisteet A ja B keskipisteinä piirretään samansäteiset ympyränkaaret siten, että ne leikkaavat toisensa kulman aukeamassa.
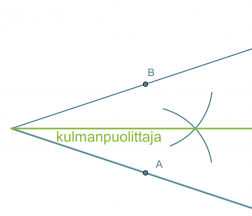
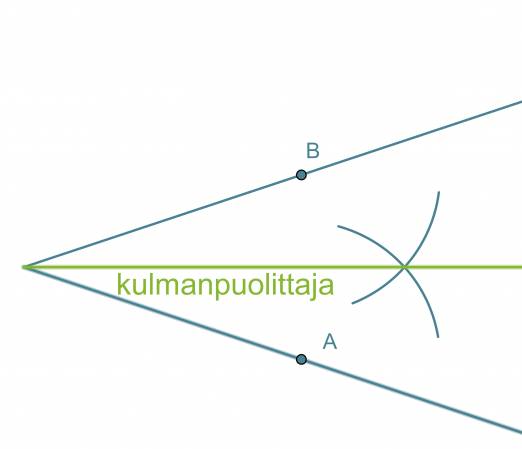
- Ympyränkaarien leikkauspiste yhdistetään kulman kärkipisteeseen. Tämä puolisuora on kulmanpuolittaja.
Kolmion piirtäminen
Piirretään kolmio ABC, jonka sivujen pituudet ovat 6 cm, 5 cm ja 4 cm.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
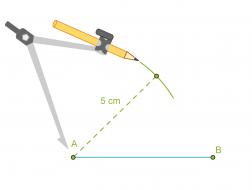
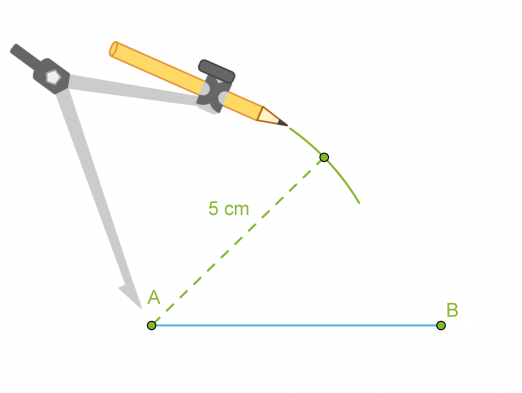
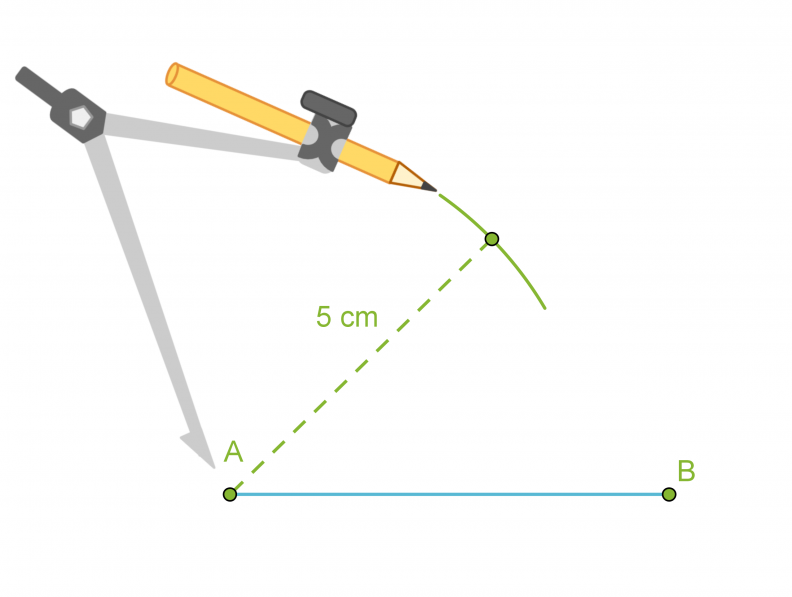
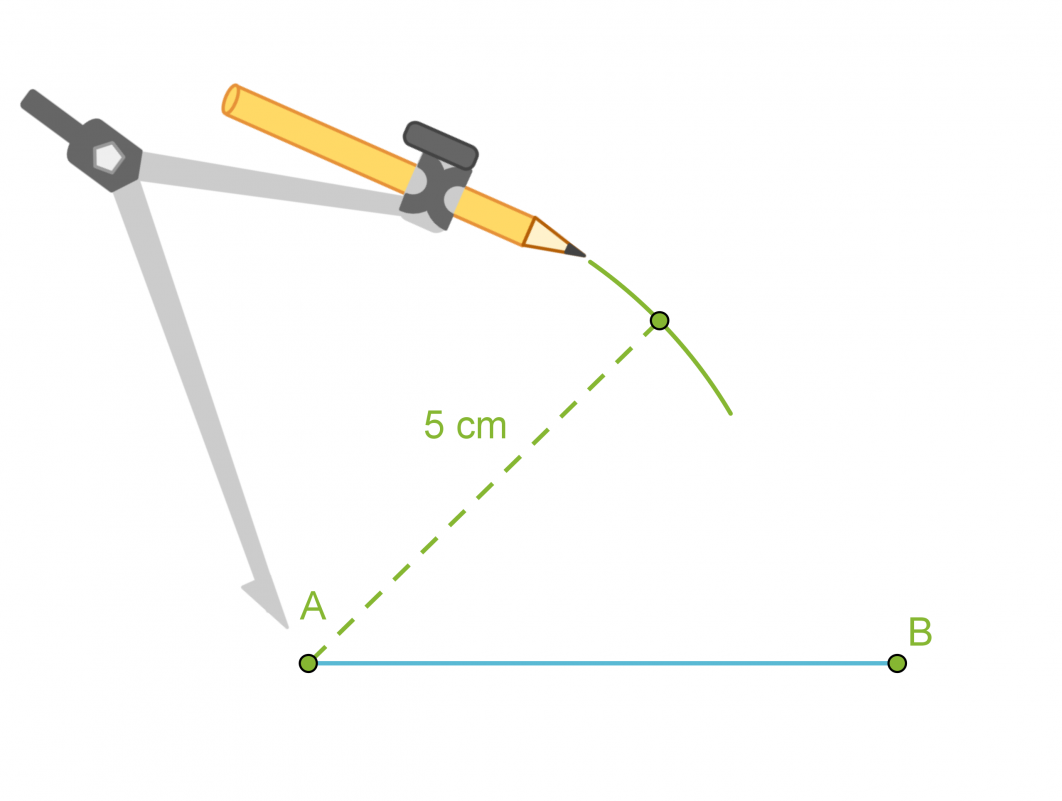
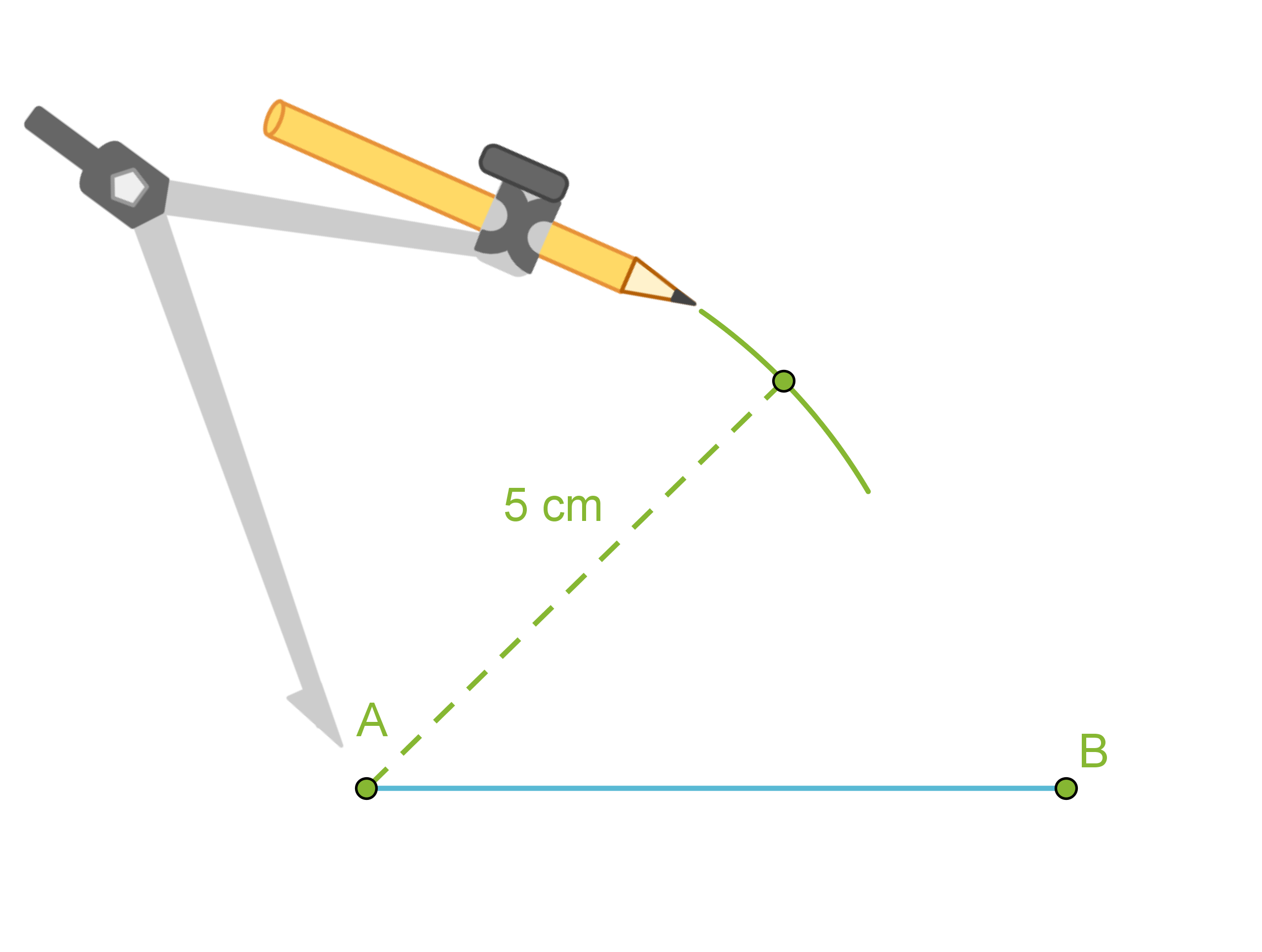
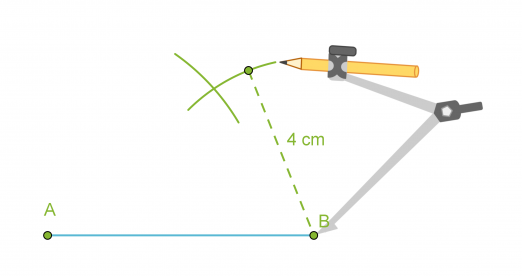
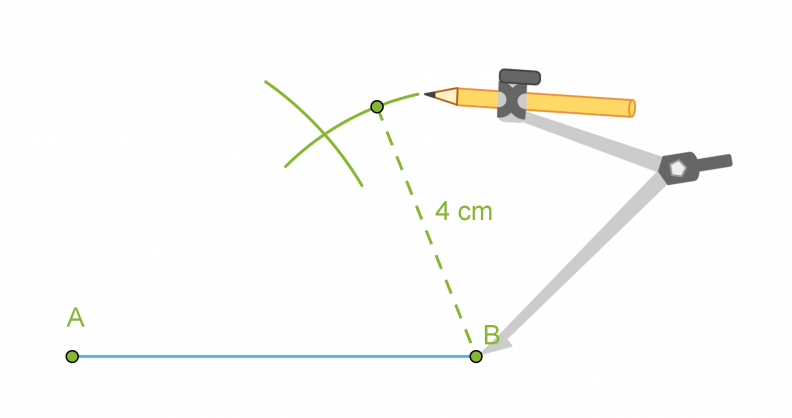
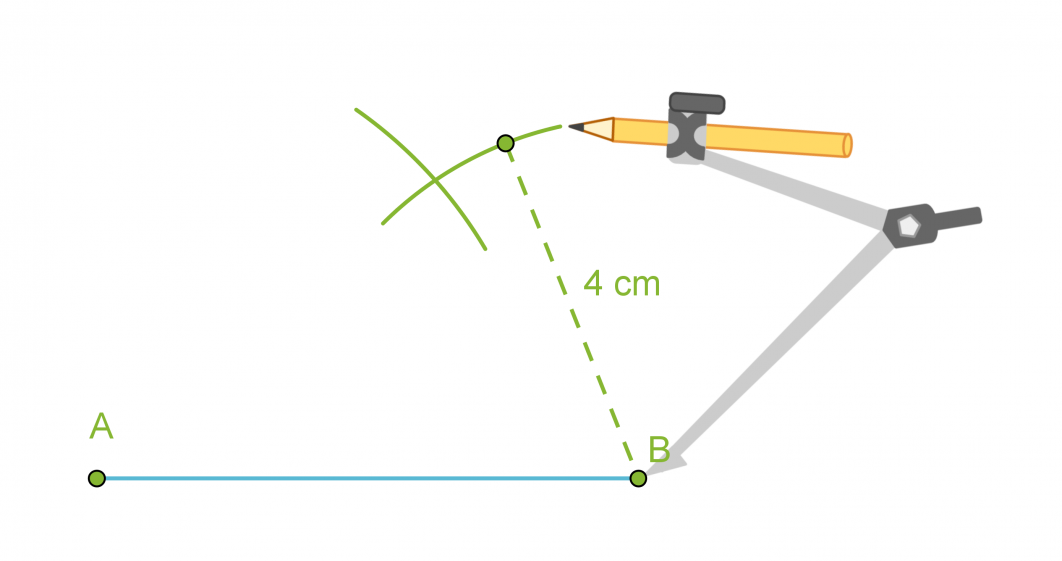
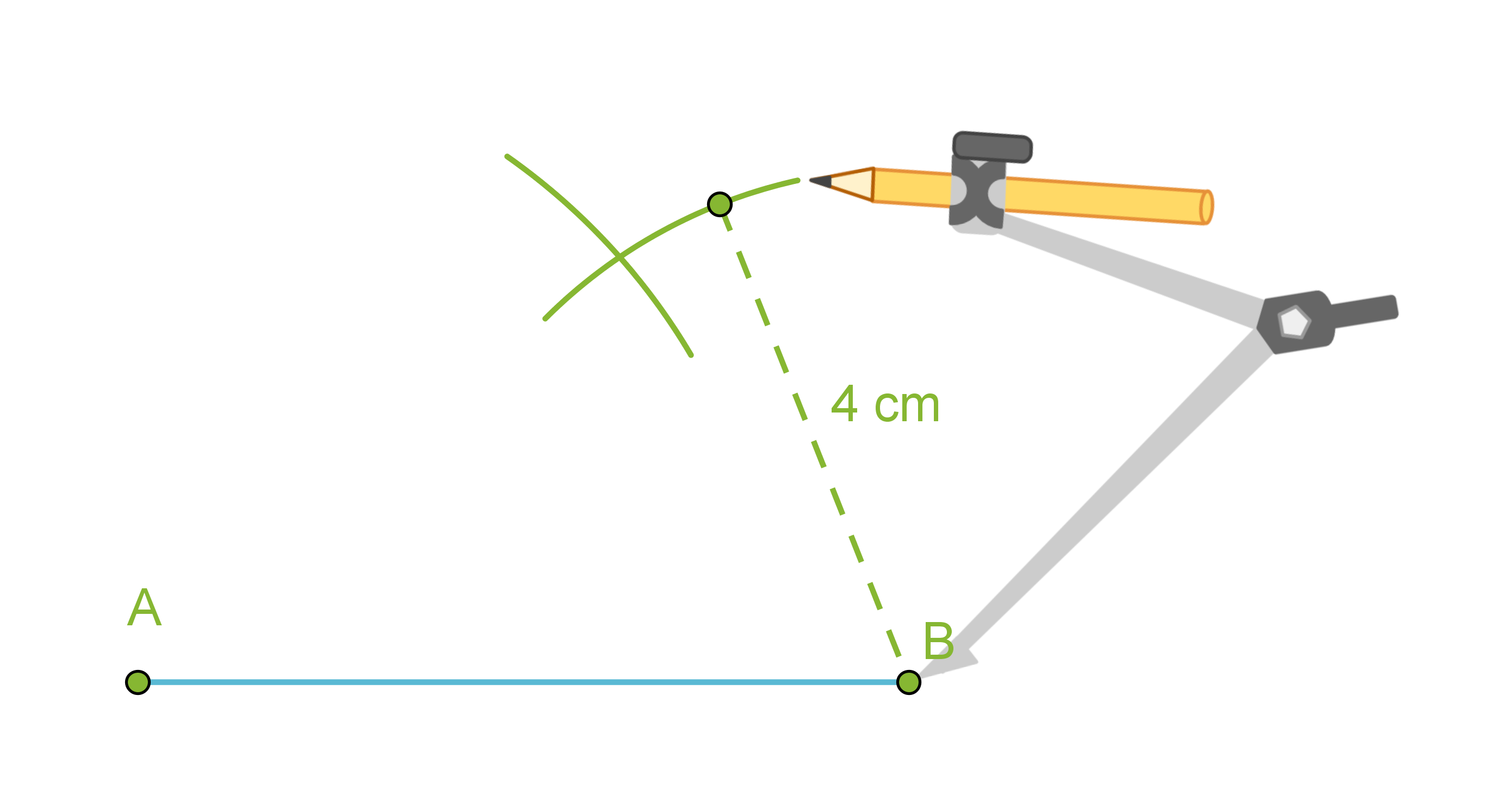
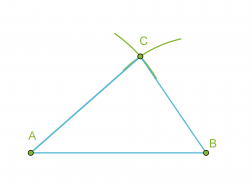
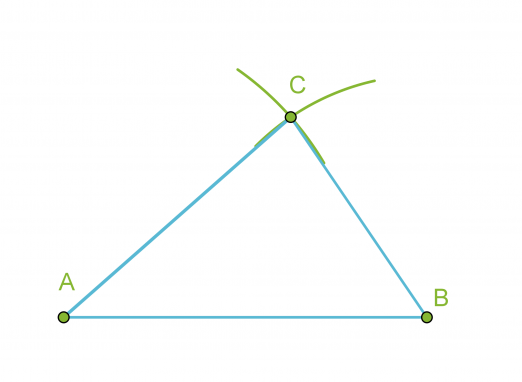
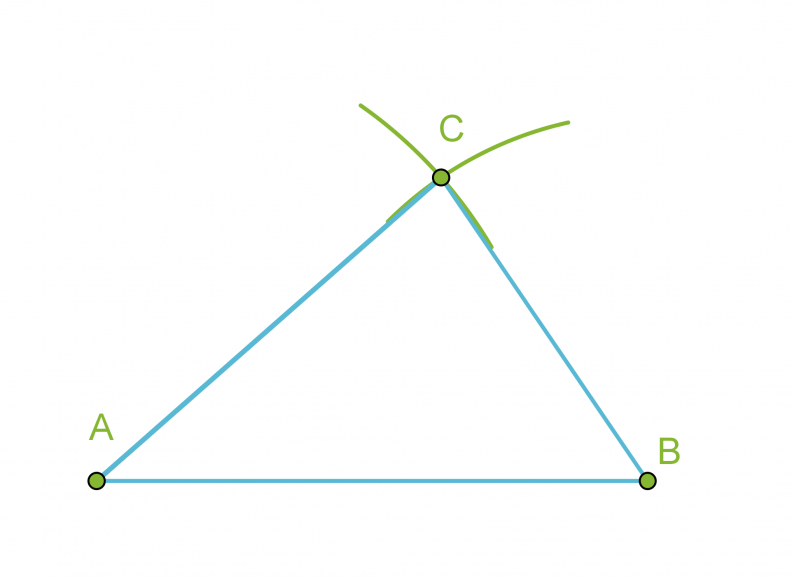
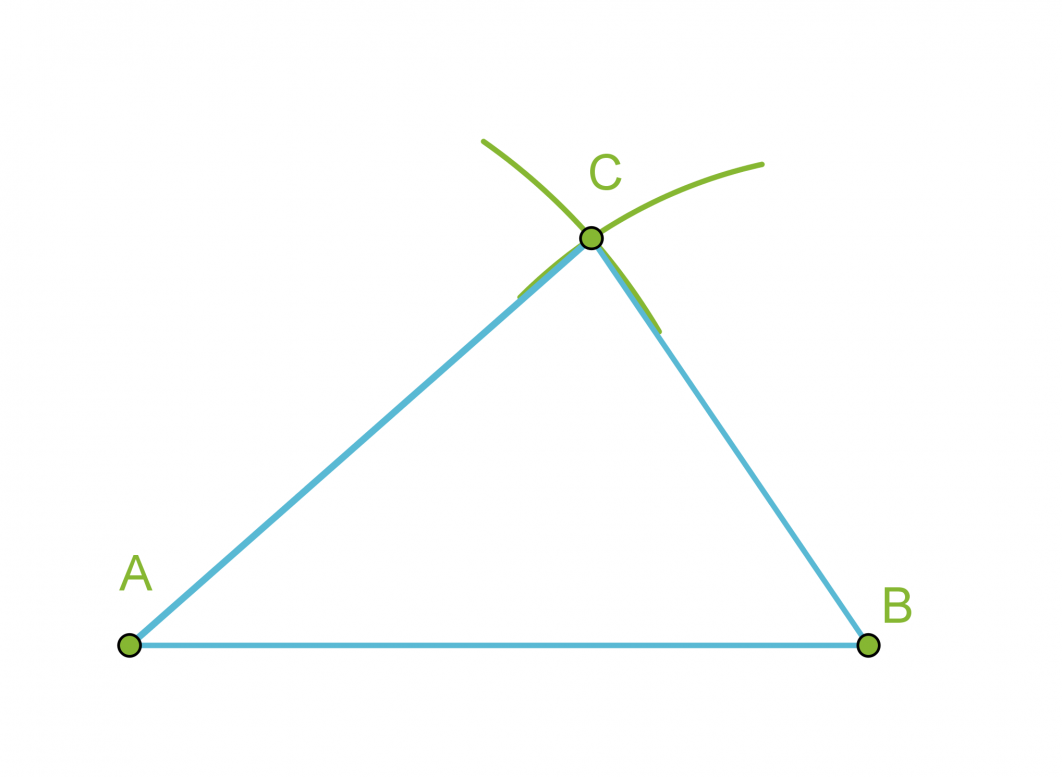
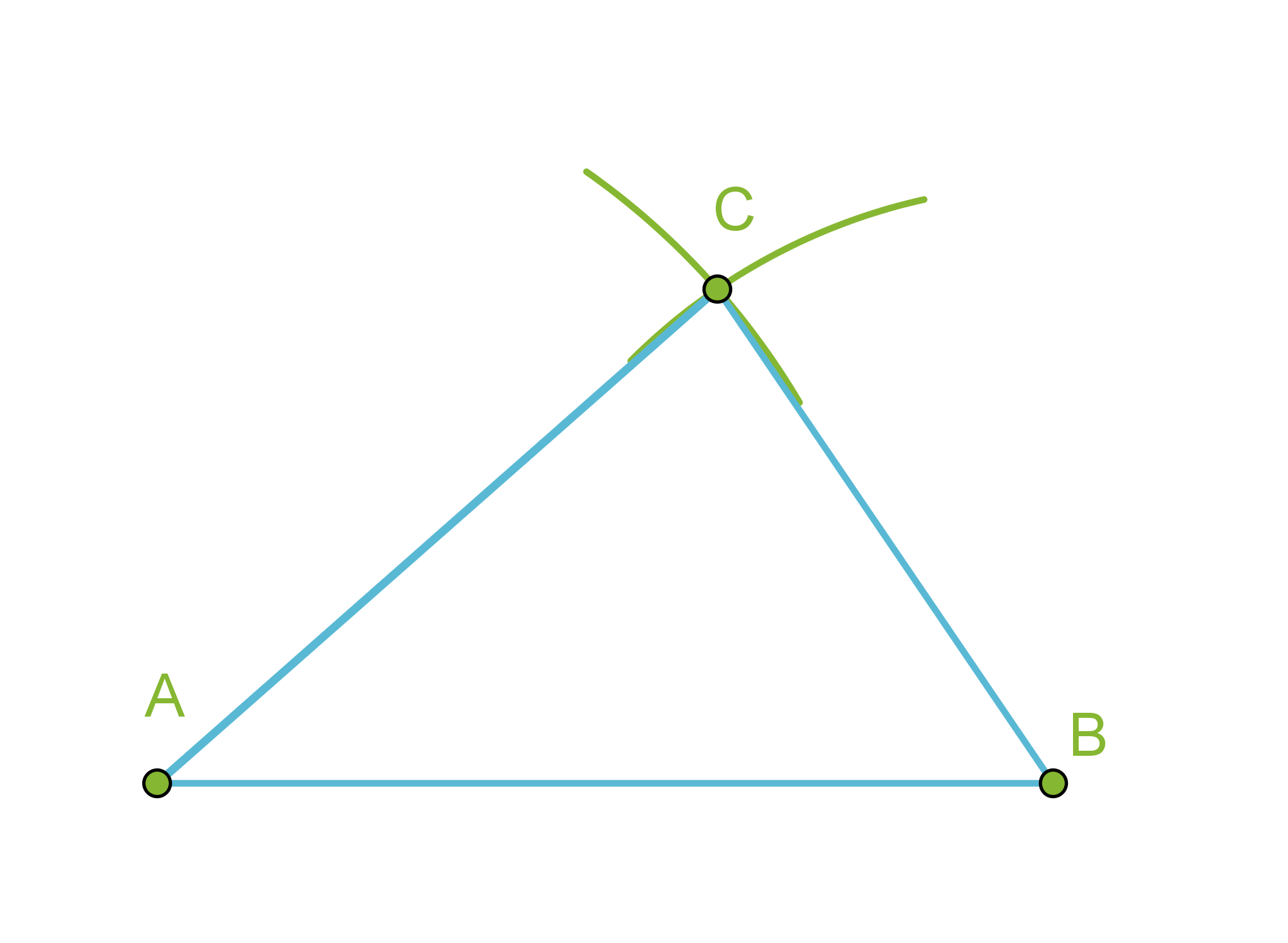
- Piirretään kolmion yksi sivu eli jana AB.
- Käytetään kolmion sivuksi valitun janan päätepisteitä A ja B ympyränkaarien keskipisteinä ja piirretään kaksi ympyränkaarta niillä säteillä, jotka ovat kolmion sivujen pituudet.
- Yhdistetään ympyränkaarien leikkauspiste C janan AB päätepisteisiin.
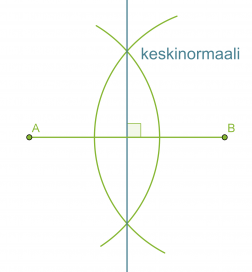
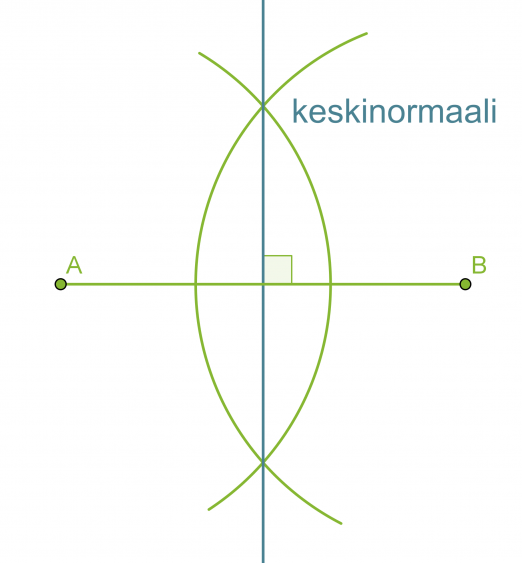
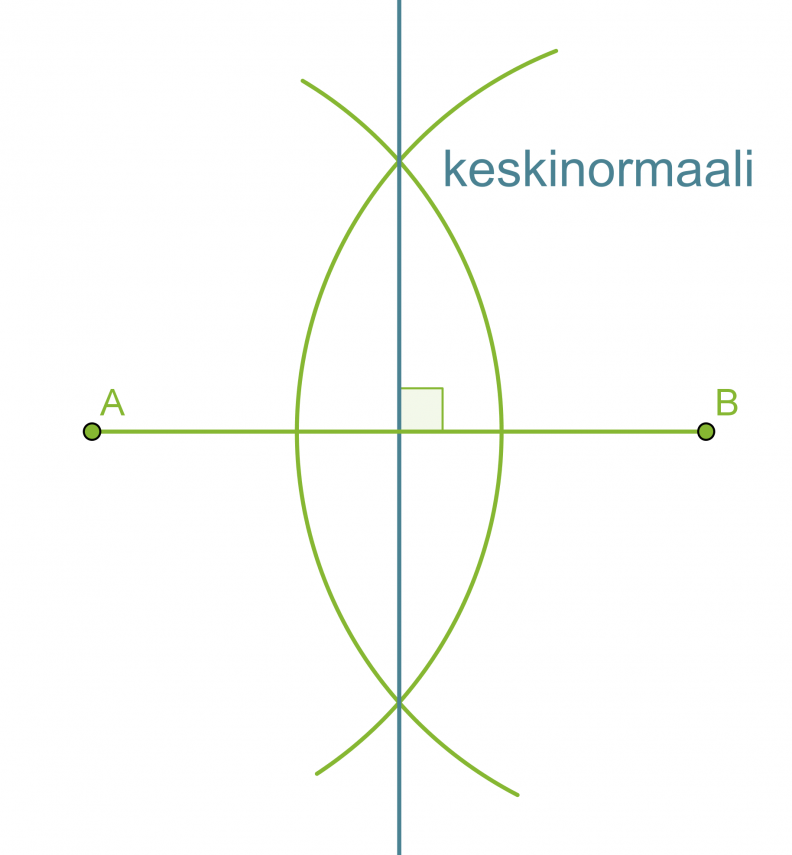
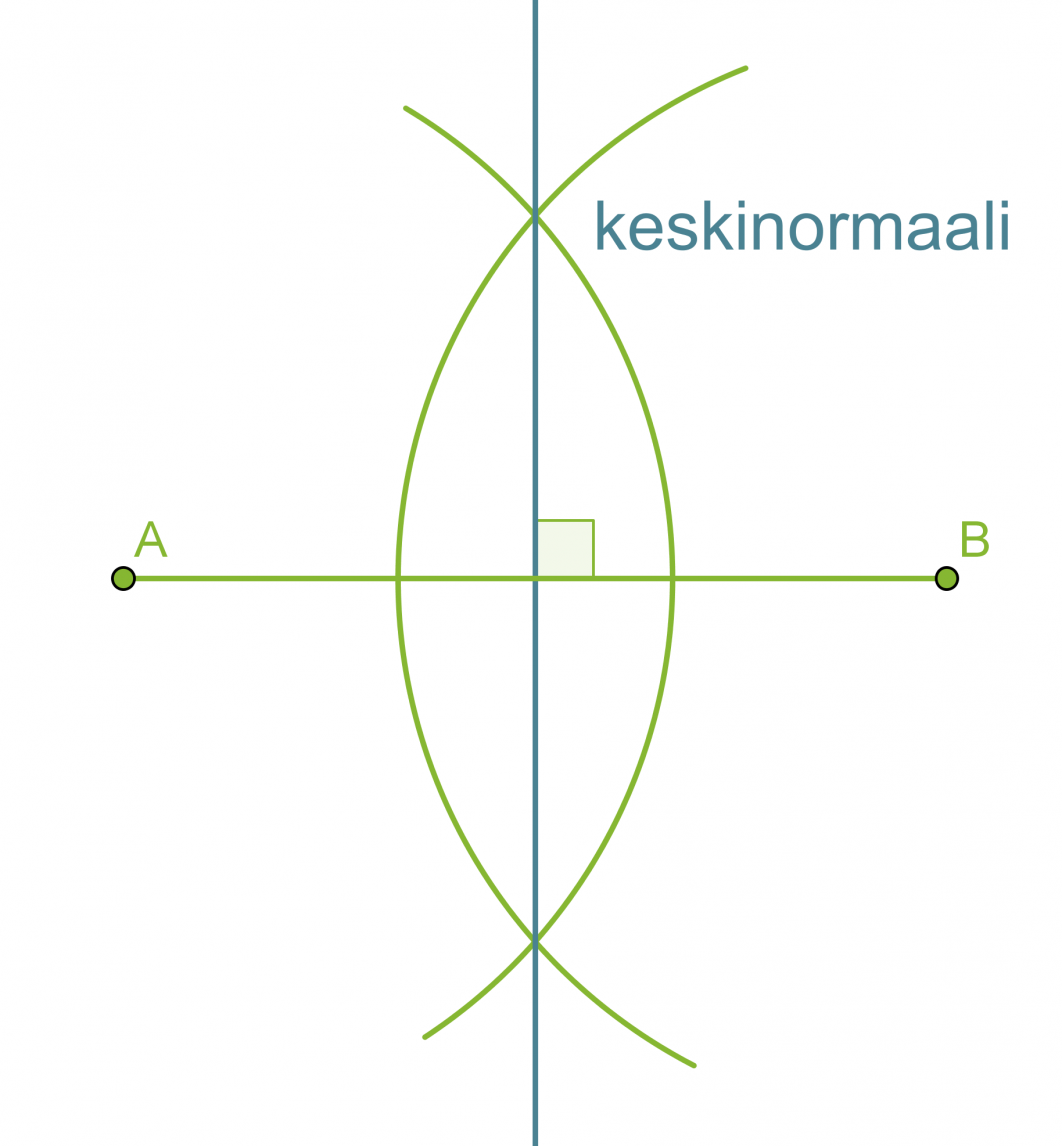
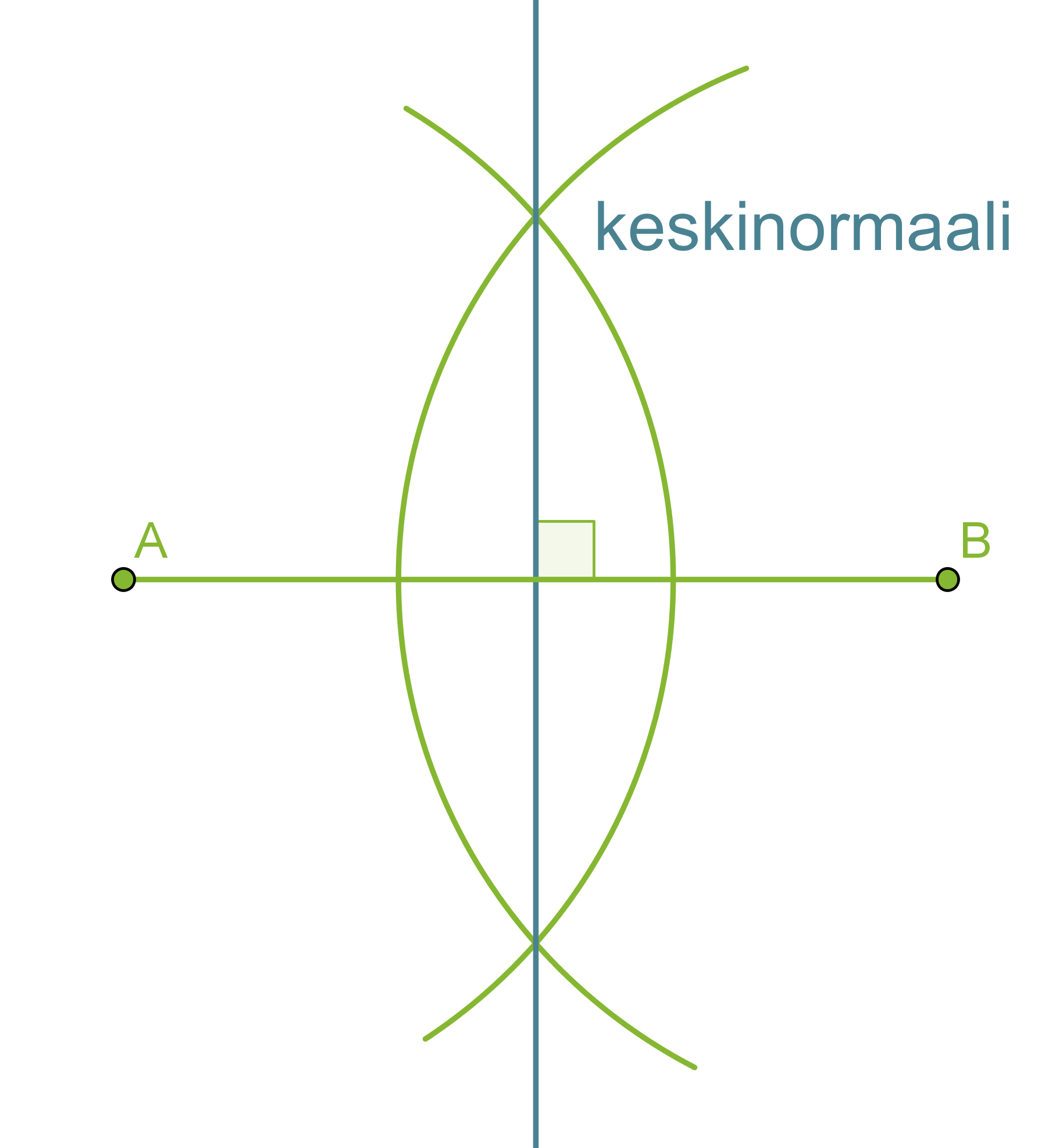
Janan keskinormaalin piirtäminen
Useissa geometrisissa piirtämistehtävissä käytetään janan keskinormaalia mittaamiseen, sillä jokainen keskinormaalin piste on yhtä kaukana janan päätepisteistä.
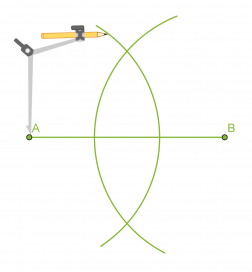
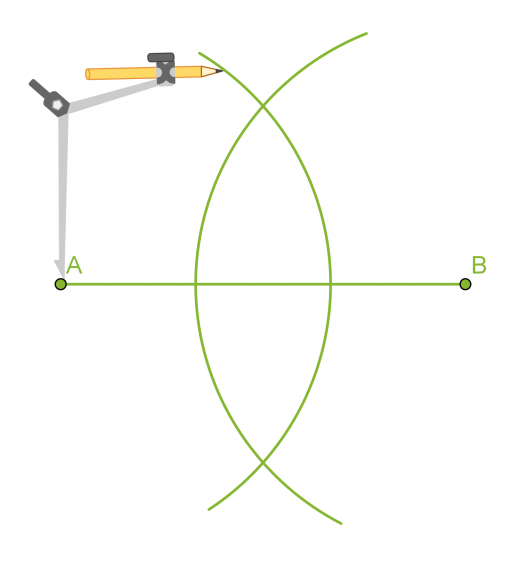
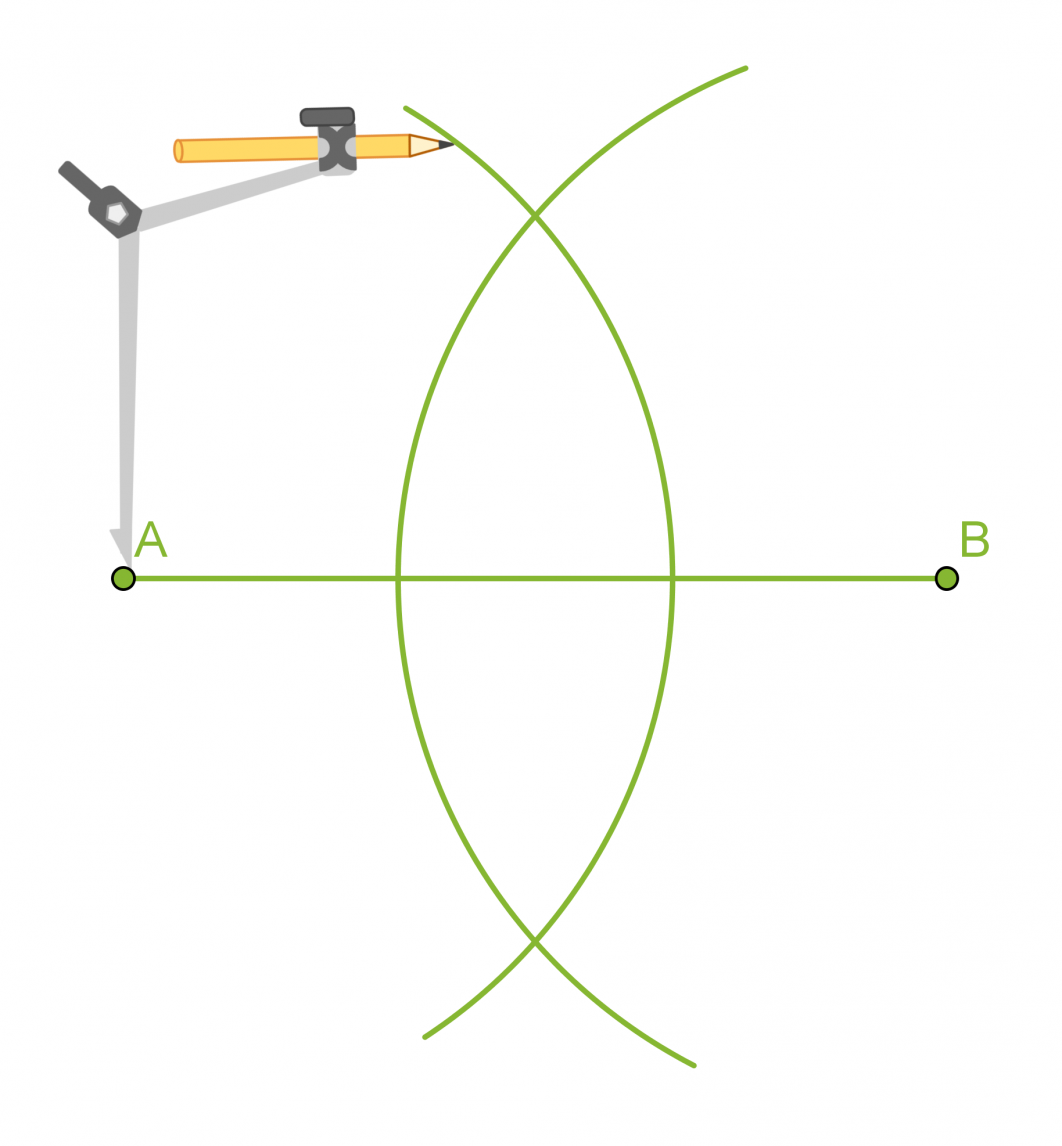
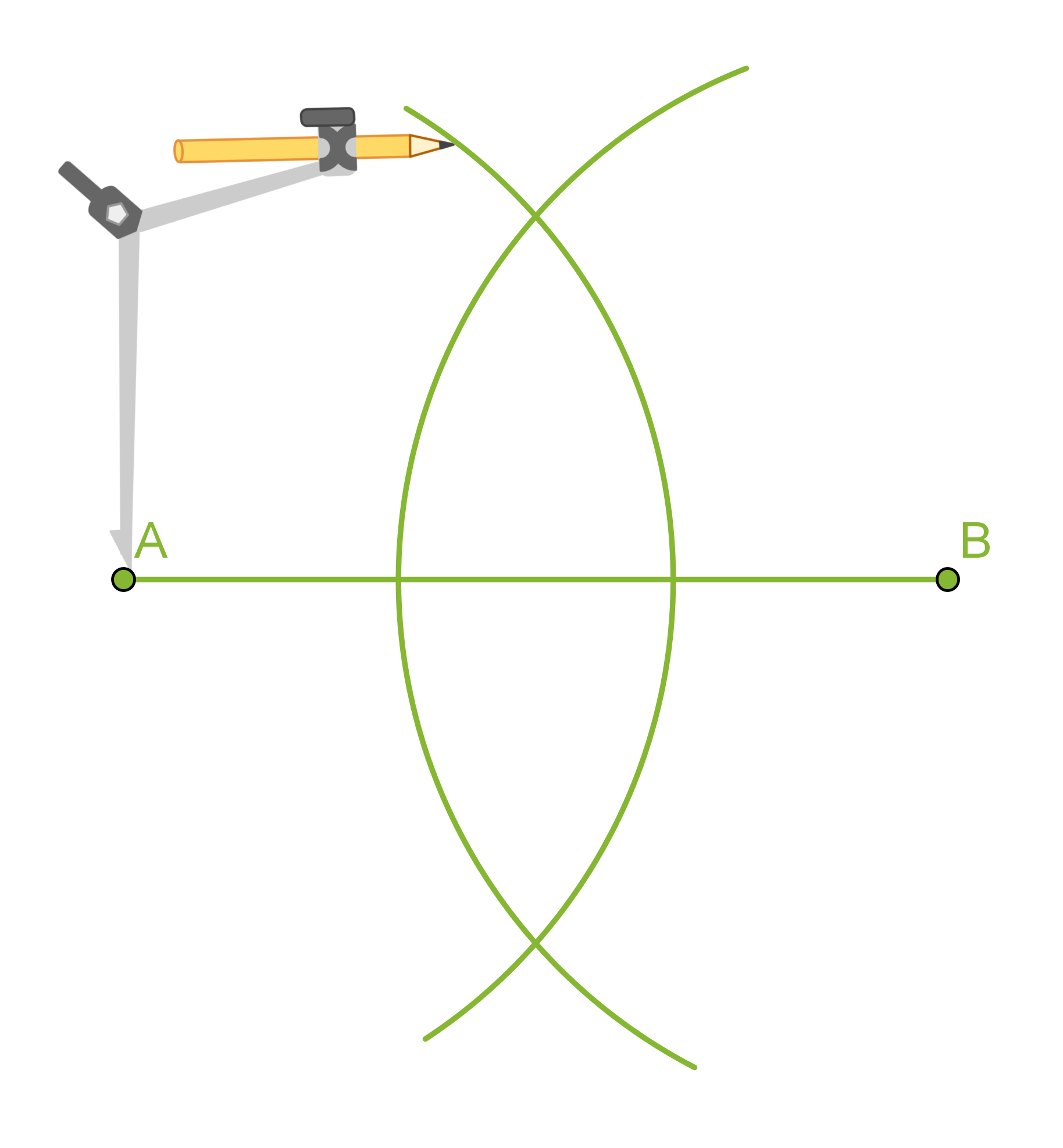
Piirretään annetulle janalle AB keskinormaali.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Suoralle piirretään geometrisesti normaali siten, että ensiksi piirretään jokin suoran piste keskipisteenä ympyrä. Syntyviä suoran ja ympyräkaaren leikkauspisteitä käsitellään samoin kuin edellä pisteitä A ja B.
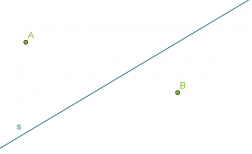
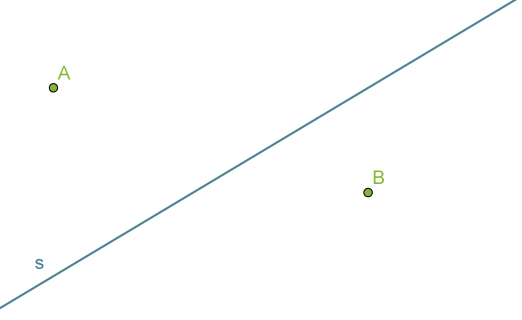
Esimerkki 1.
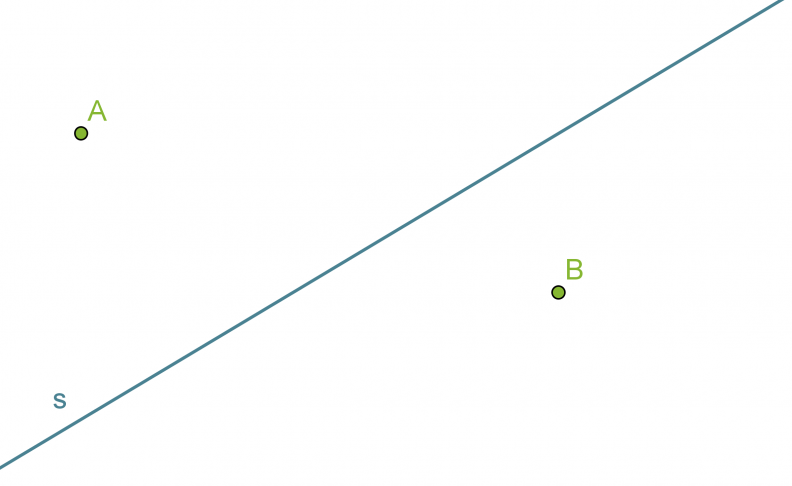
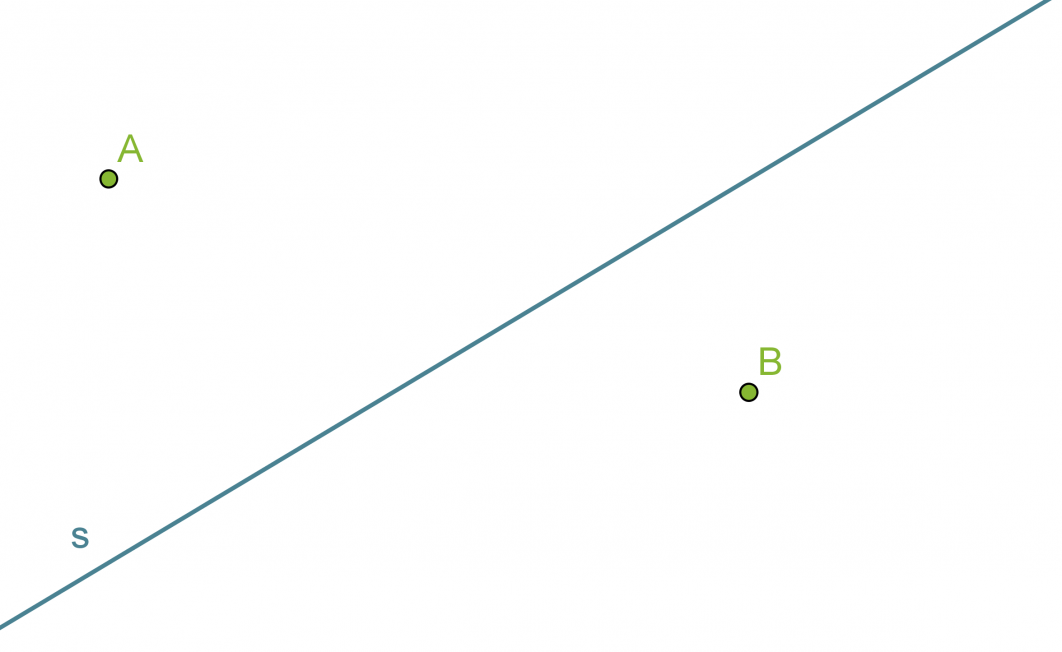
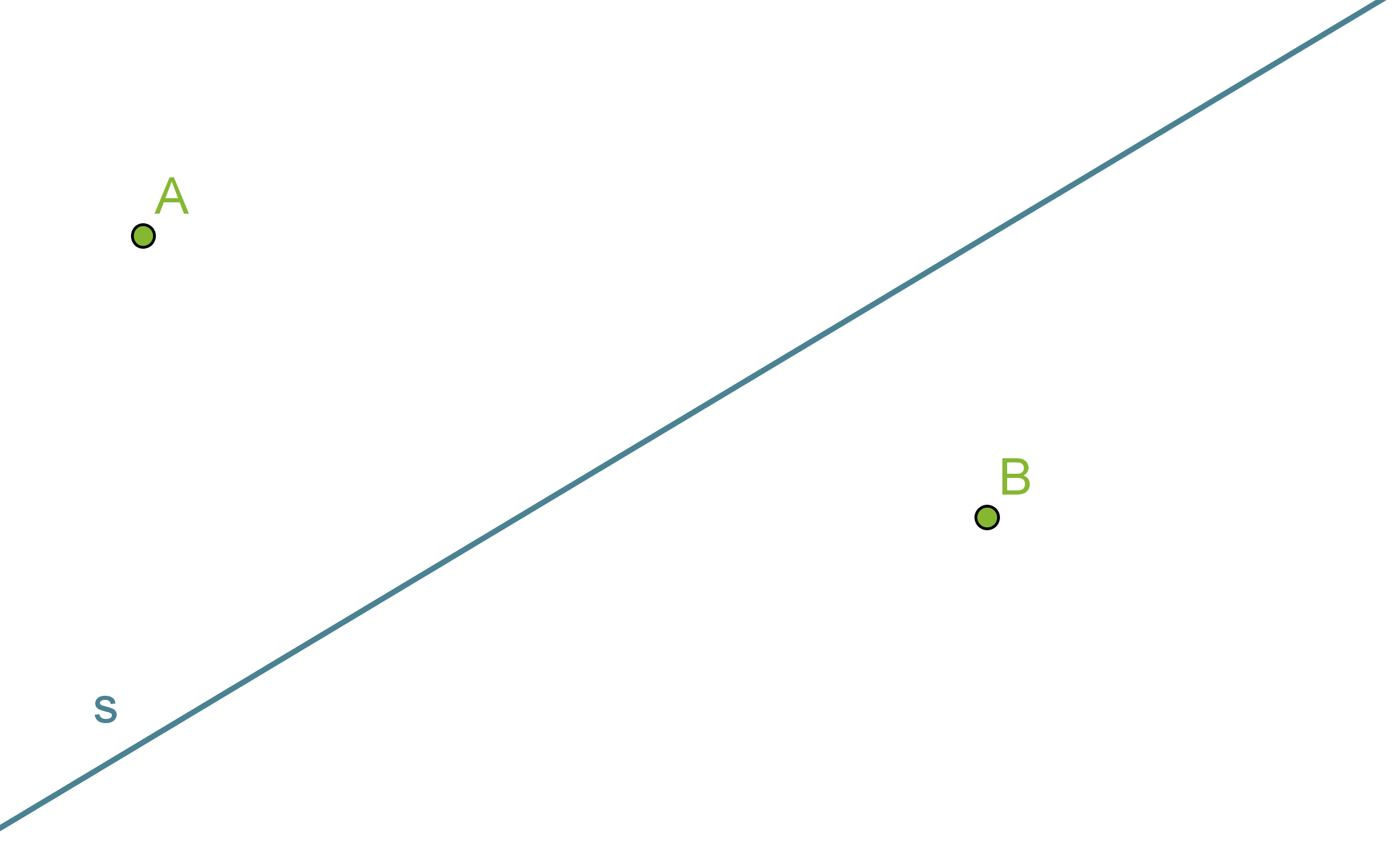
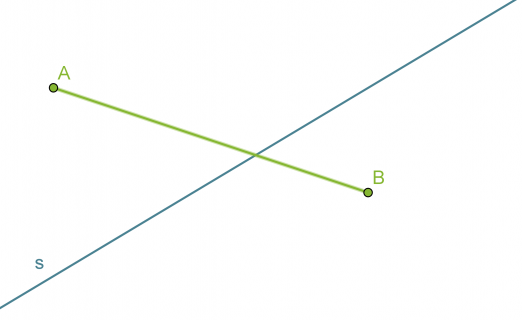
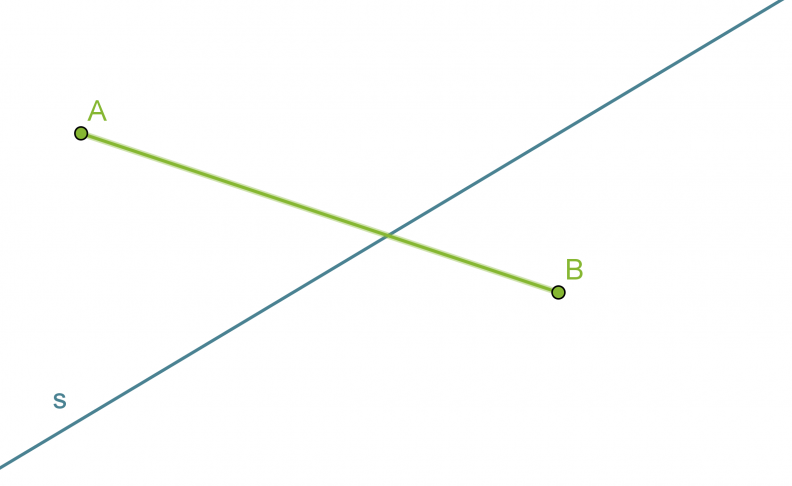
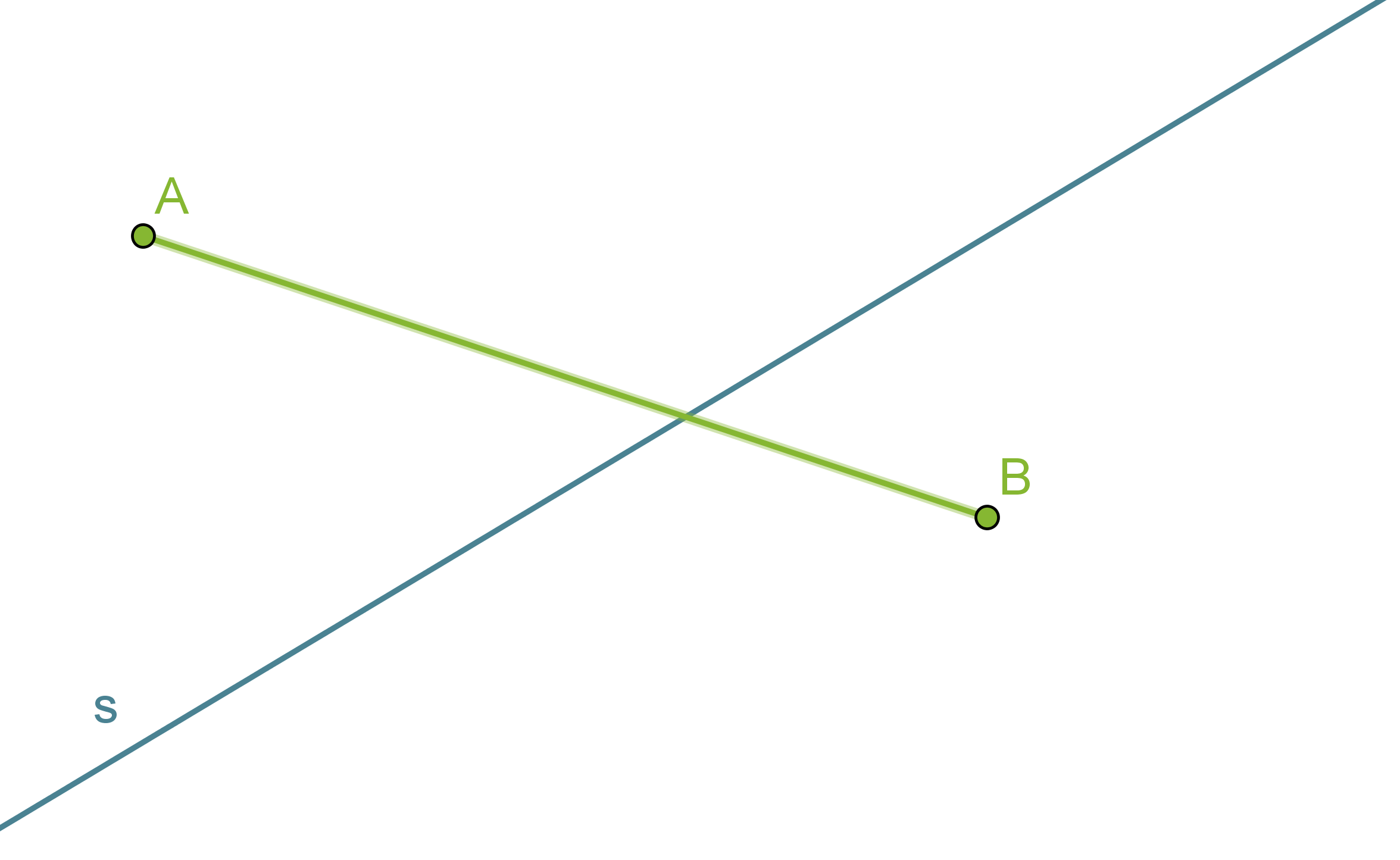
Etsitään suoralta s sellainen piste, joka on yhtä kaukana pisteistä A ja B.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
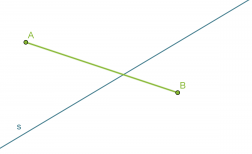
Yhdistetään pisteet A ja B janaksi.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
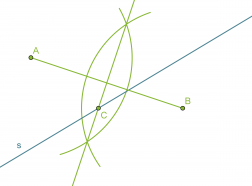
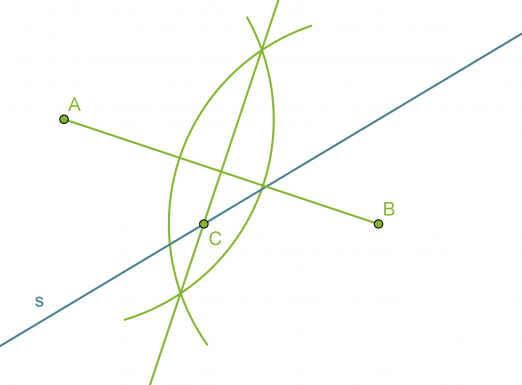
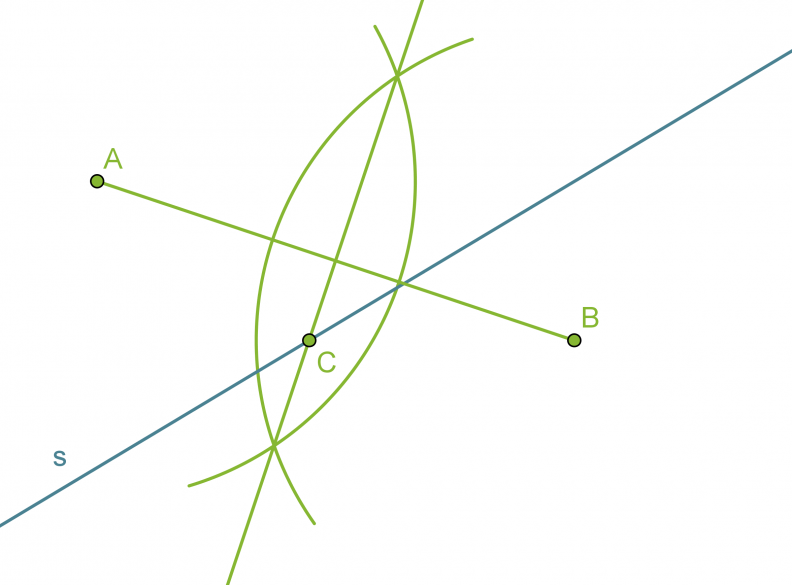
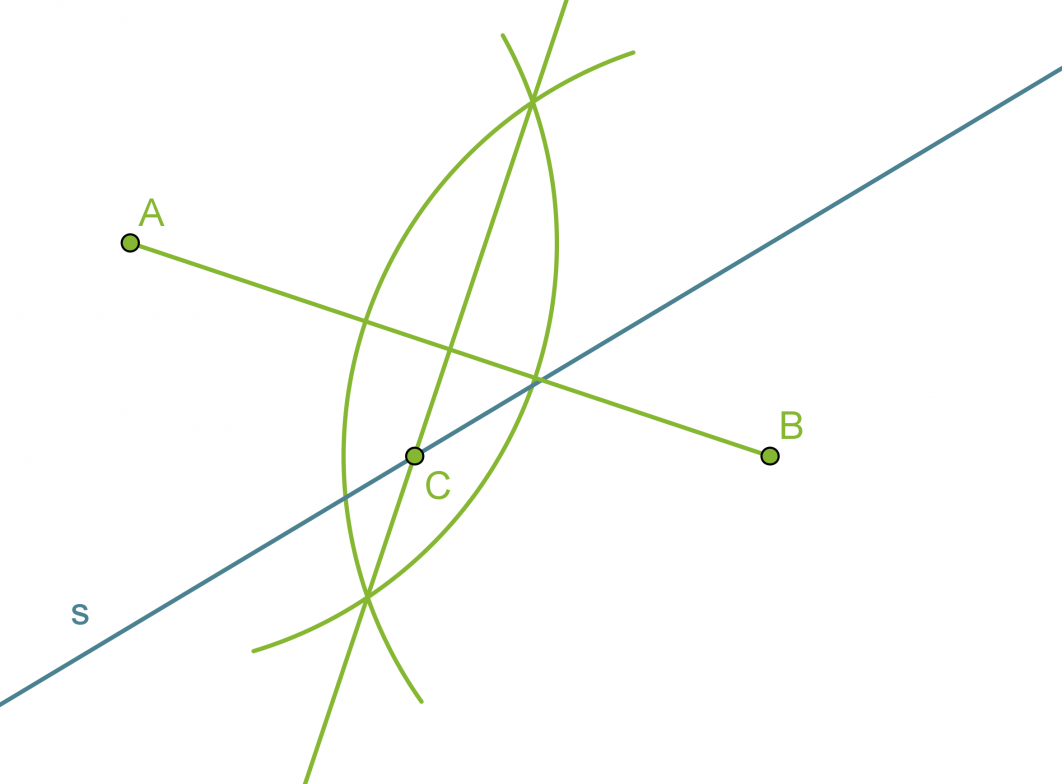
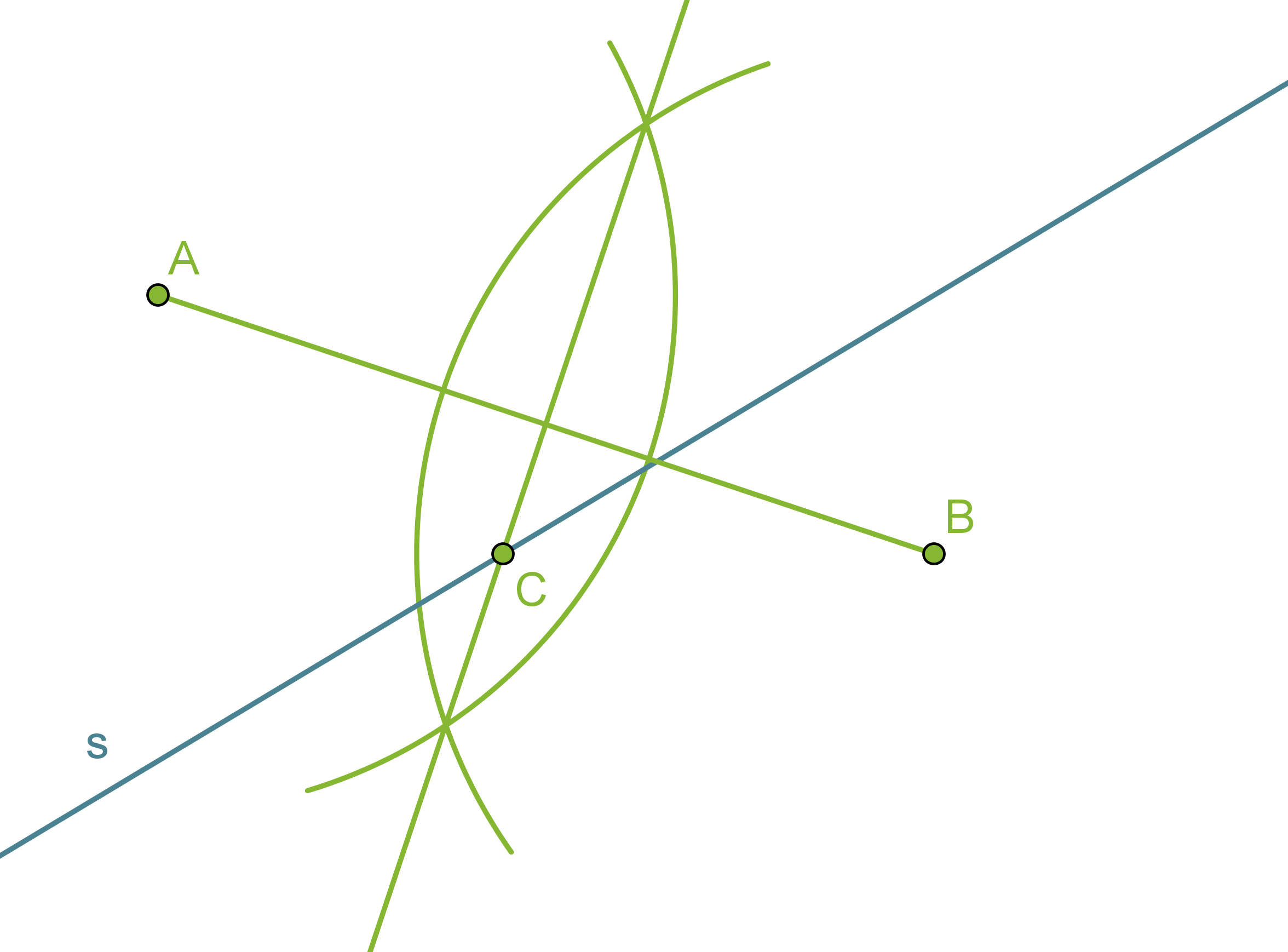
Piirretään janalle AB keskinormaali.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suoran s ja janan AB keskinormaalin leikkauspiste C on vaadittu piste.
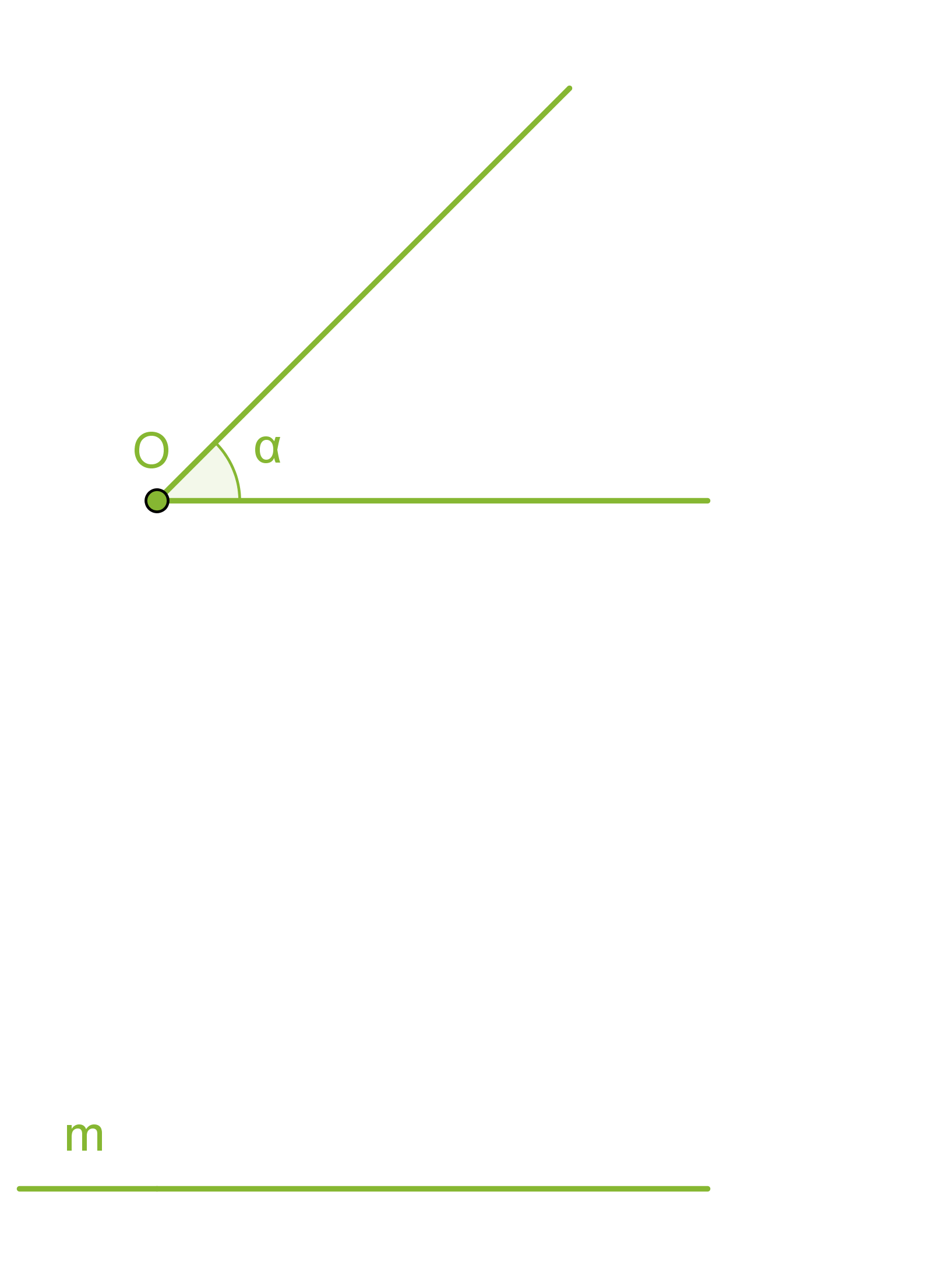
Kulman siirtäminen
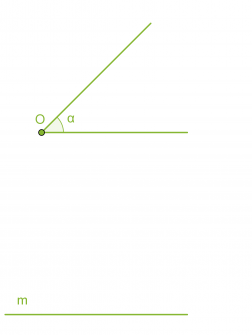
Klikkaa kuva suuremmaksi!
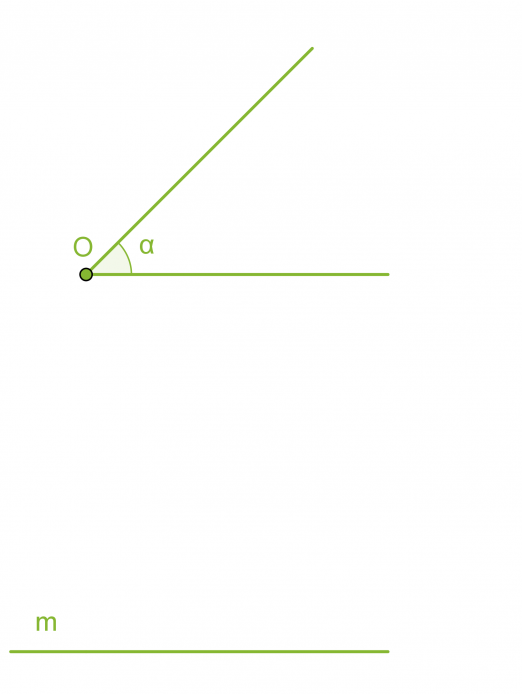
Klikkaa kuva suuremmaksi!
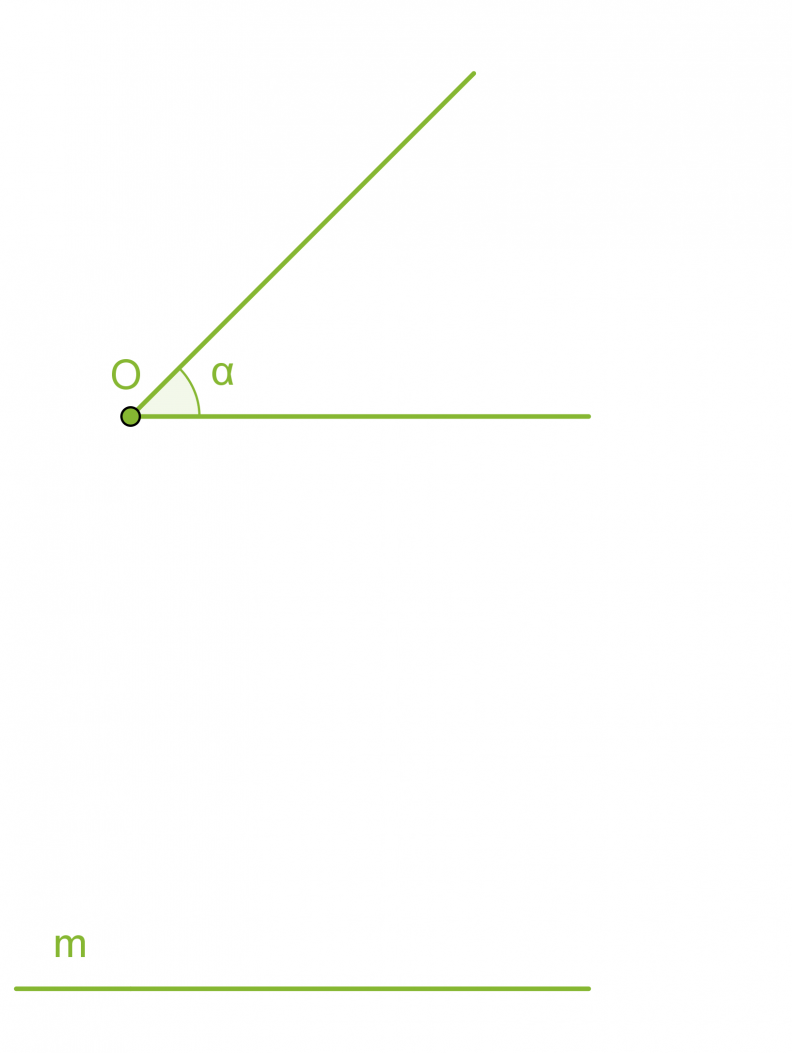
Klikkaa kuva suuremmaksi!
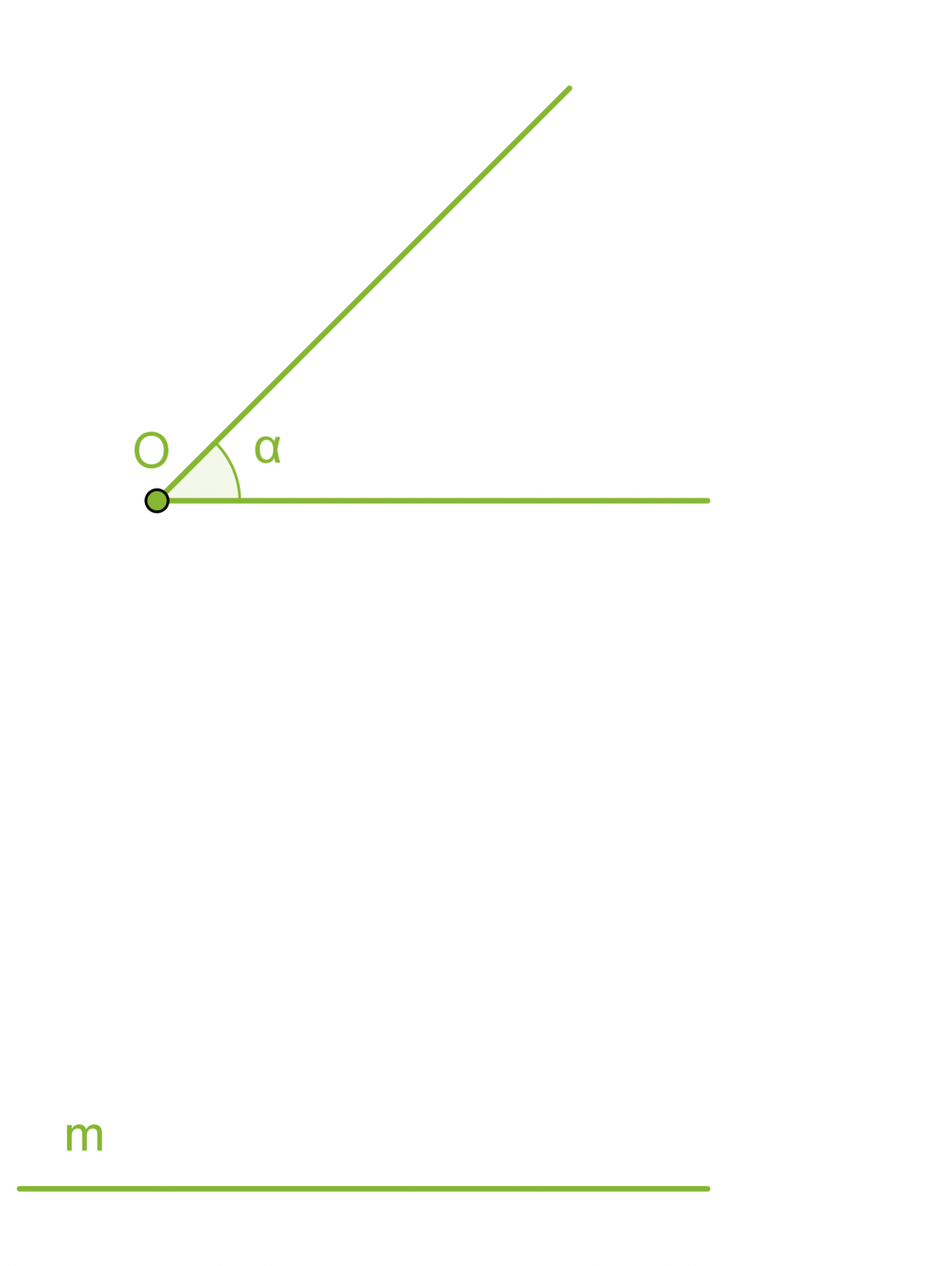
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
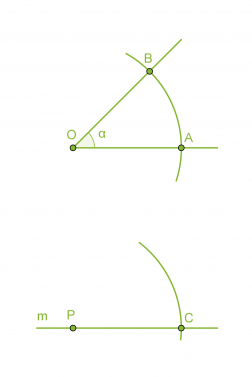
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
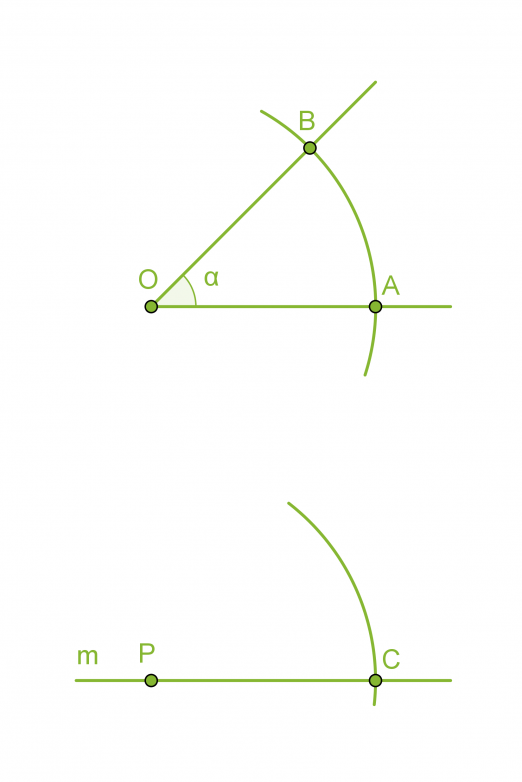
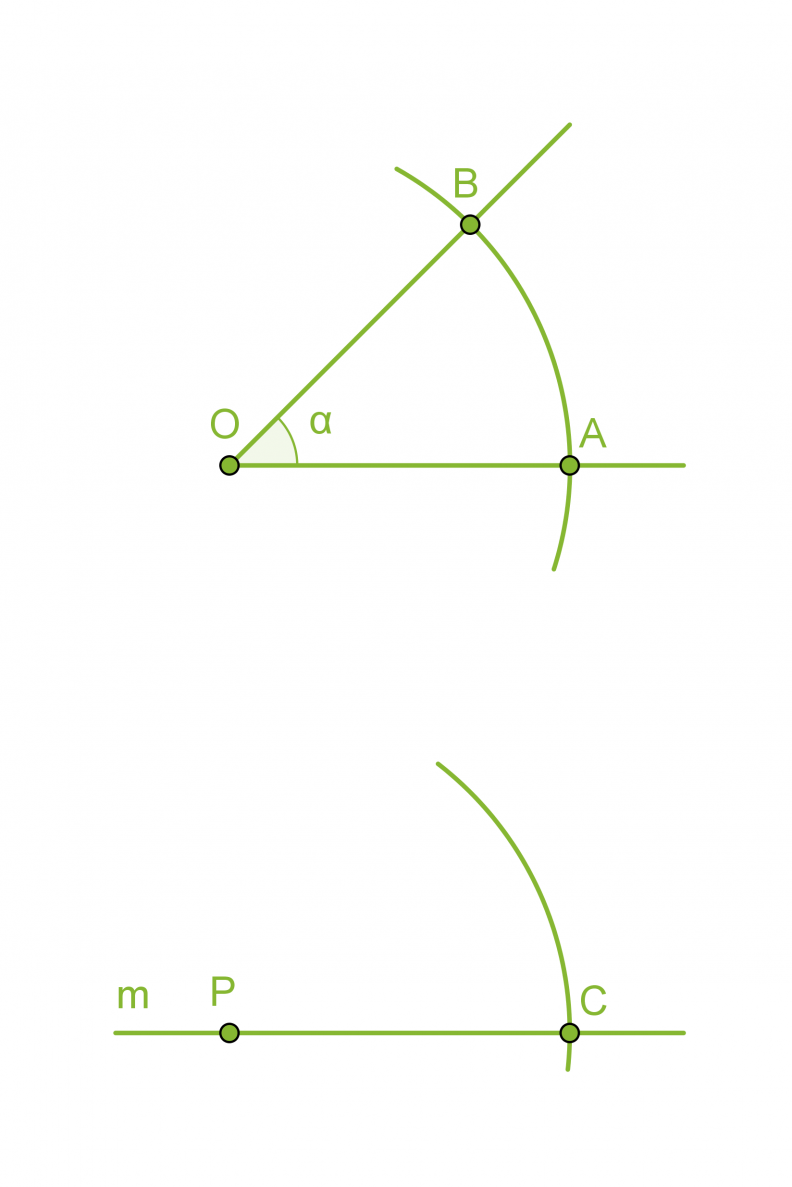
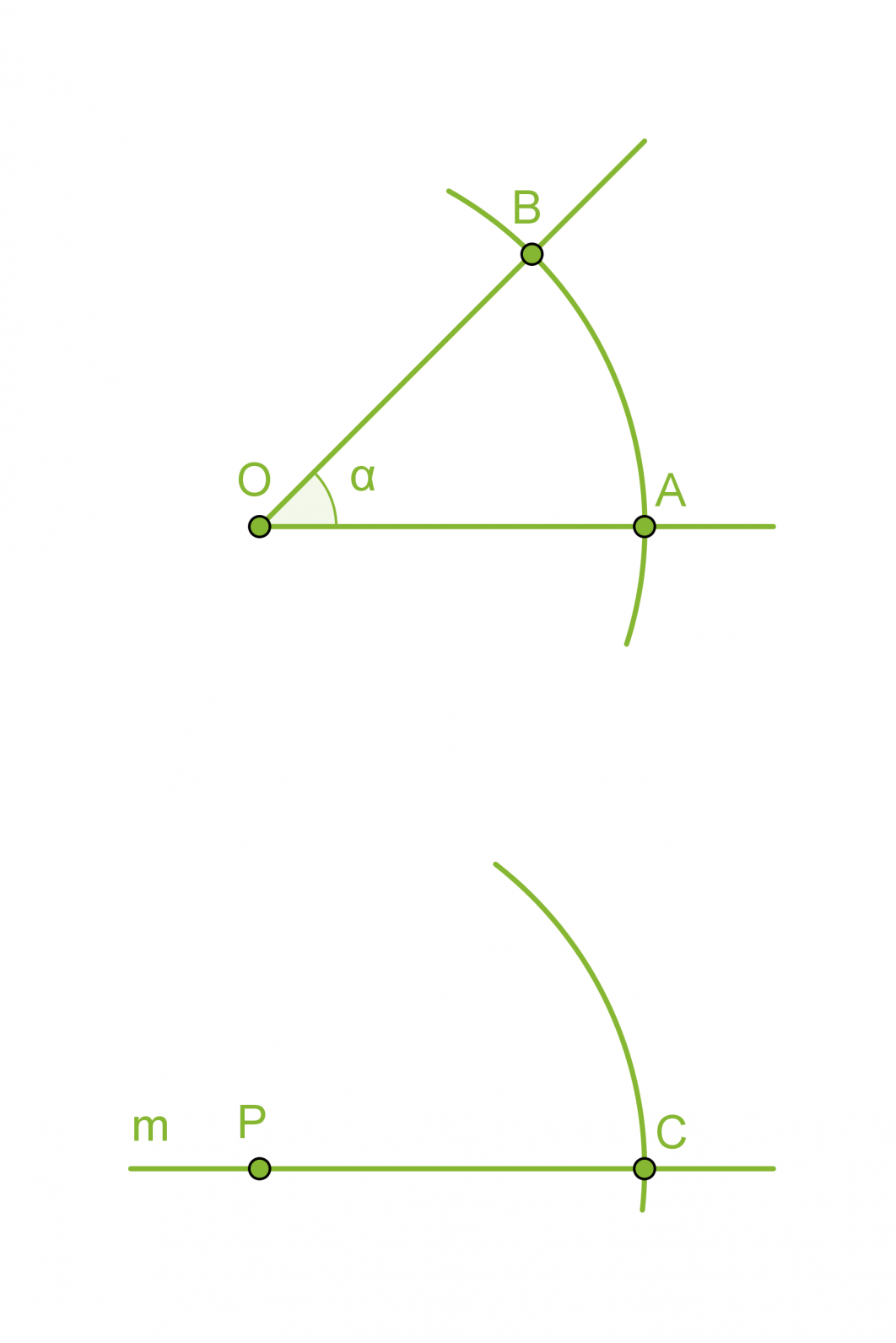
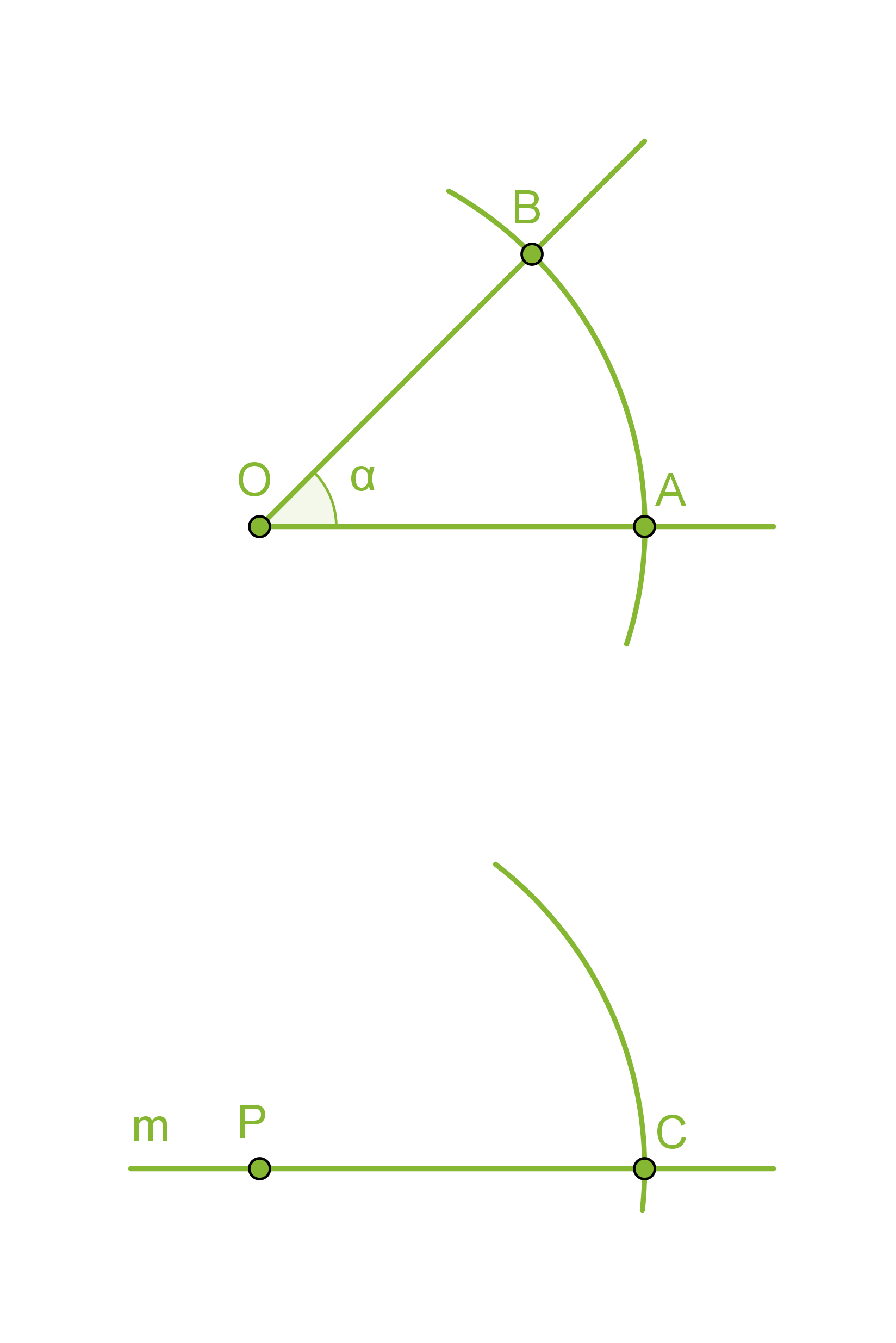
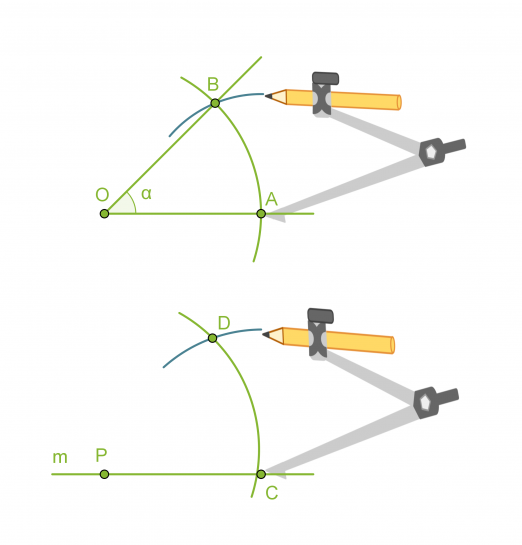
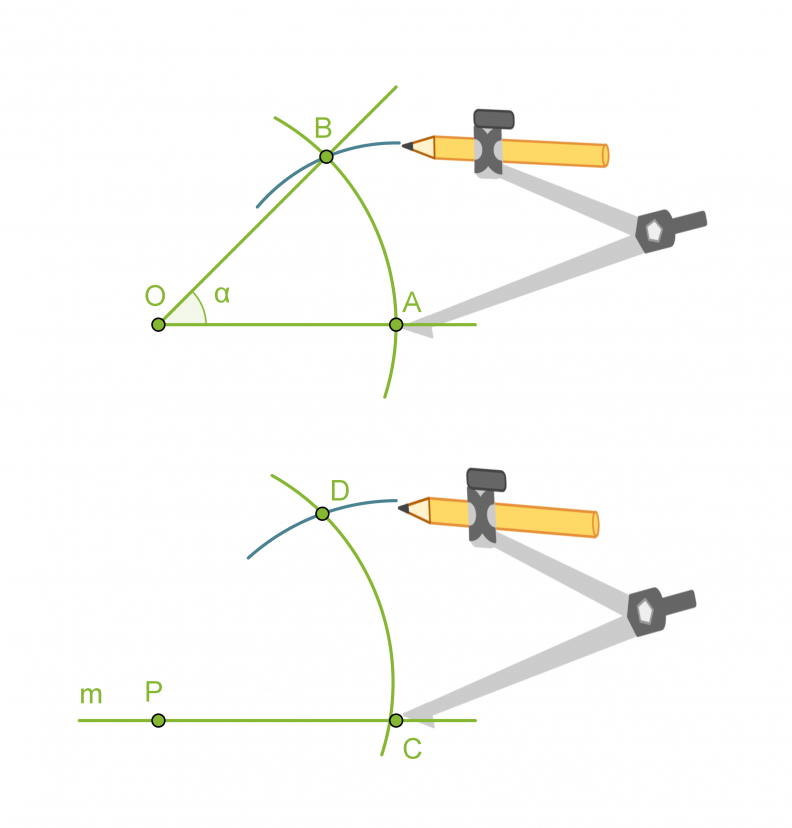
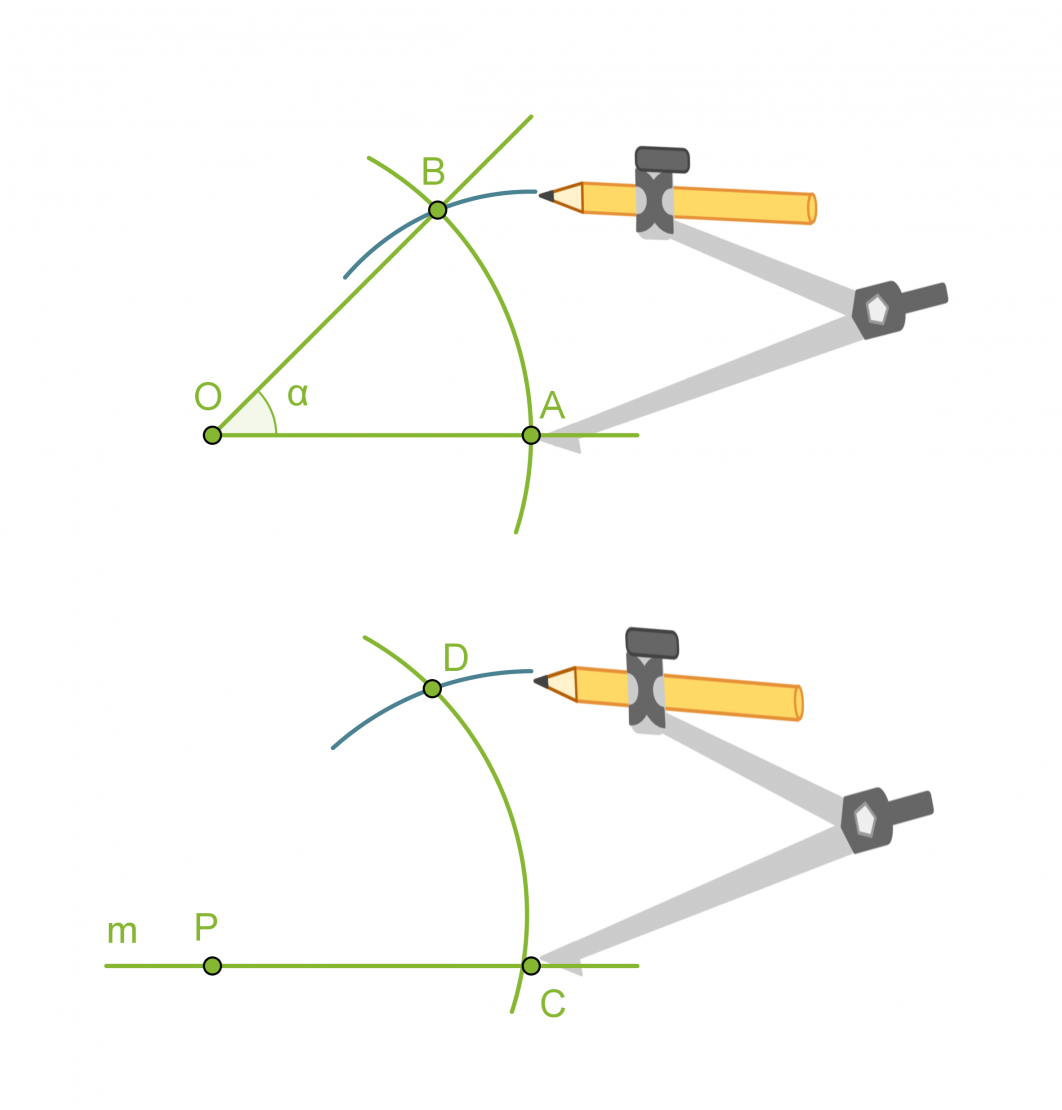
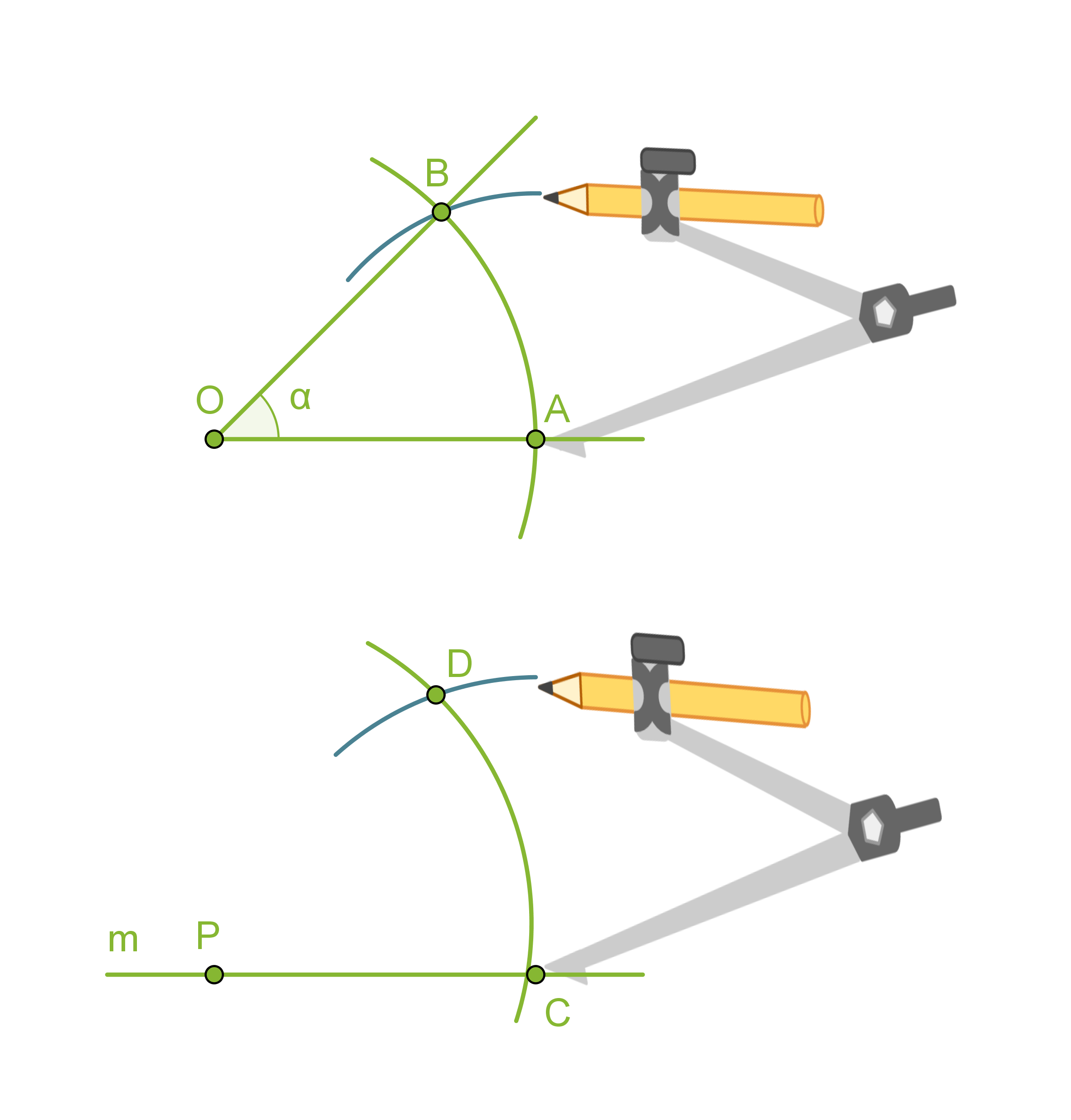
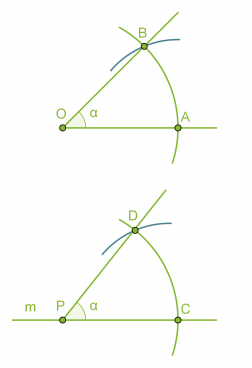
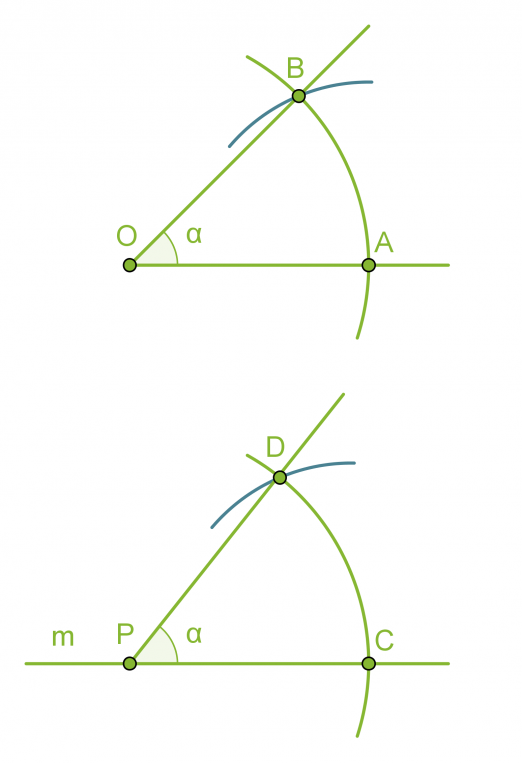
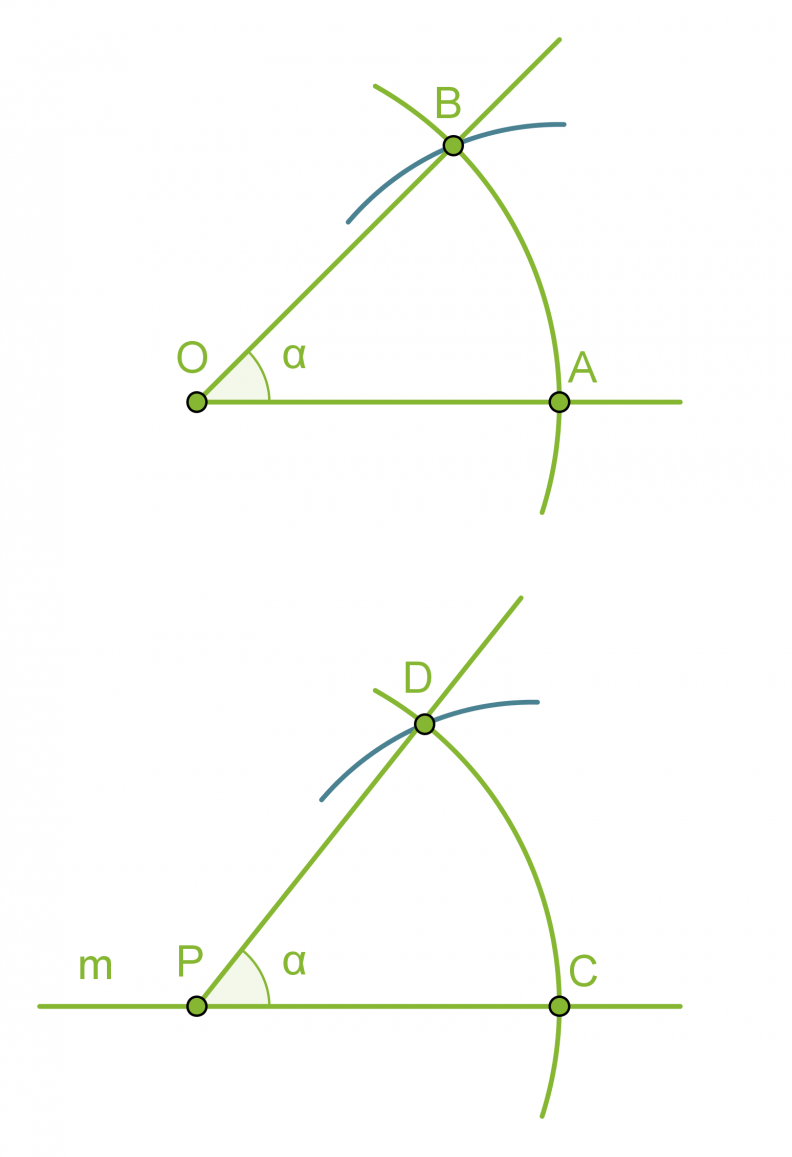
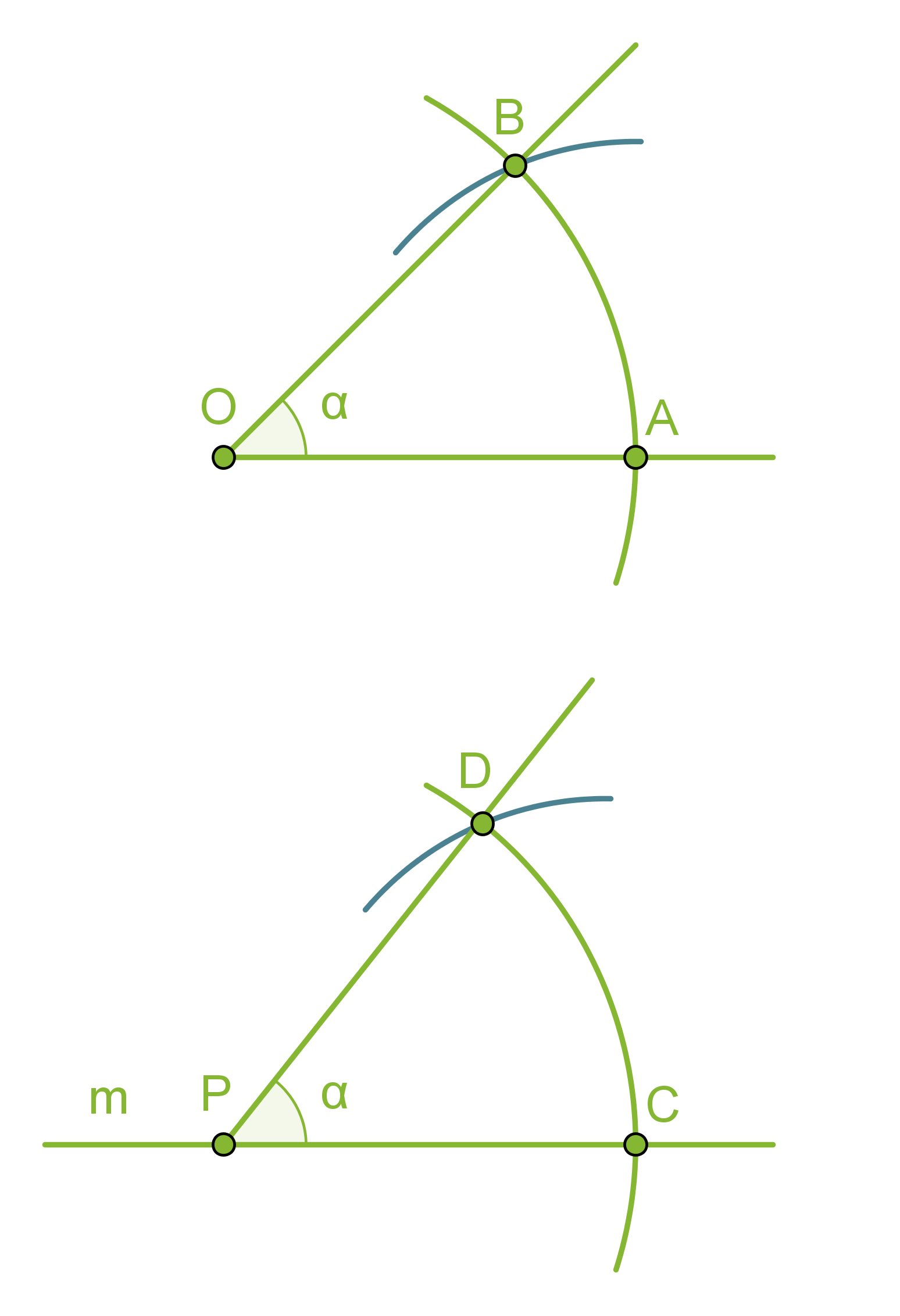
- Piirretään kaksi samansäteistä ympyräkaarta, joiden keskipisteinä ovat pisteet O ja P.
- Mitataan kaarta AB vastaava jänne harpilla ja erotetaan vastaavan mittainen jänne CD.
- Piirretään pisteestä P alkava puolisuora PD, jolloin muodostuu a:n suuruinen kulma CPD.