13. Kolmion, suunnikkaan ja puolisuunnikkaan pinta-ala
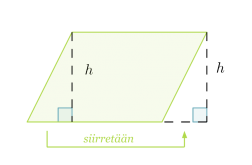
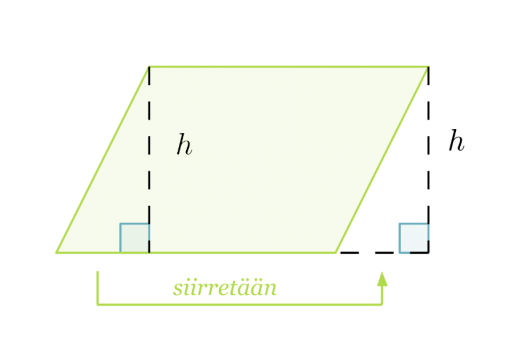
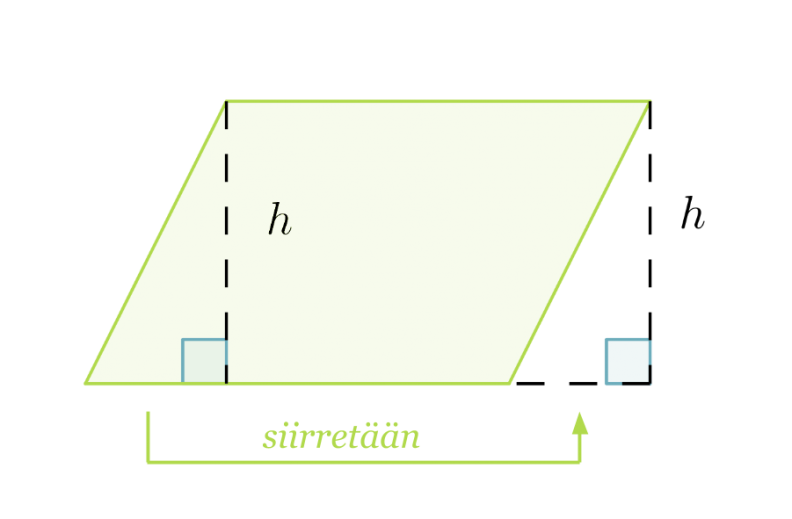
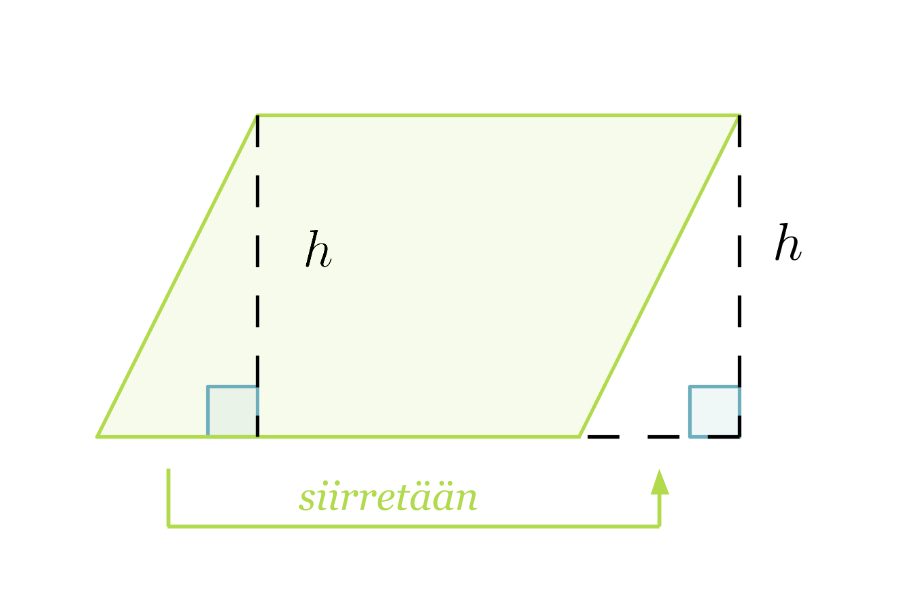
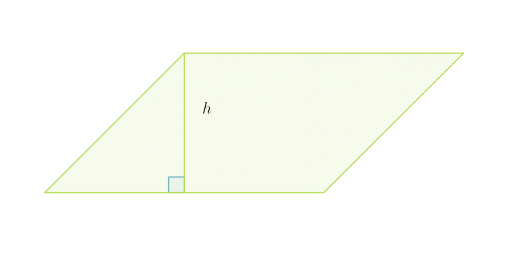
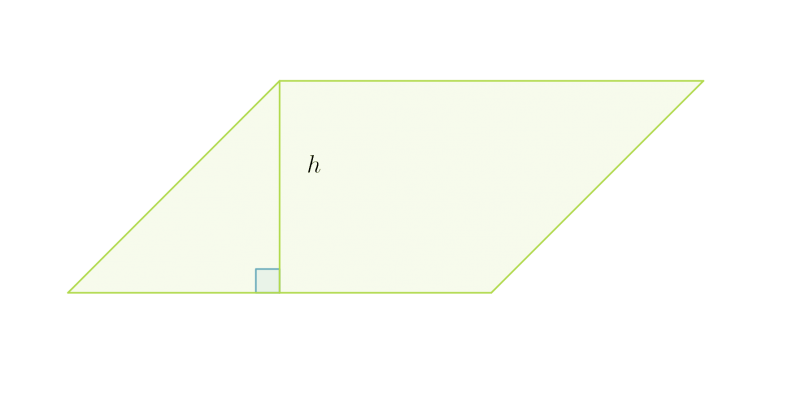
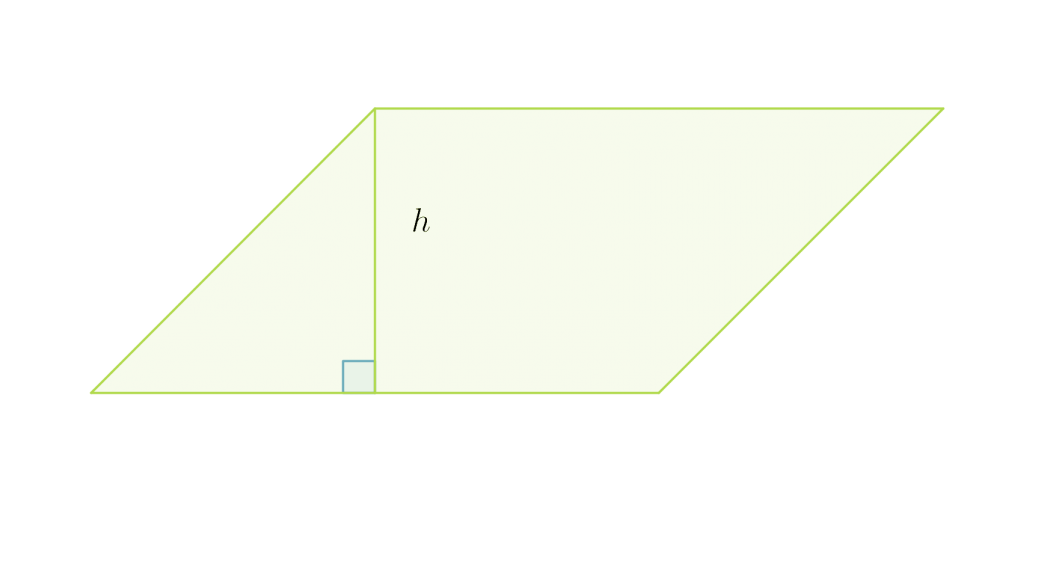
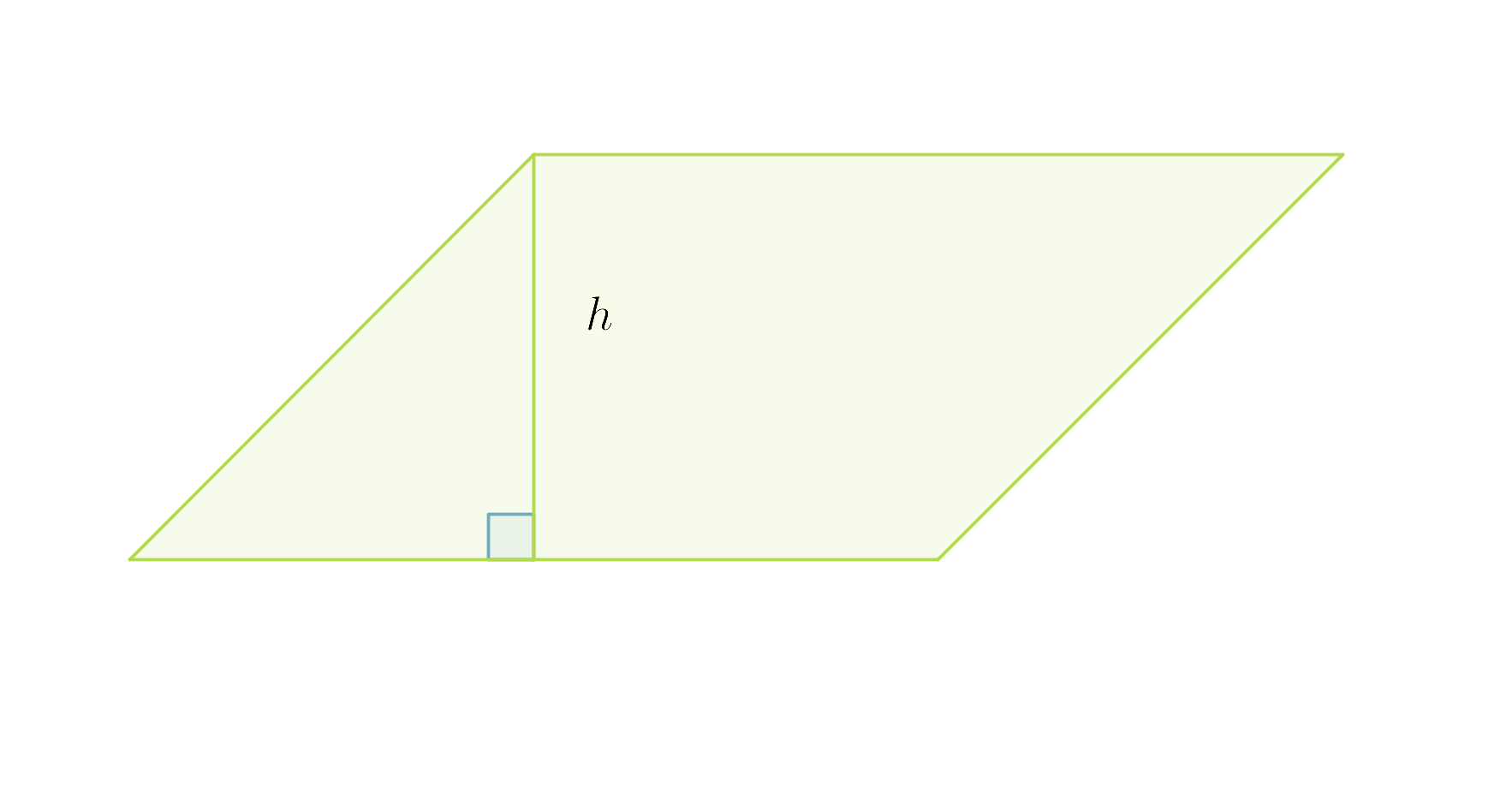
Suunnikas voidaan muodostaa suorakulmiosta leikkaamalla suorakulmion reunasta irti suorakulmainen kolmio ja siirtämällä irtileikattu kolmio suorakulmion vastakkaiseen reunaan. Suorakulmio ja suunnikas muodostuvat siis samoista osista, joten niillä on sama pinta-ala.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suunnikkaan pinta-ala on kannan ja vastaavan korkeuden tulo: A = a·h

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
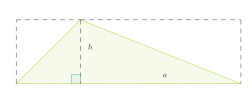
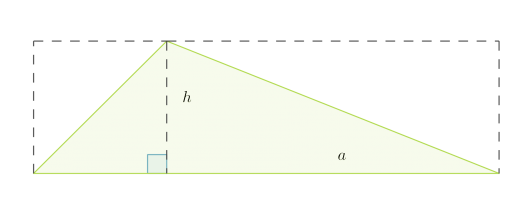
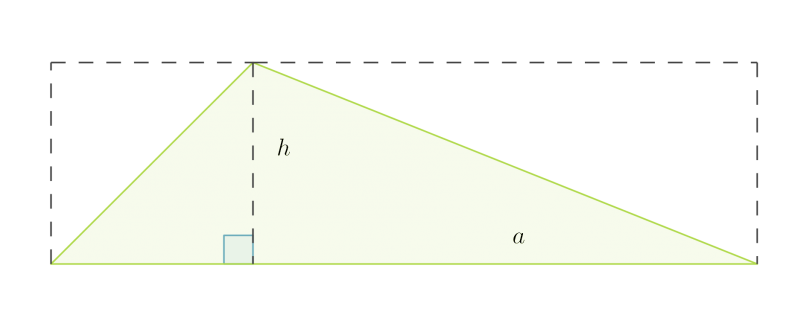
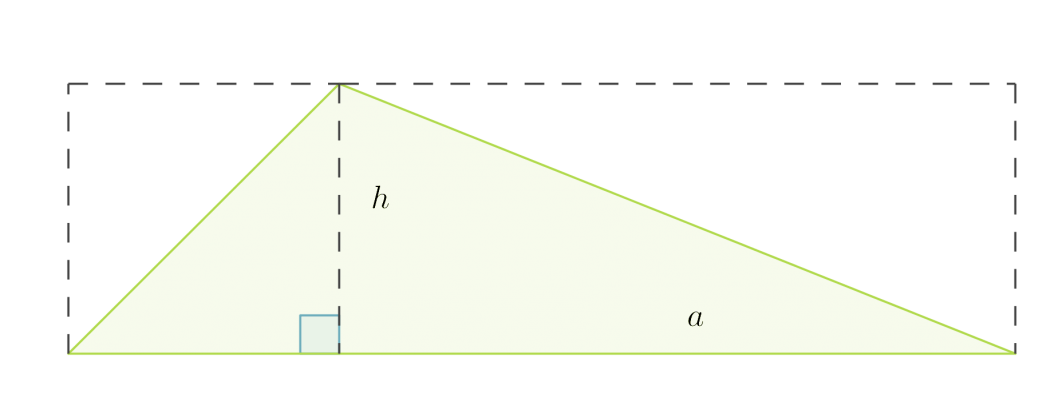
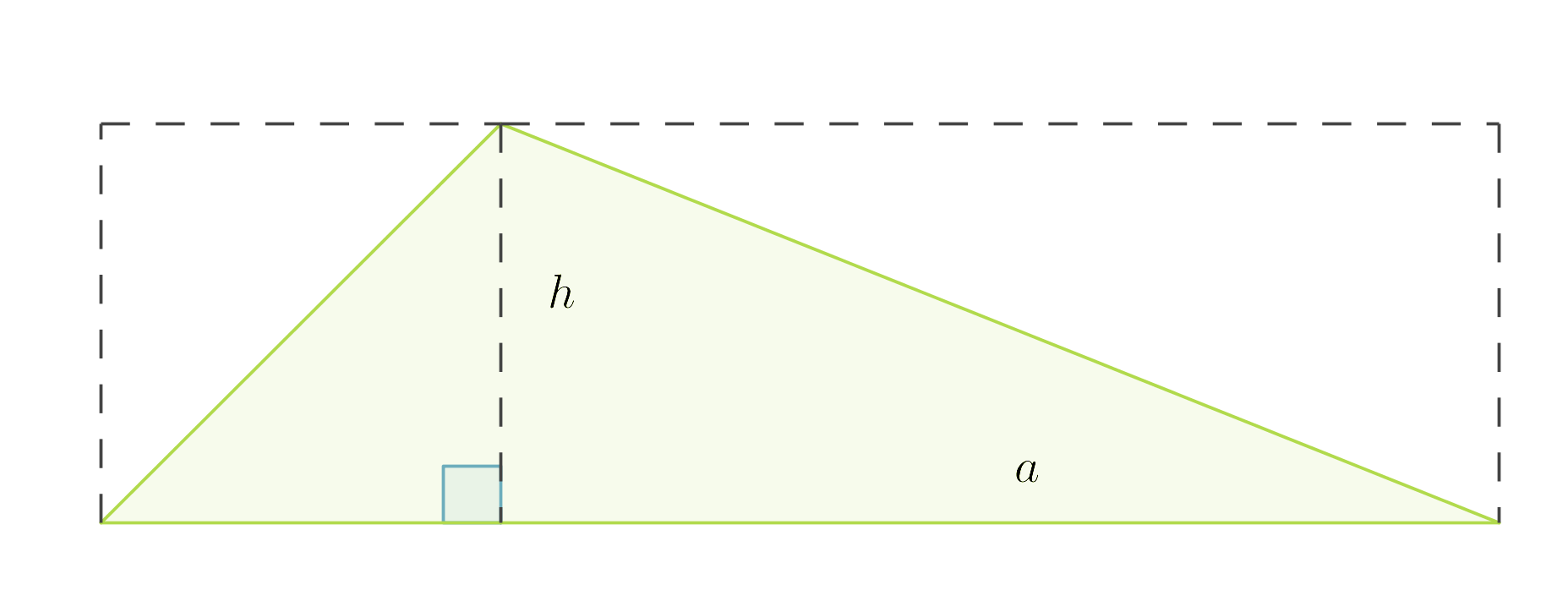
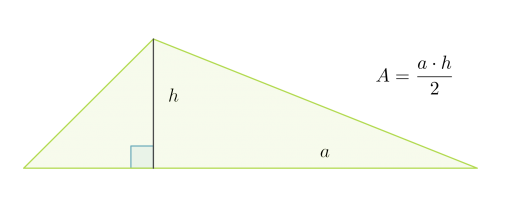
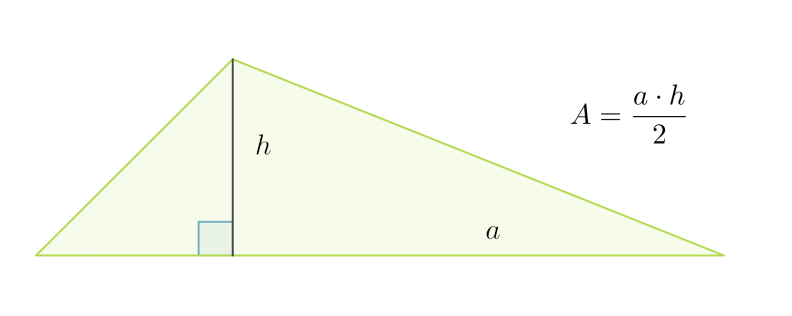
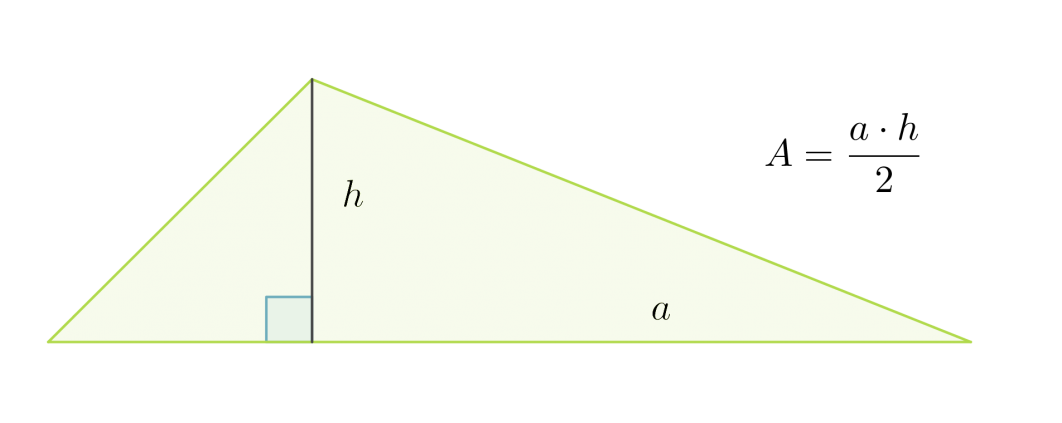
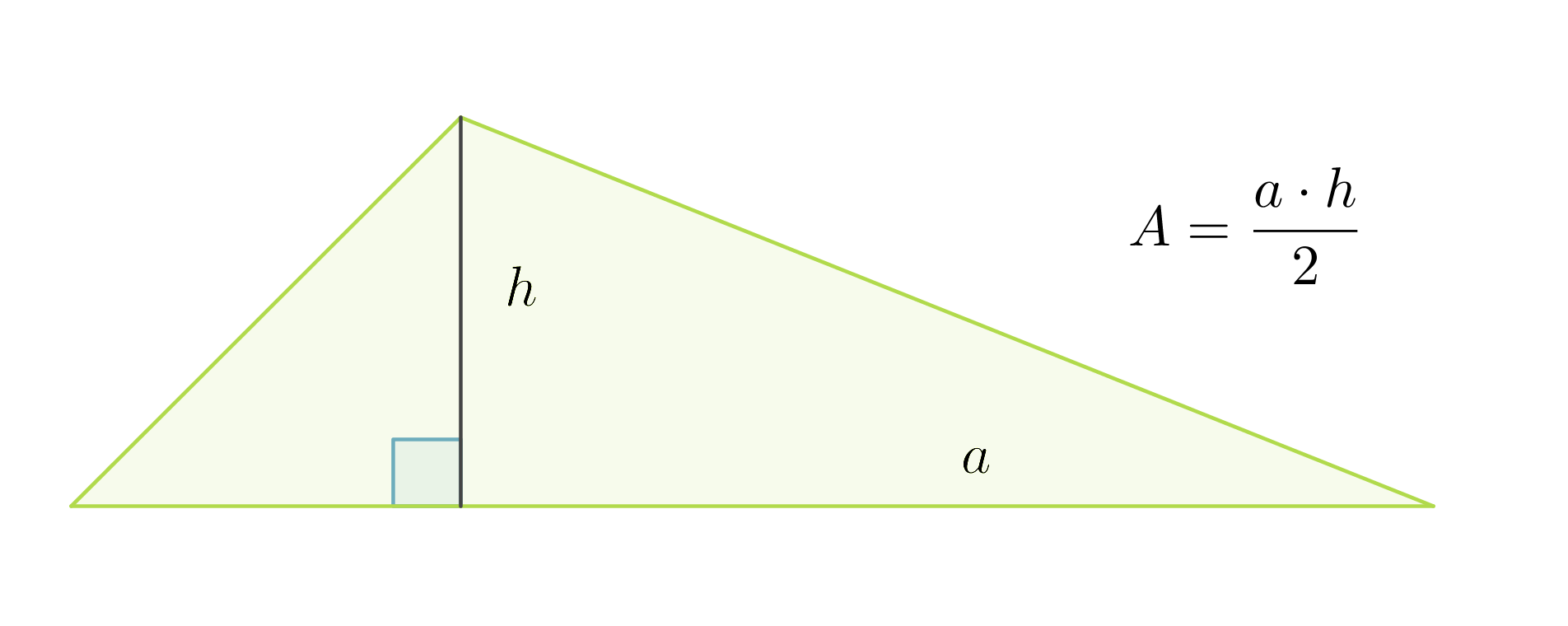
Kolmio voidaan täydentää suorakulmioksi kuvan katokoviiva-alueen mukaisesti. Lisätyt kolmiot muodostavat yhtä suuren alueen kuin alkuperäinen kolmio. Siksi kolmion pinta-ala saadaankin laskemalla suorakulmion pinta-ala ja jakamalla se kahdella.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kolmion pinta-ala on kannan ja vastaavan korkeuden tulo jaettuna kahdella:

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
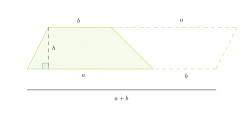
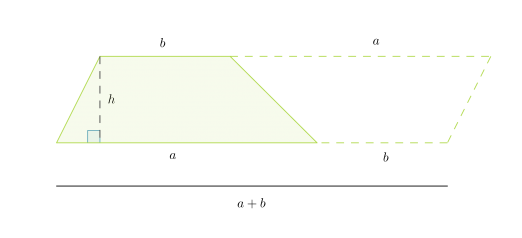
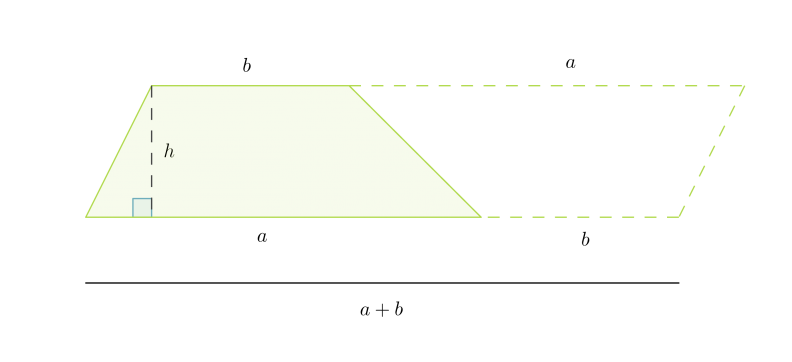
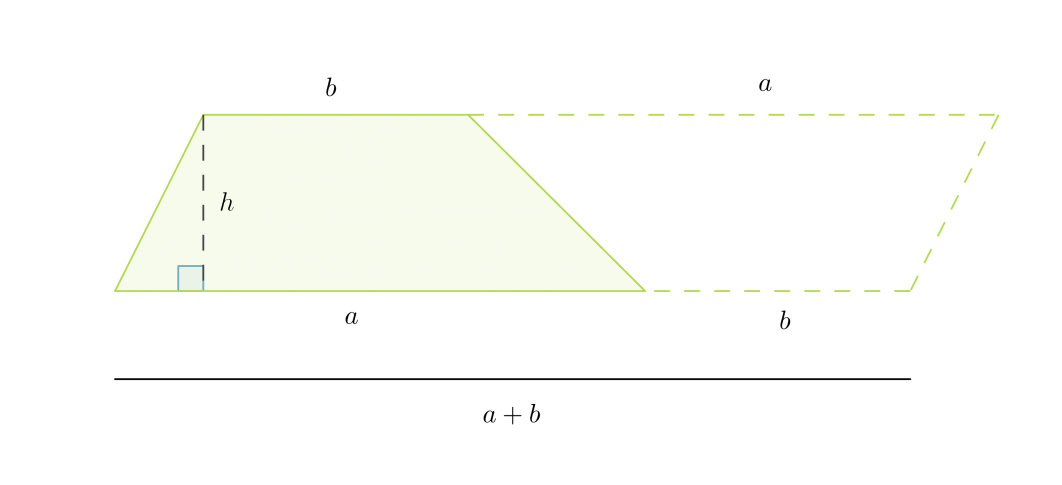
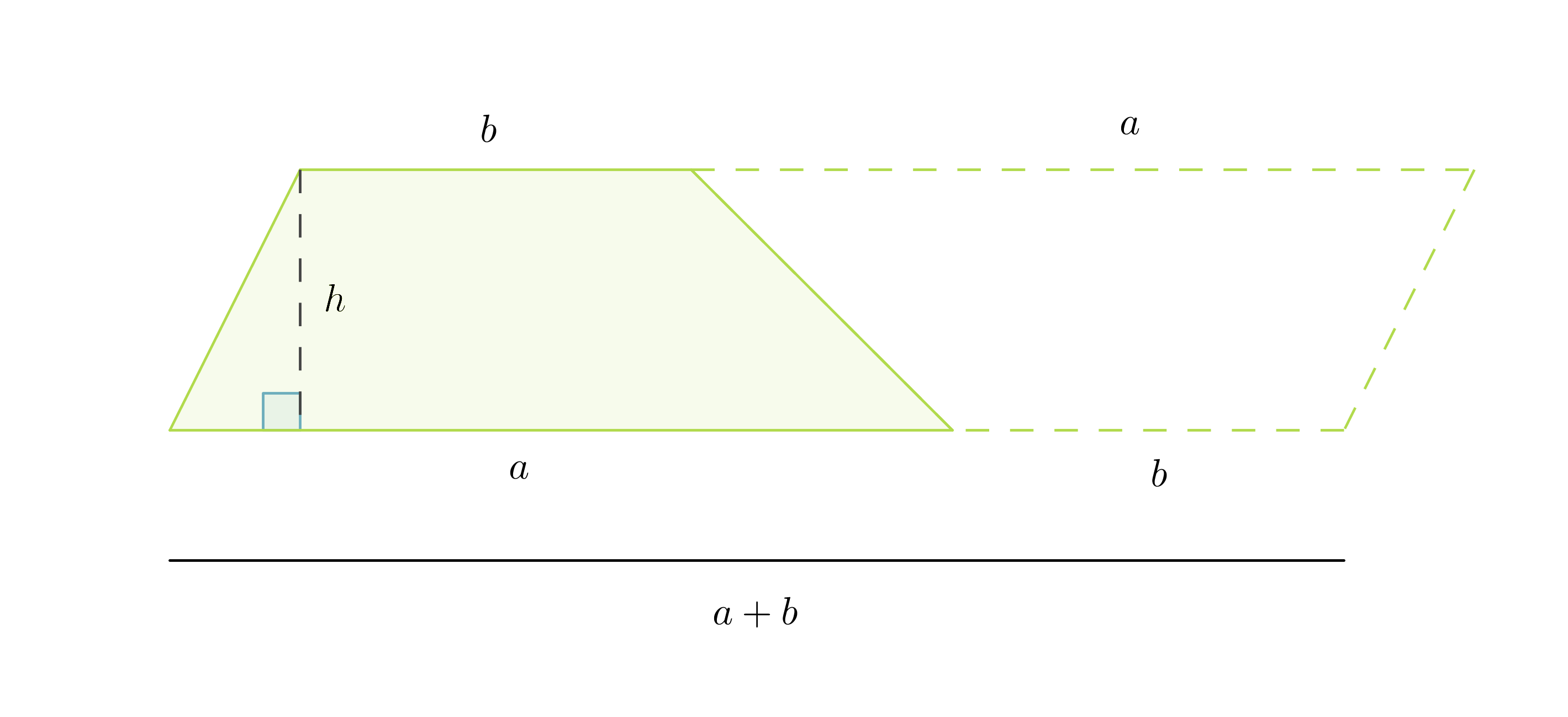
Kahdesta samankokoisesta puolisuunnikkaasta voidaan muodostaa kuvion mukainen suunnikas.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
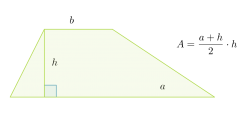
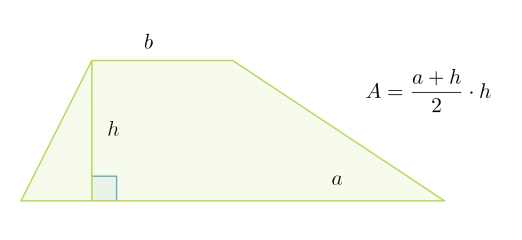
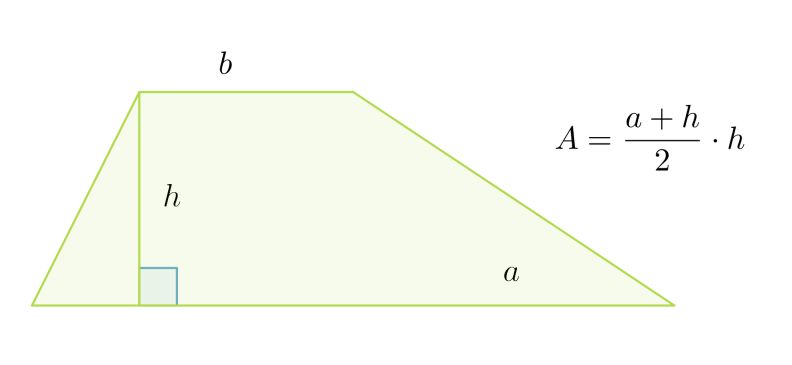
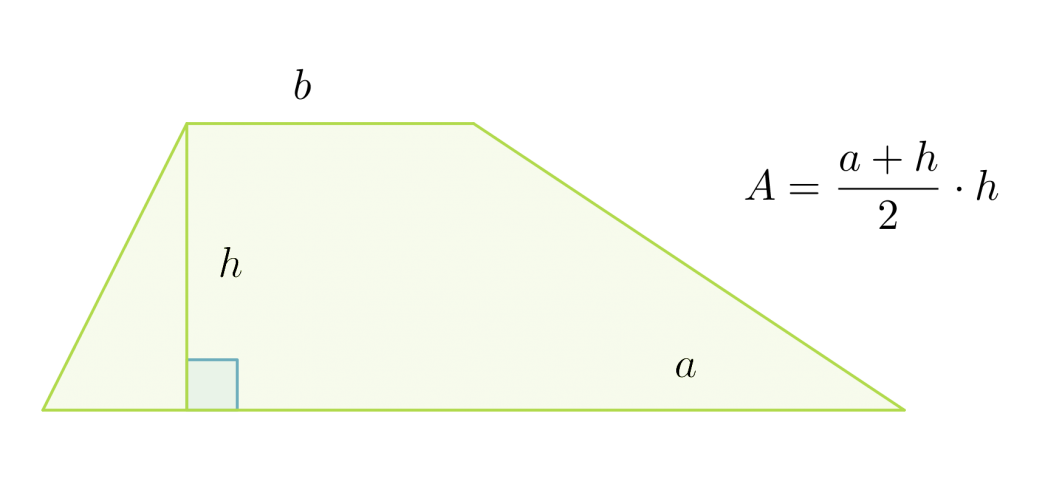
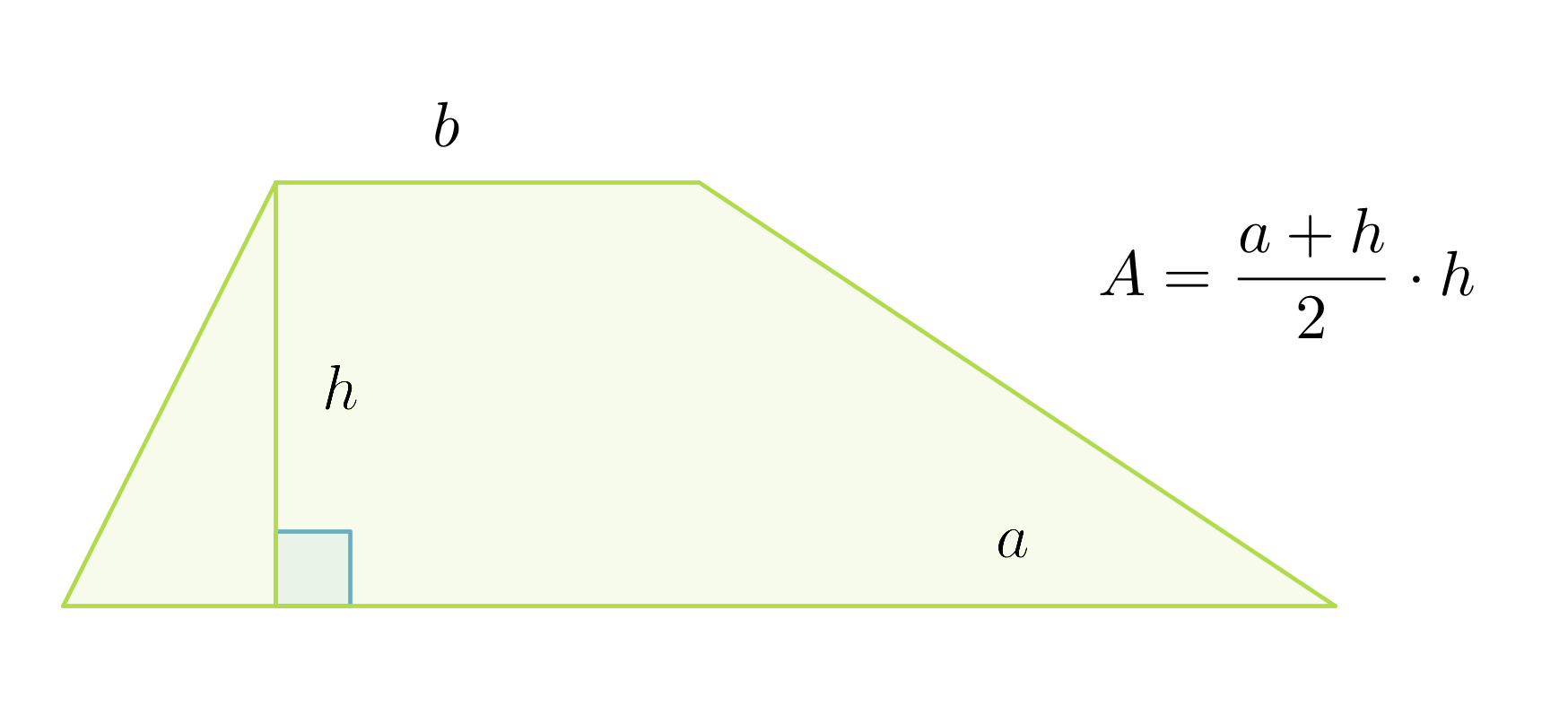
Suunnikkaan korkeus on puolisuunnikkaan korkeus h ja kanta puolisuunnikkaan kantojen summa a + b. Puolisuunnikkaan pinta-ala saadaan jakamalla muodostuneen suunnikkaan pinta-ala kahdella.
Puolisuunnikkaan pinta-ala on kantojen keskiarvon ja korkeuden tulo:
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Muiden monikulmioiden pinta-alat lasketaan siten, että monikulmio jaetaan kolmioihin tai nelikulmioihin ja niiden alat lasketaan yhteen. Kaikissa pinta-alalaskuissa on kiinnitettävä huomiota siihen, että jokainen mitta sijoitetaan laskukaavaan samoissa yksikössä.
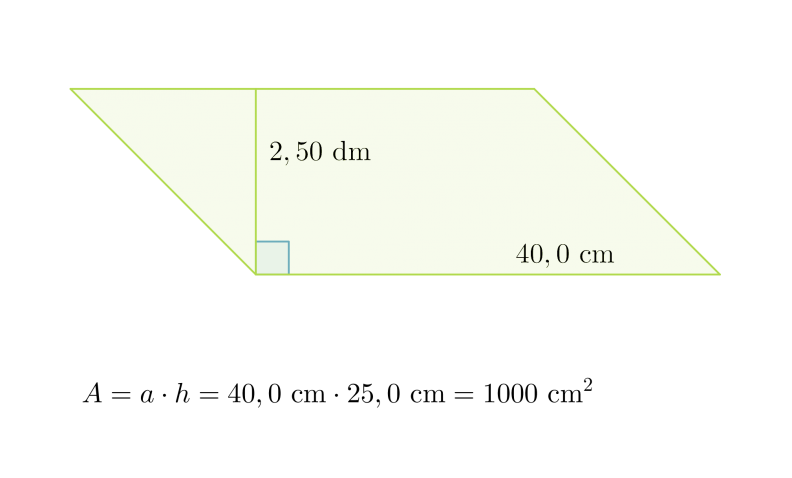
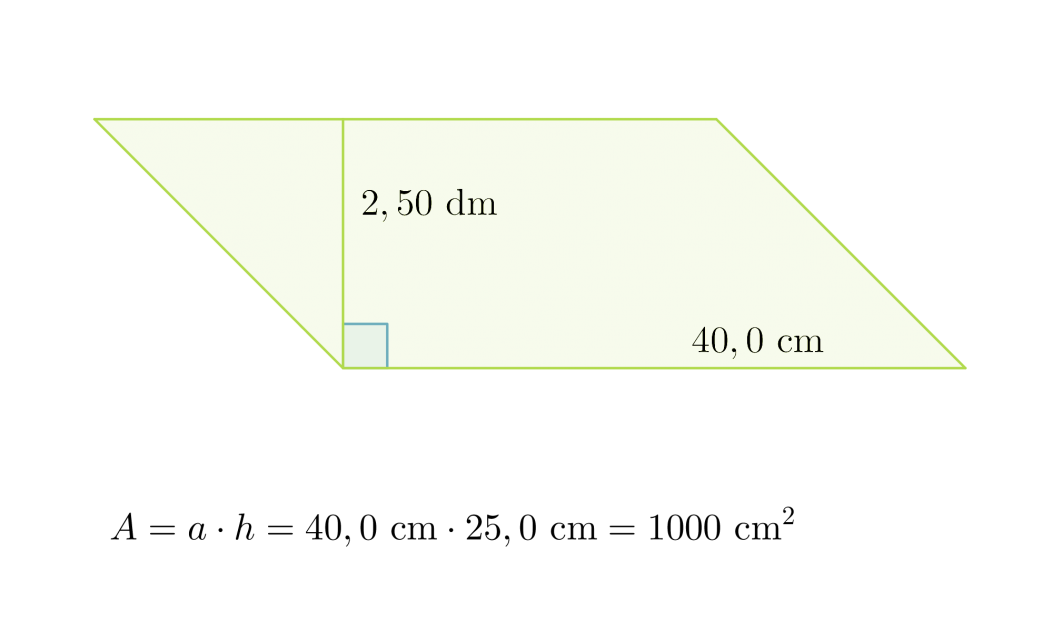
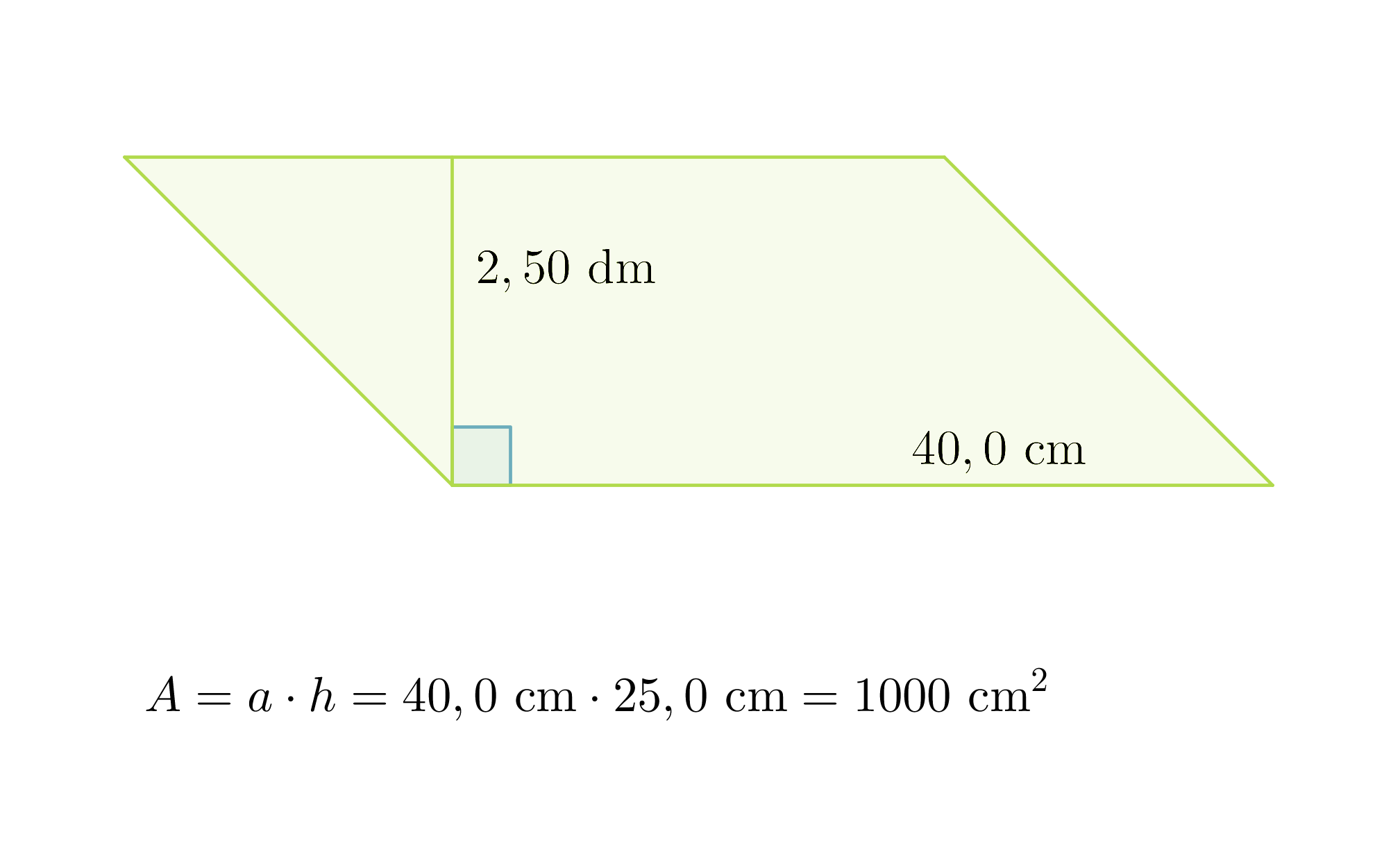
Esimerkki 1.
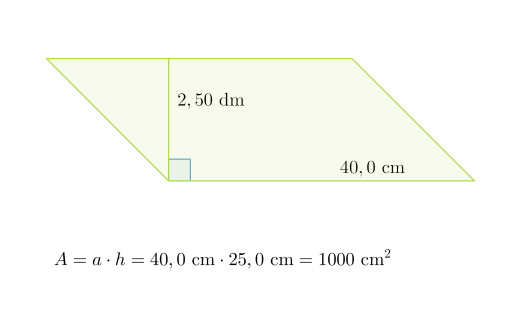
Lasketaan suunnikkaan pinta-ala.
Ennen mittojen kaavaan sijoittamista, ne on muutettava samaan yksikköön. Joten ilmoitetaan 2,50 desimetriä senttimetreinä: 2,50 dm = 25,0 cm.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
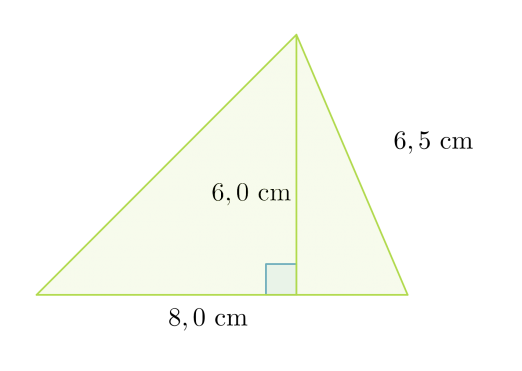
Esimerkki 2.
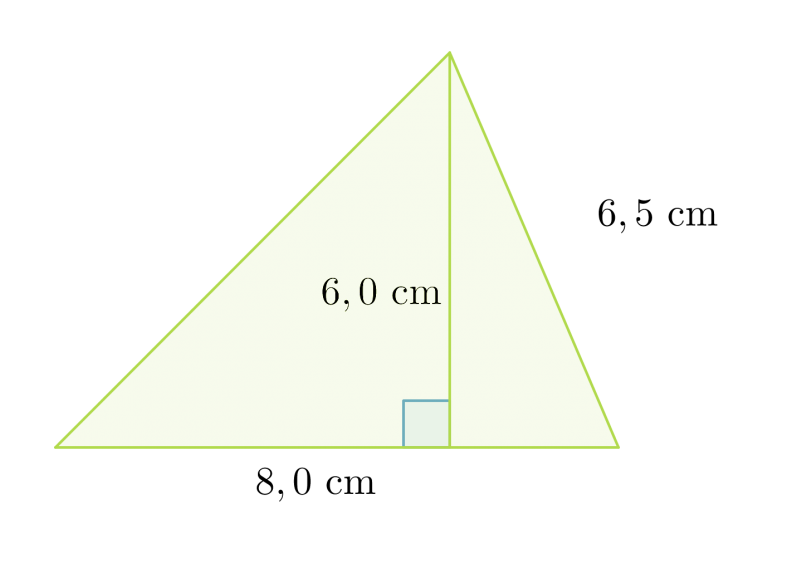
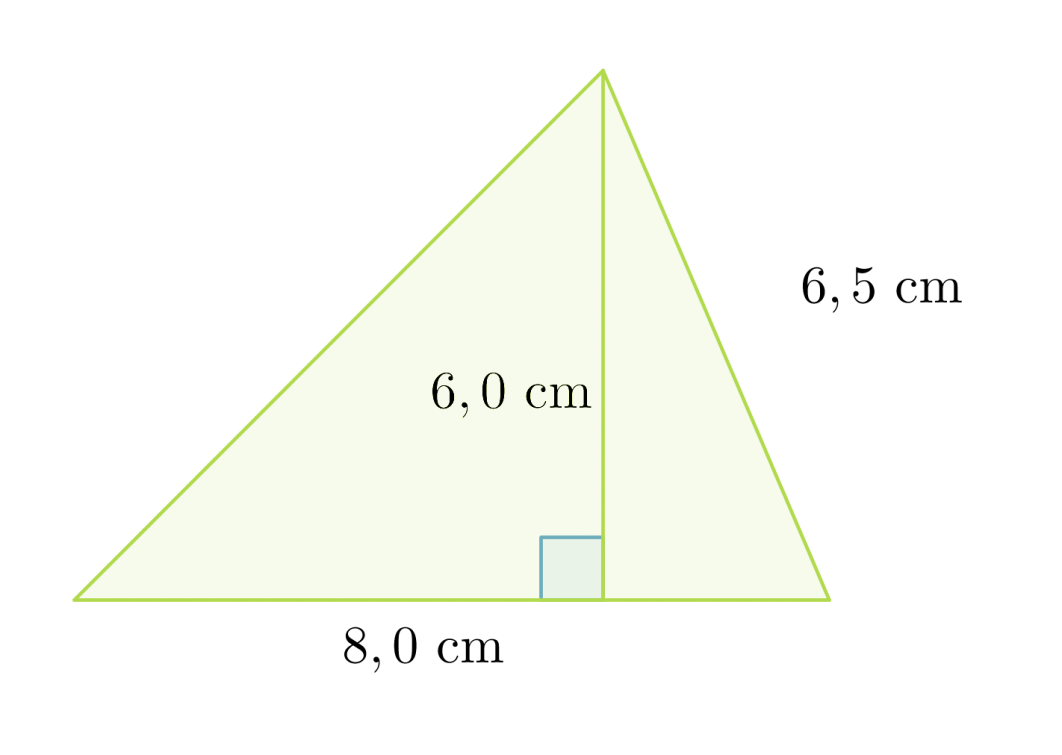
Lasketaan kolmion pinta-ala.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
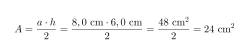
Klikkaa kuva suuremmaksi!
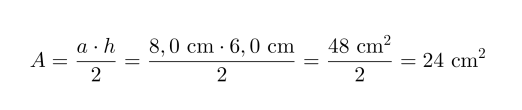
Klikkaa kuva suuremmaksi!
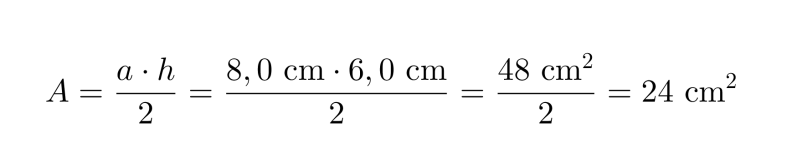
Klikkaa kuva suuremmaksi!
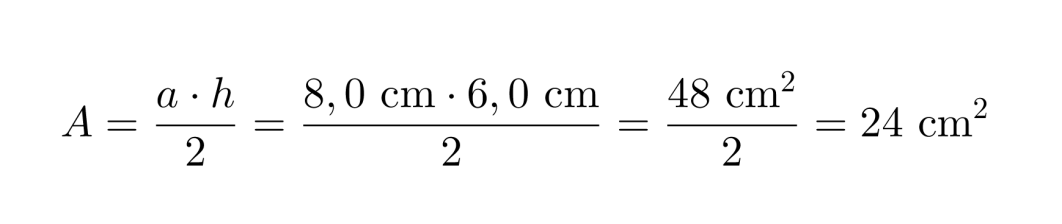
Klikkaa kuva suuremmaksi!
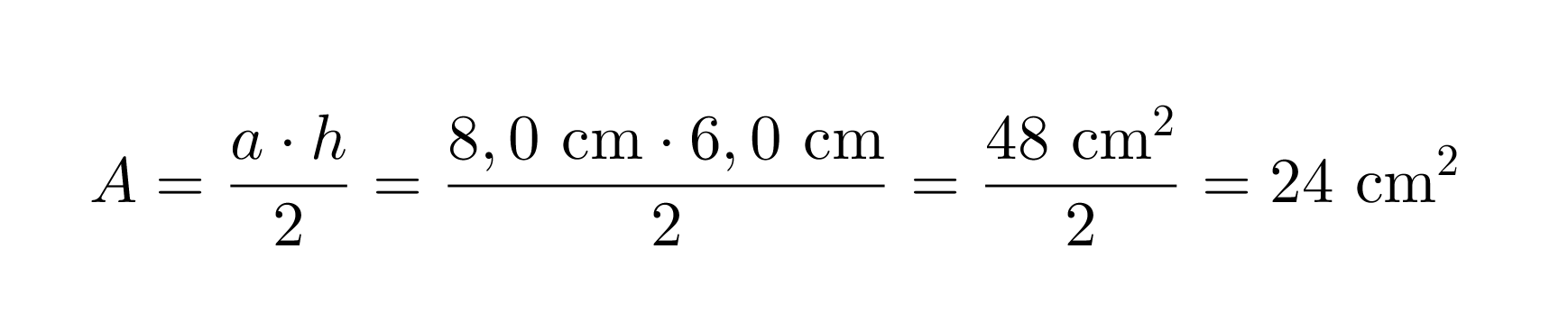
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus
Kolmion pinta-ala on 24 cm2.
Huom! Suunnikkaassa, kolmiossa ja puolisuunnikkaassa korkeusjanat ja sivujanat ovat erimittaisia, eikä niiden pinta-alojen laskemisessa voida käyttää sivujanojen pituuksia.
Esimerkki 3.
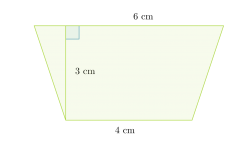
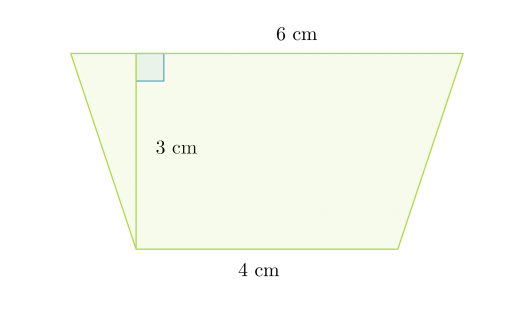
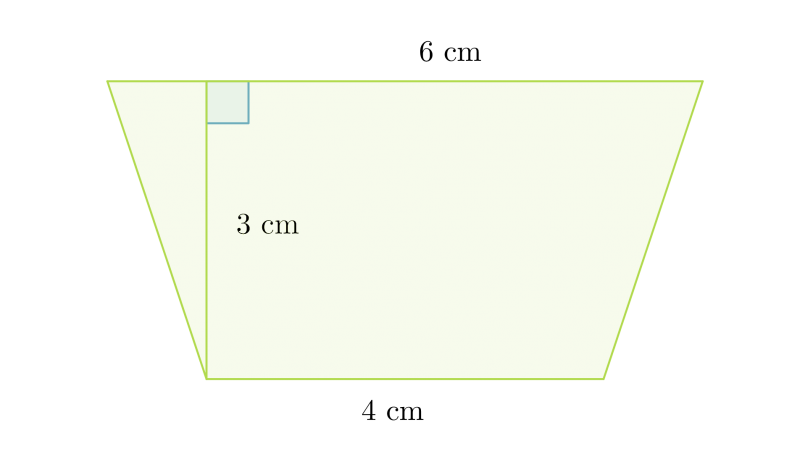
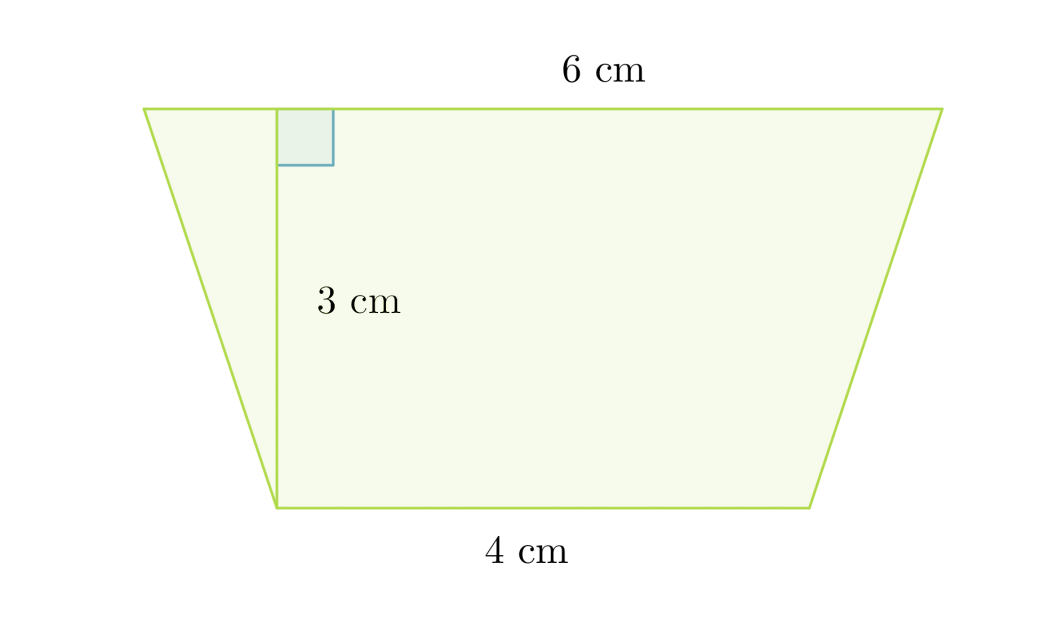
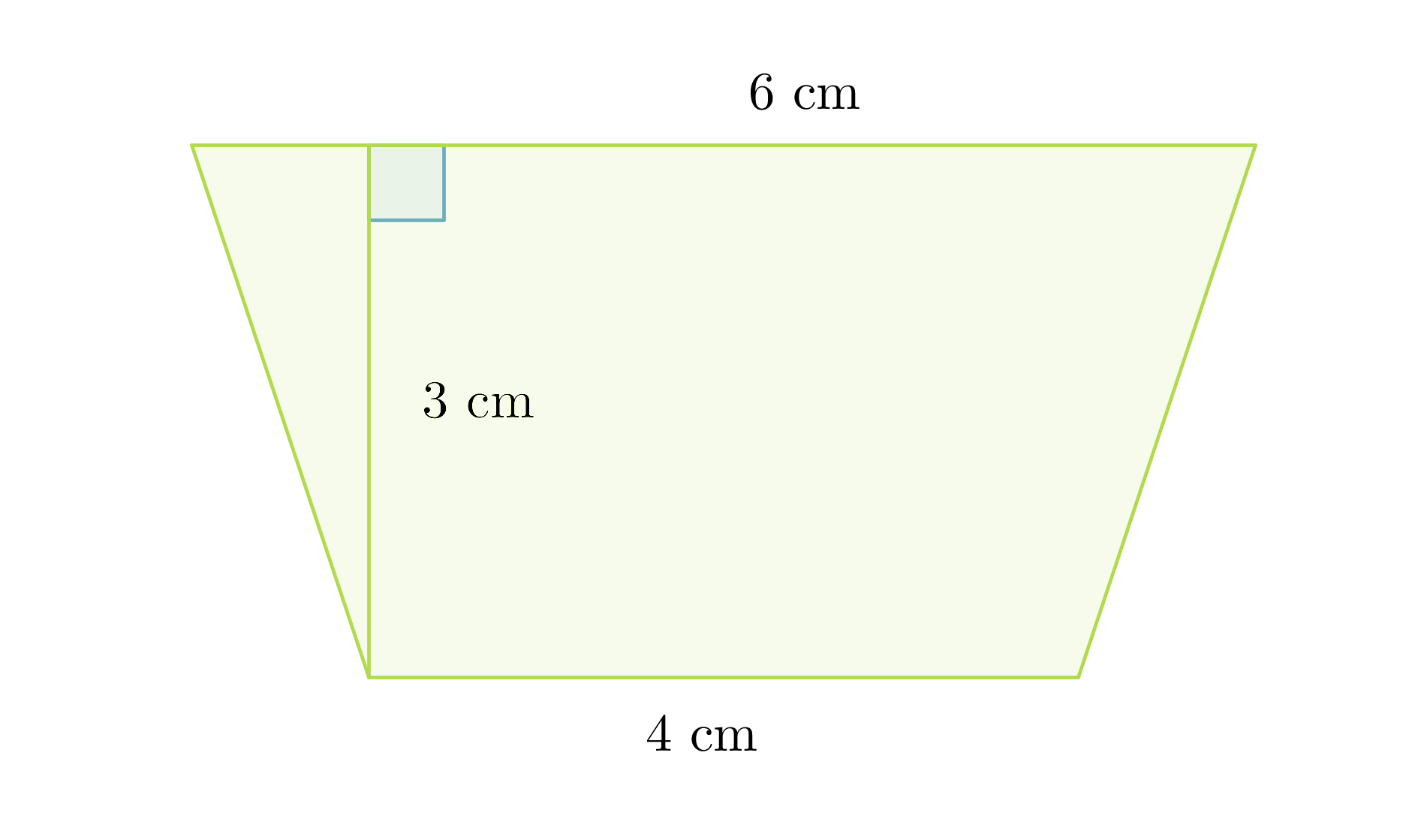
Lasketaan puolisuunnikkaan pinta-ala, kun sen kannat ovat 4,0 cm ja 6,0 cm sekä näiden välinen etäisyys on 3,0 cm.
Geometrian sanallisten tehtävien ratkaiseminen kannattaa aloittaa piirtämällä tilanteesta kuva, johon merkitään kaikki annetut mitat:
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Sijoitetaan arvot puolisuunnikkaan pinta-alakaavaan:

Klikkaa kuva suuremmaksi!
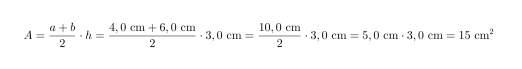
Klikkaa kuva suuremmaksi!
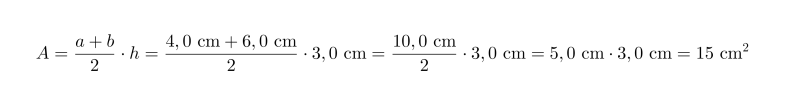
Klikkaa kuva suuremmaksi!
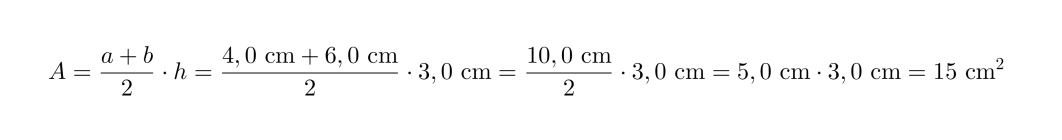
Klikkaa kuva suuremmaksi!
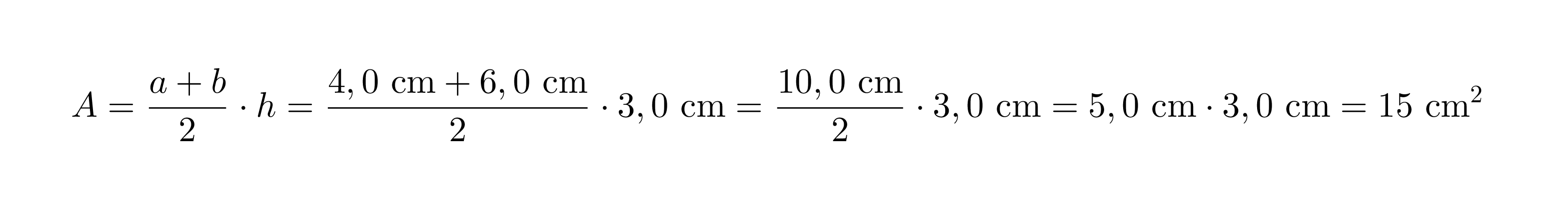
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus:
Puolisuunnikkaan pinta-ala on 15 cm2
Avoin matematiikka 7Osio 2: Kuvioiden luokittelua ja pinta-aloja23.5.2014