1. Samankantaisten potenssien tulo
Merkinnässä 24 =2·2·2·2 = 16 lukua 2 sanotaan kantaluvuksi, lukua 4 eksponentiksi ja lukua 16 potenssin arvoksi. Potenssin kantaluvun kanssa on oltava tarkkana. Jos sulkeita ei käytetä, eksponentti vaikuttaa vain siihen lukuun, joka on suoraan eksponentin alla.
Esimerkki 1.
Sievennetään potenssit.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tulossa 42 · 43 on molempien potenssien kantaluku sama. Merkintää kutsutaankin samankantaisten potenssien tuloksi.
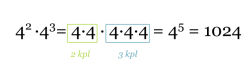
Klikkaa kuva suuremmaksi!
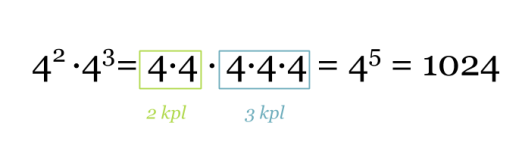
Klikkaa kuva suuremmaksi!
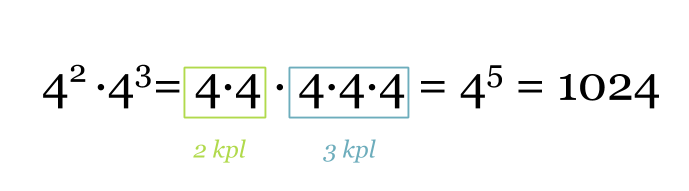
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Sievennetään potenssit.

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Samankantaisien potenssien kertolaskuissa on usein mukana muitakin tekijöitä, joita voidaan yhdistellä erikseen keskenään. Jos tulossa on muuttujia eli kirjaimia, kertomerkit jätetään merkitsemättä lukuarvon ja muuttujan väliin tai useamman muuttujan väliin.
Esimerkki 3.
Sievennetään potenssit.

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Samankantaisten potenssien tulo
Samankantaiset potenssit kerrotaan keskenään siten, että eksponentit lasketaan yhteen. Kantaluku pysyy samana.
am · an = am+n