2. Samankantaisten potenssien osamäärä ja nollaeksponentti
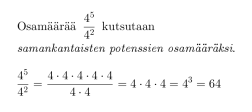
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
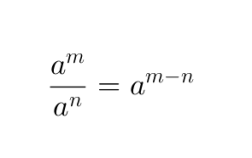
Klikkaa kuvaa suurentaaksesi!
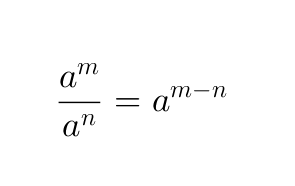
Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Esimerkki 1.
Sievennetään potenssit.
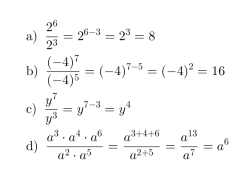
Klikkaa kuvaa suurentaaksesi!
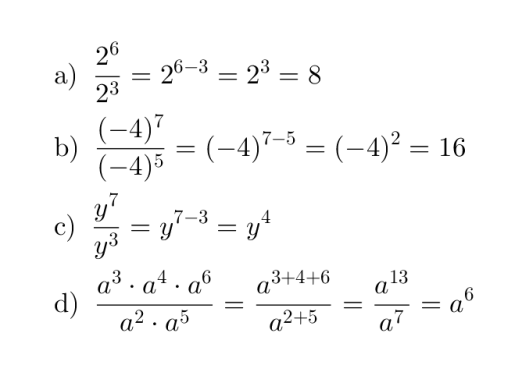
Klikkaa kuvaa suurentaaksesi!
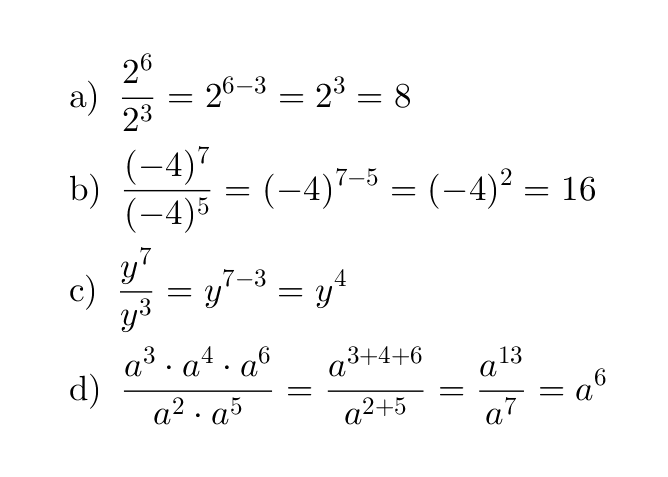
Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Myös samankantaisien potenssien osamäärässä on usein mukana muitakin tekijöitä, joten on syytä olla tarkkana kantaluvun kanssa.
Esimerkki 2.
Sievennetään potenssit.

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Tarkastellaan seuraavaksi jakolaskua 43/43 kahdella eri tavalla. Sievennetään lauseke samankantaisten potenssien osamäärän avulla sekä supistamalla.

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Nollaeksponentti
Jos eksponenttina on nolla, on potenssin arvo aina 1. Kantalukuna ei kuitenkaan saa olla nolla.
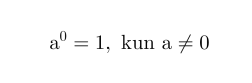
Klikkaa kuvaa suurentaaksesi!
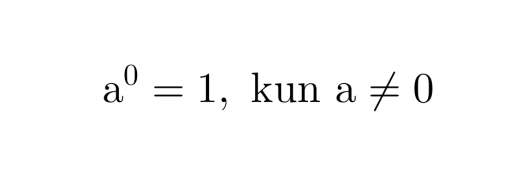
Klikkaa kuvaa suurentaaksesi!
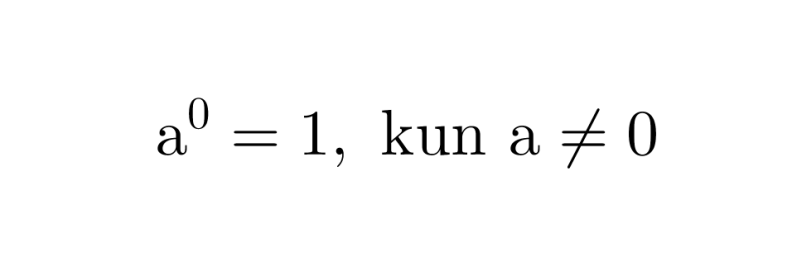
Klikkaa kuvaa suurentaaksesi!
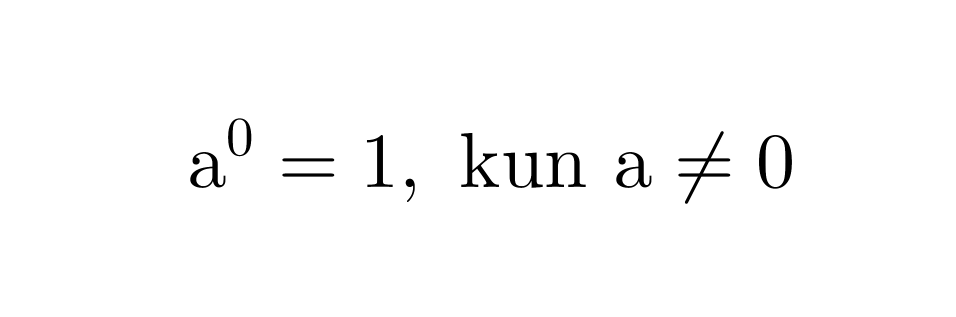
Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Esimerkki 3.
Sievennetään potenssit.
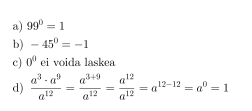
Klikkaa kuvaa suurentaaksesi!
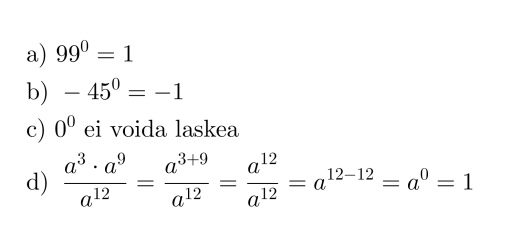
Klikkaa kuvaa suurentaaksesi!
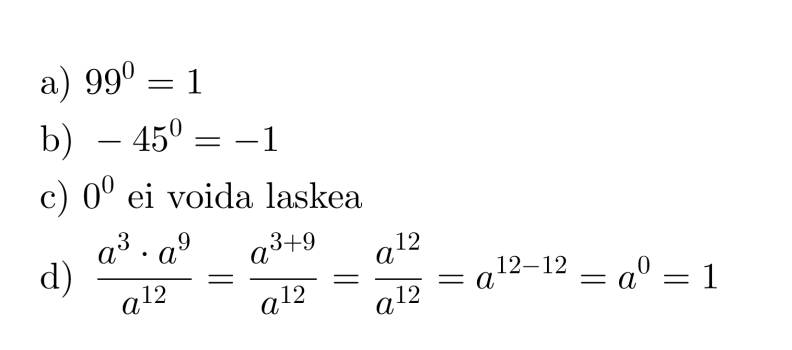
Klikkaa kuvaa suurentaaksesi!
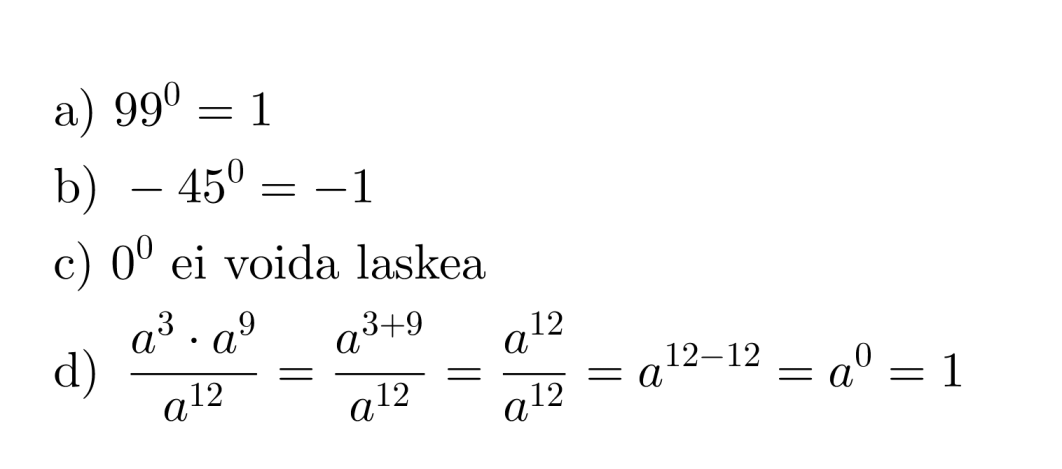
Klikkaa kuvaa suurentaaksesi!
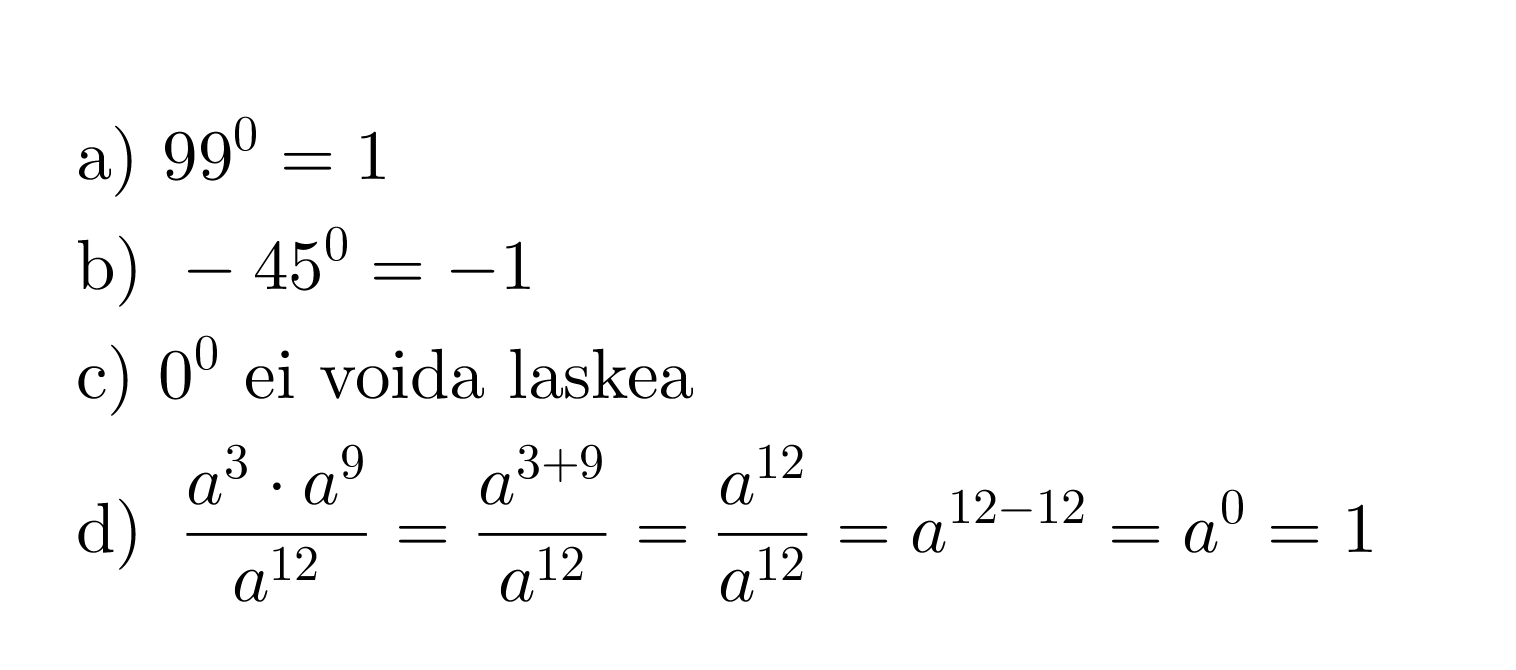
Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
Samankantaisten potenssien osamäärä
Samankantaiset osamäärät jaetaan keskenään siten, että osoittajan eksponentista vähennetään nimittäjän eksponentti. Kantaluku pysyy samana.