4. Negatiivinen eksponentti
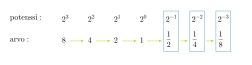
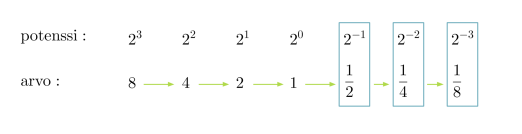
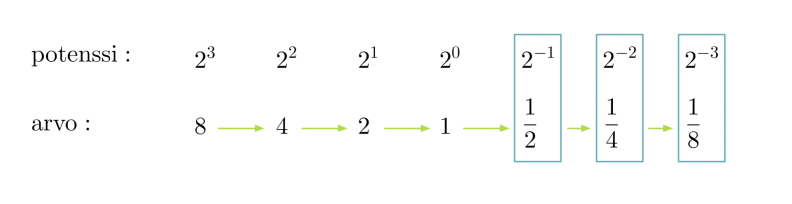
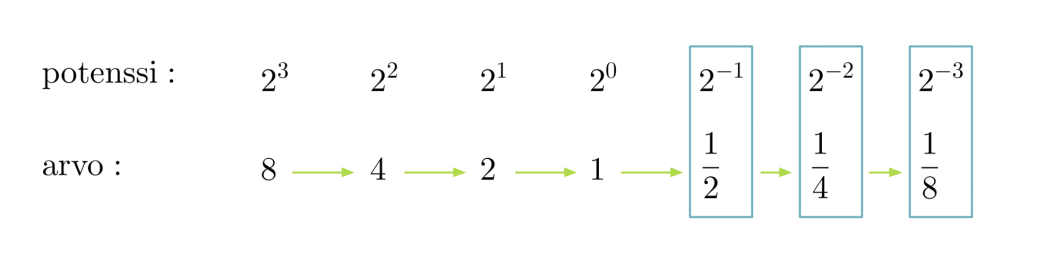
Tarkastellaan luvun kaksi potensseja sekä potenssien arvoja.
Klikkaa kuvaa suurentaaksesi!
Klikkaa kuvaa suurentaaksesi!
Klikkaa kuvaa suurentaaksesi!
Klikkaa kuvaa suurentaaksesi!
Klikkaa kuvaa suurentaaksesi!

Klikkaa kuvaa suurentaaksesi!
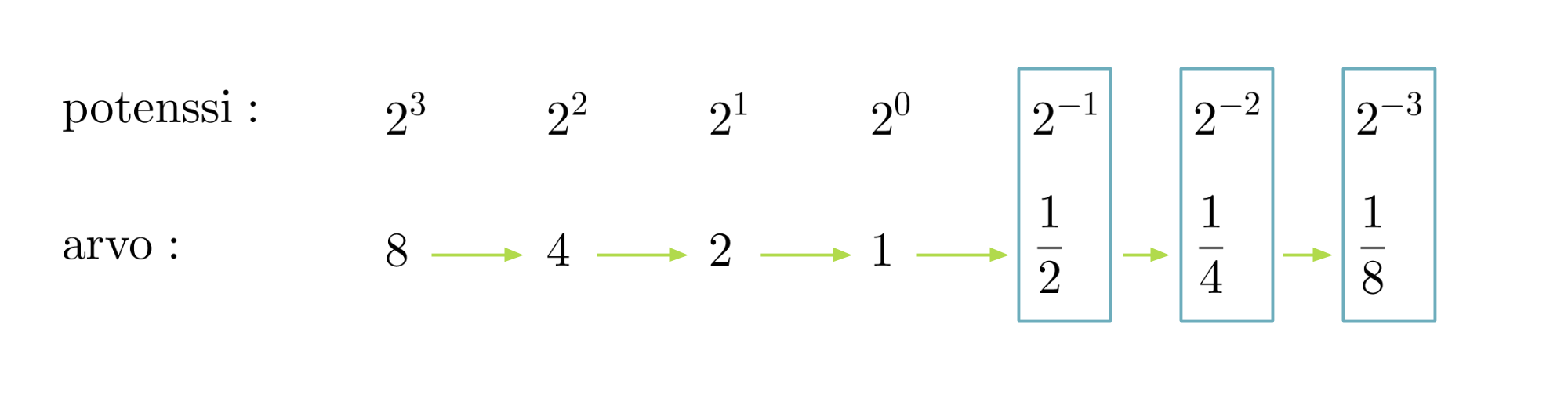
Oikealta vasemmalle mentäessä luvun kaksi eksponentti pienenee yhdellä. Potenssin arvo saadaan jakamalla edellisen potenssin arvo kahdella. Samaa menettelyä voidaan jatkaa myös negatiivisten eksponenttien puolelle.
Verrataan keskenään potenssien 23 ja 2-3 arvoja ja havaitaan, että molemmissa esiintyy luku kahdeksan. Vastaavasti, jos eksponenttina on 2 tai –2, esiintyy arvossa luku 4.

Klikkaa kuva suuremmaksi!
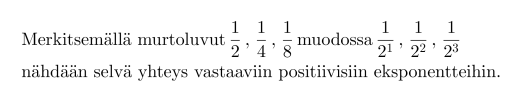
Klikkaa kuva suuremmaksi!
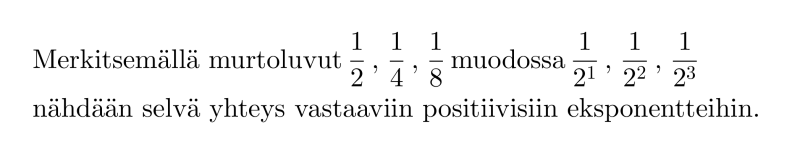
Klikkaa kuva suuremmaksi!
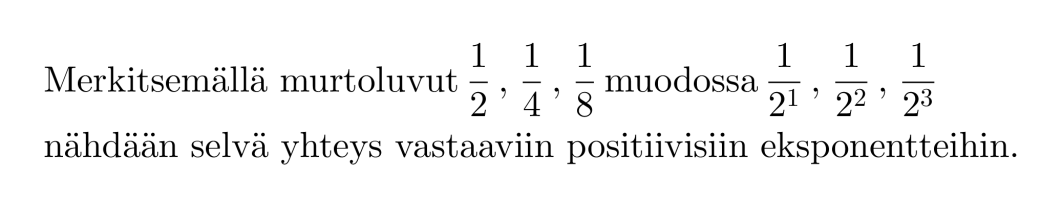
Klikkaa kuva suuremmaksi!
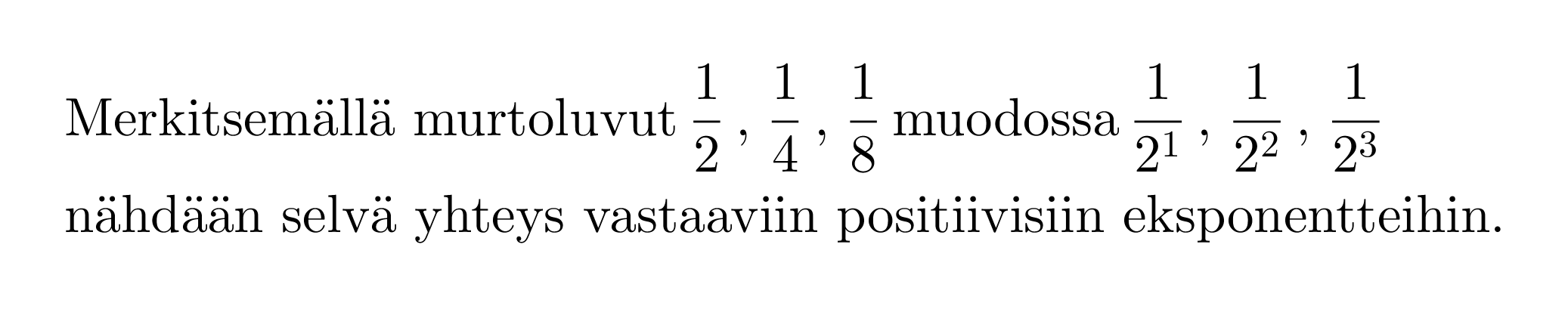
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
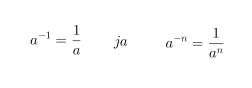
Klikkaa kuva suuremmaksi!
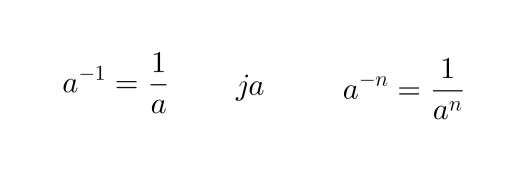
Klikkaa kuva suuremmaksi!
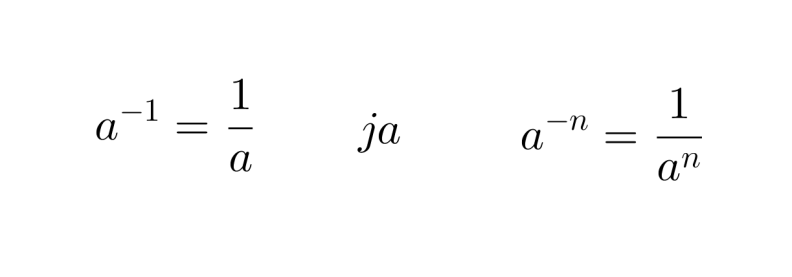
Klikkaa kuva suuremmaksi!
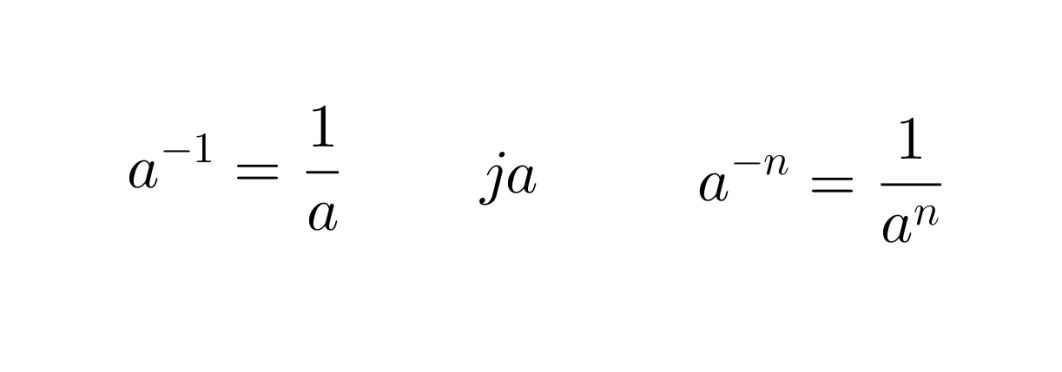
Klikkaa kuva suuremmaksi!
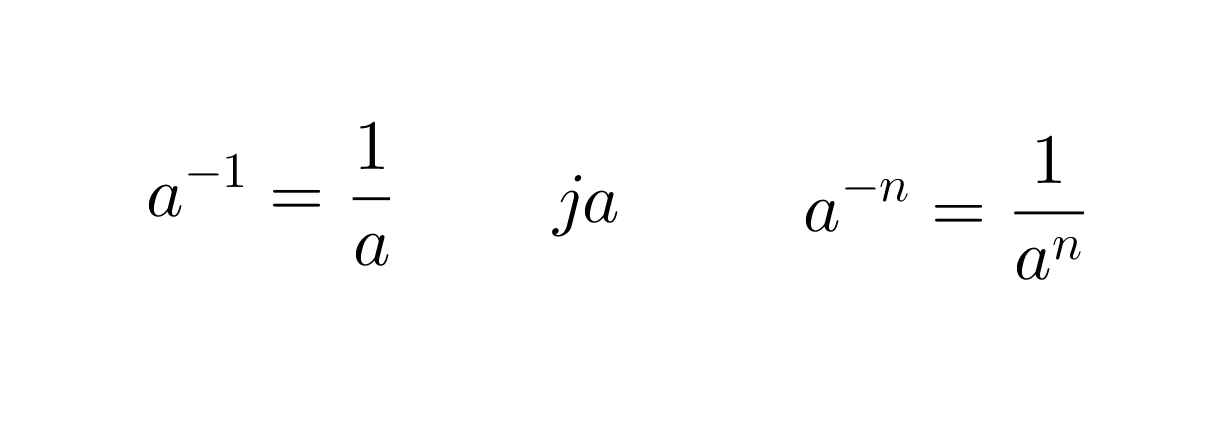
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Potenssin laskusäännöt ovat voimassa myös negatiivisille eksponenteille.
Esimerkki 1.
Kirjoitetaan murtolukuna.
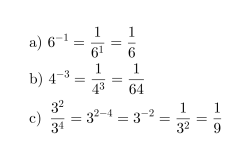
Klikkaa kuva suuremmaksi!
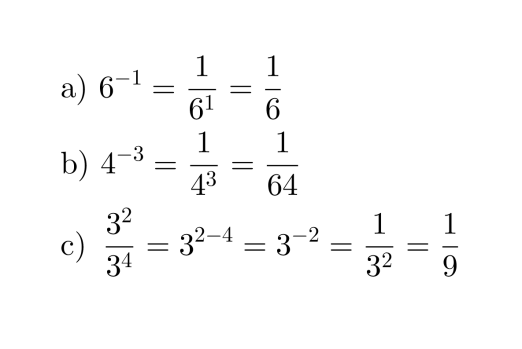
Klikkaa kuva suuremmaksi!
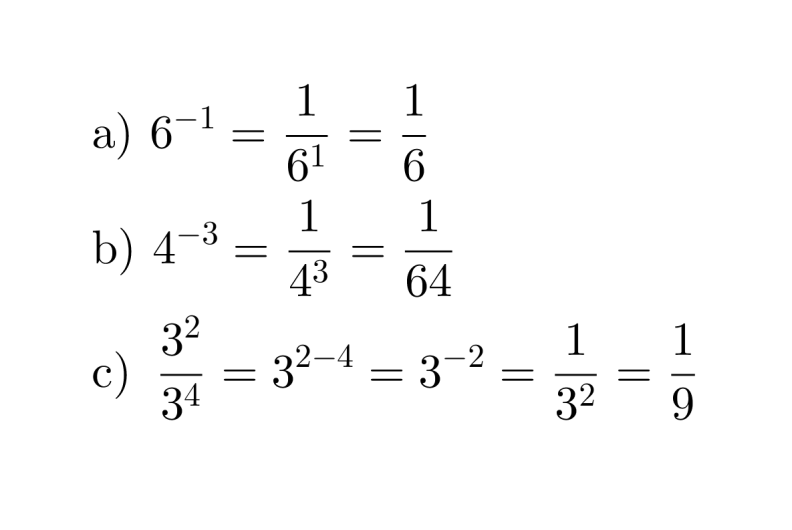
Klikkaa kuva suuremmaksi!
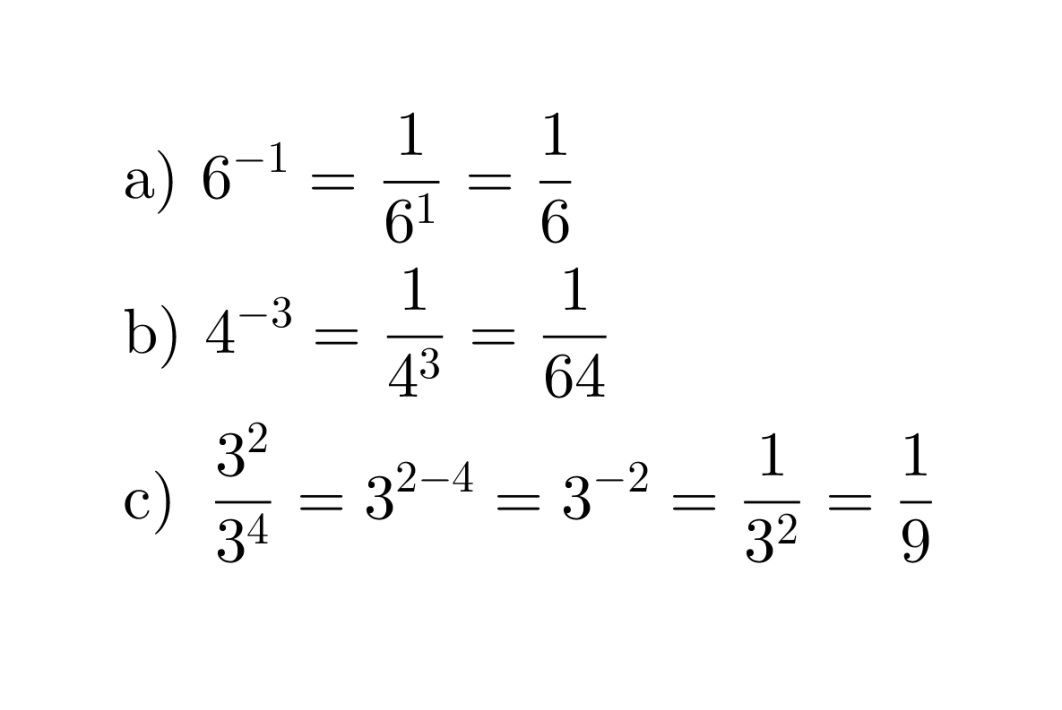
Klikkaa kuva suuremmaksi!
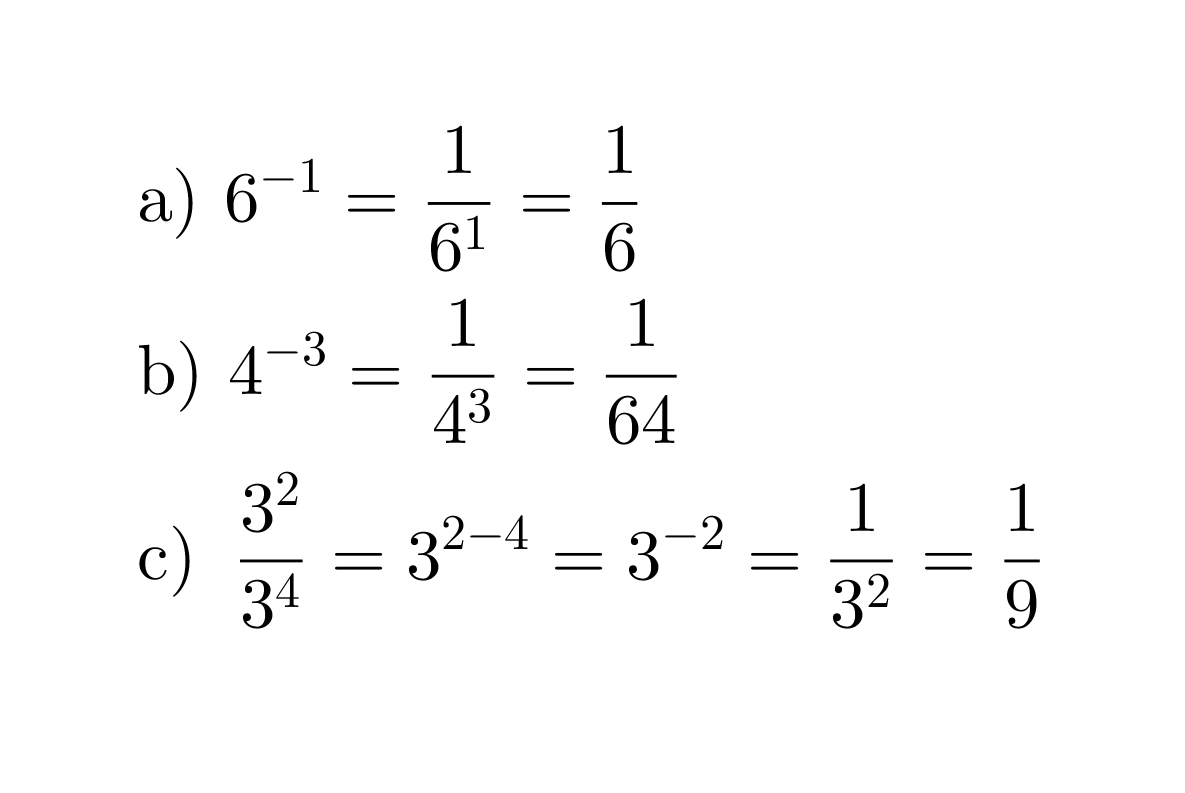
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Kirjoitetaan negatiivisen eksponentin avulla.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Negatiivinen eksponentti
Potenssin negatiivinen eksponentti tarkoittaa kantaluvun käänteisluvun vastaavaa positiivista potenssia.