7. Kymmenpotenssimuoto
Suurten ja pienten lukujen merkitsemisessä käytetään kymmenpotensseja. Kehossamme olevien atomien määrä 4 000 000 000 000 000 000 000 000 000 voidaan esittää lyhyemmin kymmenpotenssimuodossa
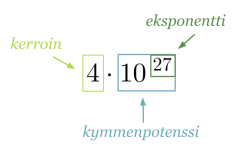
Klikkaa kuva suuremmaksi!
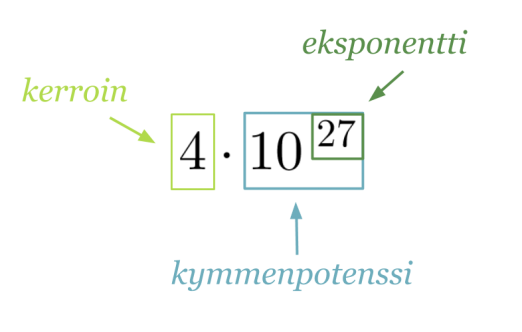
Klikkaa kuva suuremmaksi!
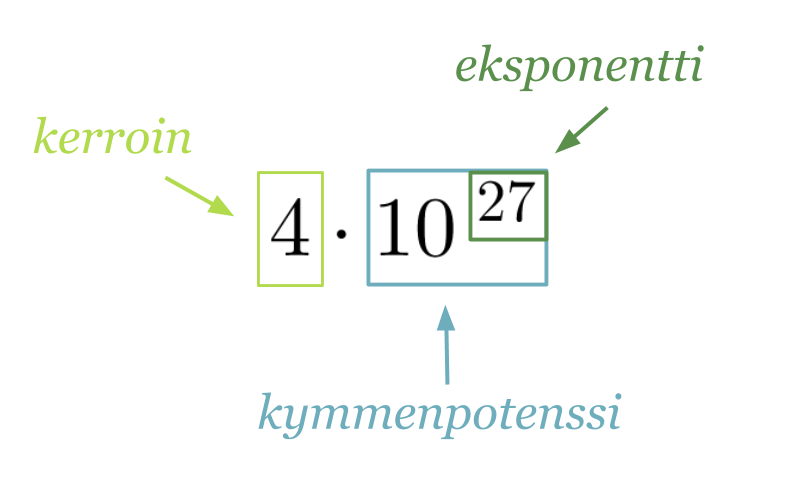
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Lukuja voidaan merkitä
kymmenpotenssimuodossa:
a · 10n,
missä 1 ≤ a < 10 ja n positiivinen tai negatiivinen kokonaisluku.
Esimerkki 1.
Kirjoitetaan luvut normaalimuodossa ilman kymmenpotenssia.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Luku 120 voidaan esittää muodossa 1,2 · 100. Kun kerrotaan sadalla, siirretään desimaalipilkkua kaksi askelta oikealle. Sama luku kymmenpotenssimuodossa on 1,2 · 102.
Luku 0,034 voidaan vastaavasti kirjoittaa muodossa 3,4 · 0,01. Kun kerrotaan sadasosalla, siirretään desimaalipilkkua kaksi askelta vasemmalle. Sama luku kymmenpotenssimuodossa on 3,4 · 10-2.
Esimerkki 2.
Kirjoitetaan luvut kymmenpotenssimuodossa.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Joillakin suurilla luvuilla on omat nimityksensä:
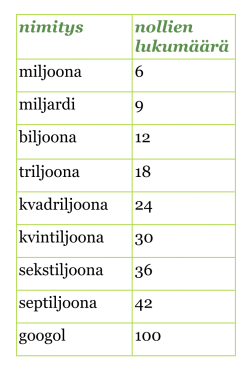
Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!
Huom! Triljoona on Euroopassa 1018, mutta USA:ssa 1012. Vastaavasti biljoona on Euroopassa 1012, mutta USA:ssa 109.
On olemassa myös yleisesti käytettäviä kerrannaisyksiköiden etuliitteitä, joille on valittu omat tunnukset. Eräs tunnetuimmista etuliitteistä on kilo (103). Usein käytetään yleisiä etuliitteitä kymmenpotenssimuotojen sijaan. Tällöin hyväksytään, että kertojaksi tulee myös suurempia lukuja kuin kymmenen ja pienempiä kuin ykkönen. Sanomme mieluummin jonkun massaksi 23 kg kuin 2,3·104 g tai matkan pituudeksi 17 km kuin 1,7·104 m.

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!
Esimerkki 3.
Vesimolekyylin halkaisija on 2,8·10-8. Ilmoita halkaisija
- metreinä
- millimetreinä
- mikrometreinä ja
- nanometreinä.
Ratkaisu:
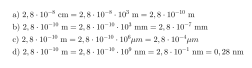
Klikkaa kuva suuremmaksi!
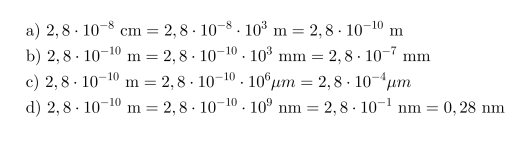
Klikkaa kuva suuremmaksi!
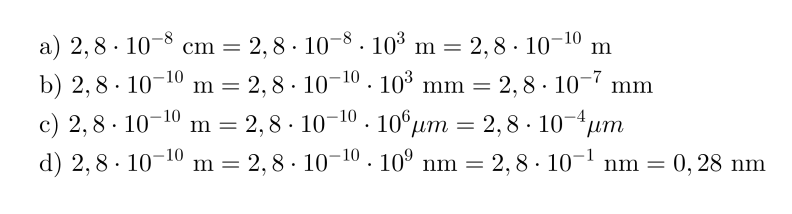
Klikkaa kuva suuremmaksi!
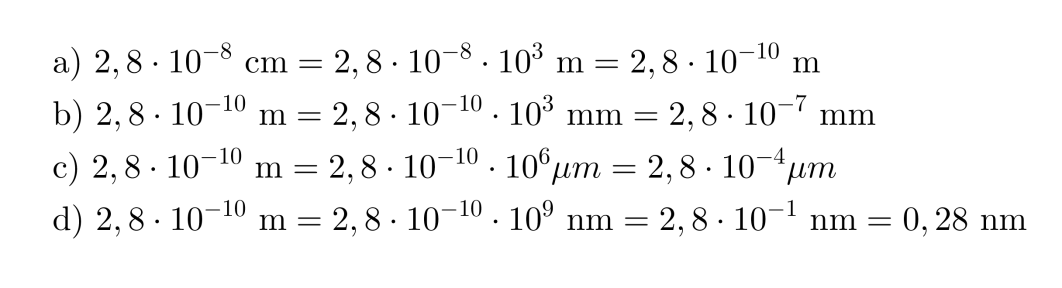
Klikkaa kuva suuremmaksi!
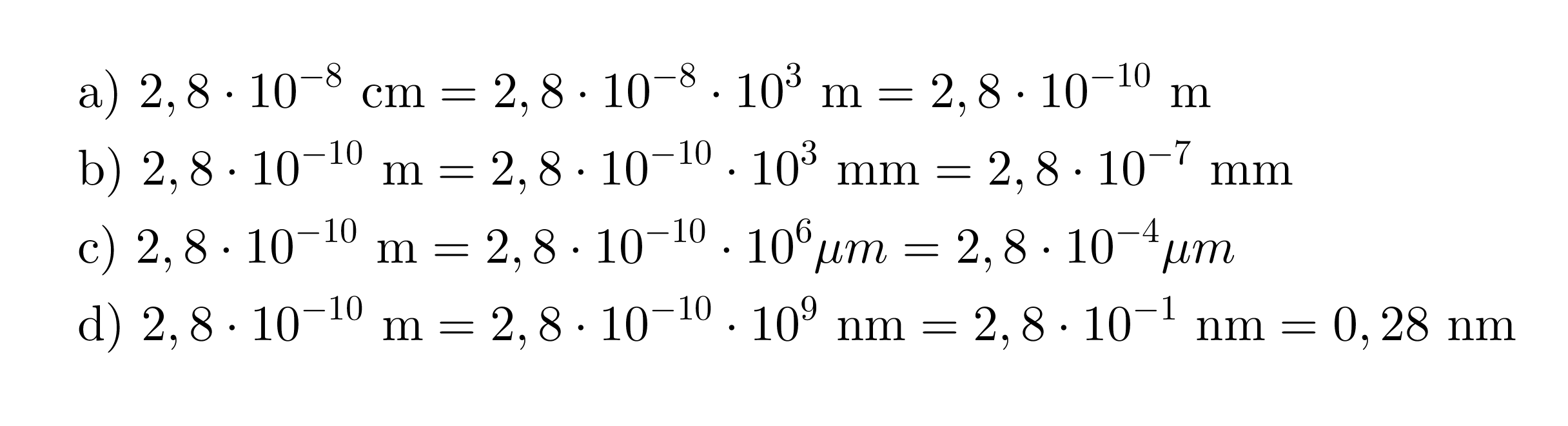
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kymmenpotenssi-
esityksestä normaalimuotoon
Jos luvun kymmenen eksponentti
eksponentin osoittaman määrän
verran.