10. Lausekkeita
Suomessa lämpötilat ilmoitetaan celsiusasteina, mutta esimerkiksi USA:ssa lämpötilojen yhteydessä käytetään fahrenheitasteita. Eri lämpötila-asteikkojen välillä vallitsee tietty yhteys, joka voidaan ilmoittaa matemaattisena lausekkeena. Celsiusasteet voidaan muuttaa fahrenheitasteiksi lausekkeen
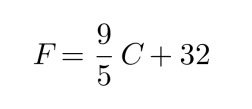
Klikkaa kuva suuremmaksi!
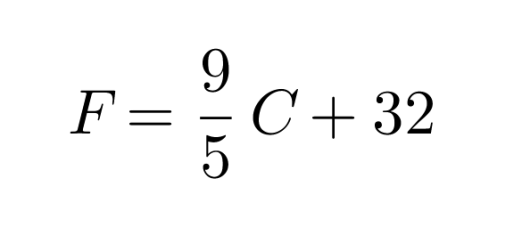
Klikkaa kuva suuremmaksi!
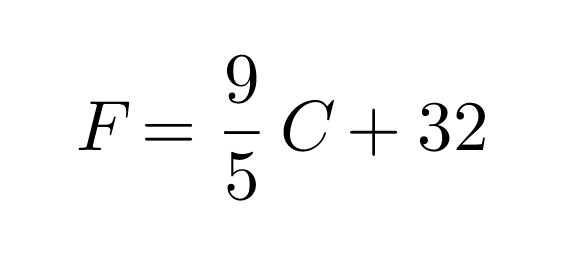
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
avulla, missä F on lämpötila fahrenheitasteina ja C lämpötila celsiusasteina.
Fahrenheitasteiden lauseketta voidaan käyttää yhä uudestaan sijoittamalla C:n paikalle eri lämpötiloja. Tämä on esimerkki muuttujalausekkeesta. Kirjain C edustaa muuttujaa, joka voi saada eri arvoja. Muutttujalausekkeissa kertomerkki jätetään merkitsemättä luvun ja muuttujan tulosa tai useampien muuttujien tulossa. Kertomerkki on ehdottomasti muistettava merkitä, kun muuttujan paikalle sijoitetaan jokin lukuarvo. Lisäksi, jos muuttujan arvo on negatiivinen, on se sijoitettava sulkeissa. Kahta laskutoimitusmerkkiä ei voi esiintyä peräkkäin ilman sulkeita.
Esimerkki 1.
Lasketaan, mitä fahrenheitasteikkoinen lämpötilamittari näyttää, jos lämpotila celsiusasteina on a) 5 °C, b) –15 °C.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: 5 °C on fahrenheitasteina 41 °F ja -15 °C on fahrenheitasteina 5 °F.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kirjaimilla laskeminen voi aluksi tuntua kummalliselta, mutta niiden avulla tosielämän ilmiöistä voidaan tehdä matemaattisia malleja. Yleensä matemaattiset mallit ovat niin monimutkaisia, ettei niiden kuvaamiseen riitä yksi muuttuja. Esimerkiksi maapallon väestonkasvumallissa ovat muuttujina A = väkiluku alussa, t = aika vuosina ja k = kasvukerroin. Väkiluku V, kun on kulunut t vuotta on V = Akt.
Kasvukertoimeen k vaikuttavat monet tekijät, kuten taudit, sodat ja nälänhätä. Siksi sen arvioiminen etukäteen on hankalaa. Tiedetään kuitenkin että maapallon väestönkasvu on hidastumassa, 1960-luvulla kasvukerroin oli 1,02 (tämä tarkoittaa että väestö lisääntyi 2 % vuodessa) ja vuoden 1990 lopussa se oli 1,015. On ennustettu, että vuoteen 2015 mennessä kasvukerroin laskee lukuun 1,01.
Esimerkki 2.
Lasketaan arvio maapallon väkiluvulle 20 vuoden kuluttua, kun tällä hetkellä se on 6,7 miljardia (vuonna 2008). Lasketaan arvio käyttämällä ensin kasvukerrointa 1,015 ja sitten kasvukerrointa 1,01.
Listataan kaikki tehtävässä annetut muuttujat:
A = 6,7 miljardia
k = 1,015
t = 20 vuotta
Sijoitetaan muuttujat lausekkeeseen ja lasketaan lausekkeen arvo:
V = Akt = 6,7·1,01520 ≈ 9,0 miljardia
Lasketaan toinen arvio käyttämällä kasvukerrointa 1,01:
V = Akt = 6,7·1,0120 ≈ 8,2 miljardia
Vastaus: Arvio maapallon väkiluvulle 20 vuoden kuluttua on 9,0 miljardia (kasvukerroin 1,015) tai 8,2 miljardia (kasvukerroin 1,01).
Avoin matematiikka 7Osio 3: Potensseja ja polynomeja28.5.2014
Tyypillisimmät muuttujan arvon sijoitusvirheet