13. Polynomien yhteen- ja vähennyslasku
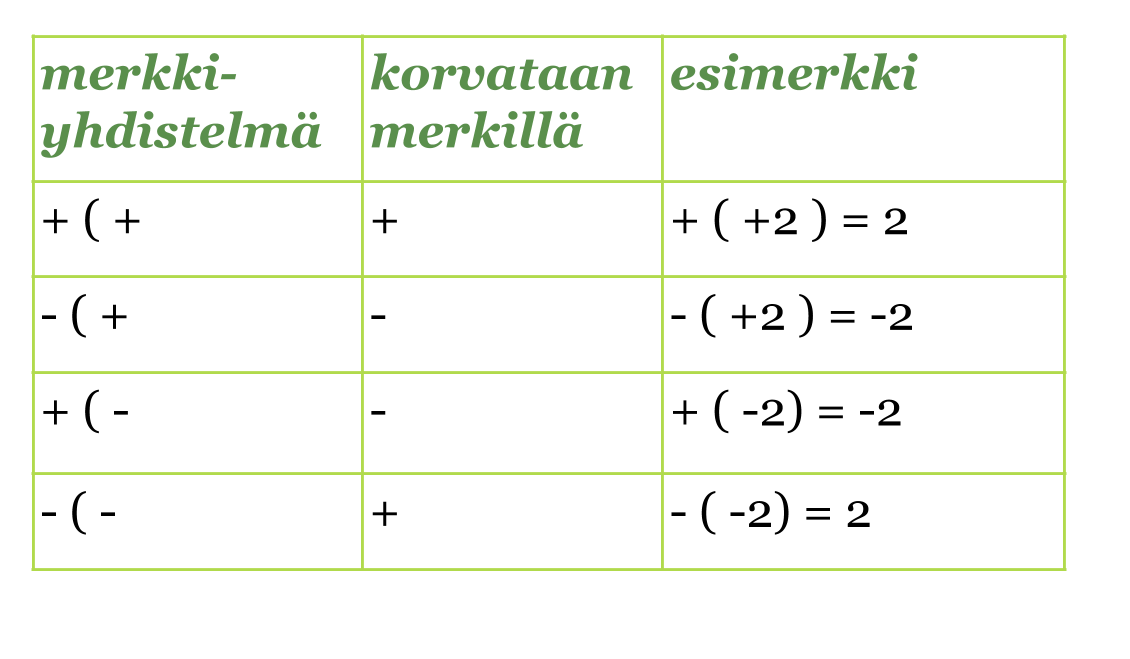
Polynomien yhteen- ja vähennyslaskuissa on oltava tarkkana, kun sulkeita poistetaan. Sulkeiden edessä oleva plusmerkki ei aiheuta muutoksia termien etumerkkeihin, kun sulkeet poistetaan. Jos sulkeiden edessä on miinusmerkki, on kaikkien termien etumerkit vaihdettava vastakkaisiksi sulkeita poistettaessa. Jos et muista, miten kahden etu- ja laskumerkin yhdistelmät korvataan yhdellä merkillä, palauta ne mieleen seuraavasta taulukosta. Nämä on osattava.
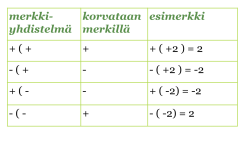
Klikkaa kaavio suuremmaksi!
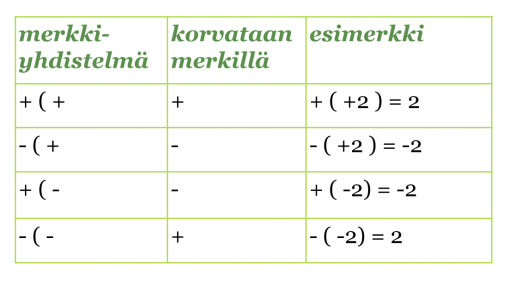
Klikkaa kaavio suuremmaksi!
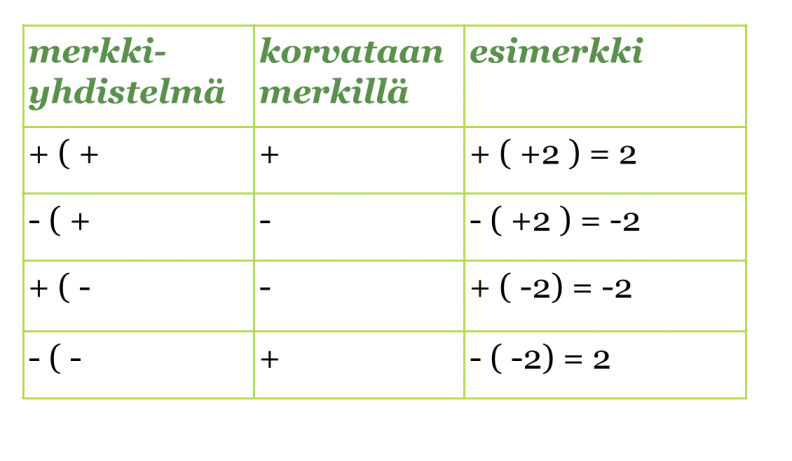
Klikkaa kaavio suuremmaksi!
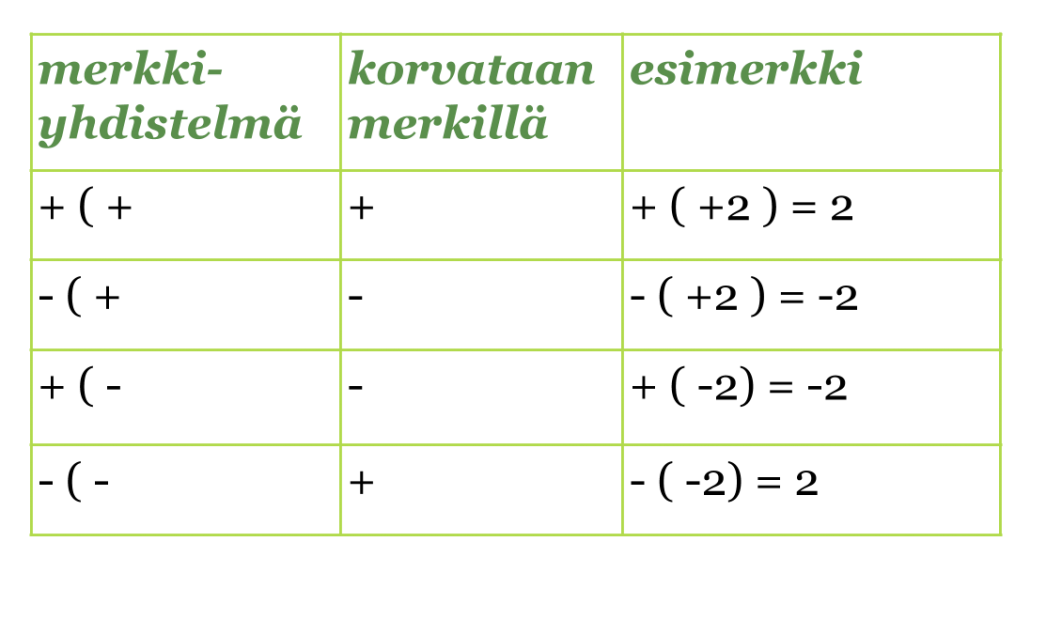
Klikkaa kaavio suuremmaksi!
Klikkaa kaavio suuremmaksi!

Klikkaa kaavio suuremmaksi!
Kahta polynomia, joiden summa on nolla, sanotaan toistensa vastapolynomeiksi. Polynomin vastapolynomi saadaan vaihtamalla polynomin jokaisen termin etumerkki.
Esimerkki 1.
Muodostetaan ja sievennetään polynomien 2a + 3 ja -5a + 1 summa.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Muodostetaan ja sivennetään polynomin -6a2 +b – 1 vastapolynomi.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 3.
Muodostetaan ja sievennetään polynomien 2a + 3 ja -5a +1 erotus.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 4.
Lasketaan polynomin a – 3a2 + 4 – 5a – (3 – 2a2 -4a) arvo, kun a = 10.
Ennen muuttujan arvon sijoittamista, kannattaa polynomi sieventää!
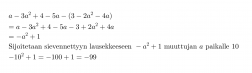
Klikkaa kuva suuremmaksi!
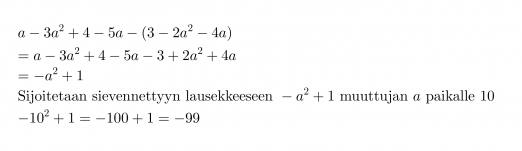
Klikkaa kuva suuremmaksi!
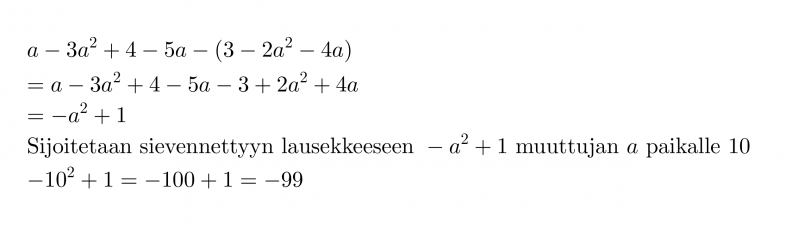
Klikkaa kuva suuremmaksi!
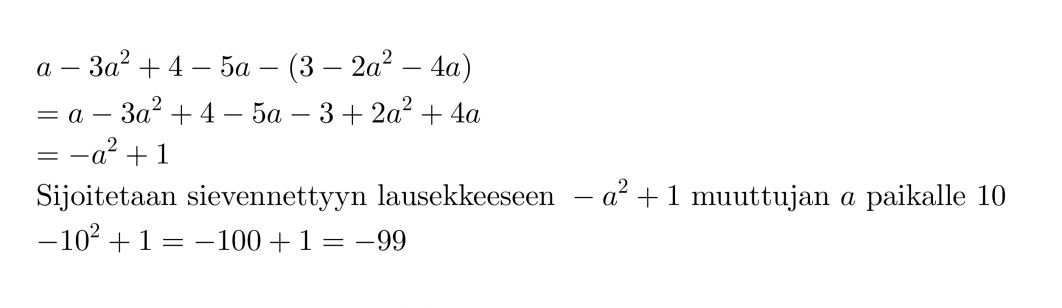
Klikkaa kuva suuremmaksi!
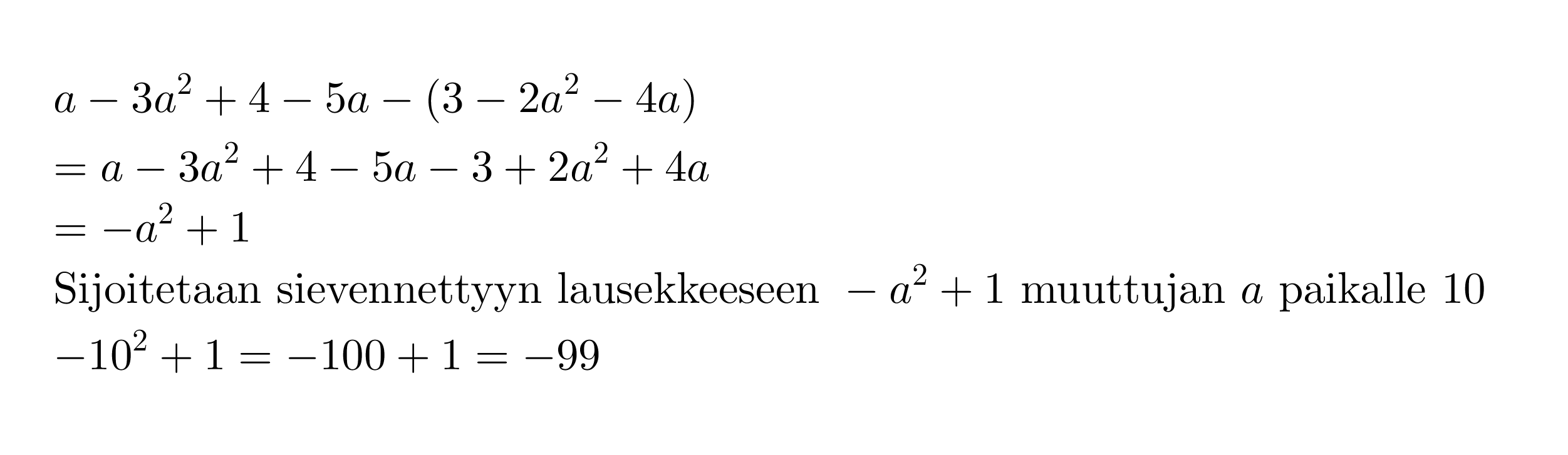
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!