1. Yhtälö

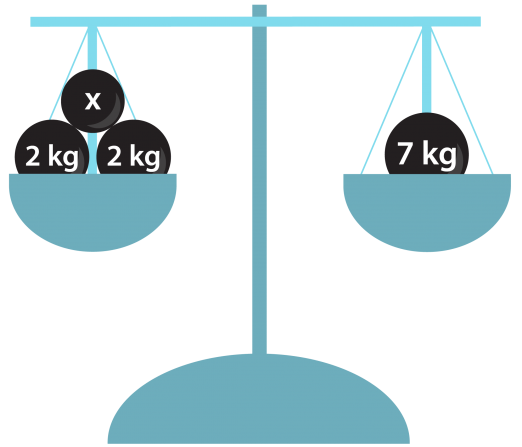
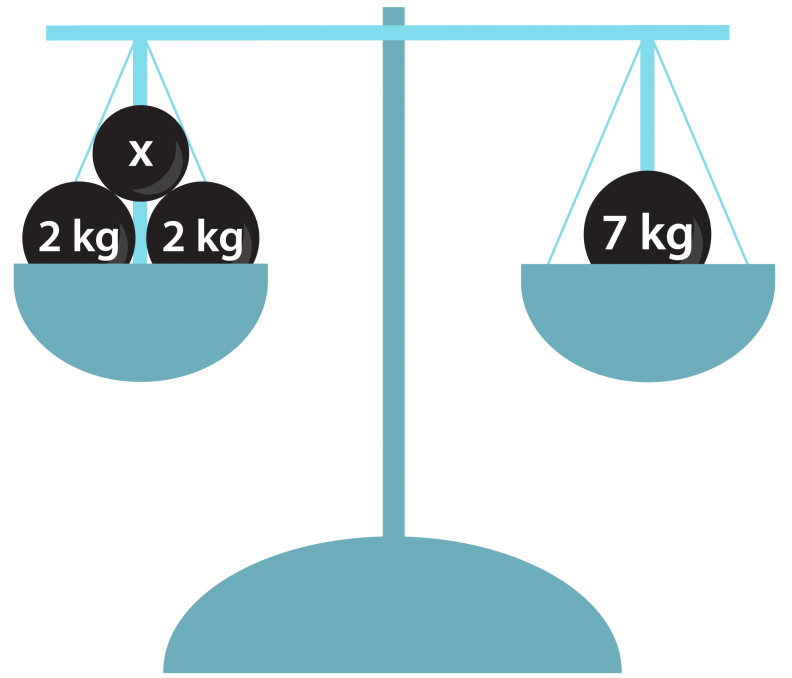
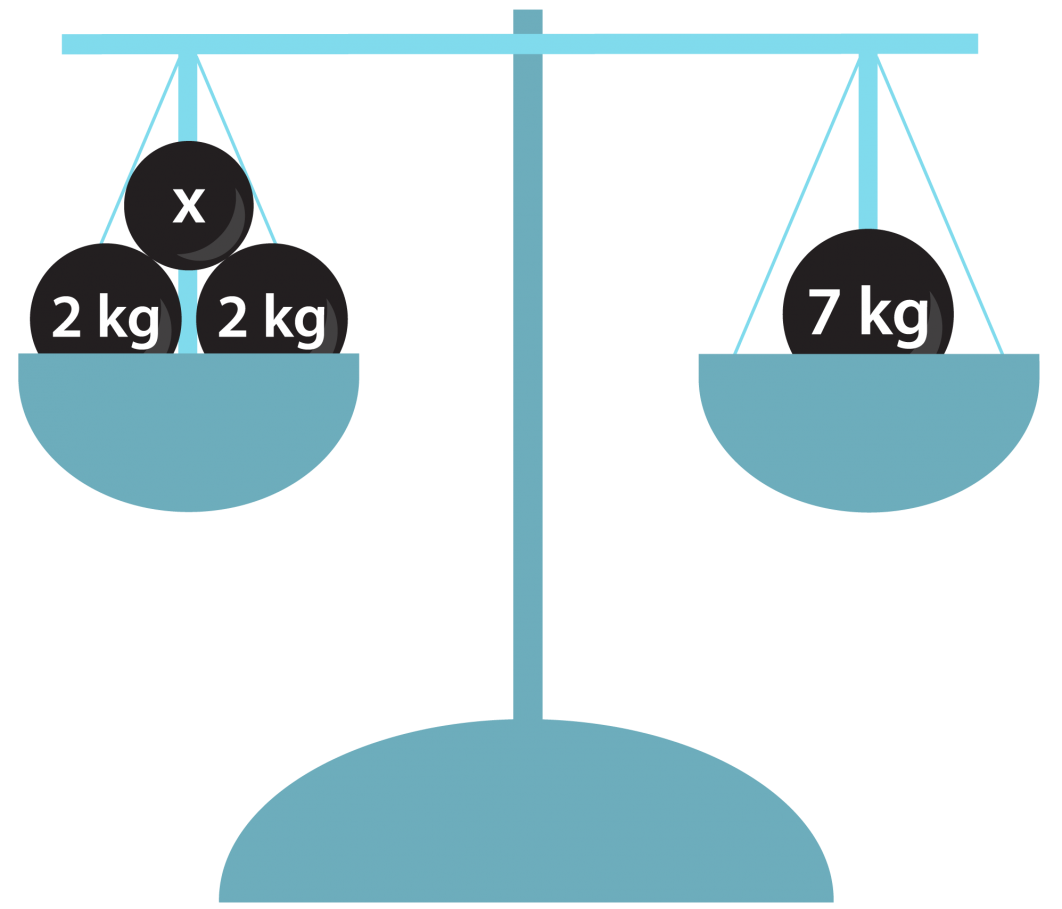
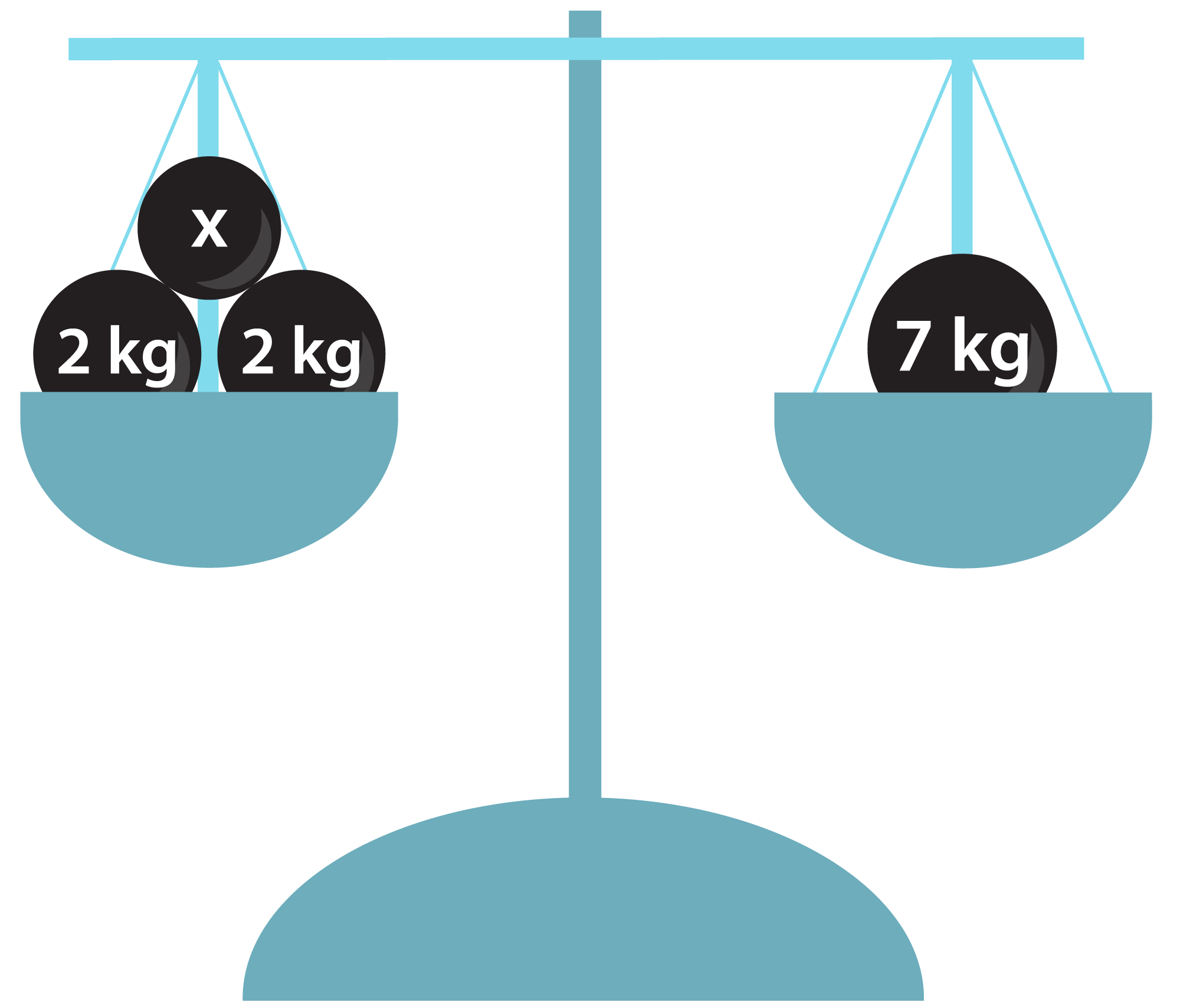
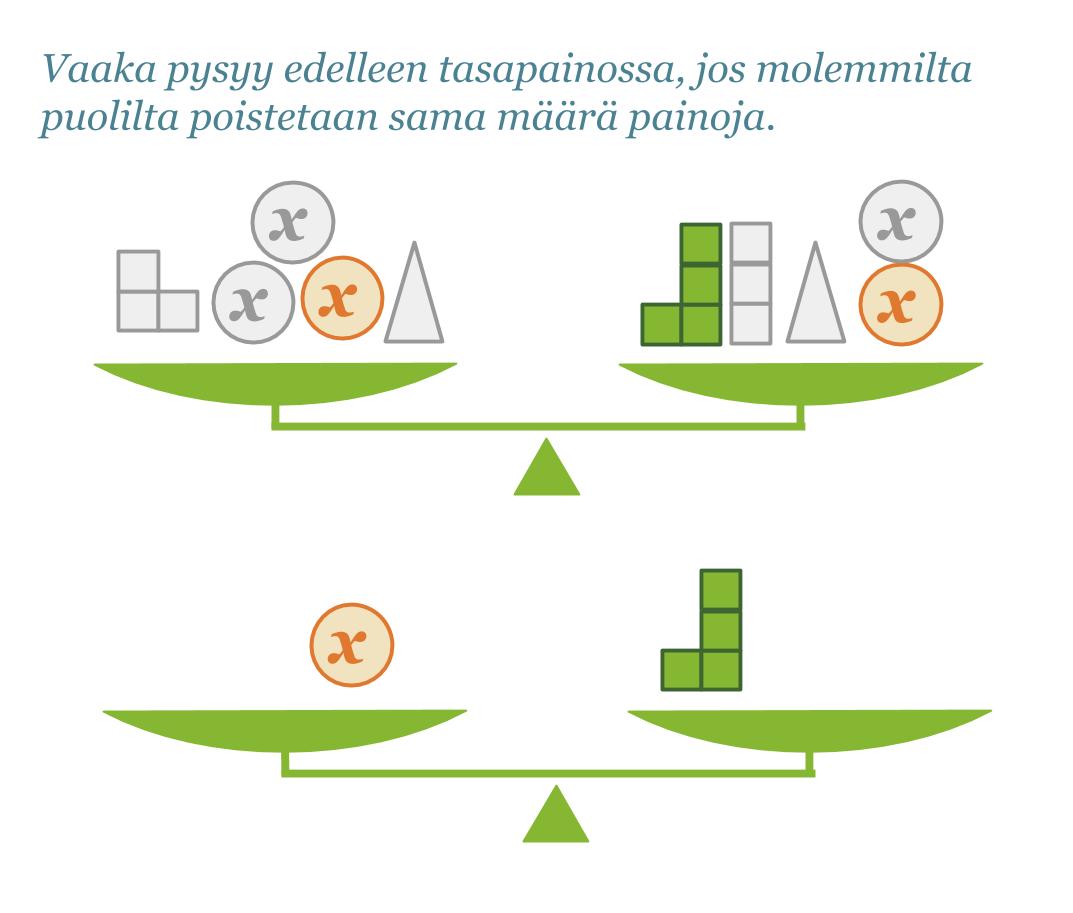
Yh­tä­löä voi­daan ha­vain­nol­lis­taa tasapainovaa’an avul­la. Kun va’an mo­lem­pien puo­lien si­säl­tö pai­naa yhtä pal­jon, vaa­ka on tasa­pai­nos­sa. Vaa­ka säi­lyt­tää tasa­pai­non­sa, jos sen mo­lem­mil­ta puo­lil­ta pois­te­taan tai mo­lem­mil­le puo­lil­le li­sä­tään sa­man­pai­noi­set kap­pa­leet. Myös yh­tä­löl­le voi­daan teh­dä vas­taa­vat toi­men­pi­teet. Jos vaa’an mo­lem­mat puo­let ei­vät pai­na yhtä pal­jon, vaa­ka ei ole tasa­pai­nos­sa. Täl­löin yh­tä­lö­kään ei pidä paik­kaan­sa. Mikä on vaa’an pun­nuk­sen x ol­ta­va, jot­ta yh­tä­lö x + 2 kg + 2 kg = 7 kg oli­si tot­ta?

Klik­kaa kuva suu­rem­mak­si!

Esimerkki 1.

a) 2 + 3 = 5  aina tosi yh­tä­lö

b) 2 · 3 = 10 aina epä­tosi yh­tä­lö

c) x + 5 = 5 eh­dol­li­nen yh­tä­lö, joka to­teu­tuu ai­no­as­taan, kun muut­tu­ja x = 2

Yh­tä­lös­sä ole­vaa muut­tu­jaa ni­mi­te­tään usein tun­te­mat­to­mak­si ja sitä mer­ki­tään ta­val­li­ses­ti x-kir­jai­mel­la. Sii­nä vai­hees­sa, kun yh­tä­löä kir­joi­te­taan, ei tie­de­tä mikä luku tun­te­mat­to­man pai­kal­la pi­täi­si olla, jot­ta yh­tä­lö to­teu­tui­si.

Muut­tu­jan et­si­mis­tä, joka to­teut­taa eh­dol­li­sen yh­tä­lön kut­su­taan yh­tä­lön rat­kai­se­mi­sek­si. Löy­det­tyä muut­tu­jan ar­voa sa­no­taan yh­tä­lön rat­kai­suk­si eli juu­rek­si. Yh­tä­lön rat­kai­su on sel­lai­nen muut­tu­jan arvo, jol­la yh­tä­lön va­sen ja oi­kea puo­li ovat yhtä suu­ret. Yh­tä­lön tyy­pis­tä riip­pu­en sil­lä voi olla yksi tai use­am­pia rat­kai­su­ja tai ei yh­tään rat­kai­sua.

Esimerkki 2.

Tut­ki­taan, to­teut­taa­ko kum­pi­kaan lu­vuis­ta a) x = 1 tai b) x = -2  yh­tä­löä 5x + 1 = -9.

a) Si­joi­te­taan yh­tä­löön x:n pai­kal­le luku 1:

5 · 1 + 1 = 6 ≠ -9

Luku 1 ei to­teu­ta yh­tä­löä.

b) Si­joi­te­taan yh­tä­löön luku –2:

5 · (-2) + 1 = -10 + 1 = -9

Luku -2 to­teut­taa yh­tä­lön.

Esimerkki 3.

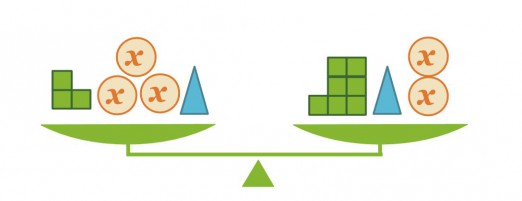
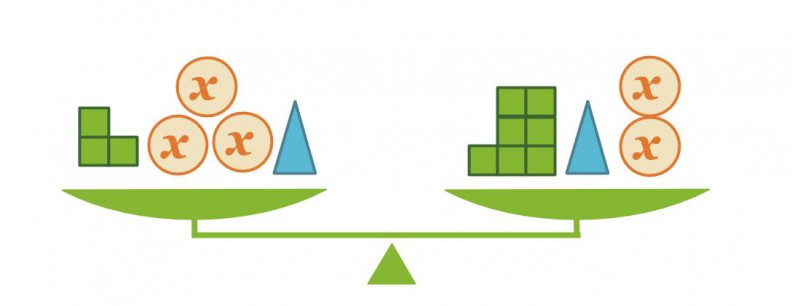
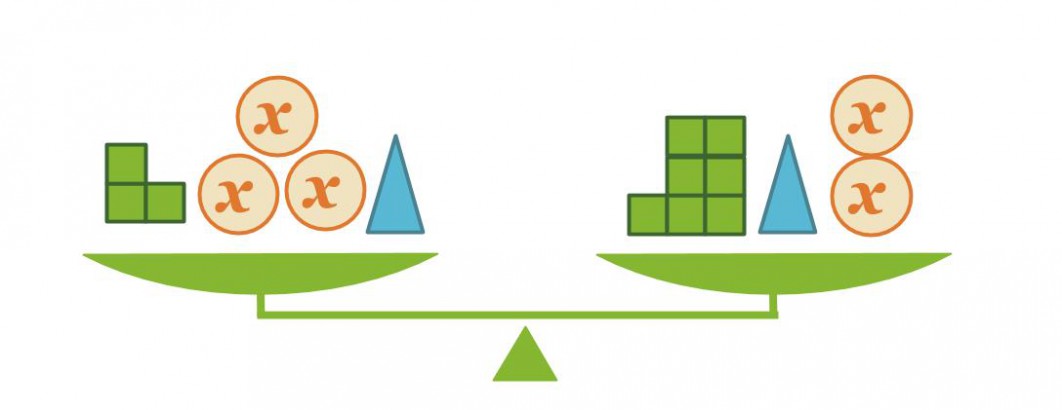
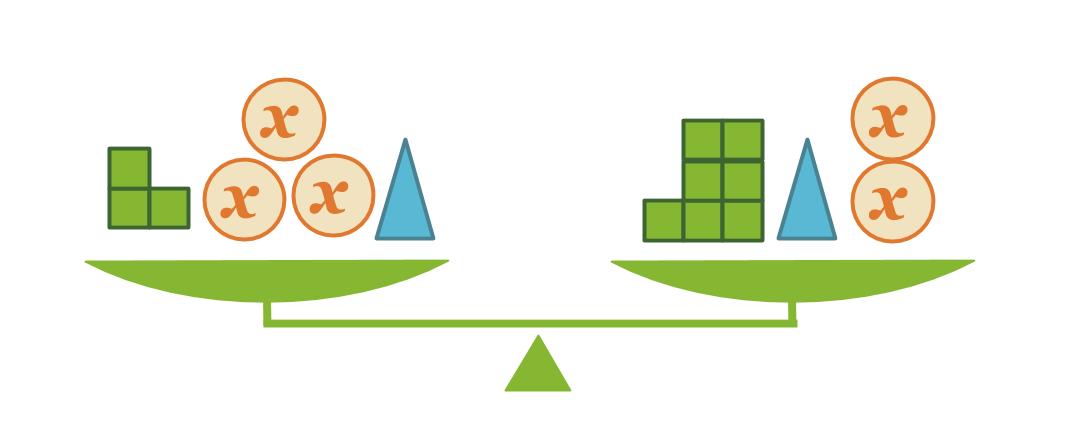
Vaa­ka on tasa­pai­nos­sa. Mikä on x:llä mer­ki­tyn kap­pa­leen mas­sa, kun pie­nen kuu­ti­on mas­sa on 1 kg?

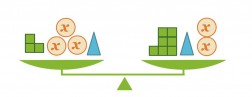
Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

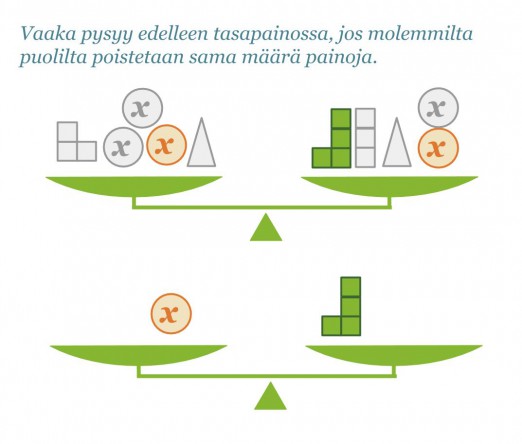
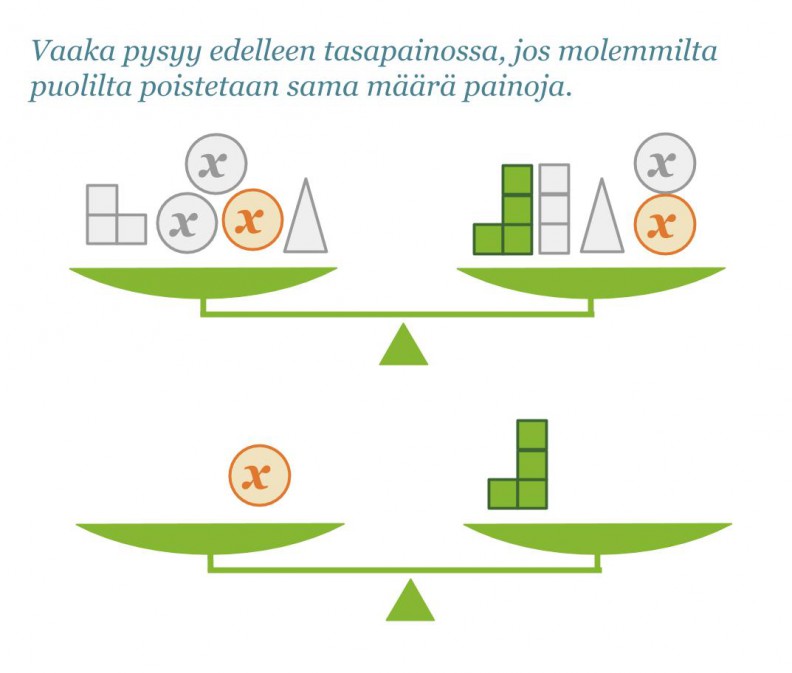
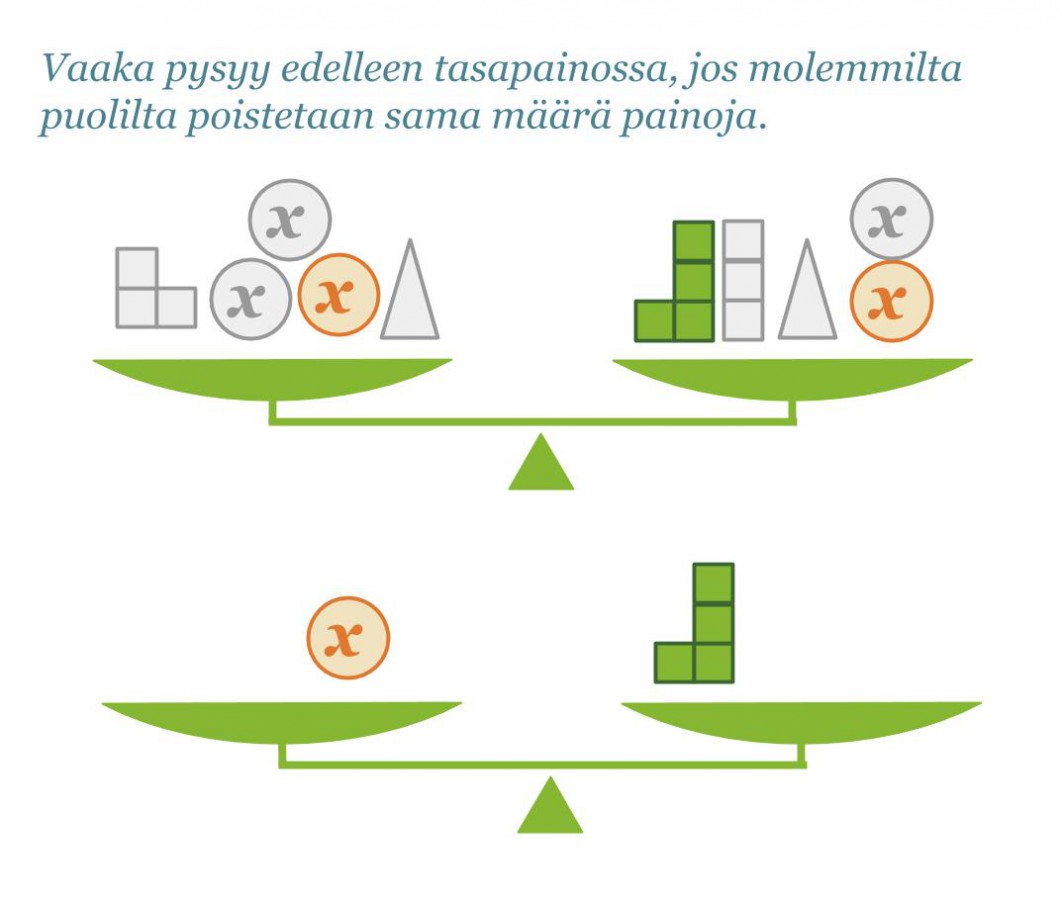
Kir­joi­te­taan ti­lan­tees­ta yh­tä­lö sie­ven­ne­tys­sä muo­dos­sa.

Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Kap­pa­leen x mas­sa on 4 kg.