6. Epäyhtälön ratkaiseminen
Kyseessä on epäyhtälö, kun yhtälössä on yhtäsuuruusmerkin tilalla jokin epäyhtälöä kuvaavista merkeistä:
Jos epäyhtälön molemmille puolille lisätään tai vähennetään sama luku, pitää epäyhtälö edelleen paikkansa. Samoin epäyhtälön molemmat puolet voidaan kertoa tai jakaa puolittain samalla positiivisella luvulla.
Esimerkki 1.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Epäyhtälön ratkaiseminen
Epäyhtälö ratkaistaan samoin kuin tavallinen yhtälö, paitsi kerrottaessa tai jaettaessa negatiivisella luvulla on epäyhtälömerkin suunta vaihdettava.
Esimerkki 3.
Ratkaistaan epäyhtälö 2x > 12.
2x > 12 || :2
x > 6
Tarkistus:
Katsotaan toteuttaako jokin lukua 6 suurempi luku alkuperäisen yhtälön.
2 · 7 > 12
14 > 12 tosi
Esimerkki 4.
Ratkaistaan epäyhtälö x + 2 ≤ 3(x – 2).

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tarkistus:
Valitaan x:n arvoksi esimerkiksi 5.
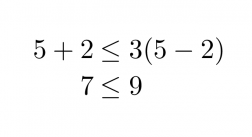
Klikkaa kuva suuremmaksi!
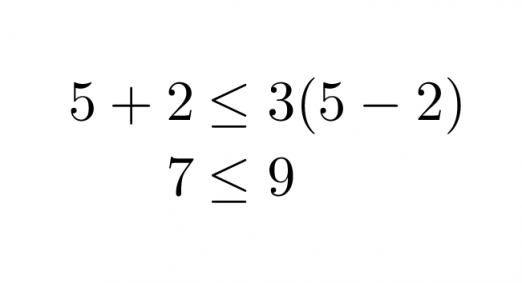
Klikkaa kuva suuremmaksi!
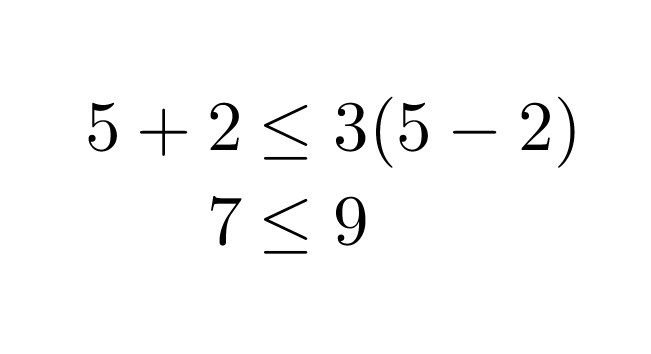
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Epäyhtälöiden merkit
≠ eri suuri kuin
< pienempi kuin
> suurempi kuin
≤ pienempi tai yhtä suuri kuin
≥ suurempi tai yhtä suuri kuin