7. Yhtälöiden ja epäyhtälöiden erikoistapauksia
Kaikilla yhtälöillä ei ole ratkaisua. Lisäksi on olemassa yhtälöitä, jotka pitävät paikkaansa millä x:n arvolla tahansa, tällöin yhtälöllä on äärettömän monta ratkaisua.
Esimerkki 1.
Ratkaistaan yhtälö -x + 2x + 5 = x – 10 + 15.

Klikkaa kuva suuremmaksi!
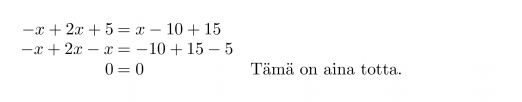
Klikkaa kuva suuremmaksi!
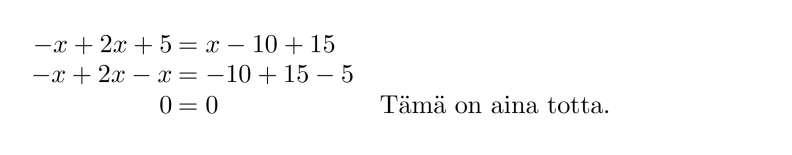
Klikkaa kuva suuremmaksi!
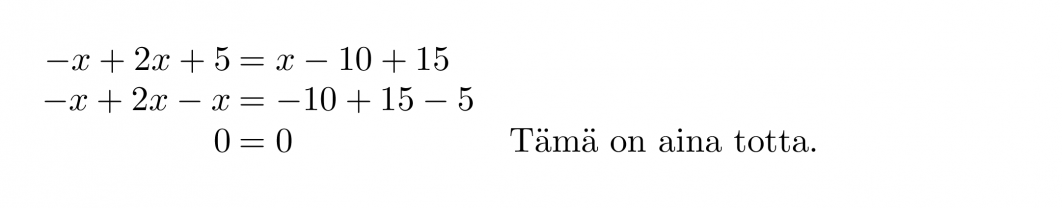
Klikkaa kuva suuremmaksi!
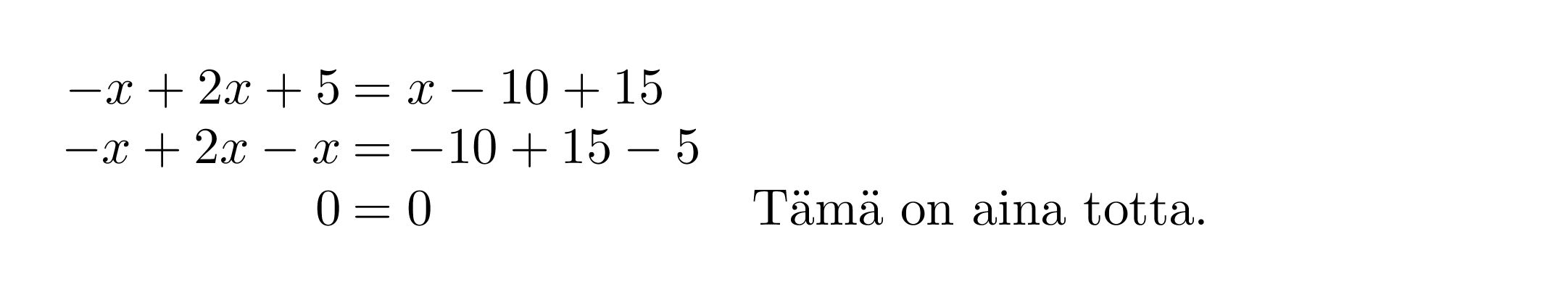
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Yhtälön ratkaisuksi kelpaa mikä tahansa reaaliluku eli yhtälöllä on äärettömän monta ratkaisua.
Esimerkki 2.
Ratkaistaan yhtälö 6x – 4 = 7x – x.

Klikkaa kuva suuremmaksi!
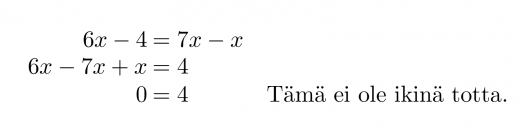
Klikkaa kuva suuremmaksi!
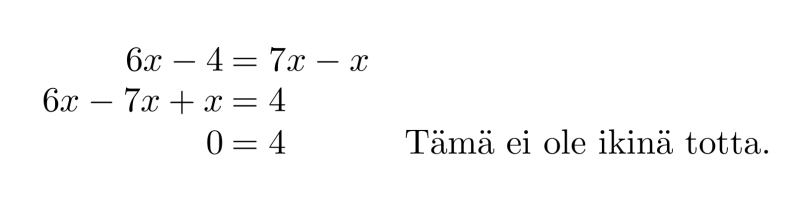
Klikkaa kuva suuremmaksi!
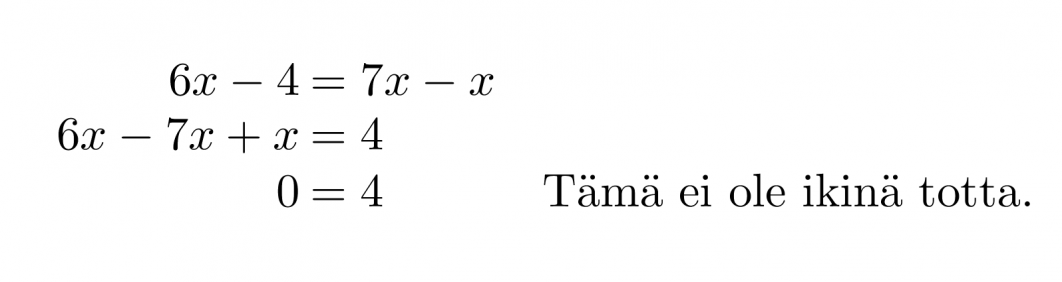
Klikkaa kuva suuremmaksi!
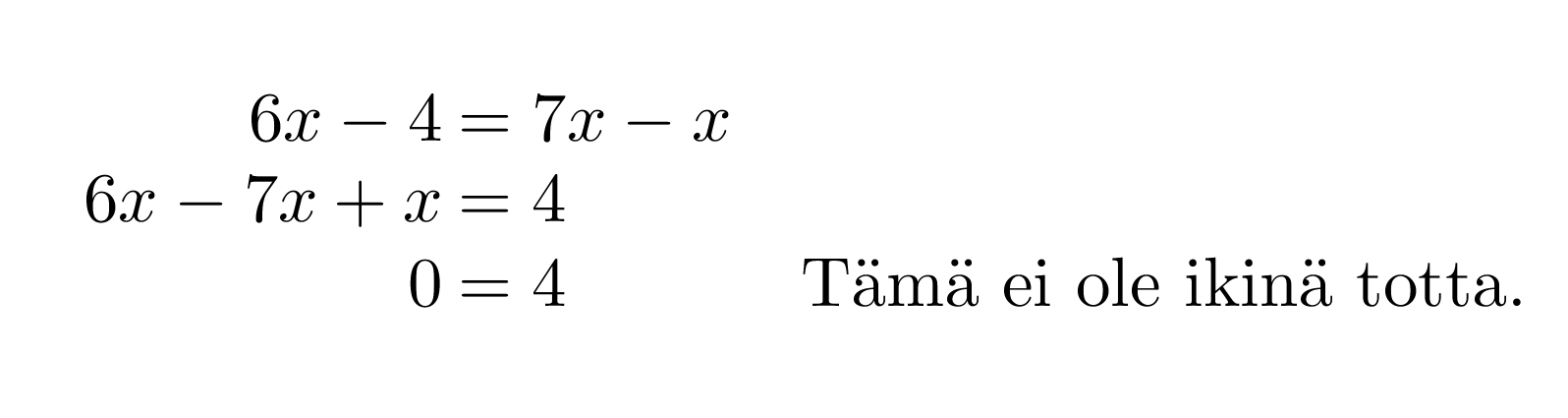
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Yhtälöllä ei ole ratkaisua.
Esimerkki 3.
Ratkaistaan epäyhtälö –2x + 4 ≤ x + 3 – (3x – 1).
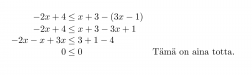
Klikkaa kuva suuremmaksi!
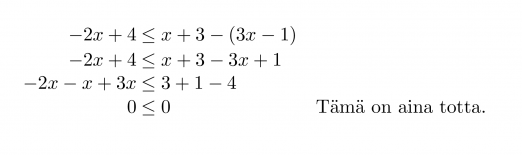
Klikkaa kuva suuremmaksi!
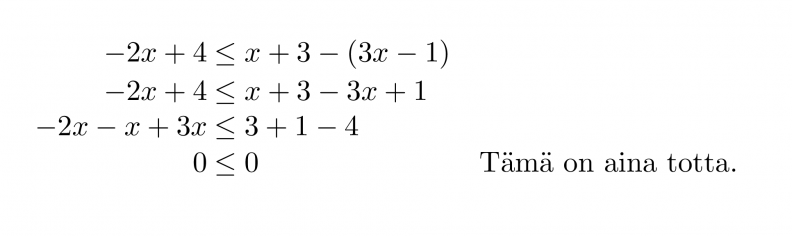
Klikkaa kuva suuremmaksi!
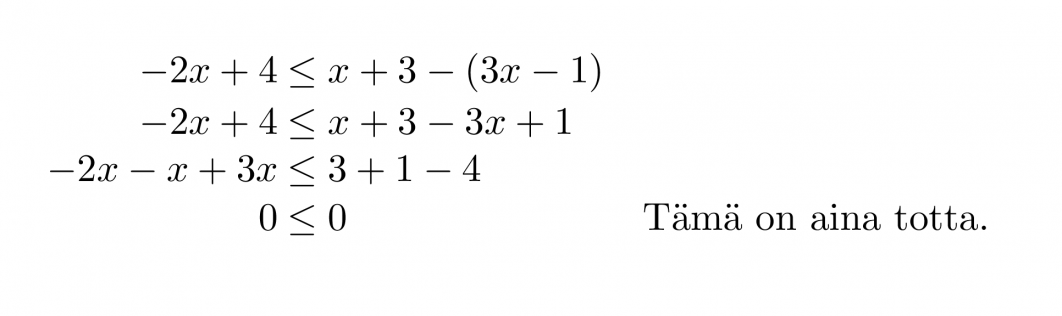
Klikkaa kuva suuremmaksi!
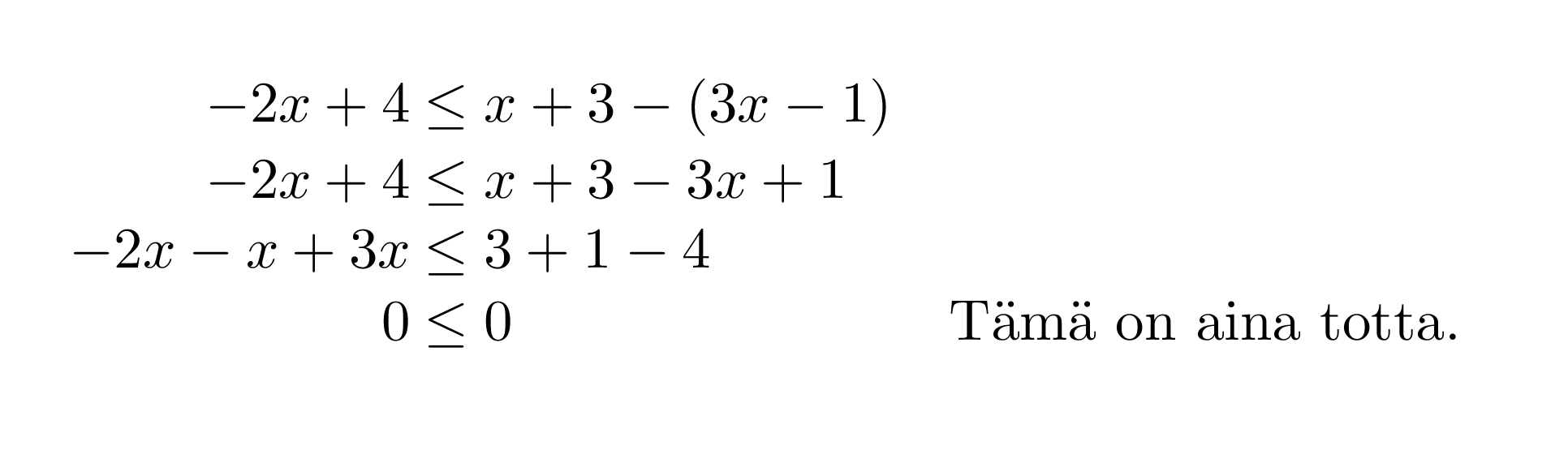
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Epäyhtälön ratkaisuksi kelpaa mikä tahansa reaaliluku eli epäyhtälöllä on äärettömän monta ratkaisua.
Esimerkki 4.
Ratkaistaan epäyhtälö 2(x + 2) ≤ 2x – 1.

Klikkaa kuva suuremmaksi!
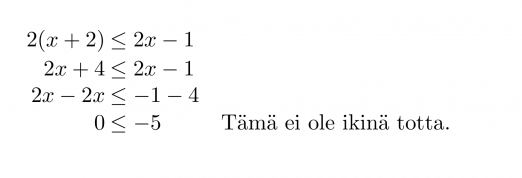
Klikkaa kuva suuremmaksi!
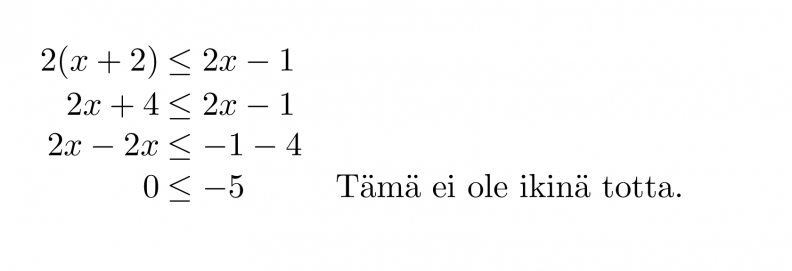
Klikkaa kuva suuremmaksi!
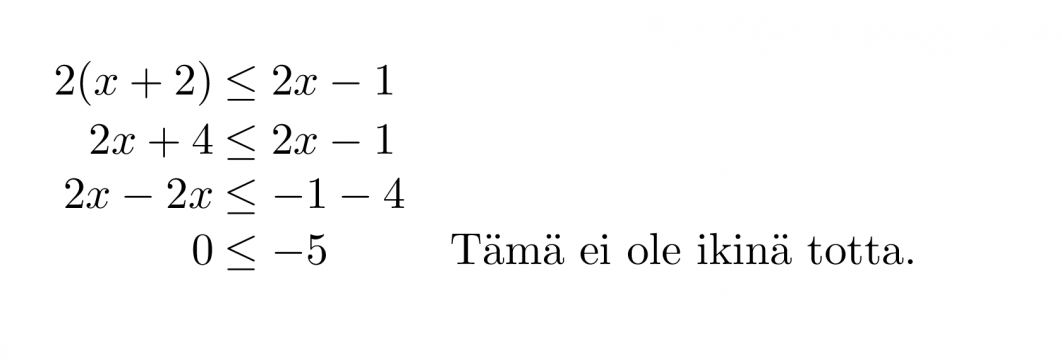
Klikkaa kuva suuremmaksi!
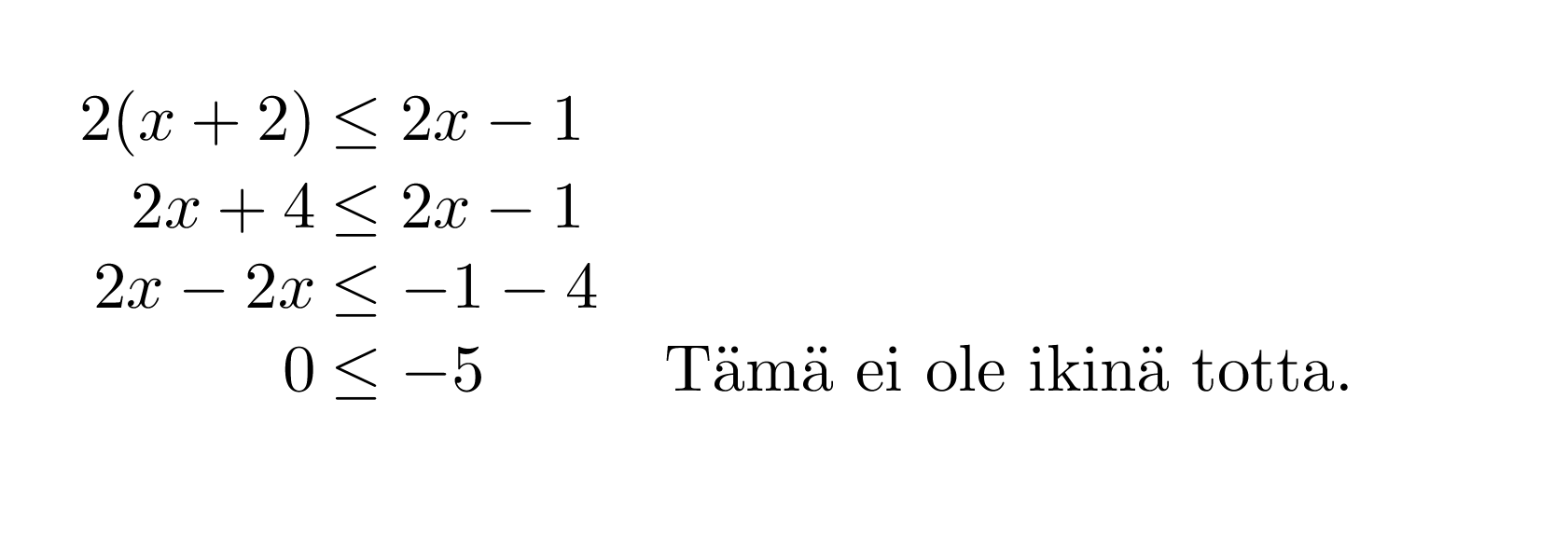
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kyseessä on epätosi epäyhtälö.
Epäyhtälöllä ei ole ratkaisua.
Avoin matematiikka 8Osio 1: Yhtälöitä ja prosentteja4.6.2014