8. Yhtälön muodostaminen sanallisesta ongelmasta

On­gel­ma­teh­tä­vis­tä, jot­ka ete­ne­vät ai­no­as­taan yh­teen suun­taan, sel­vi­tään usein pel­käl­lä päät­te­lyl­lä. Sen si­jaan, jos on­gel­maa on tar­kas­tel­tu kah­des­ta tai use­am­mas­ta eri näkö­kul­mas­ta, vaa­di­taan yh­tä­lön kirjoittamis- ja rat­kai­su­tai­to­ja ti­lan­teen sel­vit­tä­mi­sek­si. Vaik­ka osai­sit pää­tel­lä suo­raan täs­sä kap­pa­lees­sa jon­kin teh­tä­vän, se ei ole sal­lit­tua. On­gel­mis­ta on opit­ta­va muo­dos­ta­maan yh­tä­löi­tä.

Esimerkki 1.

Kun eräs luku ker­ro­taan kol­mel­la ja li­sä­tään tu­loon vii­si, saa­daan 20. Mikä on alku­pe­räi­nen luku?

Ratkaisu:

Mer­ki­tään ky­syt­tyä lu­kua x:llä ja piir­re­tään kaa­vio ti­lan­teen hah­mot­ta­mi­sek­si.

Klik­kaa kuva suu­rem­mak­si!

Kaa­vi­on kaik­ki nuo­let osoit­ta­vat sa­maan suun­taan ja pää­ty­vät lo­pul­ta tu­lok­seen 20. Kaa­vi­on pe­rus­teel­la voi­daan kir­joit­taa yh­tä­lö ja rat­kais­ta se nor­maa­le­ja yh­tä­lön rat­kai­su­sään­tö­jä nou­dat­ta­en.

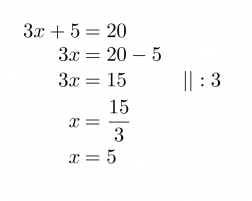
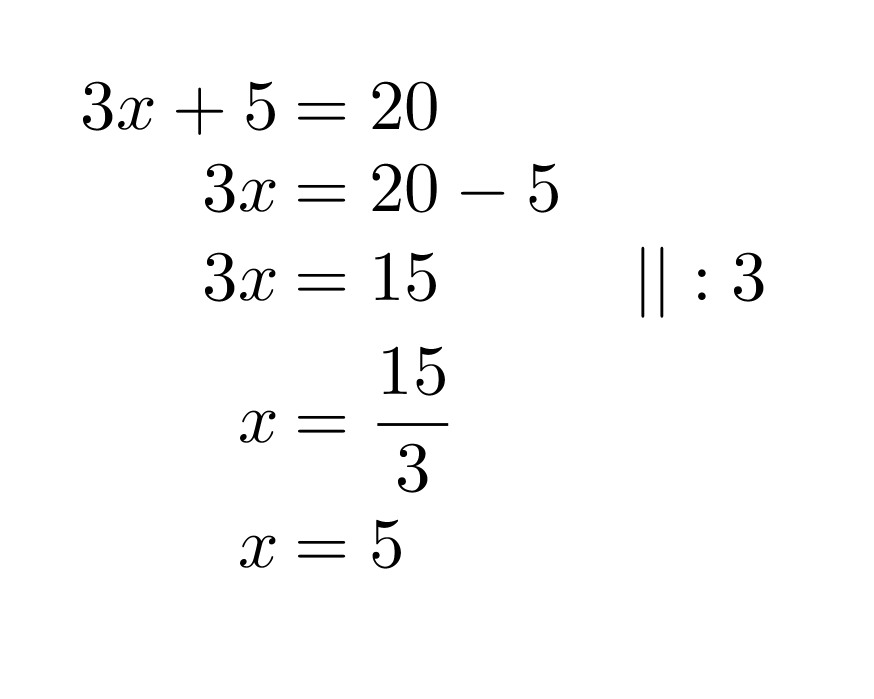
Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Alku­pe­räi­nen luku on 5.

Esimerkki 2.

Kun erää­seen lu­kuun li­sä­tään 6, saa­daan alku­pe­räi­nen luku ne­lin­ker­tai­se­na. Mikä on alku­pe­räi­nen luku?

Ratkaisu:

Mer­ki­tään ky­syt­tyä lu­kua x:llä ja piir­re­tään ti­lan­tees­ta kaa­vio.

Klik­kaa kuva suu­rem­mak­si!

Ky­sees­sä on on­gel­ma, jota tar­kas­tel­laan kah­del­ta eri suun­nal­ta. Mo­lem­mis­sa pää­dy­tään sa­maan lu­kuun, jota ei ole an­net­tu. Kir­joi­te­taan ti­lan­tees­ta yh­tä­lö ja rat­kais­taan se nor­maa­le­ja yh­tä­lön rat­kai­su­sään­tö­jä nou­dat­ta­en.

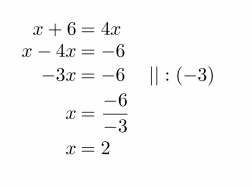
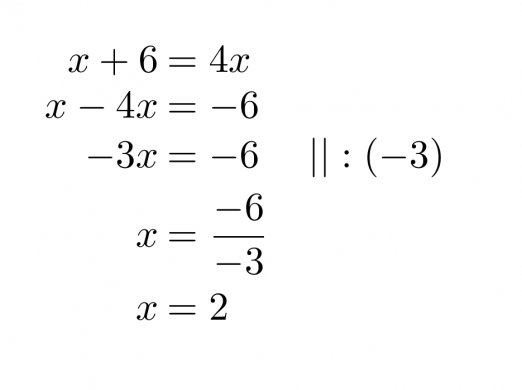
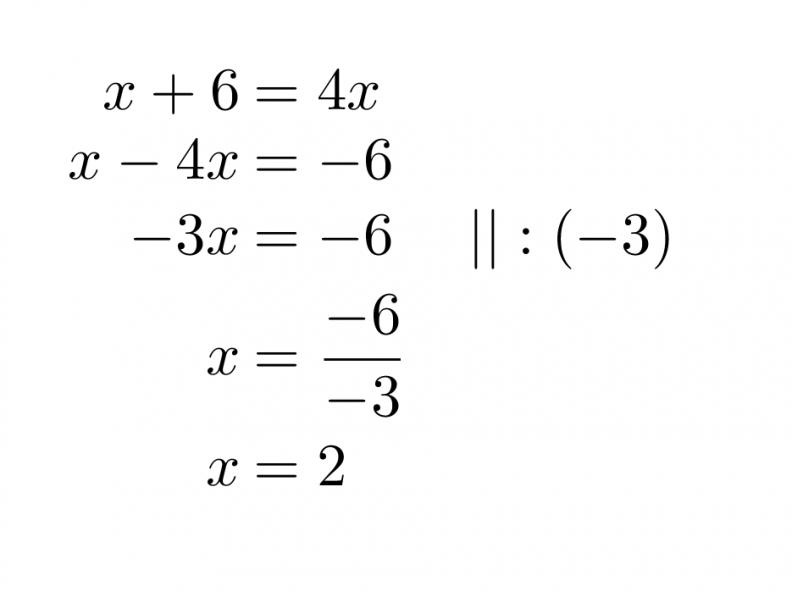
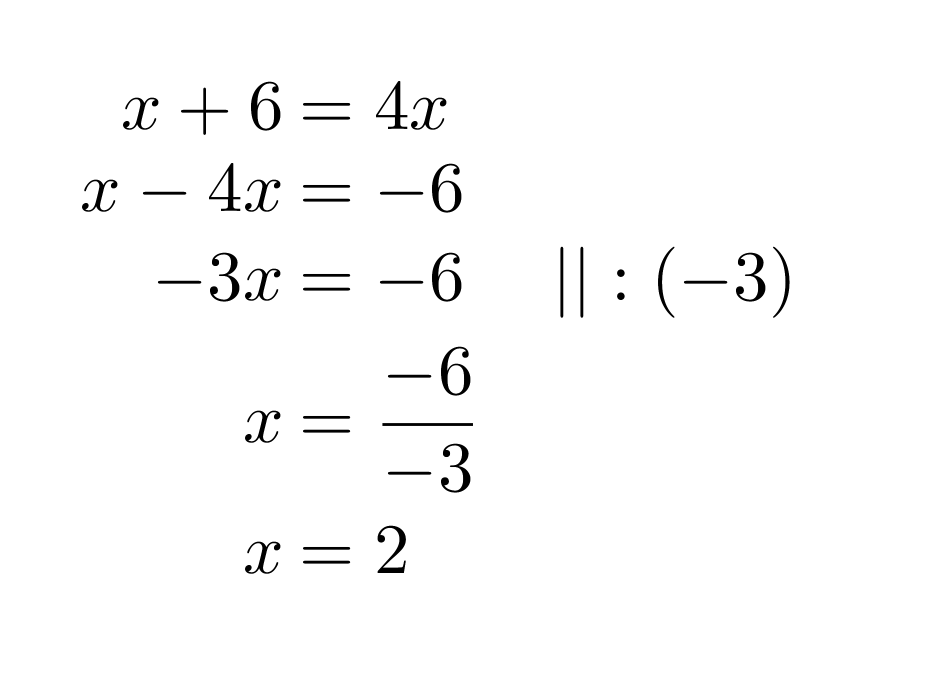
Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Alku­pe­räi­nen luku on 2.