12. Koronkorko
Prosenttilaskussa muutos on hetkellinen eli ajalla ei ole merkitystä, mutta korkolaskussa huomioidaan myös aika. Alkuperäinen luku kasvaa tietyn prosentin mukaan, mutta lisäyksen suuruus riippuu ajasta.
Korkoaika: Euroopan keskuspankki käyttää korkovuoden pituutena 360 päivää. Jos tehtävissä ei ole annettu päivämääriä, käytä korkoaikoja 1 vuosi = 12 kuukautta = 52 viikkoa = 360 päivää.
Esimerkki 1.
Pankkitilin vuotuinen korko on 2 %. Lasketaan, kuinka suureksi 1000 € talletus kasvaa kahdeksassa vuodessa?
Kyseessä on lisäys prosentteina, joten laskutoimitus suoritetaan, kuten edellisessä kappaleessa opittiin.
talletus 1. vuoden jälkeen:
1,02 · 1000 € = 1020 €
talletus 2. vuoden jälkeen:
1,02 · 1020 € = 1,02 · 1,02 · 1000 € = 1,022 € · 1000 € = 1040,4 €
talletus 3. vuoden jälkeen:
1,02 · 1040,4 € = 1,02 · 1,02 · 1,02 · 1000 € = 1,023 · 1000 € = 1061,208 €
Edellisen perusteella nähdään, että
talletus 8. vuoden jälkeen:
1,028 · 1000 € ≈ 1174,66 €

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Paljonko korkoa kertyy 15 000 euron talletukselle kymmenessä vuodessa, jossa säästötilin vuotuinen korko on 1,7 %?
Lasketaan ensin paljonko on talletuksen arvo kymmenen vuoden kuluttua:
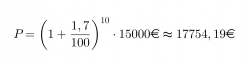
Klikkaa kuva suuremmaksi!
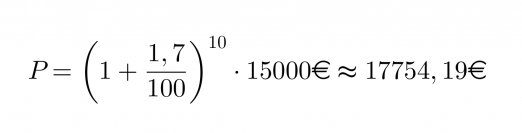
Klikkaa kuva suuremmaksi!
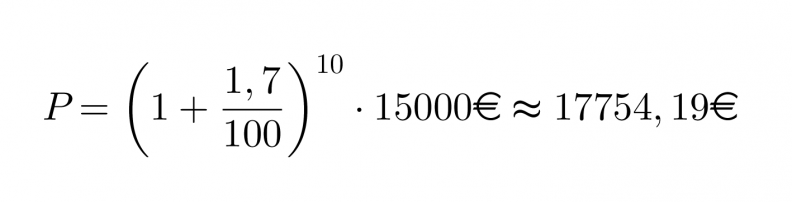
Klikkaa kuva suuremmaksi!
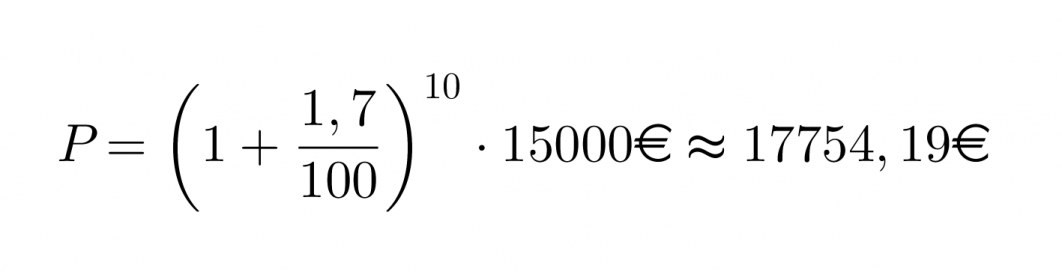
Klikkaa kuva suuremmaksi!
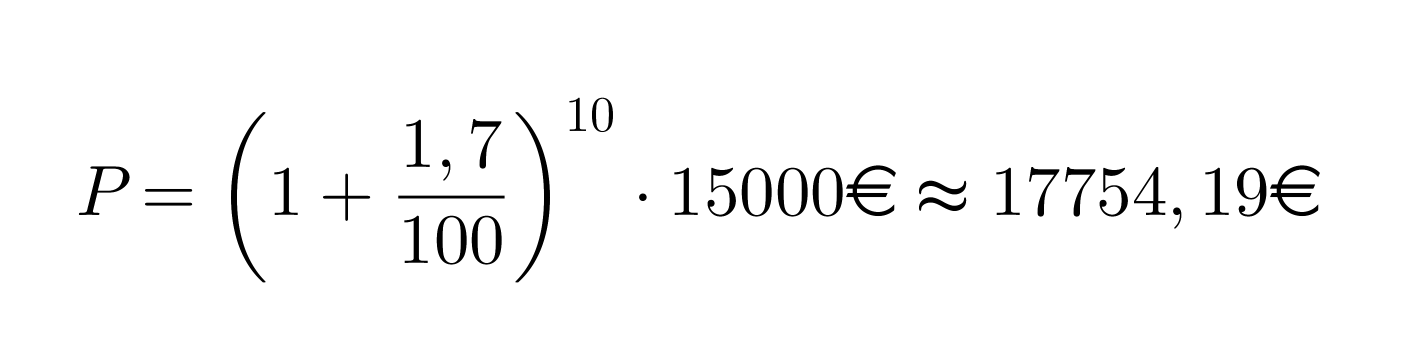
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Koron osuus saadaan vähennyslaskulla:
17754,19€ – 15000€ = 2754,19€
Esimerkki 3.
Freda- täti jätti Tealle perinnöksi 118022,23 € talletuksen, jotka oli sijoitettu kymmeneksi vuodeksi 12 % vuosikorolla. Paljonko talletuksen arvo oli alunperin?
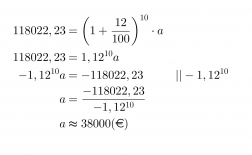
Klikkaa kuva suuremmaksi!
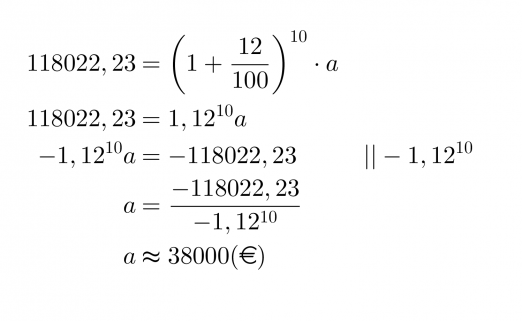
Klikkaa kuva suuremmaksi!
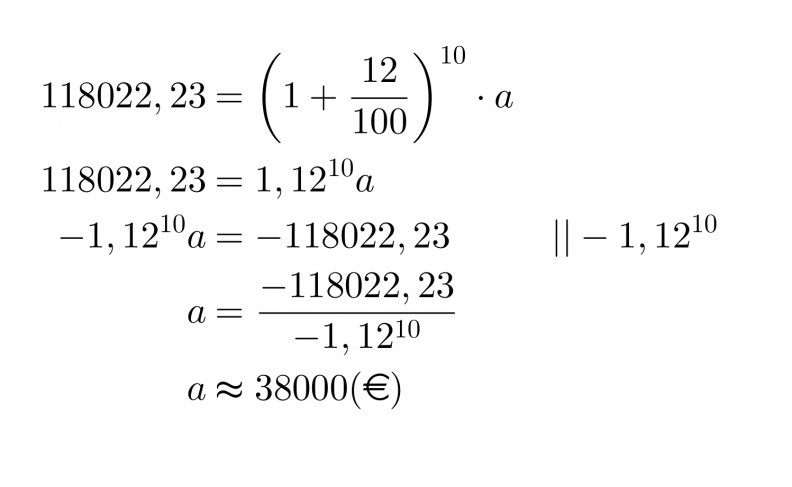
Klikkaa kuva suuremmaksi!
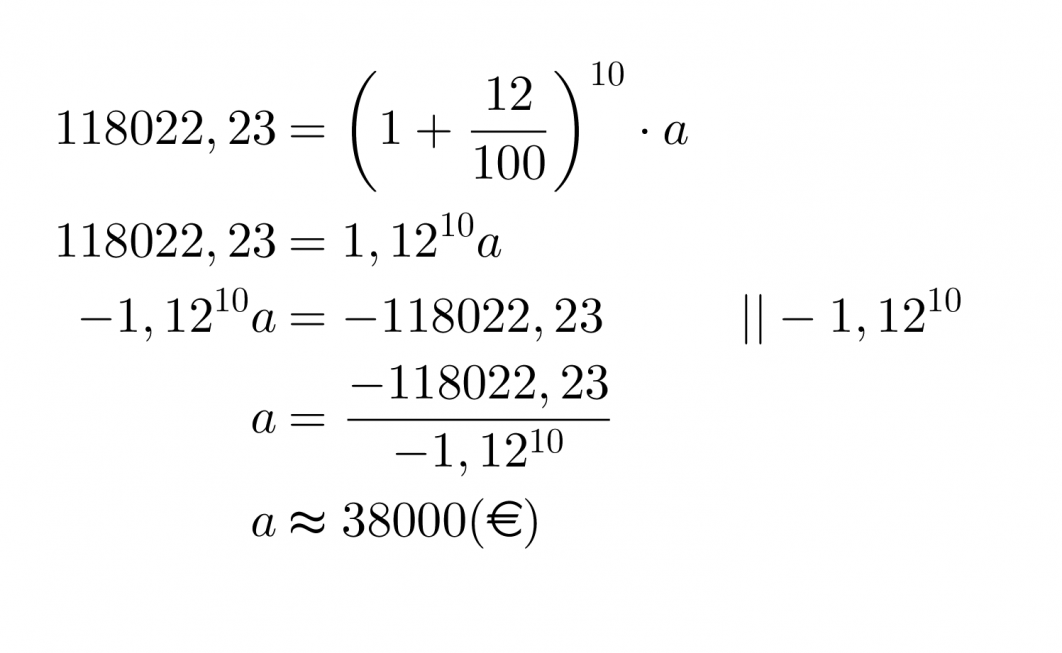
Klikkaa kuva suuremmaksi!
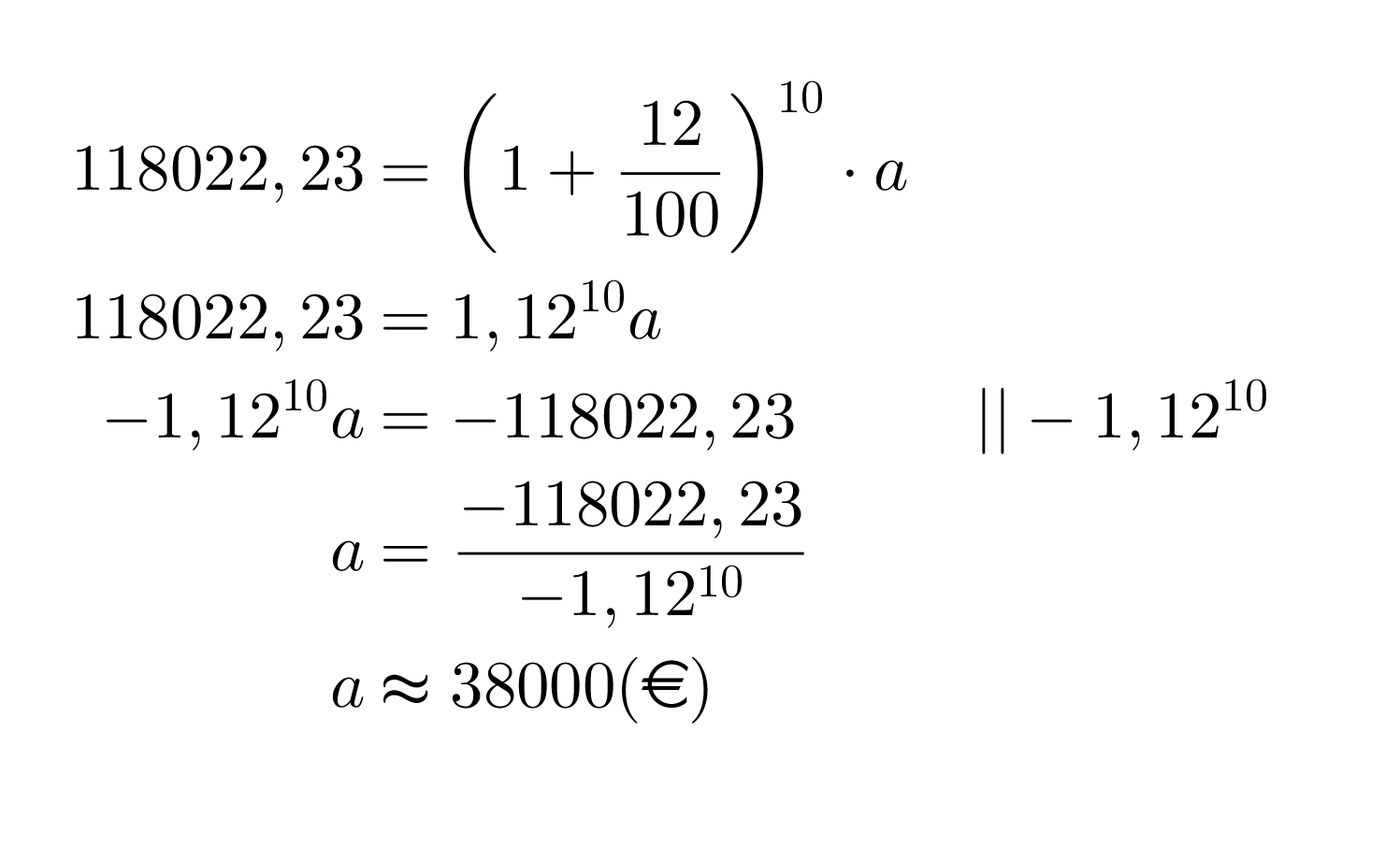
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus
Talletuksen arvo oli alunperin noin 38 tuhatta euroa.
Avoin matematiikka 8Osio 1: Yhtälöitä ja prosentteja4.6.2014
Pääoma n vuoden jälkeen