14. Tuntematon perusarvo
Prosenttilaskennassa on oltava tarkkana siitä, mikä on perusarvo, johon prosentuaalinen muutos kohdistuu. Luvun muuttuessa useita kertoja peräkkäin on perusarvona kulloinkin muutoksen kohteena ollut arvo. Joissakin tehtävissä perusarvo ei ole tiedossa, tällöin sitä merkitään jollakin kirjainvakiolla ja laskut suoritetaan muuten tavalliseen tapaan.
Esimerkki 1.
Mistä luvusta 20 % on 37?

Klikkaaa kuva suuremmaksi!

Klikkaaa kuva suuremmaksi!

Klikkaaa kuva suuremmaksi!

Klikkaaa kuva suuremmaksi!

Klikkaaa kuva suuremmaksi!

Klikkaaa kuva suuremmaksi!
Esimerkki 2.
Mirkalla on rahoistaan 15 % lompakossa ja loput pankkitilillä. Lompakossa hänellä on 105 €. Paljonko Mirkalla on rahaa tilillä?
Ratkaisu:
Prosenttikerroin on 0,15 ja prosenttiarvo 105 €. Ennen kuin lasketaan Mirkan tilillä olevat rahat, lasketaan paljonko hänellä on kaiken kaikkiaan rahaa eli mikä on perusarvo a.
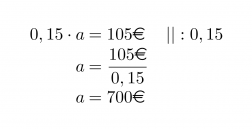
Klikkaa kuva suuremmaksi!
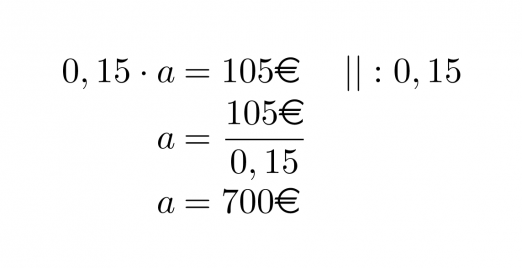
Klikkaa kuva suuremmaksi!
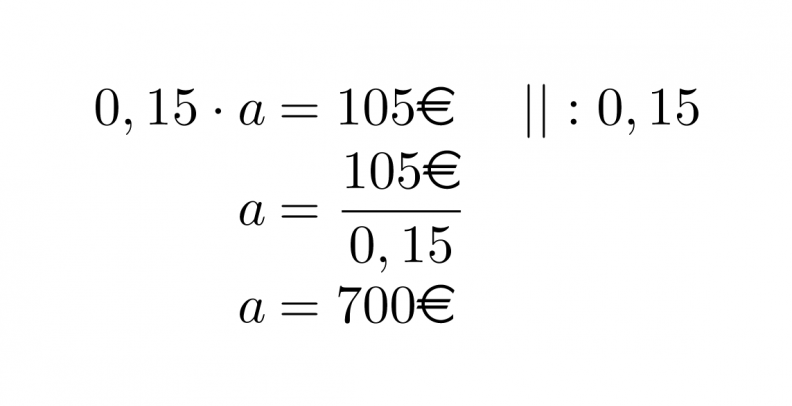
Klikkaa kuva suuremmaksi!
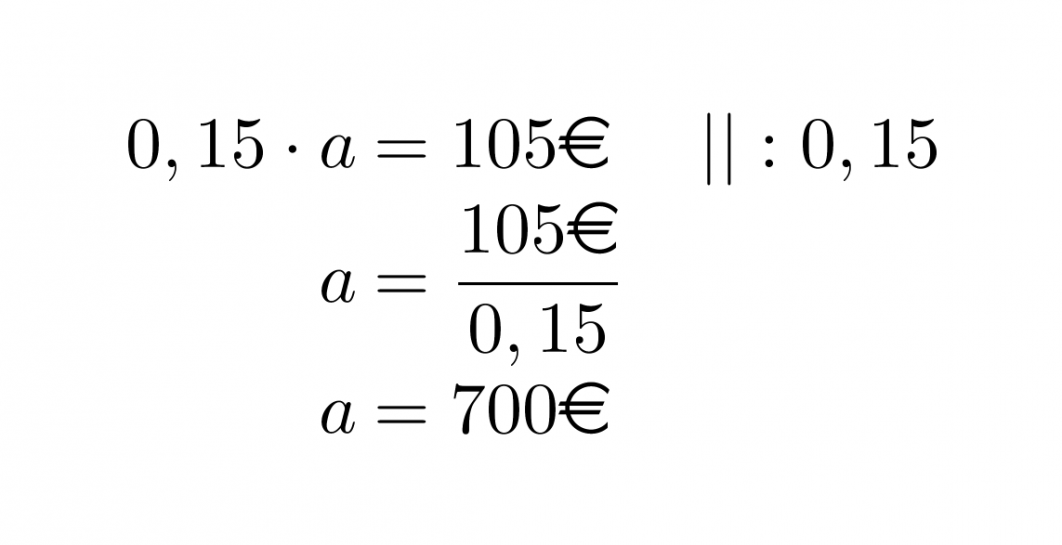
Klikkaa kuva suuremmaksi!
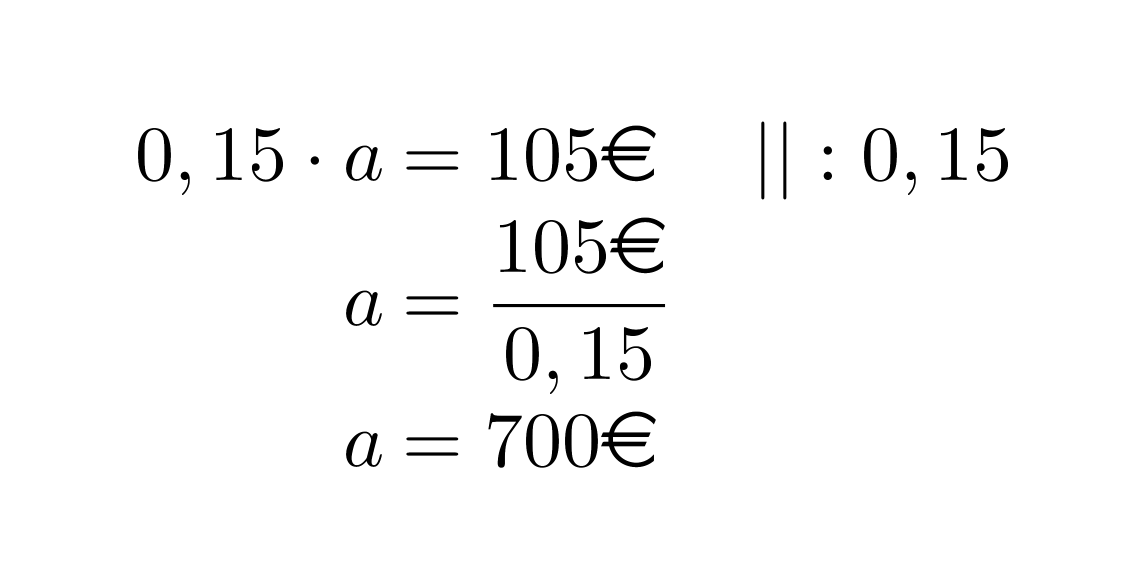
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Mirkalla on tilillä 100 % – 15 % = 85 % kaikista rahoista.
0,85 · 700€ = 595€.
Vastaus: Mirkalla on tilillä 595 €.
Esimerkki 3.
Tietokoneen hintaa alennettiin ensin 10 % ja myöhemmin vielä 15 %. Alennuksen jälkeen tietokone maksoi 1071 €. Paljonko tietokone maksoi alun perin?
Ratkaisu:
Merkitään tietokoneen alkuperäistä hintaa x:llä ja muodostetaan yhtälö.
10 % halvempi tuotteen hinta saadaan kertomalla alkuperäinen hinta luvulla 0,9 ja vastaavasti 15 % lisäalennus huomioidaan kertomalla edellinen hinta luvulla 0,85.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Tietokoneen hinta ennen alennusta oli 1400 €.
Esimerkki 4.
Lukuun lisätään ensin 25 % ja sitten siitä vähennetään 50 %. Montako prosenttia saatu luku on alkuperäisestä luvusta?
Ratkaisu:
Perusarvoa eli alkuperäistä lukua ei nyt tunneta, joten merkitään sitä kirjaimella a.
25 % korotus saadaan voimaan kertomalla perusarvo luvulla 1,25 ja 50 % lisävähennys huomioidaan kertomalla muuttunut perusarvo luvulla 0,50.
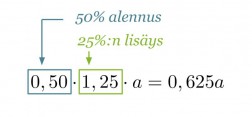
Klikkaa kuva suuremmaksi!
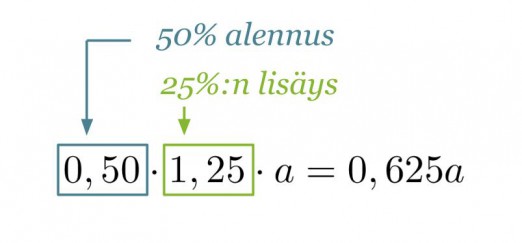
Klikkaa kuva suuremmaksi!
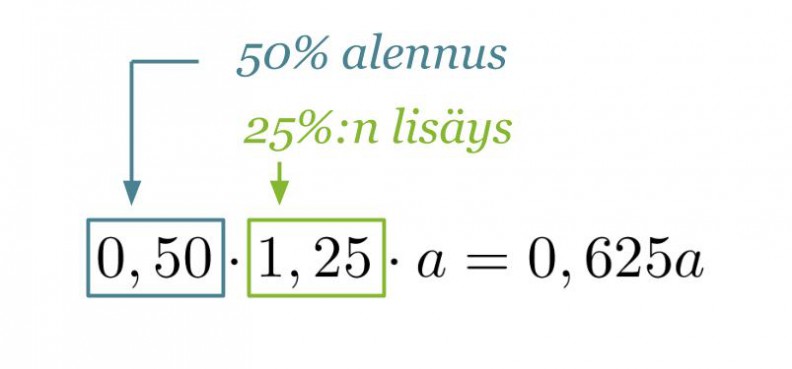
Klikkaa kuva suuremmaksi!
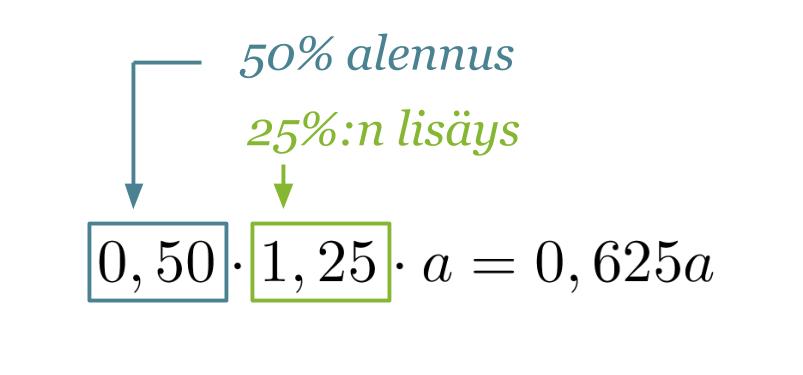
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Lasketaan lopuksi, montako prosenttia tämä on alkuperäisestä luvusta

Klikkaa kuva suuremmaksi!
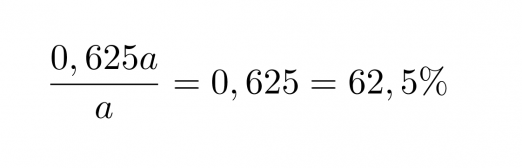
Klikkaa kuva suuremmaksi!
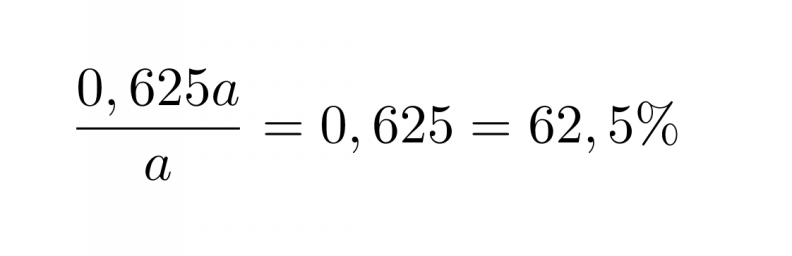
Klikkaa kuva suuremmaksi!
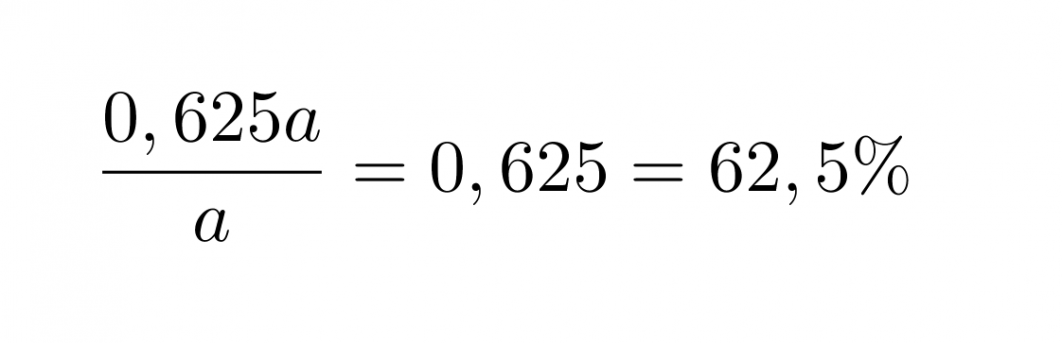
Klikkaa kuva suuremmaksi!
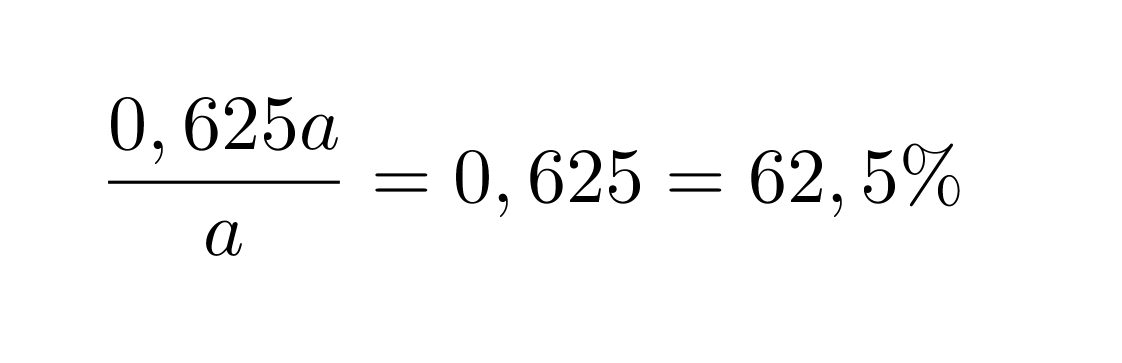
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Luku on 62,5 % alkuperäisestä luvusta.
Avoin matematiikka 8Osio 1: Yhtälöitä ja prosentteja4.6.2014