2. Kahden suoran leikkauspisteen määrittäminen
Jos tason suorat eivät ole keskenään yhdensuuntaisia, niin ne leikkaavat väistämättä toisensa jossakin pisteessä. Suorien leikkauspisteen koordinaatit saadaan selville, kun piirretään suorat samaan koordinaatistoon.
Esimerkki 1.
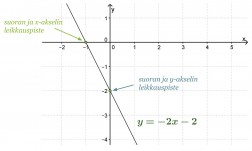
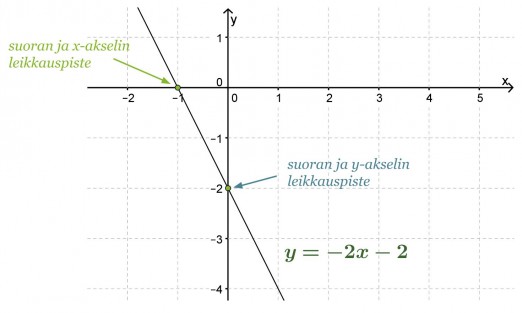
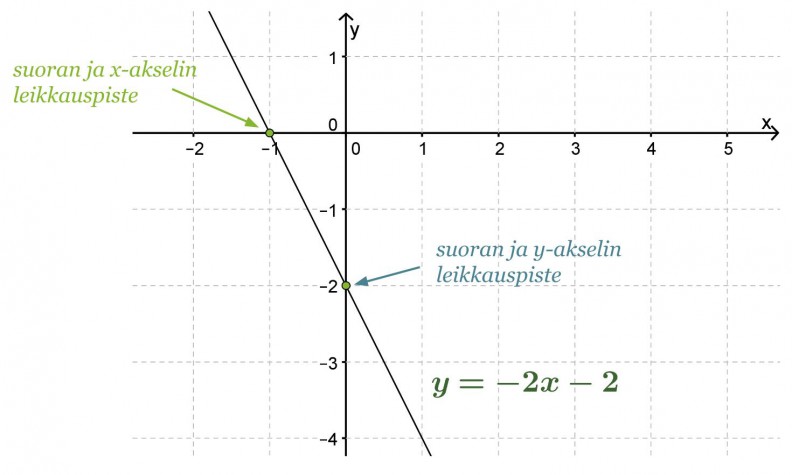
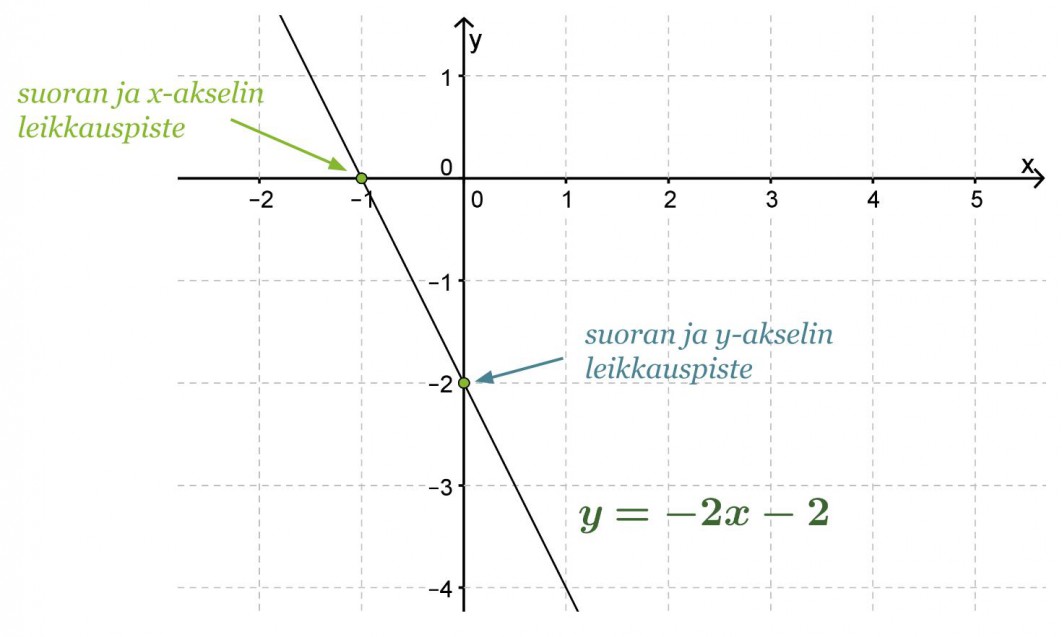
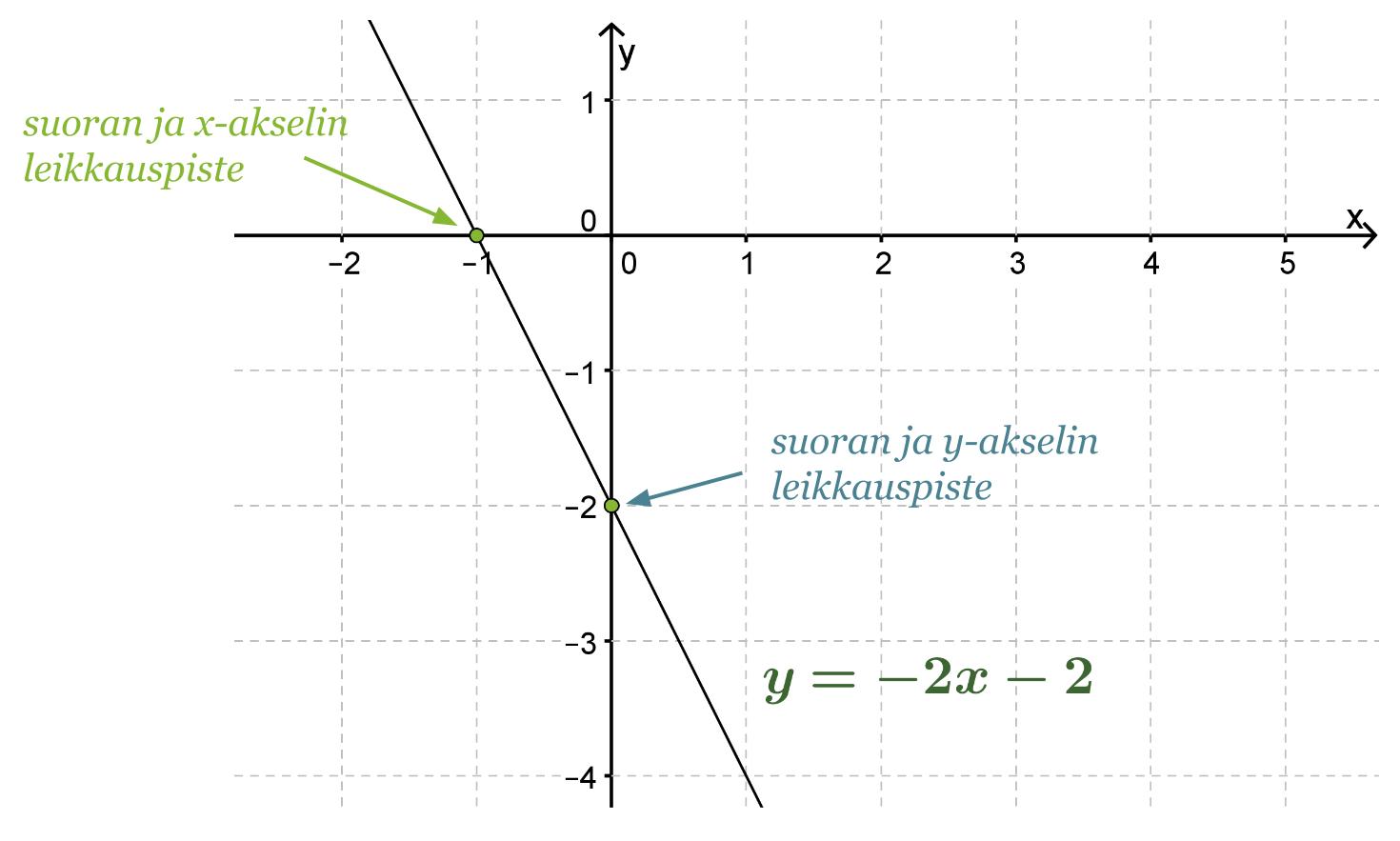
Määritetään piirtämällä suoran y= −2x − 2 ja koordinaattiakselien leikkauspisteet.
Lasketaan y:n arvoja muutamilla x:n arvoilla, sijoitetaan saadut pisteet koordinaatistoon ja piirretään niiden kautta suora.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Suora leikkaa x-akselin pisteessä (-1, 0) ja y-akselin pisteessä (0, -2).
Huom! Yhtälön −2x − 2 = 0 ratkaisu x = -1 löytyy suoran y= −2x − 2 ja x-akselin leikkauspisteestä.
Esimerkki 2.
Ratkaistaan yhtälö 4x – 7 = 2x – 1 piirtämällä.
Sievennetään ensin lauseke 4x – 7 = 2x – 1 tuomalla kaikki termit yhtälön vasemmalle puolelle.
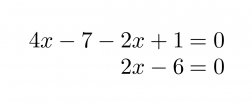
Klikkaa kuva suuremmaksi!
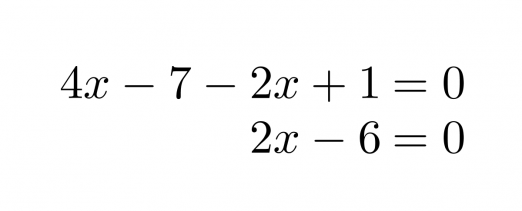
Klikkaa kuva suuremmaksi!
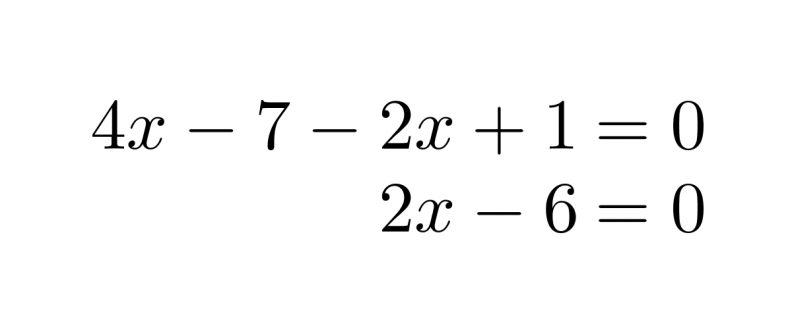
Klikkaa kuva suuremmaksi!
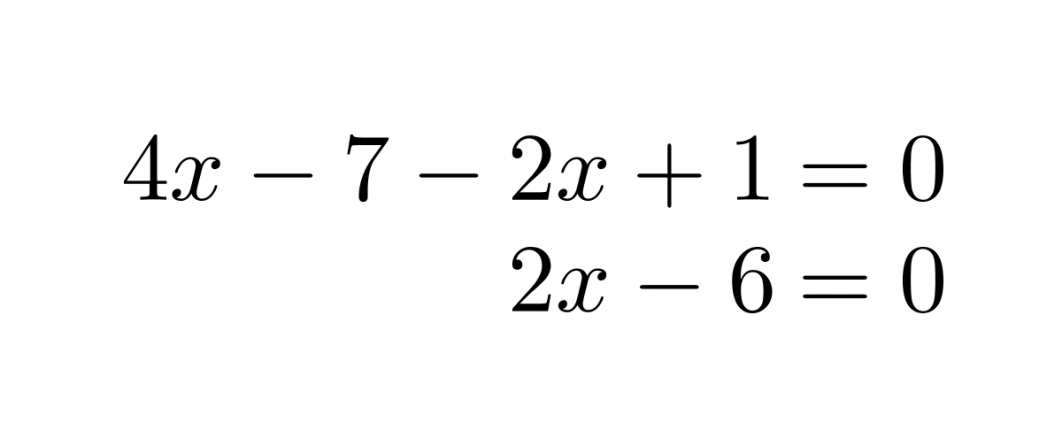
Klikkaa kuva suuremmaksi!
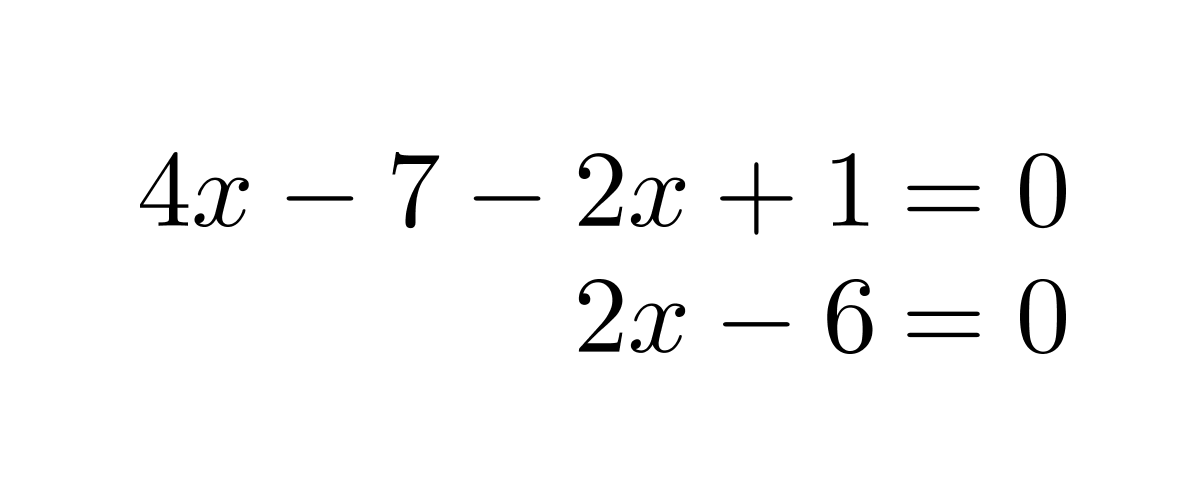
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
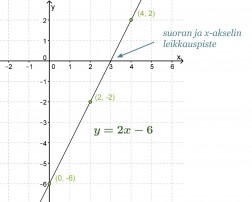
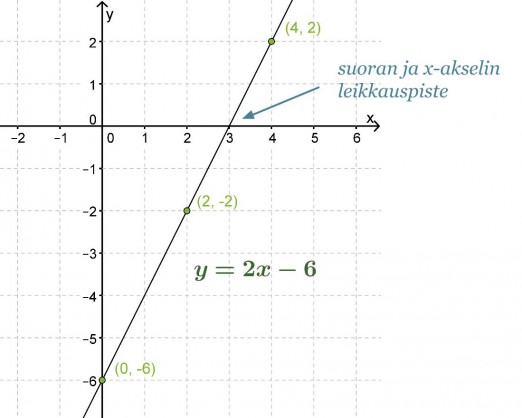
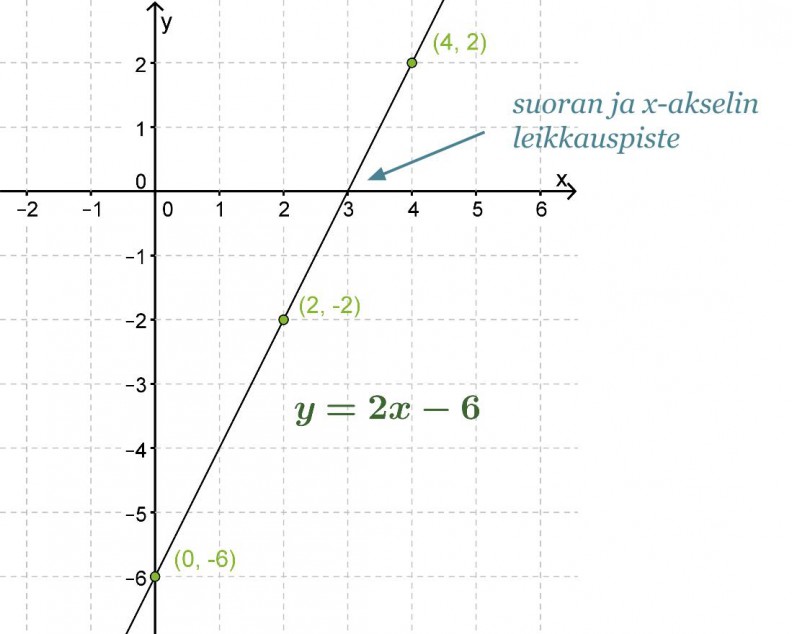
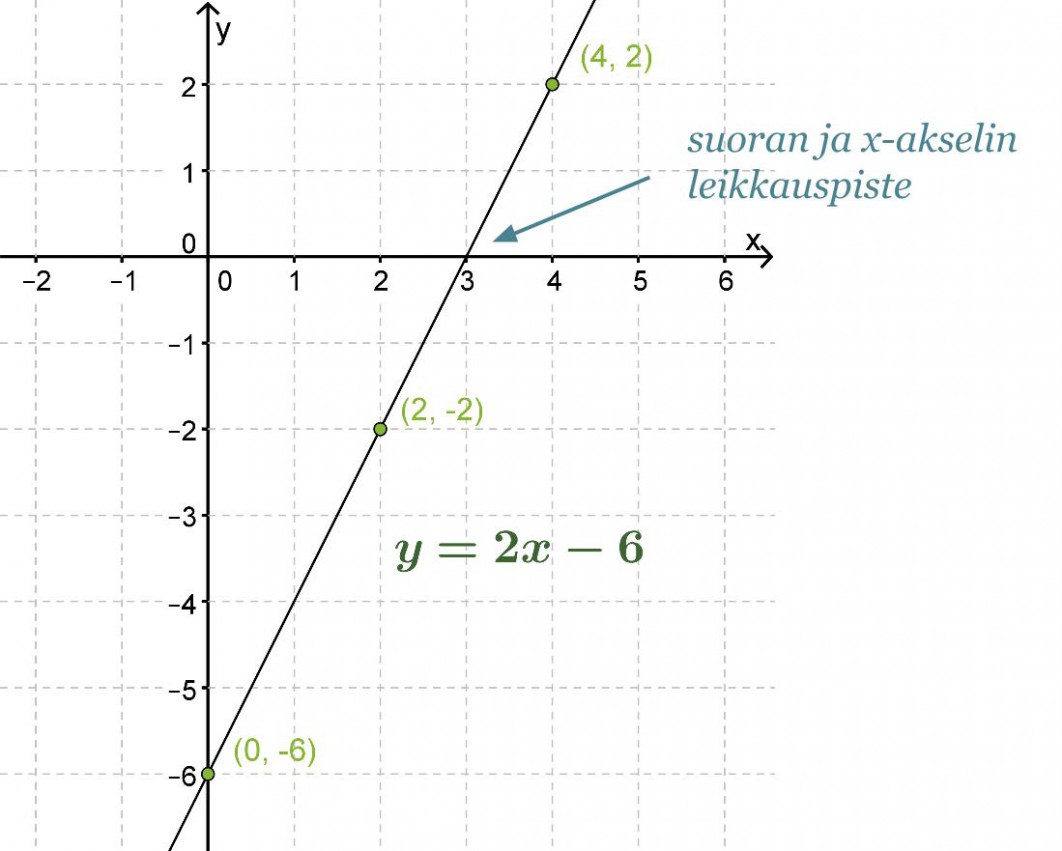
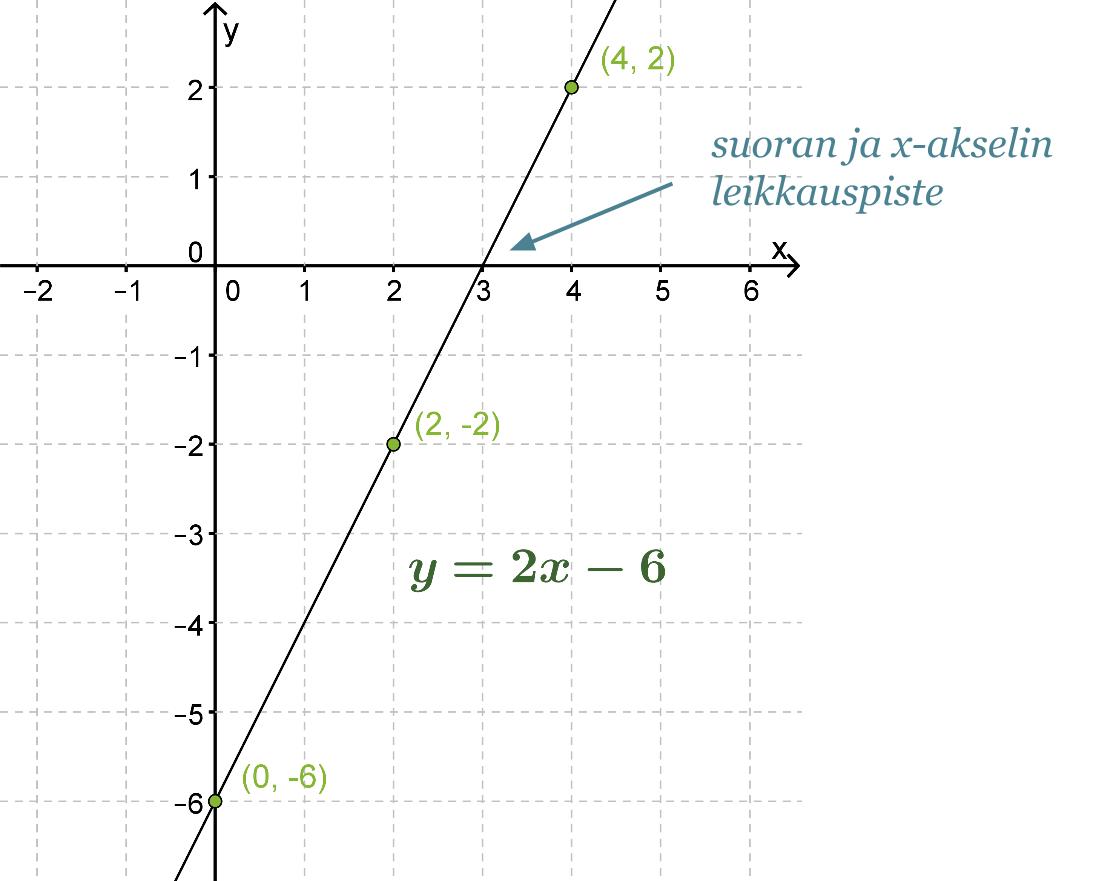
Piirretään suora y = 2x − 6 koordinaatistoon.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Yhtälön ratkaisu löytyy suoran ja x-akselin leikkauspisteestä eli x = 3.
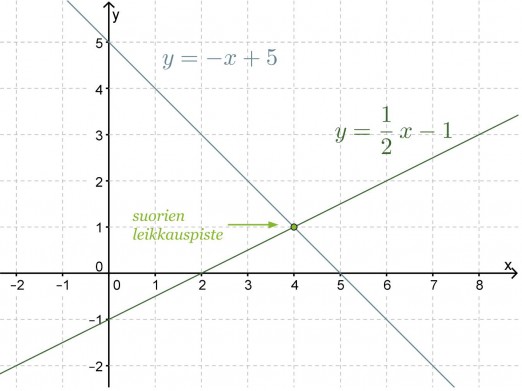
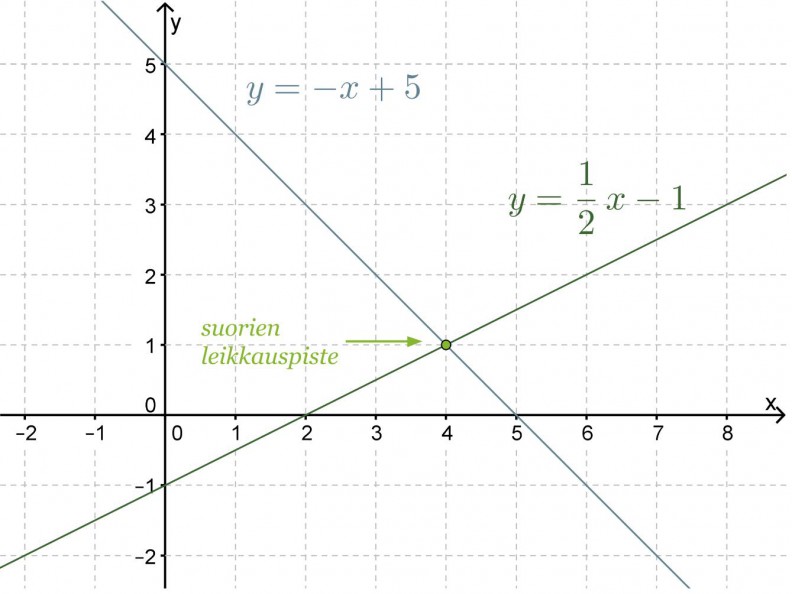
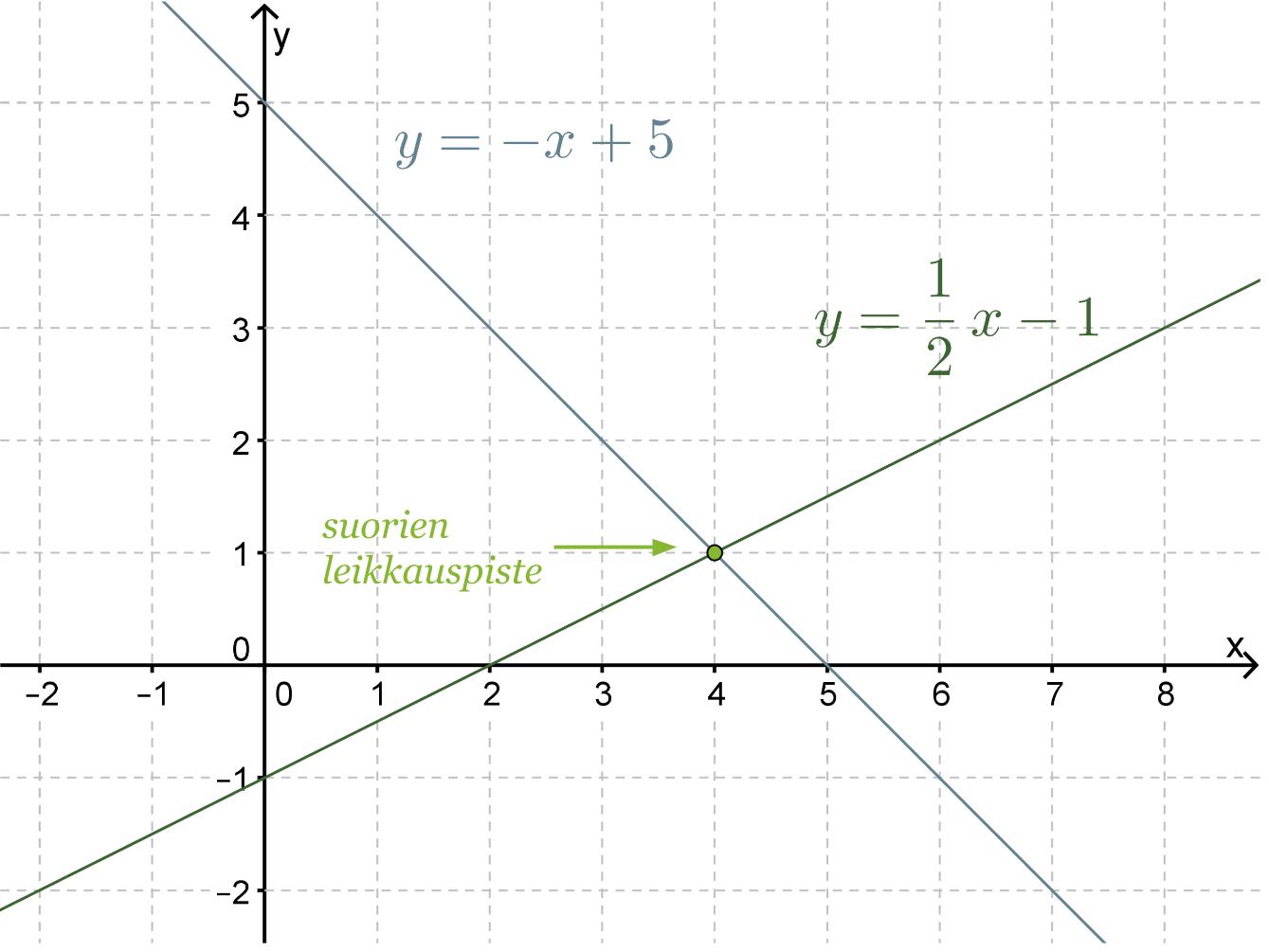
Esimerkki 3.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
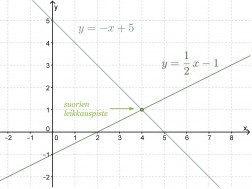
Piirretään ensin suorat samaan koordinaatistoon.

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!

Klikkaa taulukko suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Suorien leikkauspisteen koordinaatit ovat (4, 1).
Avoin matematiikka 8Osio 2: Suoria ja verrannollisuuksia4.6.2014