4. Muotoa y = kx + b oleva suoran yhtälö
Suoran piirtämiseksi koordinaatistoon ei tarvitse välttämättä taulukoida ensiksi pisteitä, jos osaa tulkita suoran kulun sen yhtälöstä. Tätä varten suoran yhtälö ratkaistaan y:n suhteen. Tuttuja yhtälön ratkaisutapoja käyttäen siirretään muut termit, paitsi muuttuja y, yhtälön oikealle puolelle.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
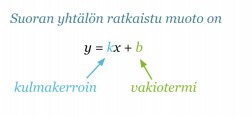
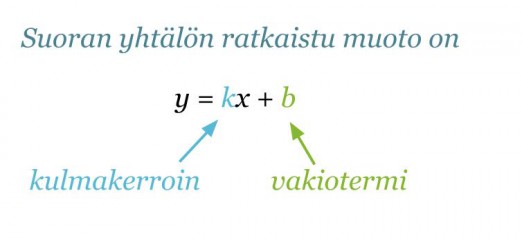
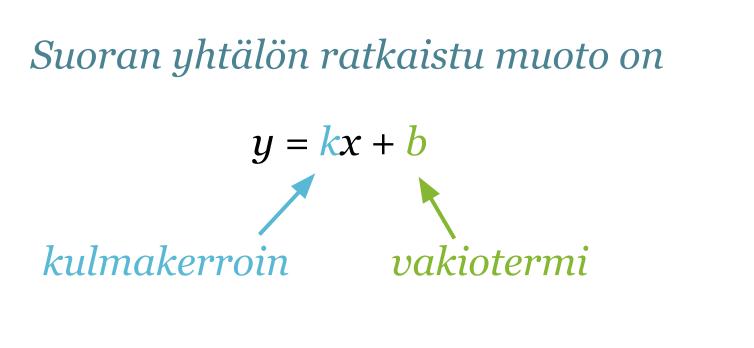
Suoran yhtälön ratkaistu muoto on y = kx + b.
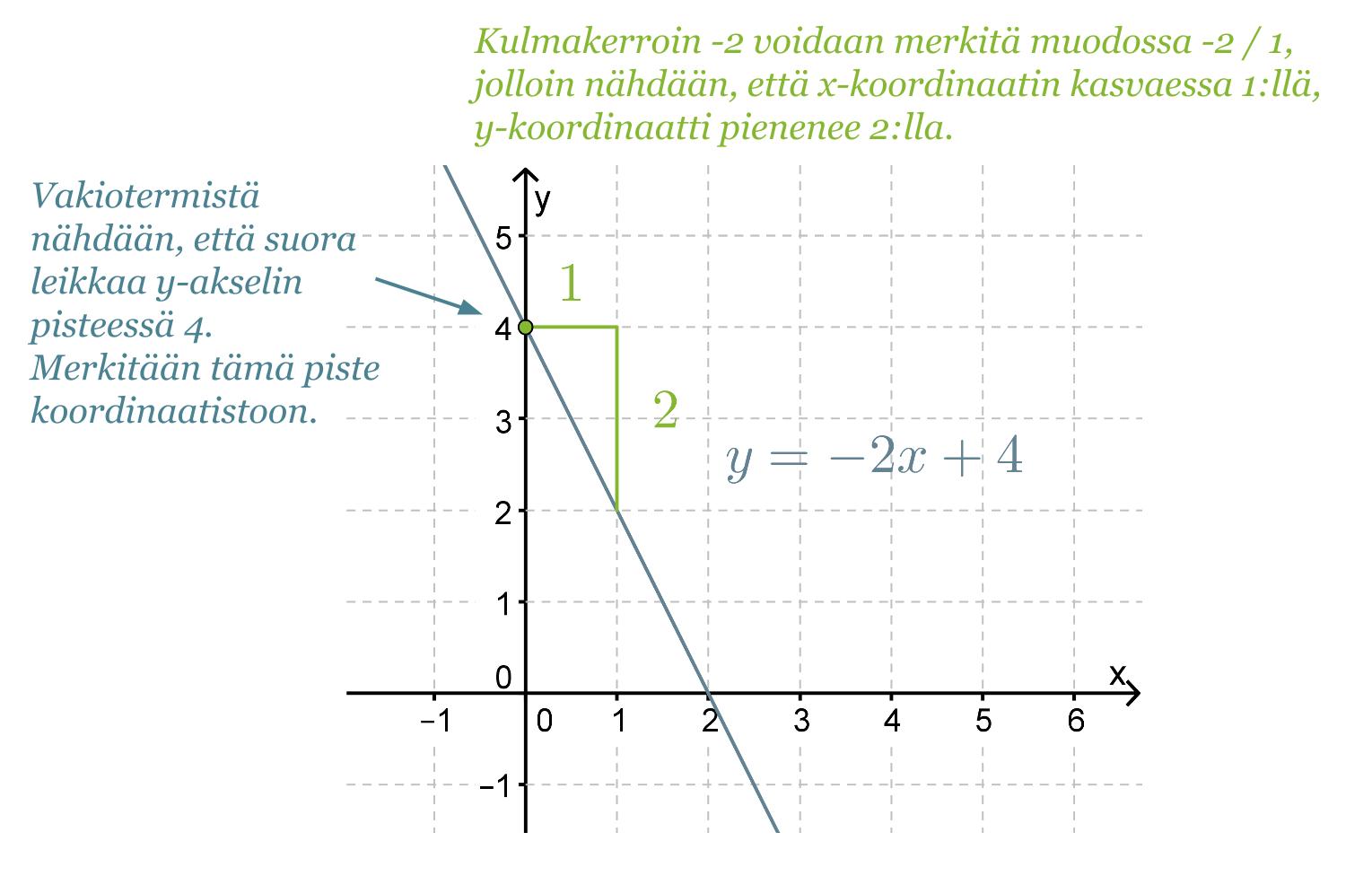
Vakiotermi b kertoo kohdan, jossa suora leikkaa y-akselin. Yhtälön kulmakertoimesta nähdään, onko suora nouseva vai laskeva.
Esimerkki 1.
Mikä on suoran kulmakerroin ja mikä vakiotermi? Onko suora nouseva vai laskeva?
a) y = 2x + 1
b) y = x – 6
c) y = -4x +3
Ratkaisu:
a) Kulmakerroin on 2 ja vakiotermi on 1. Koska kulmakerroin on positiivinen, on suora nouseva.
b) Kulmakerroin on 1 ja vakiotermi on -6. Koska kulmakerroin on positiivinen, on suora nouseva.
c) Kulmakerroin on -4 ja vakiotermi 3. Koska kulmakerroin on negatiivinen, on suora laskeva.
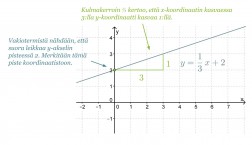
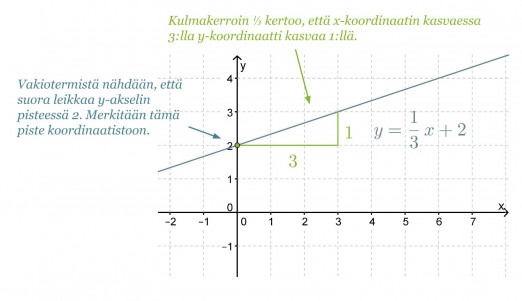
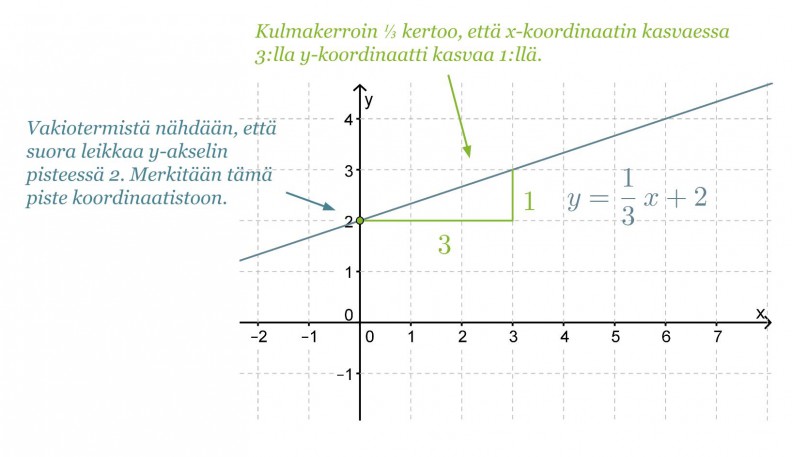
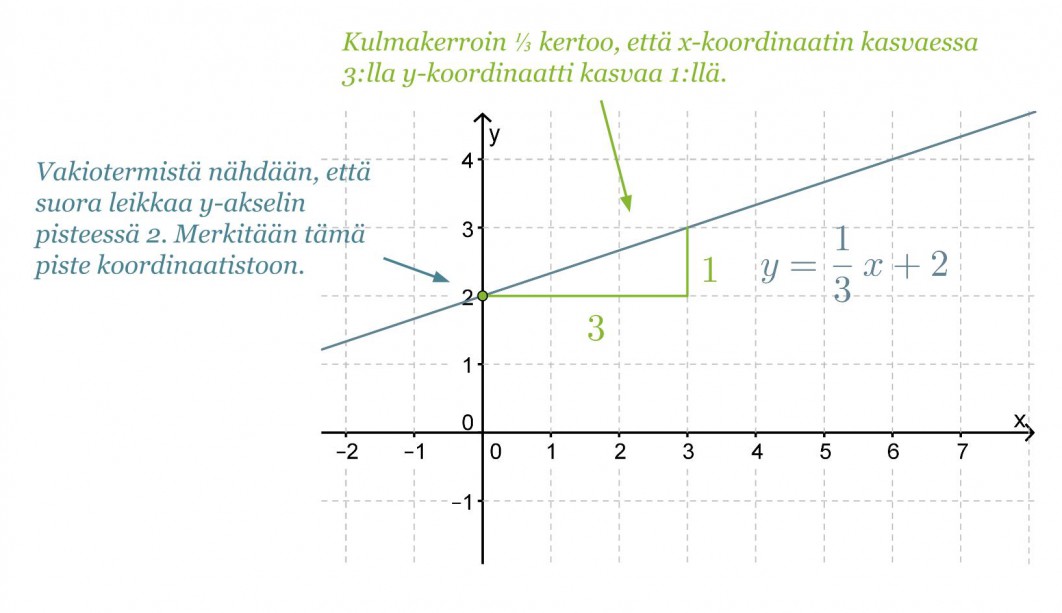
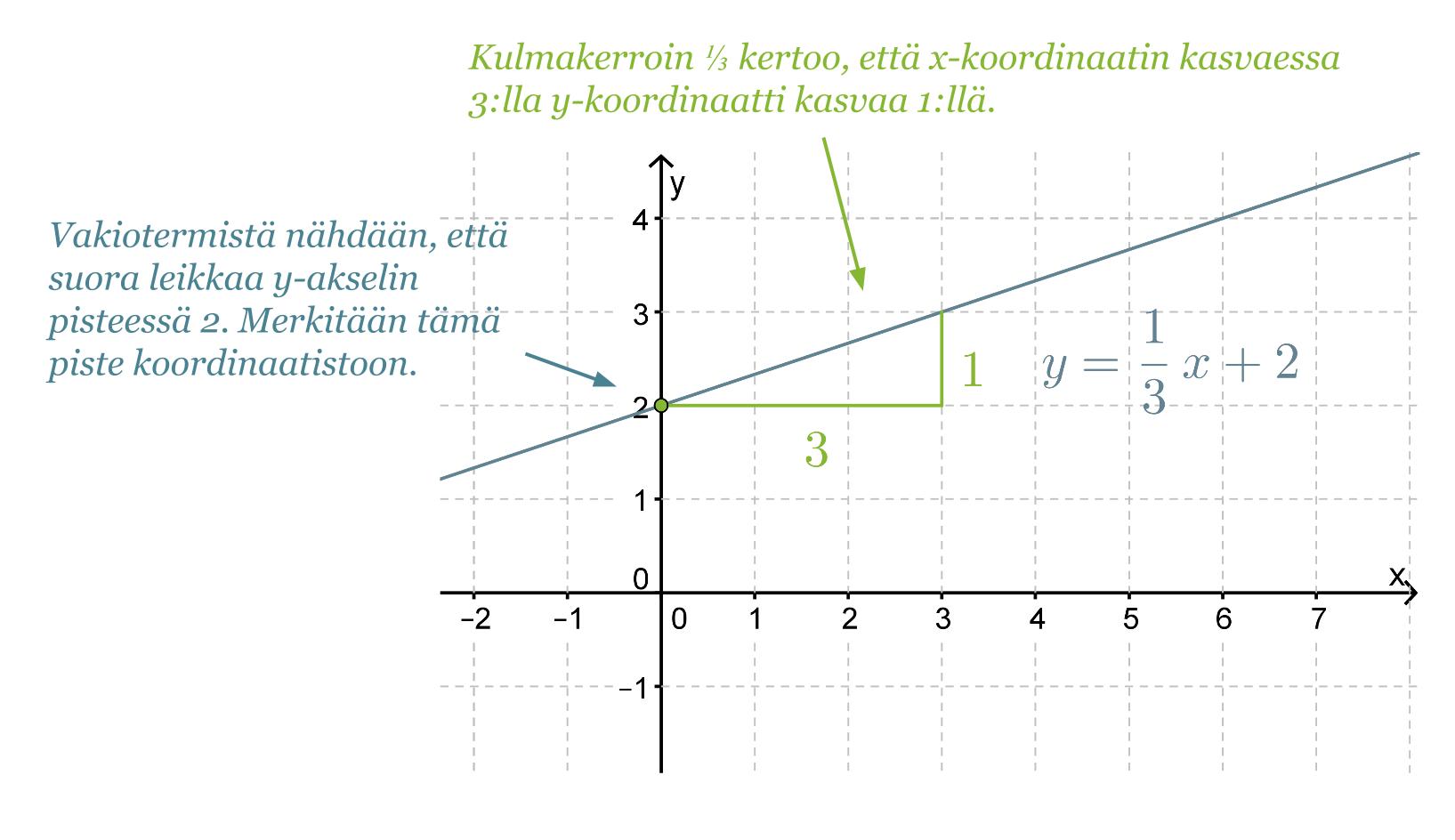
Suoran piirtämiseksi koordinaatistoon tarvitaan vähintään kaksi suoralla olevaa pistettä. Vakiotermi kertoo suoran kuvaajan ja y-akselin leikkauspisteen y-koordinaatin. Toinen pisteistä määritetään kulmakertoimesta. Siirrytään koordinaatistossa y-akselin leikkauspisteestä kulmakertoimen nimittäjän ilmoittama määrä x-akselin suuntaisesti ja osoittajan ilmoittama määrä y-akselin suuntaisesti.
Huom! Origon kautta kulkevan suoran yhtälöstä puuttuu vakiotermi kokonaan, joten se on muotoa y = kx.
Esimerkki 2.
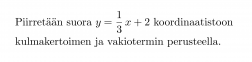
Klikkaa kuva suuremmaksi!
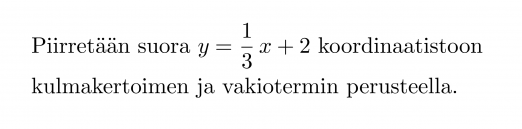
Klikkaa kuva suuremmaksi!
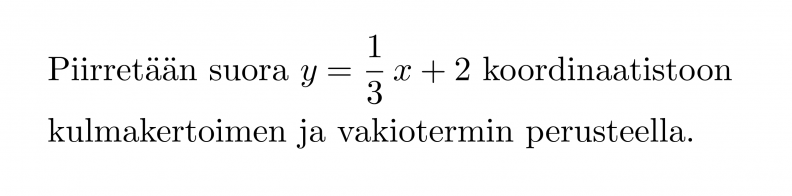
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
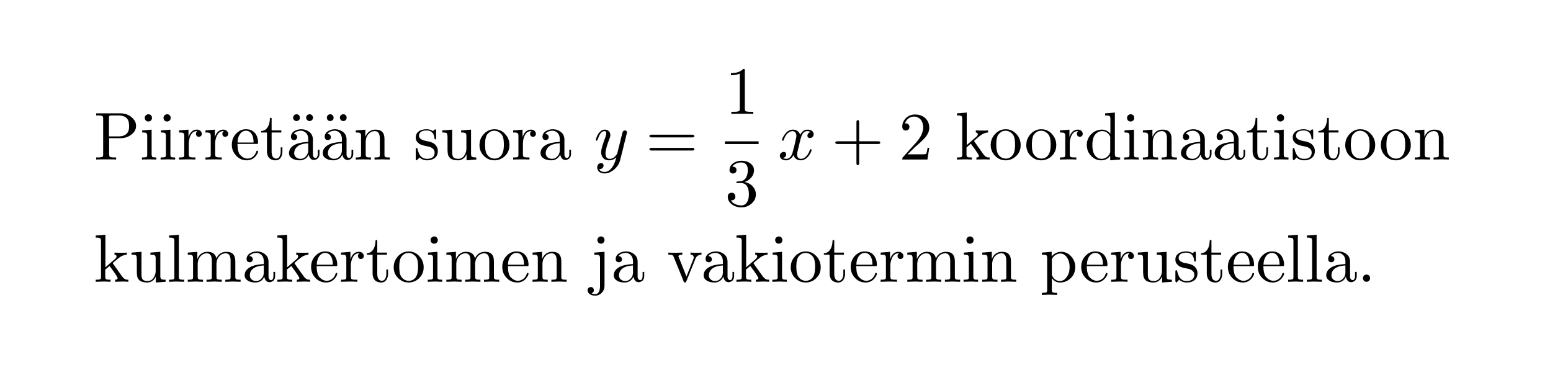
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
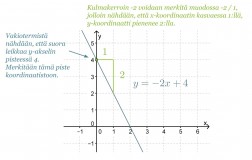
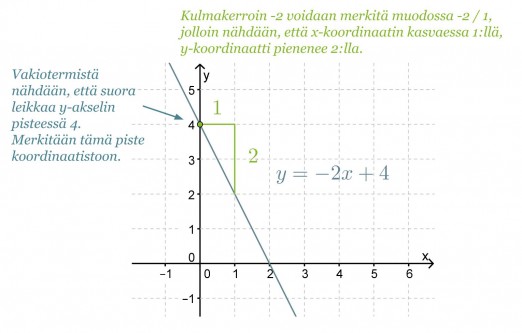
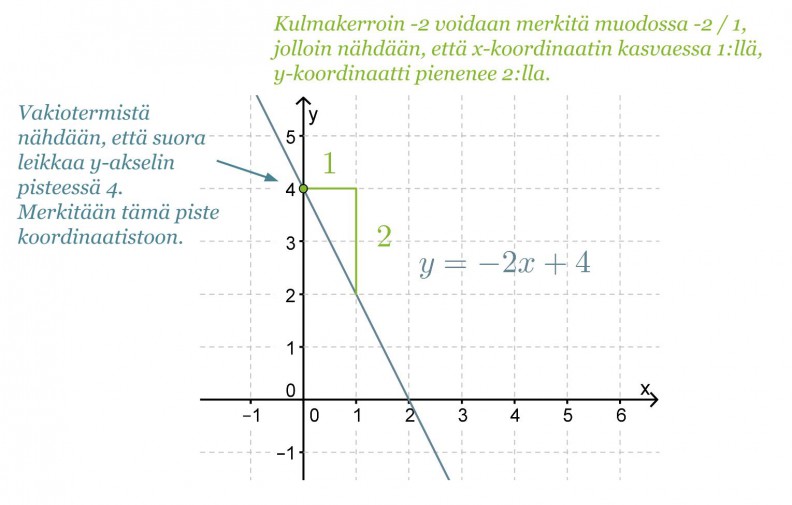
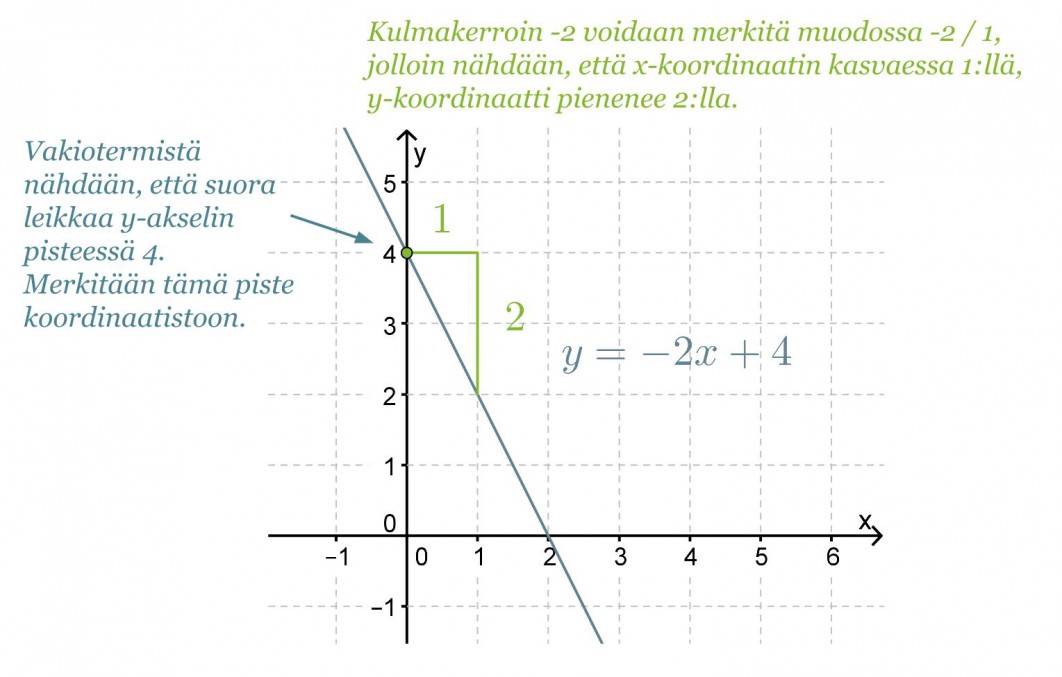
Esimerkki 3.
Piirretään suora y = -2x + 4 koordinaatistoon kulmakertoimen ja vakiotermin perusteella.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!