6. Suoran yhtälön muodostaminen
Suoran yhtälö voidaan muodostaa suoran kuvaajan perusteella. Jos tunnetaan kaksi suoran pistettä, saadaan yhtälö määritettyä ilman kuvaajaa.
Esimerkki 1.
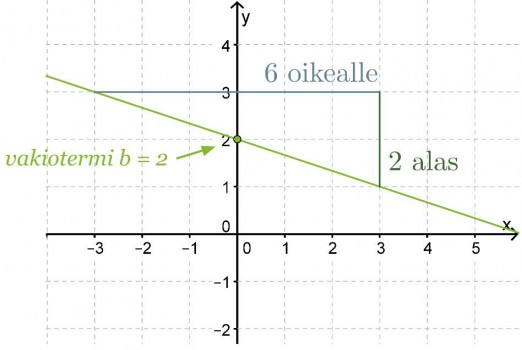
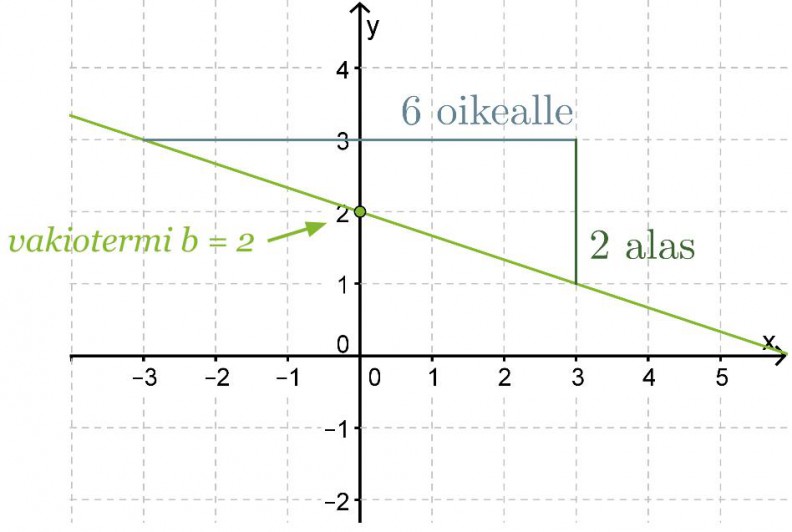
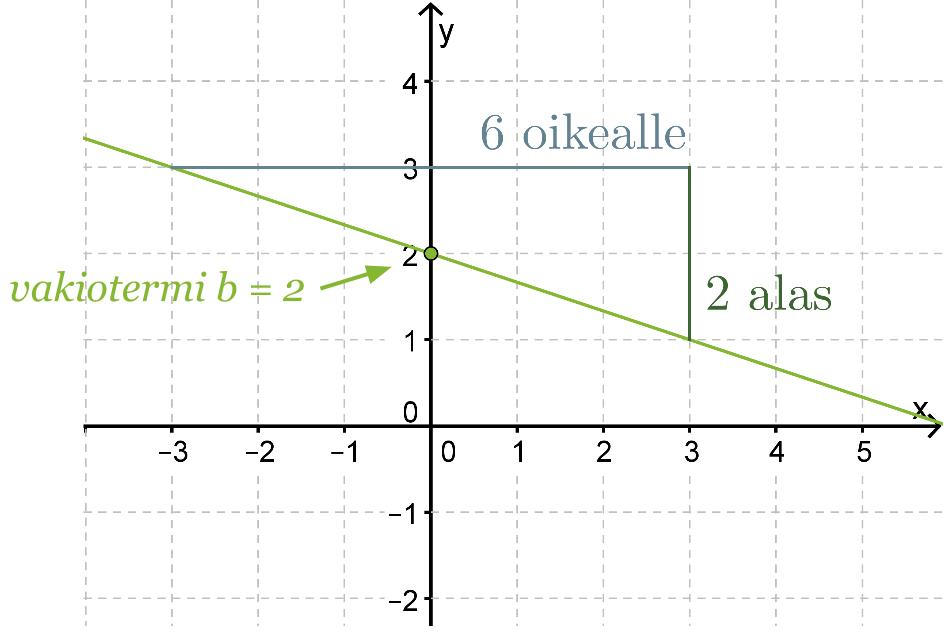
Määritetään kuvassa olevan suoran yhtälö.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suoran yhtälö on muotoa y = kx + b. Vakiotermi b saadaan suoran ja y-akselin leikkauspisteestä eli tässä tapauksessa b = 2. Kulmakerroin k on
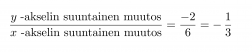
Klikkaa kuva suuremmaksi!
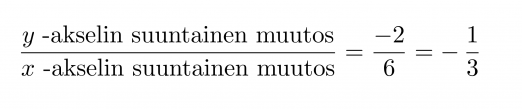
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
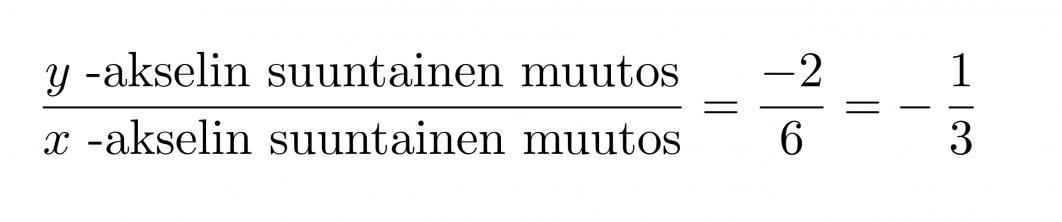
Klikkaa kuva suuremmaksi!
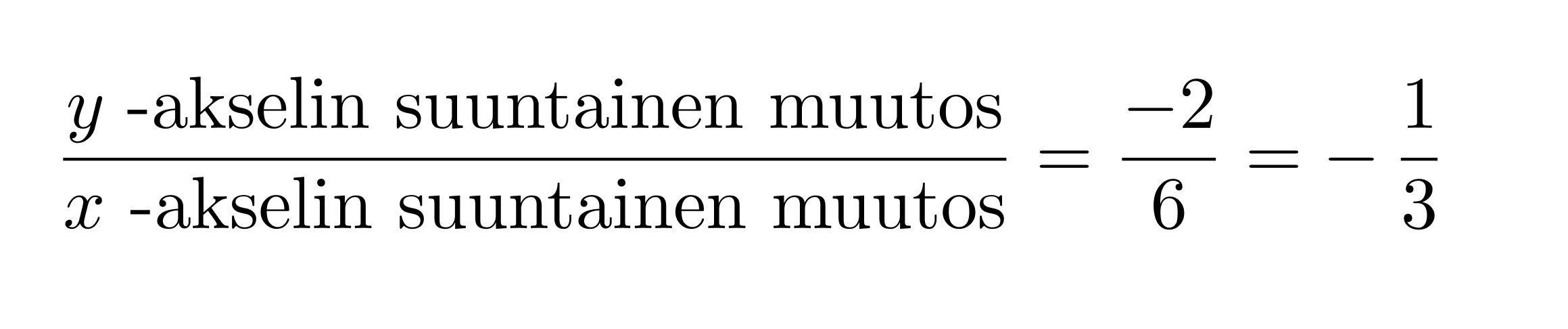
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Suoran yhtälö on
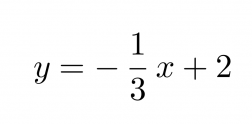
Klikkaa kuva suuremmaksi!
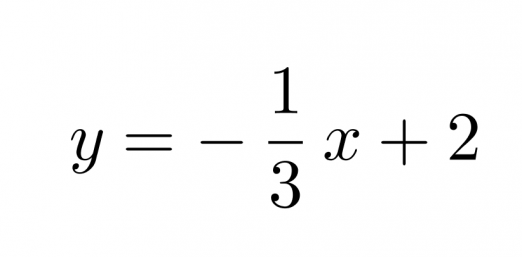
Klikkaa kuva suuremmaksi!
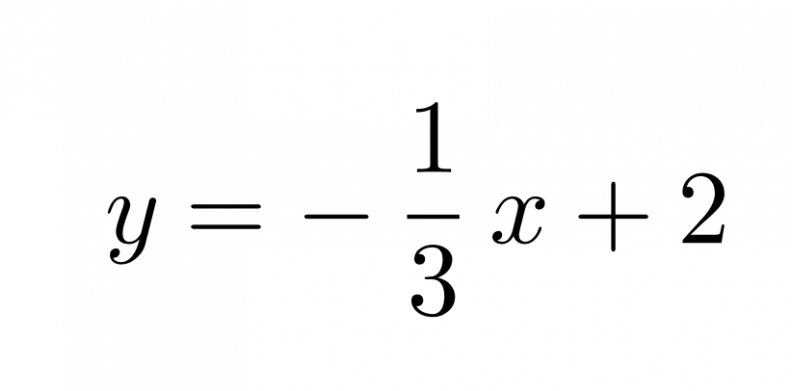
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Suora kulkee pisteiden (-1, -6) ja (2, 0) kautta. Määritetään suoran yhtälö piirtämättä suoran kuvaajaa.
Lasketaan annettujen pisteiden avulla suoran kulmakerroin:
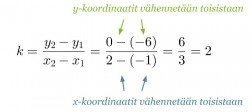
Klikkaa kuva suuremmaksi!
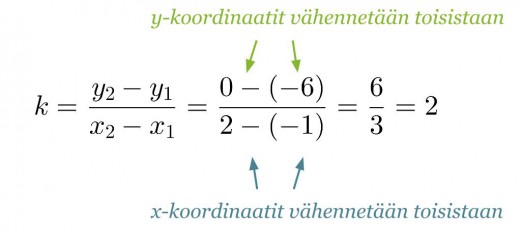
Klikkaa kuva suuremmaksi!
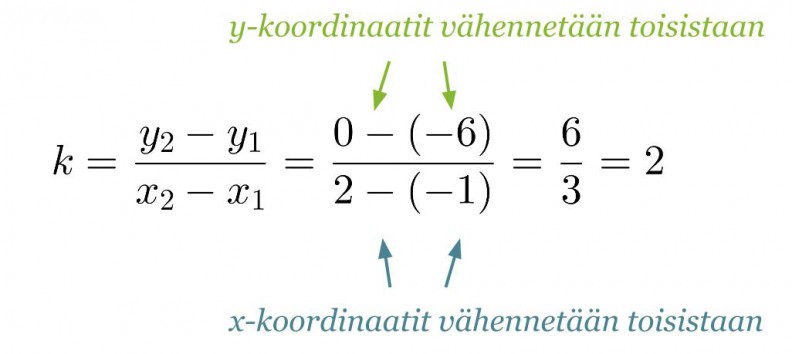
Klikkaa kuva suuremmaksi!
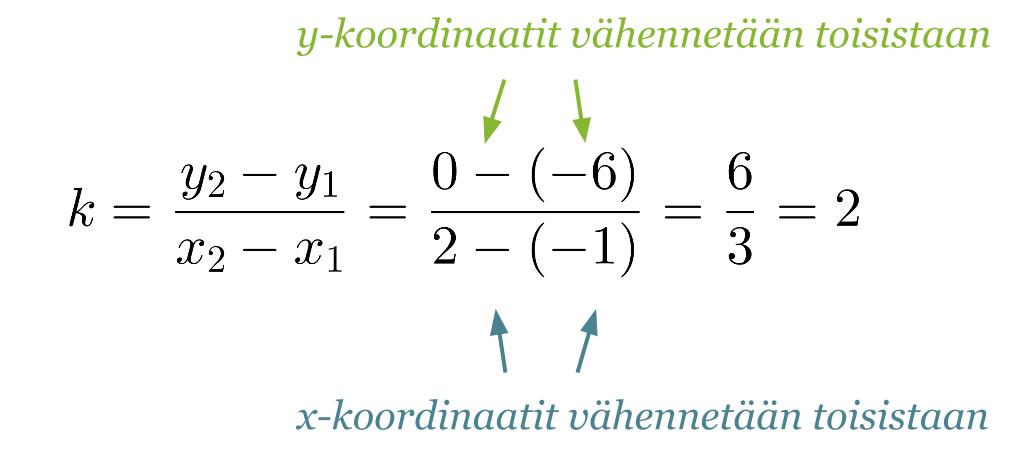
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suoran yhtälö on siis muotoa y = 2x + b. Vakiotermin b ratkaisemiseksi sijoitetaan jompi kumpi suoran pisteistä suoran lausekkeeseen ja ratkaistaan saatu yhtälö muuttujan b suhteen. Valitan tarkastelupisteeksi (-1, -6).
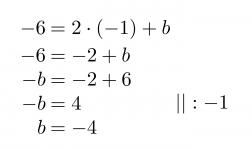
Klikkaa kuva suuremmaksi!
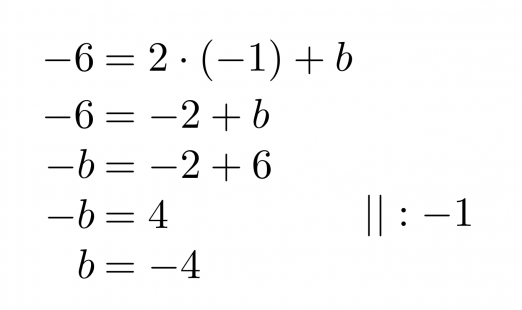
Klikkaa kuva suuremmaksi!
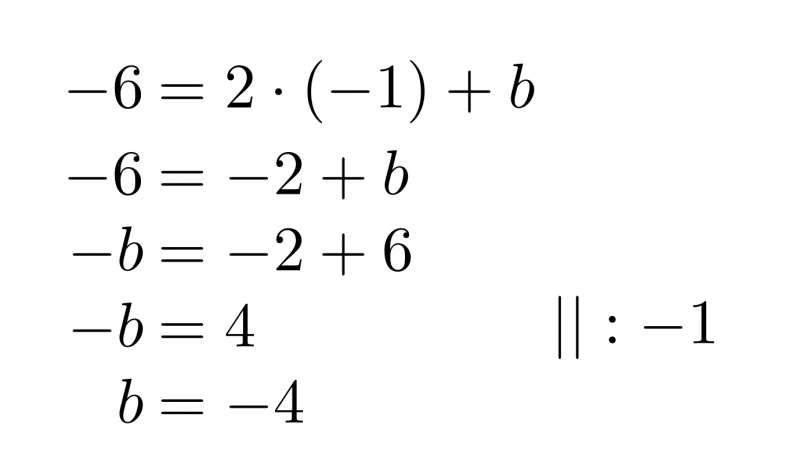
Klikkaa kuva suuremmaksi!
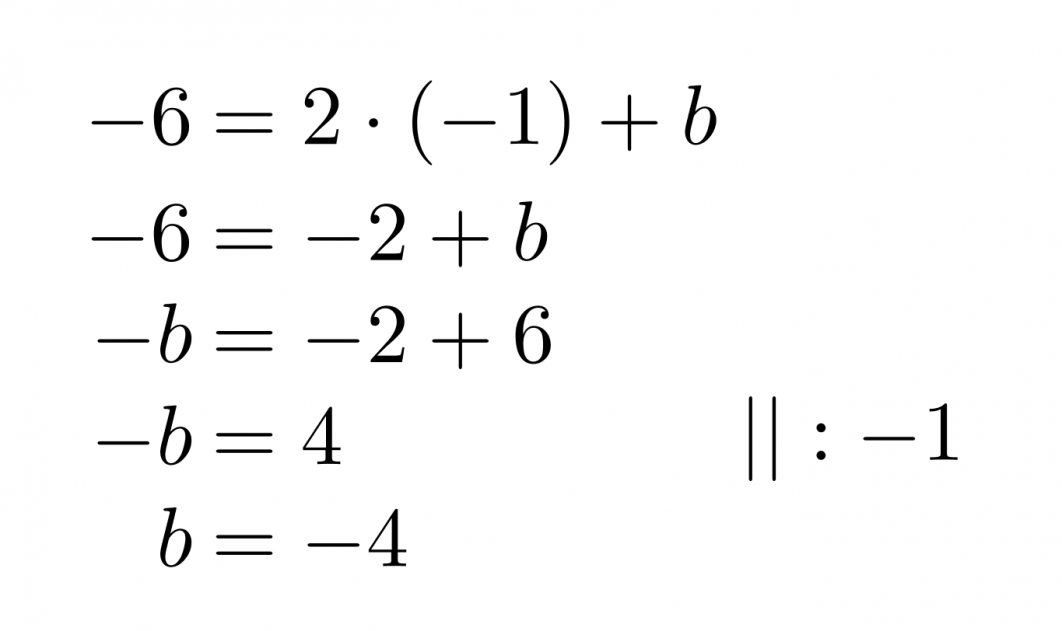
Klikkaa kuva suuremmaksi!
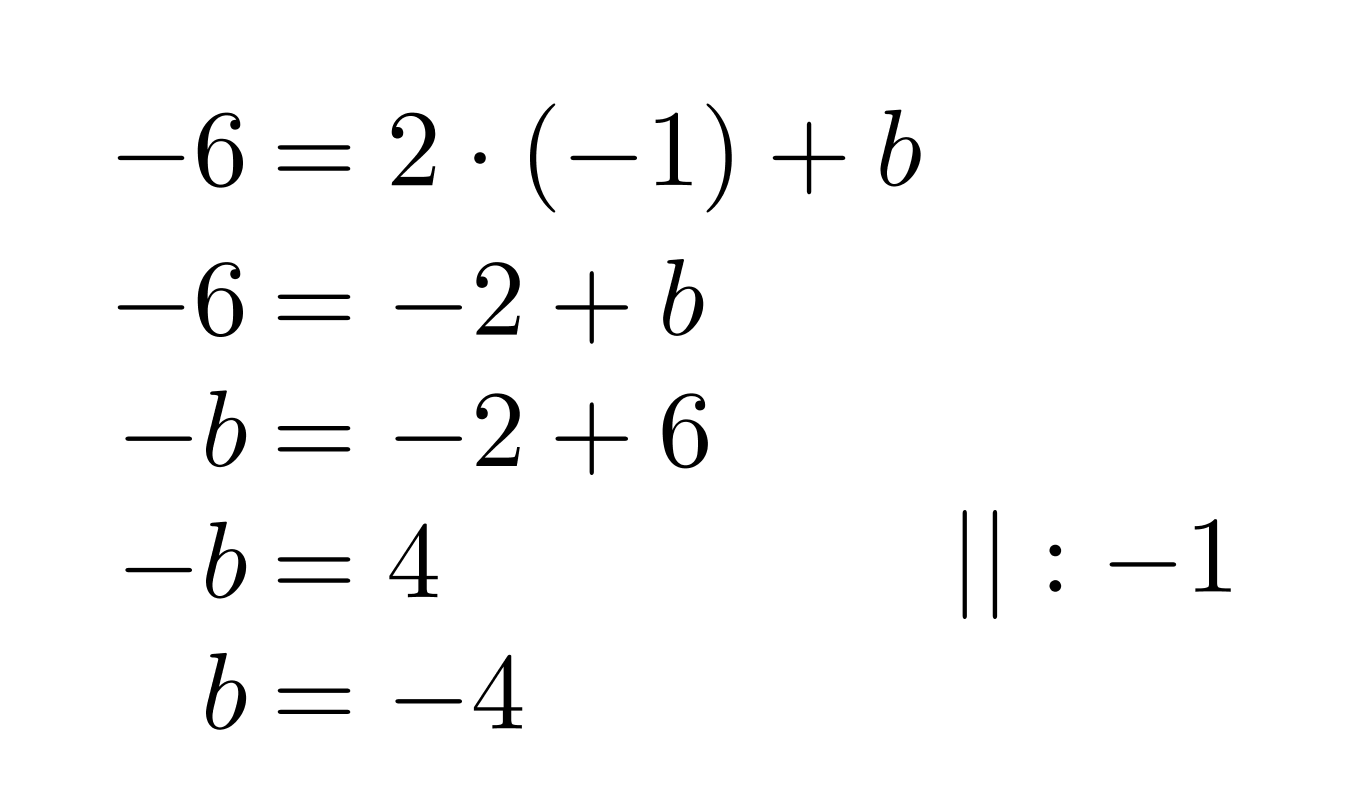
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Suoran yhtälö on y = 2x – 4.
Huom! Suoran yhtälö yleisessä muodossa on 2x – y – 4 = 0.
Avoin matematiikka 8Osio 2: Suoria ja verrannollisuuksia4.6.2014