12. Suoraan verrannollisuus
Verrantoa käytetään usein hyödyksi ongelmien ratkaisemisessa. Ennen kuin voidaan muodostaa kahden suhteen verranto, on pääteltävä, onko kysymyksessä suoraan vai kääntäen verrannollisuus.
Tuntipalkalla työtä tekevä henkilö tietää ansaitsevansa sitä enemmän, mitä useamman tunnin hän työskentelee. Palkka ja tehtyjen tuntien määrä kasvavat siis samassa suhteessa. Suoraan verrannollisuus tulee esille myös esimerkiksi ostoksilla. Mitä enemmän jotakin tavaraa ostetaan, sitä enemmän ostokset maksavat.
Suureita, joiden suhde on vakio, sanotaan suoraan verrannollisiksi. Jos toinen suure kasvaa kaksinkertaiseksi, kasvaa toinenkin kasinkertaiseksi. Jos toinen suure puolestaan pienenee neljäsosaan, myös toinen pienenee neljäsosaan.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kun suoraan verrannollisten suureiden riippuvuutta kuvataan koordinaatistossa, pisteet osuvat samalle origon kautta kulkevalle suoralle. Suoraan verrannolliset suureet riippuvat lineaarisesti toisistaan.
Esimerkki 1.
Laura teki töitä 15 tuntia ja sai palkkaa 90 €. Jenna työskenteli puolestaan 18 tuntia palkalla 108 €. Ovatko työaika ja palkka suoraan verrannollisia?
Ratkaisu:
Työaika ja palkka ovat suoraan verrannollisia, jos tuntipalkka pysyy muuttumattomana.
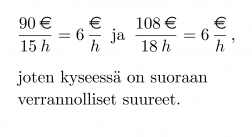
Klikkaa kuva suuremmaksi!
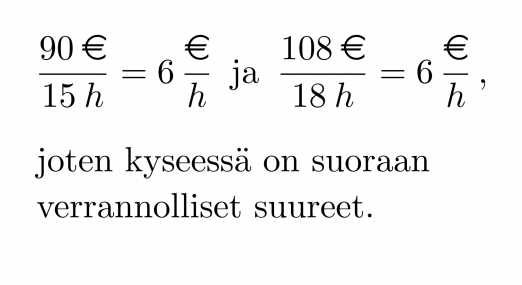
Klikkaa kuva suuremmaksi!
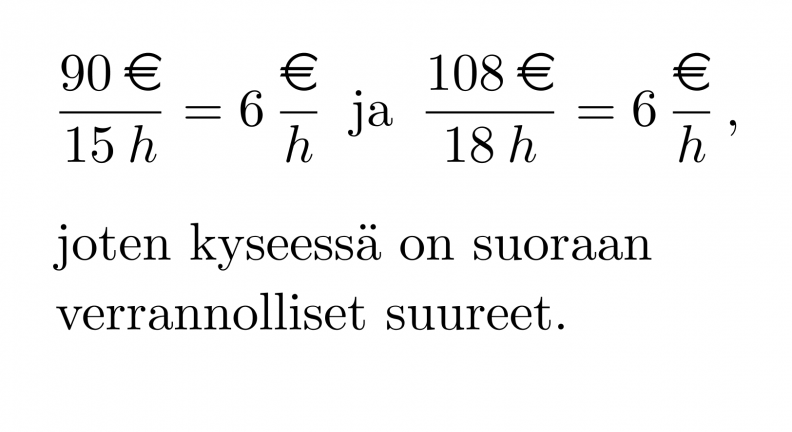
Klikkaa kuva suuremmaksi!
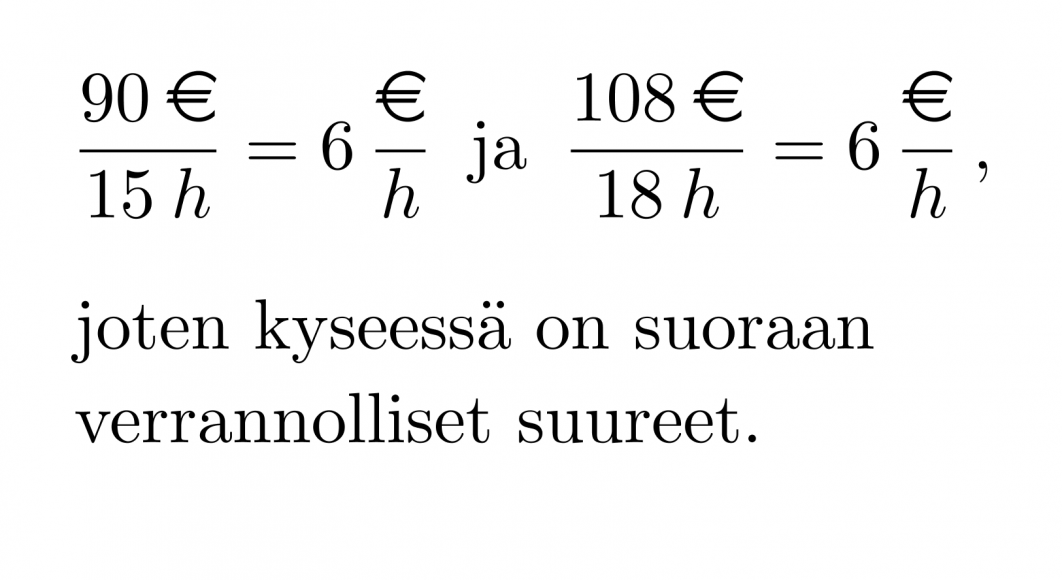
Klikkaa kuva suuremmaksi!
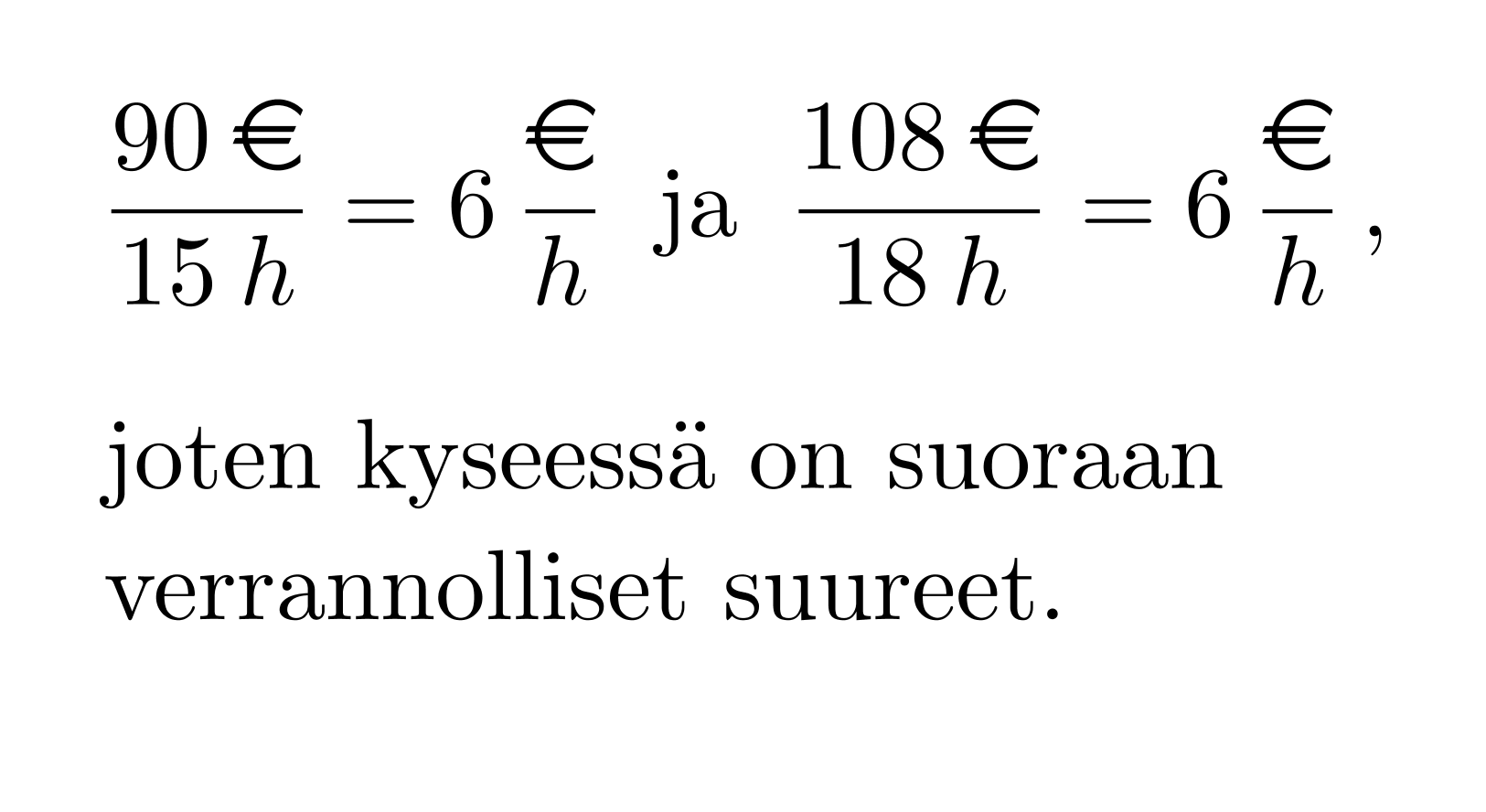
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Kolme kiloa mangoja maksaa 6,90 €. Paljonko maksaa viisi kiloa samoja mangoja?
Ratkaisu:
Verrannon muodostamisessa voidaan käyttää hyväksi asetelmaa. Merkitään kysyttyä hintaa x:llä ja laaditaan asetelma mangojen massalle ja hinnalle.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Hinnan kasvusuunta on pääteltävä. Loogisesti suurempi määrä samaa tuotetta maksaa enemmän. Koska nuolet ovat samansuuntaisia, on kyseessä suoraan verrannolliset suureet. Verranto voidaan muodostaa suoraan asetelmasta:

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Voidaan valita, laitetaanko jakoviivojen yläpuolelle pienemmät vai suuremmat arvot, kunhan toimitaan samalla tavoin yhtälön molemmilla puolilla (eli nuolien suunta on säilyttävä samana molemmilla puolilla yhtälöä).
Ristiin kertomalla edellinen yhtälö saadaan muotoon:

Klikkaa kuva suuremmaksi!
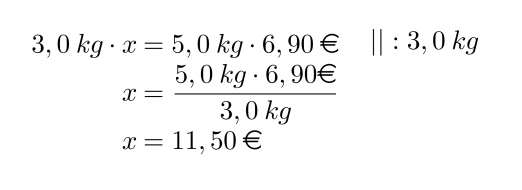
Klikkaa kuva suuremmaksi!
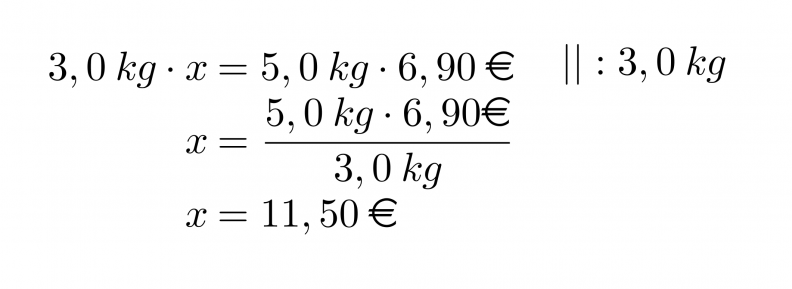
Klikkaa kuva suuremmaksi!
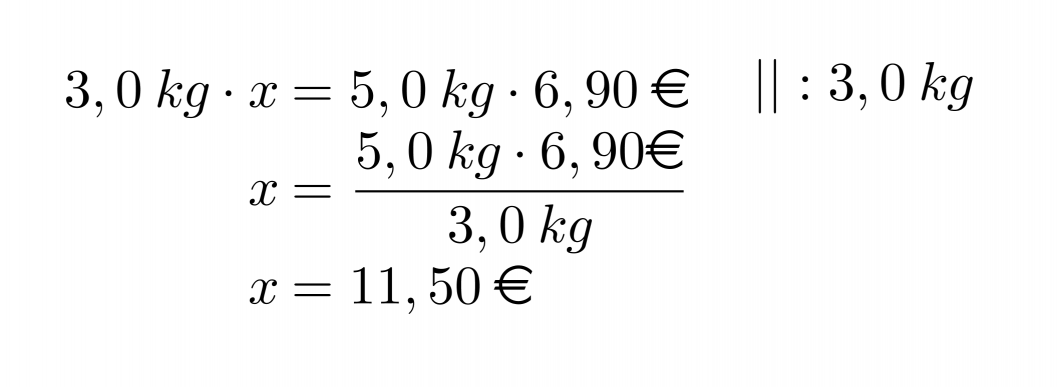
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: 5,0 kg mangoja maksaa 11,50 €.
Huom! Sijoitettaessa suureen arvoja verrantoon on tärkeää, että ne sijoitetaan laatuineen. Tällaisella suurelaskennalla on se etu, että tuloksen laadusta voidaan jo päätellä, onko tulos oikein.
Avoin matematiikka 8Osio 2: Suoria ja verrannollisuuksia4.6.2014