1. Yhtenevät ja yhdenmuotoiset kuviot

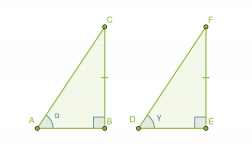
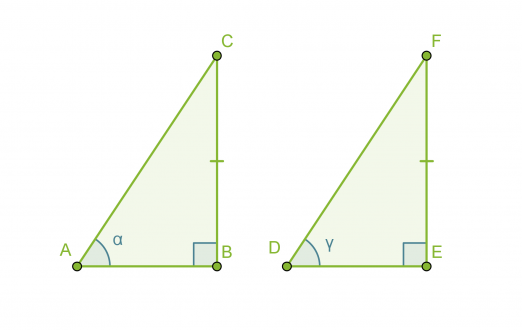
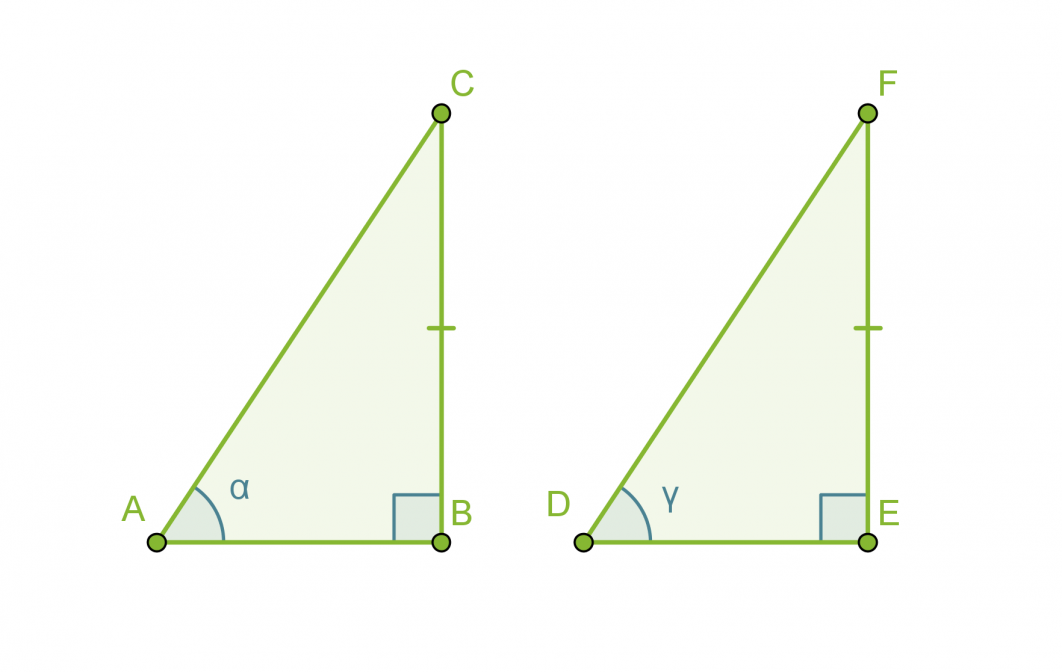
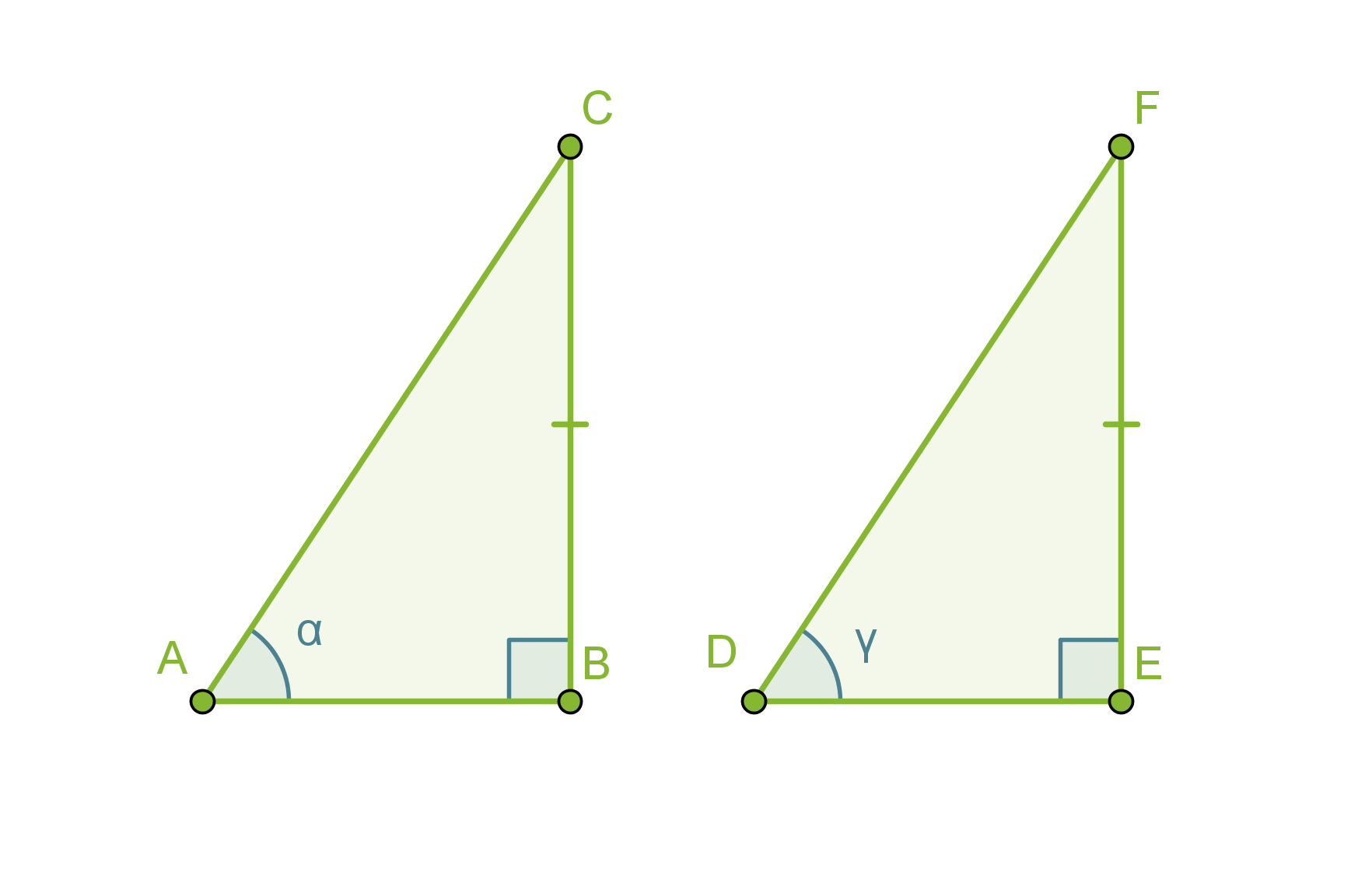
Kol­mi­ot ABC ja DEF ovat kes­ke­nään yh­te­ne­viä, mikä voi­daan mer­ki­tä seu­raa­vas­ti: ABC ≅ DEF. Sym­bo­li ~ tar­koit­taa sa­maa muo­toa ja = sa­maa ko­koa. Pääl­lek­käin ase­tet­tu­na yh­te­ne­vät ku­vi­ot siis peit­tä­vät täy­del­li­ses­ti toi­sen­sa.

Klik­kaa kuva suu­rem­mak­si!

Si­vut BC ja EF ovat tois­ten­sa vas­tin­si­vu­ja. Kul­mat α ja γ ovat puo­les­taan tois­ten­sa vas­tin­kul­mia. Ylei­ses­ti yh­den­muo­tois­ten ku­vi­oi­den vas­taa­via osia ni­mi­te­tään tois­ten­sa vas­tin­o­sik­si. Mitä mui­ta vas­tin­osia löy­dät?

Kes­ke­nään yh­den­muo­toi­sien ku­vi­oi­den voi­daan aja­tel­la syn­ty­vän si­ten, että ker­ro­taan tai ja­e­taan kaik­ki vas­tin­si­vut jol­la­kin sa­mal­la lu­vul­la. Vas­tin­kul­mat py­sy­vät yhtä suu­ri­na. Yh­den­muo­toi­suu­den merk­ki on ~.

Huom! Yh­te­ne­vät ku­vi­ot ovat aina myös yh­den­muo­toi­sia.

Yh­den­muo­toi­suu­den löy­ty­mi­nen hel­pot­taa mo­nien ge­o­met­ris­ten teh­tä­vien rat­kai­se­mis­ta. Yh­den­muo­tois­ten ku­vi­oi­den vas­tin­si­vu­jen pi­tuuk­sien suh­de säi­lyy sa­ma­na, jol­loin voi­daan muo­dos­taa ver­ran­to tun­te­mat­to­man si­vun pi­tuu­den rat­kai­se­mi­sek­si.

Esimerkki 1.

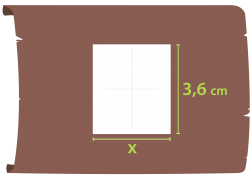
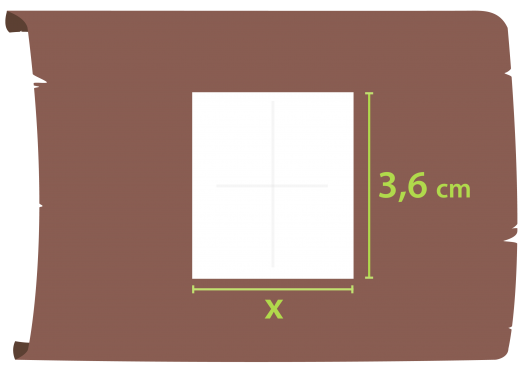
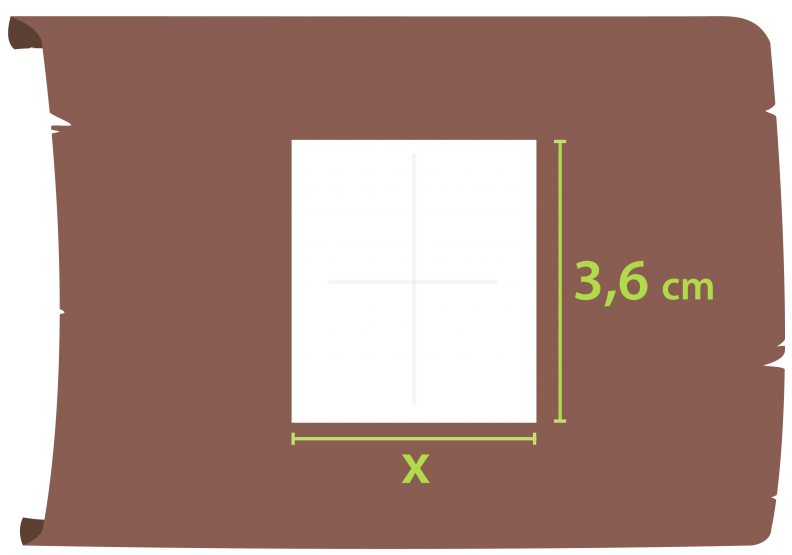
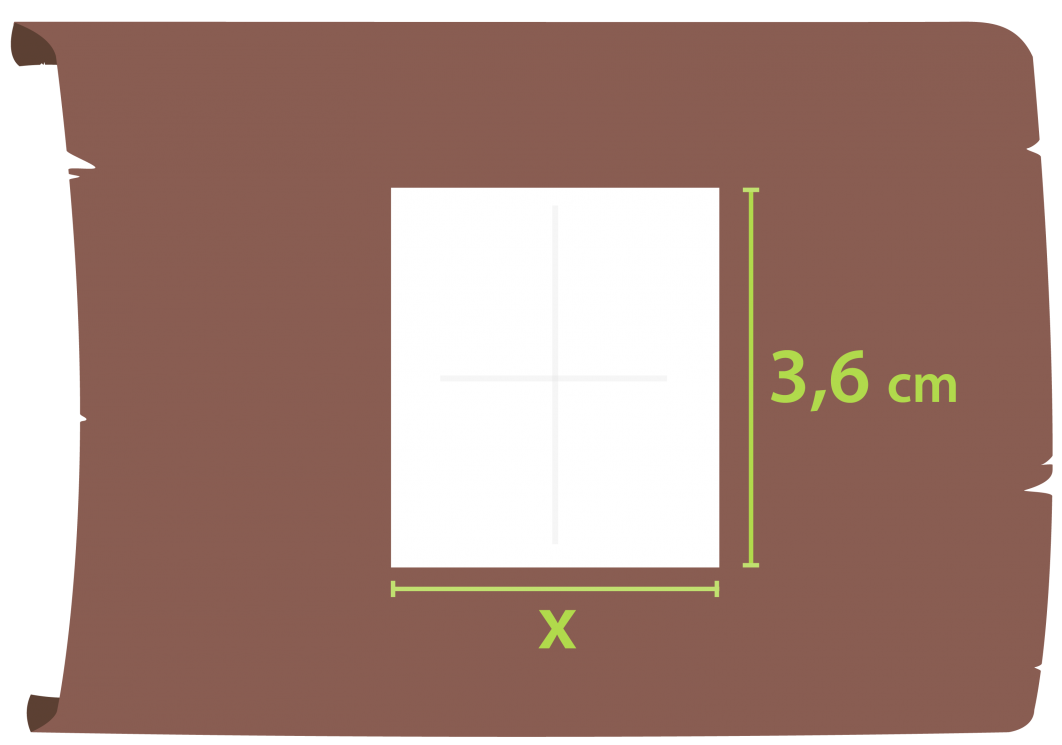
San­te­ri on piir­tä­nyt ma­jan ra­ken­nus­pii­rus­tuk­set.

Klik­kaa kuva suu­rem­mak­si!

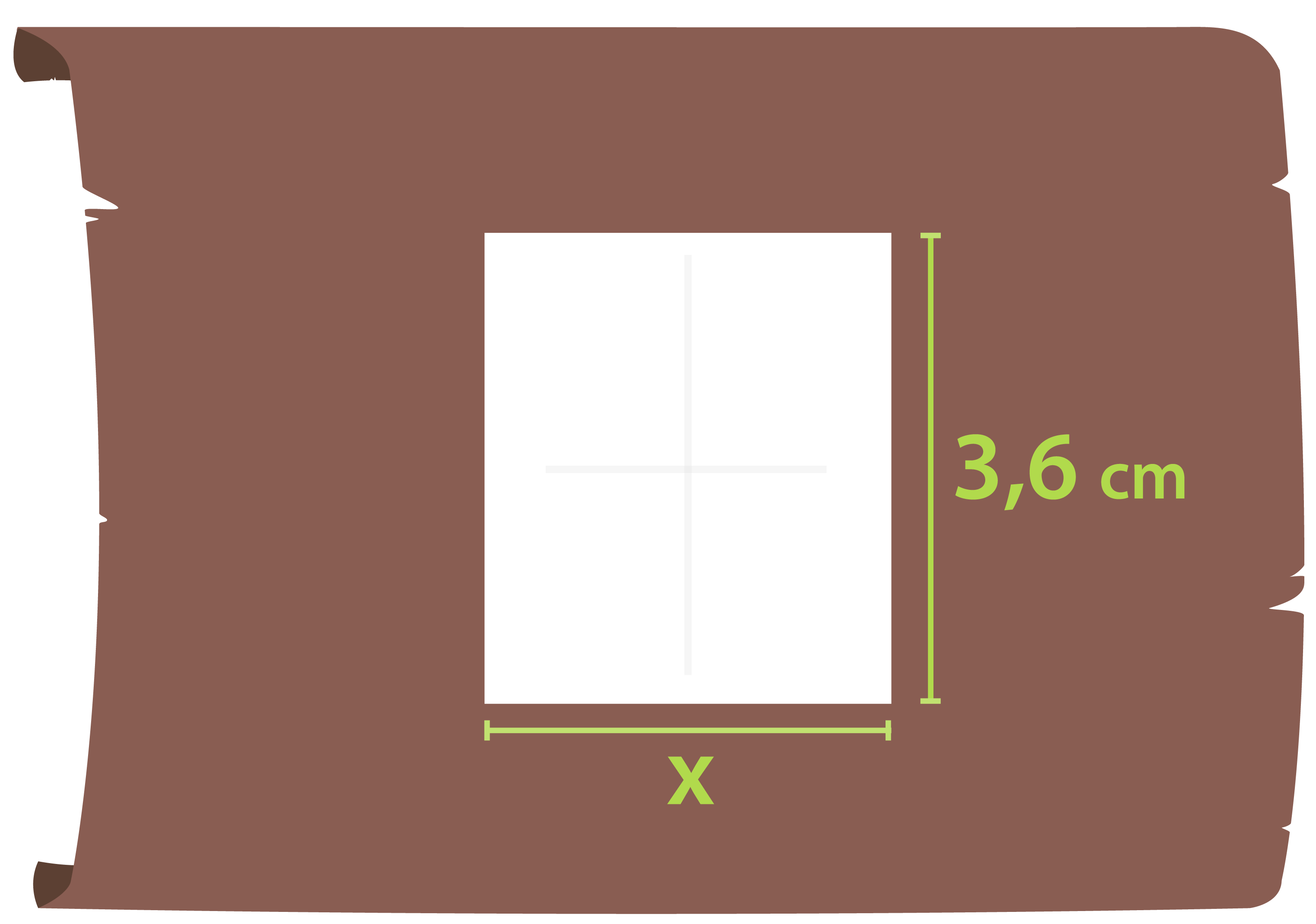
Ma­jan lat­tia on suo­ra­kul­mio, jon­ka si­vu­jen pi­tuu­det ovat pii­rus­tuk­ses­sa 2,5 cm ja 1,5 cm. Luon­nol­li­ses­sa koos­sa lat­ti­an pi­tem­pi sivu on 3,6 m. Mikä on ly­hem­män si­vun pi­tuus?

Ratkaisu:

En­nen kuin ver­ran­toa voi­daan käyt­tää, on mi­tat esi­tet­tä­vä sa­mois­sa yk­si­köis­sä.

2,5 cm  = 0,025 m ja 1,5 cm = 0,015 m.

Jot­ta luon­nol­li­ses­sa koos­sa ole­va lat­tia oli­si ra­ken­nus­pii­rus­tuk­sen mu­kai­nen, on vas­tin­si­vu­jen pi­tuuk­sien suh­tei­den ol­ta­va sa­mat.

Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Lat­ti­an ly­hy­em­män si­vun pi­tuus on 2,2 m.

Huom! Ver­ran­to voi­daan kir­joit­taa myös si­ten, että las­ke­taan ku­vi­oi­den pi­tuuk­sien suh­teet ja ver­ra­taan nii­tä toi­sen ku­vi­on vas­taa­vien pi­tuuk­sien suh­tee­seen. Sa­maan tu­lok­seen siis pää­dy­tään kir­joit­ta­mal­la edel­li­nen ver­ran­to muo­dos­sa

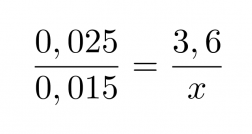
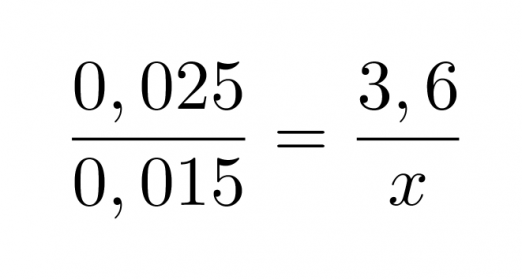
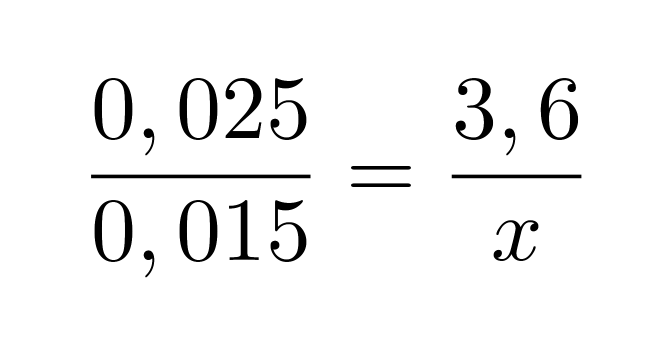
Klik­kaa kuva suu­rem­mak­si!