2. Mittakaava

Kart­ta on pie­nen­net­ty kuva alu­ees­ta, sii­nä muo­dot ovat sa­mat kuin to­del­li­suu­des­sa, mut­ta koko on eri­lai­nen. Jot­ta kar­tal­ta pys­tyt­täi­siin mää­rit­tä­mään väli­mat­kan to­del­li­nen pi­tuus, on sii­tä löy­dyt­tä­vä tie­dot käy­te­tys­tä mit­ta­kaa­vas­ta. Jos taas ha­lu­taan tut­kia tar­kem­min esi­mer­kik­si pien­e­li­öi­den yk­si­tyis­koh­tia, ku­vi­os­ta teh­dään suu­ren­nos. Pie­nen­tä­mi­nen ja suu­ren­ta­mi­nen ovat yh­den­muo­toi­suus­ku­vauk­sia, niis­sä ku­vi­on muo­to säi­lyy, mut­ta koko muut­tuu.

Mit­ta­kaa­va il­mais­taan ta­val­li­ses­ti muo­dos­sa, jos­sa edel­li­nen tai jäl­kim­mäi­nen jä­sen on yksi. Pie­nen­nök­sis­sä suh­det­ta il­mai­se­van kak­sois­pis­teen edes­sä on yk­kö­nen. Suu­ren­nok­sis­sa puo­les­taan yk­kö­nen on mit­ta­kaa­van mer­kin­näs­sä kak­sois­pis­teen jäl­jes­sä.

Kos­ka mit­ta­kaa­va on suh­de­luku, jol­la ei ole yk­sik­köä, voi­daan tar­kas­te­lu­yk­si­köt va­li­ta va­paas­ti. Suh­tee­seen on kui­ten­kin si­joi­tet­ta­va lu­vut sa­mois­sa yk­si­köis­sä. Esi­mer­kik­si kar­tan mit­ta­kaa­va 1 : 1000 voi­daan tul­ki­ta si­ten, että 1 m kar­tal­la vas­taa 1000 m luon­nos­sa tai 1 mm kar­tal­la vas­taa 1000 mm luon­nos­sa. Sent­ti­met­rit ovat kui­ten­kin yleen­sä kar­tal­la käy­tän­nöl­li­sim­piä.

Esimerkki 1.

Hel­sin­gin opas­kart­ta on teh­ty mit­ta­kaa­vas­sa 1 : 20 000. Mat­ka edus­kun­ta­ta­lol­ta pre­si­den­tin lin­naan Man­ner­hei­min­tie­tä ja Esp­la­na­dia pit­kin on kar­tal­ta mi­tat­tu­na 8 cm. Kuin­ka pit­kä mat­ka on to­del­li­suu­des­sa?

Ratkaisu:

Suh­de 1 : 20 000 tar­koit­taa, että yh­den sent­ti­met­rin mat­ka kar­tal­la vas­taa luon­nos­sa 20 000 cm:n mat­kaa. 8 cm:n mat­ka kar­tal­la on täl­löin luon­nos­sa .

Vas­taus: Mat­ka on 1,6 km pit­kä.

Esimerkki 2.

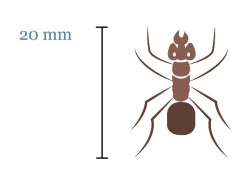
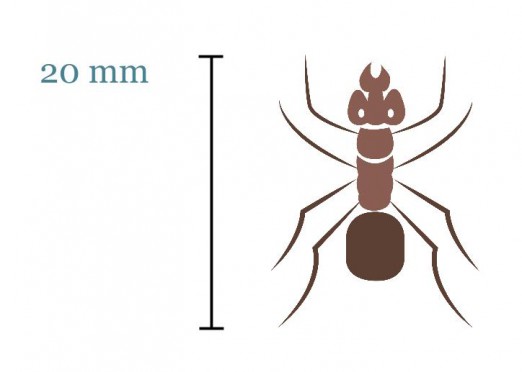
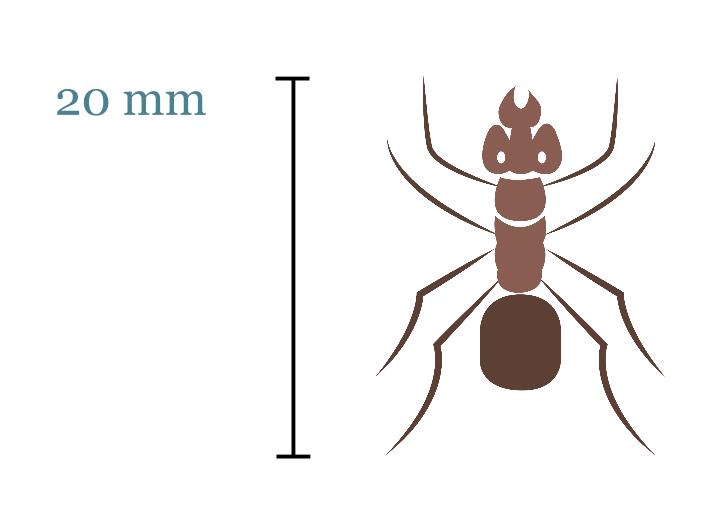
Las­ke­taan muu­ra­hai­sen to­del­li­nen koko, kun kuva on mit­ta­kaa­vas­sa 6 : 1.

Klik­kaa kuva suu­rem­mak­si!

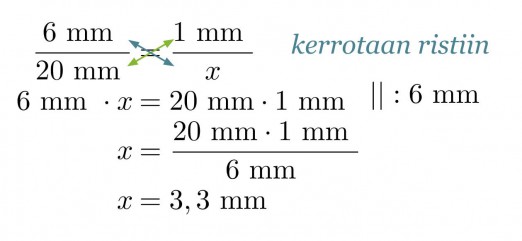
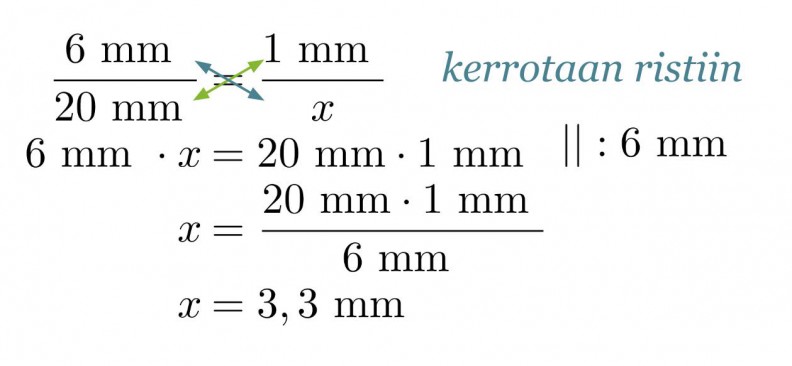
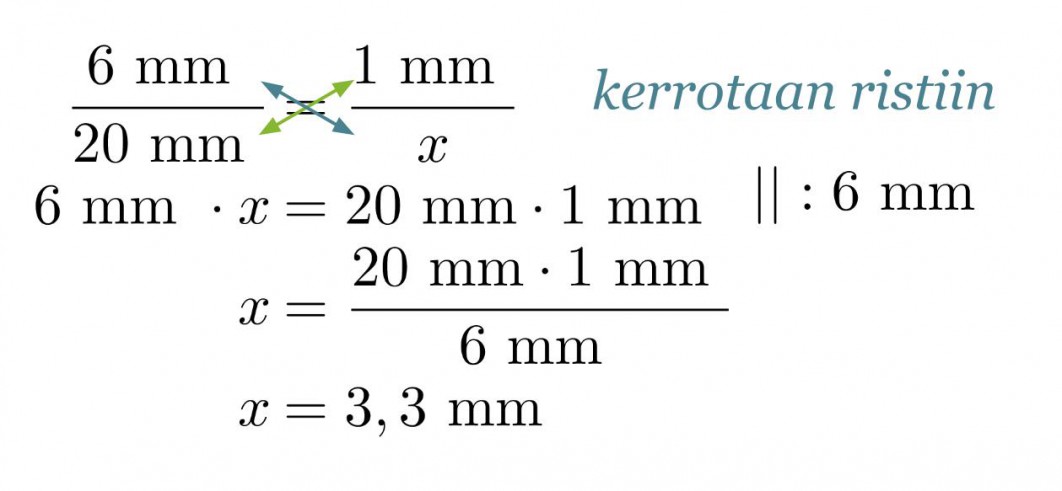
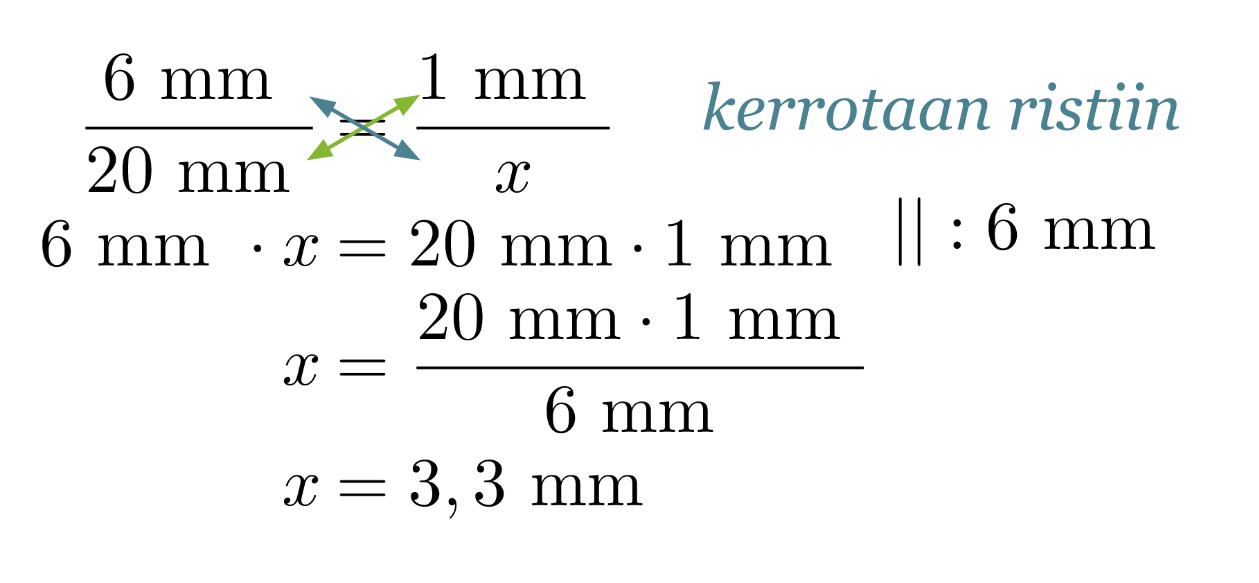
Muu­ra­hai­sen kes­ki­osan pi­tuus ku­vas­sa on 20 mm. To­del­li­nen pi­tuus saa­daan ver­ran­non avul­la.

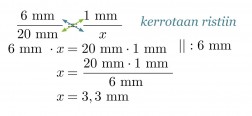
Klik­kaa kuva suu­rem­mak­si!

Esimerkki 3.

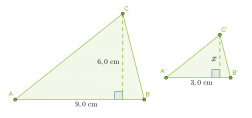
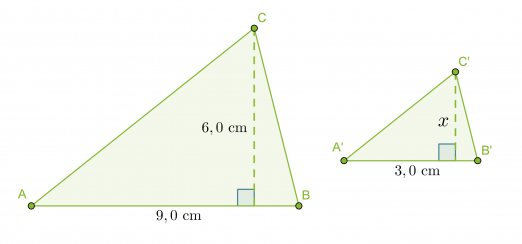
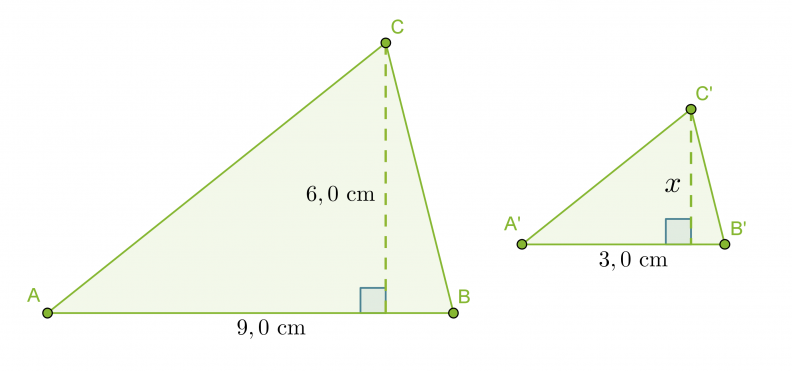
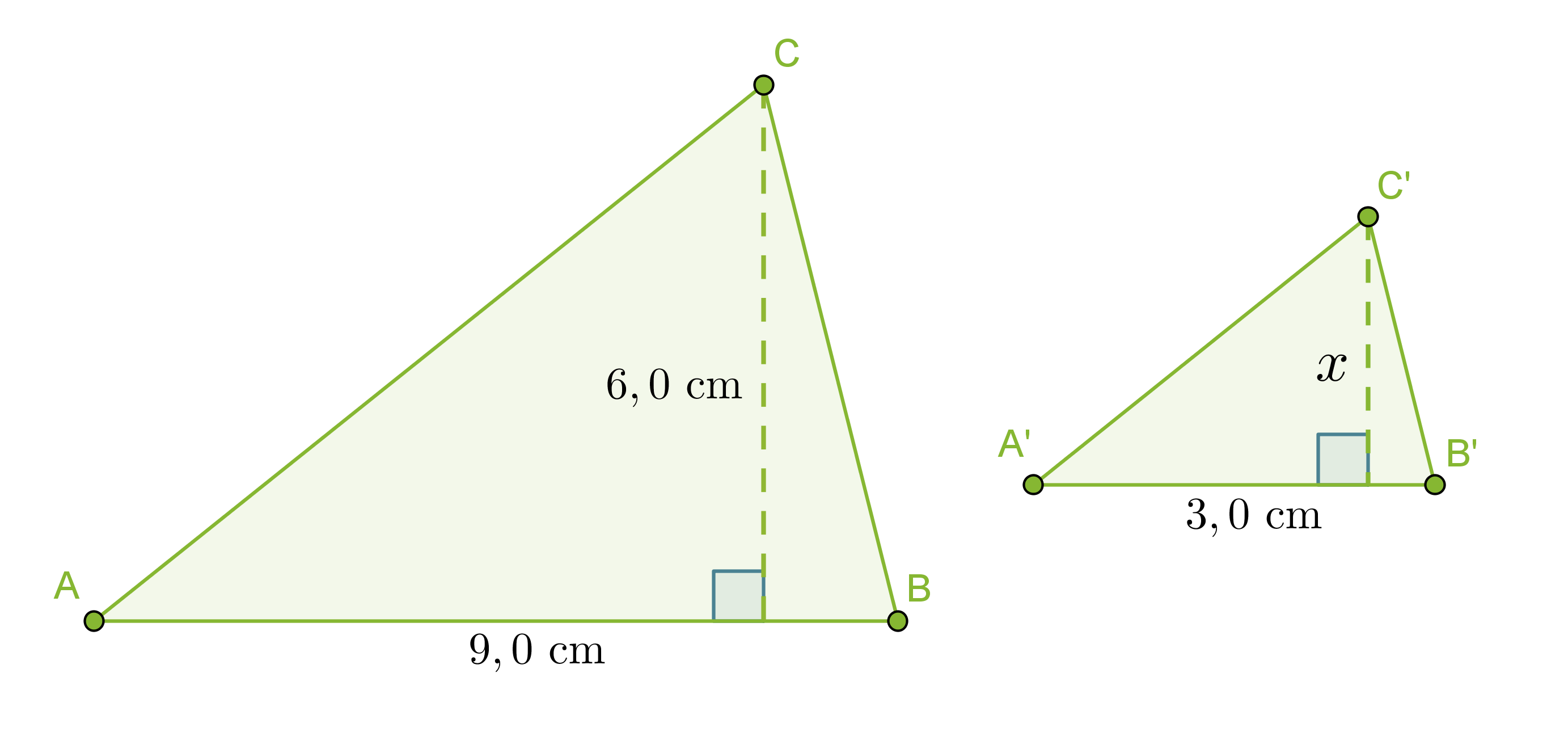
Kol­mi­ot ABC ja A´B´C´ ovat yh­den­muo­toi­set. Mikä on käy­tet­ty mit­ta­kaa­va ja kol­mi­on A’B’C kor­keus?

Klik­kaa kuva suu­rem­mak­si!

Ratkaisu:

Mit­ta­kaa­va on vas­tin­si­vu­jen suh­de AB : A’B’ = 9,0 cm : 3,0 cm = 3 : 1

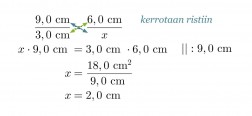
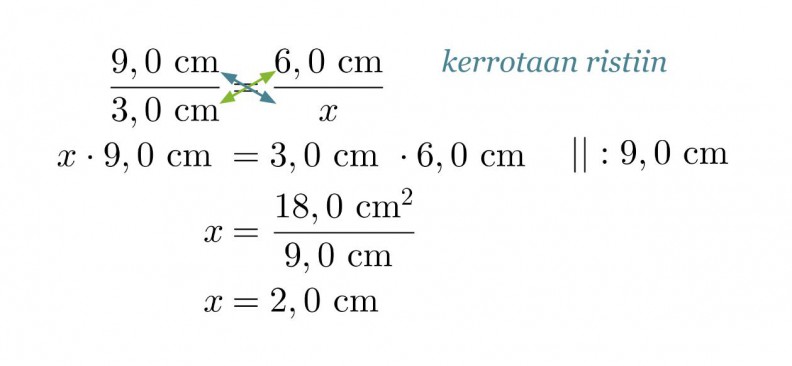
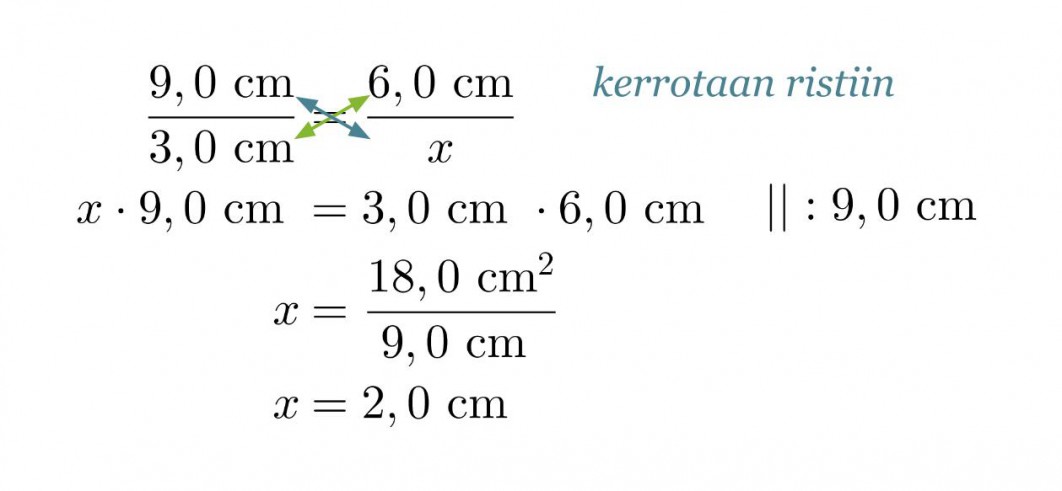
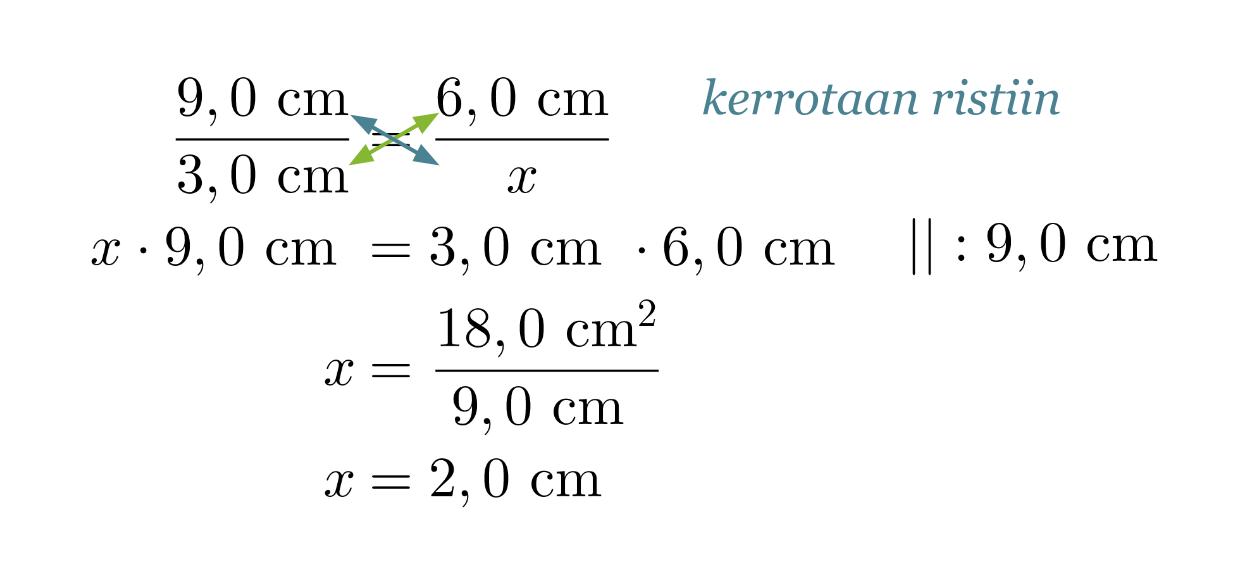
Kos­ka vas­tin­si­vu­jen suh­de säi­lyy sa­ma­na, voi­daan muo­dos­taa ver­ran­to kor­keu­den rat­kai­se­mi­sek­si.

Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Mit­ta­kaa­va on 3 : 1 ja pie­nem­män kol­mi­on kor­keus on 2,0 cm.