3. Kolmioiden yhdenmuotoisuus
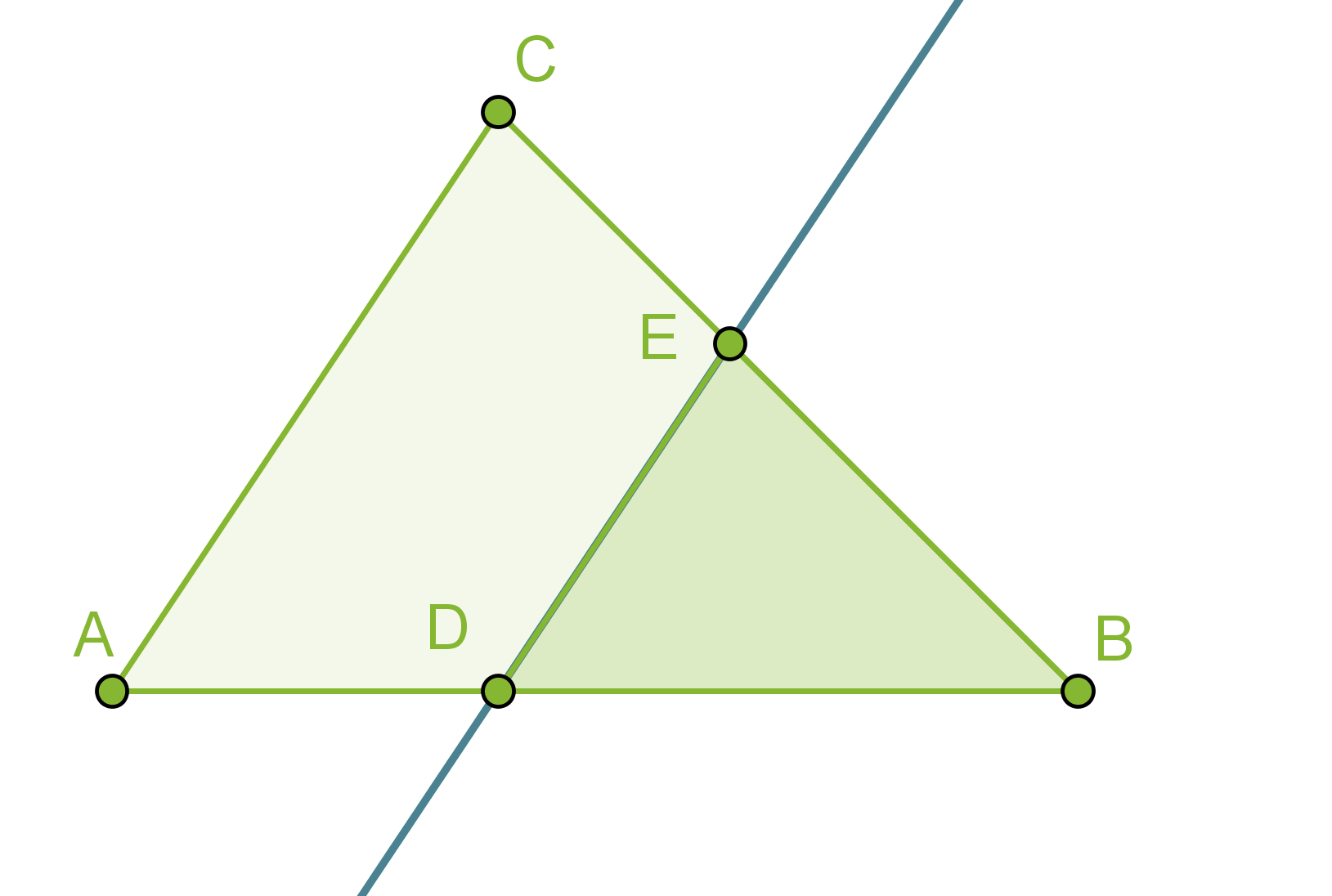
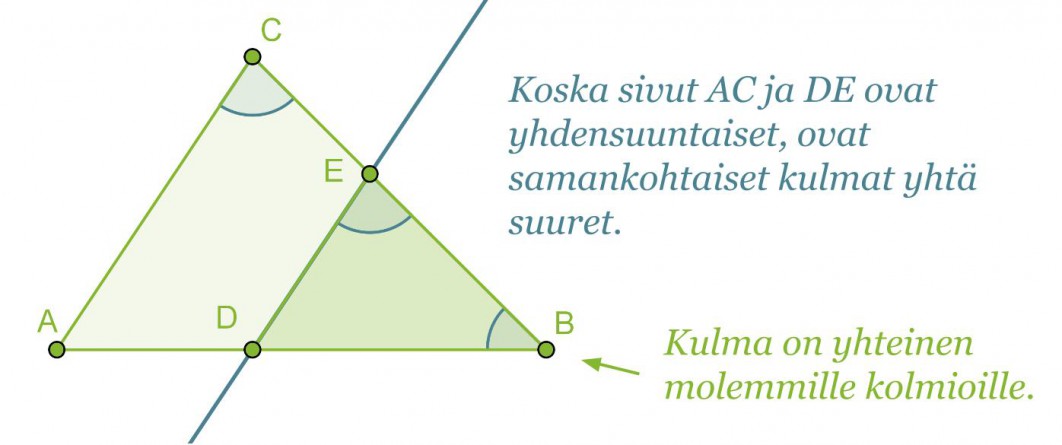
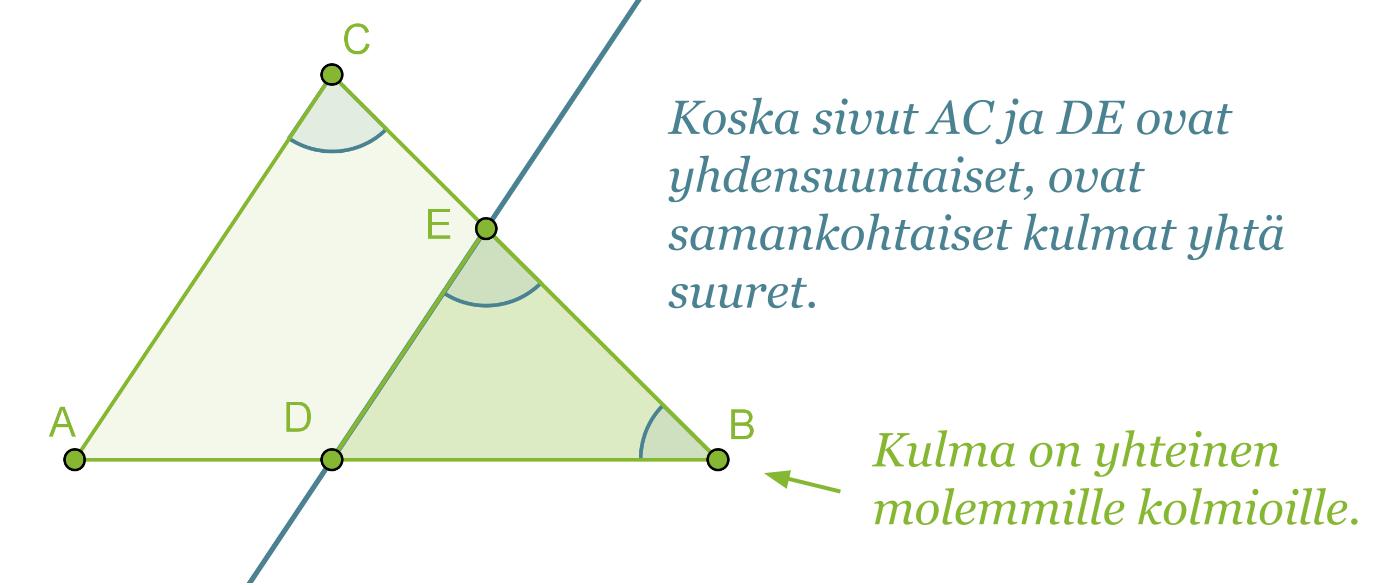
Jos kolmio jaetaan kahteen osaan jollakin kolmion sivun kanssa yhdensuuntaisella suoralla, muodostuu alkuperäisen kolmion kanssa yhdenmuotoinen kolmio eli ABC~DBE.
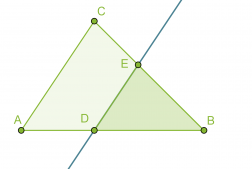
Klikkaa kuva suuremmaksi!
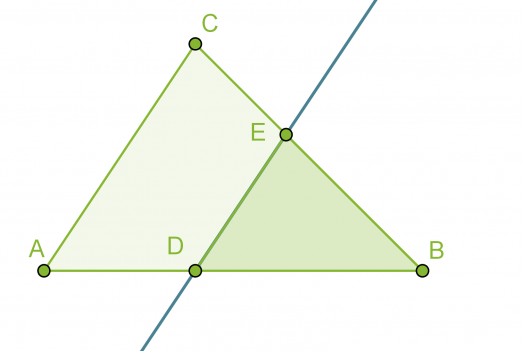
Klikkaa kuva suuremmaksi!
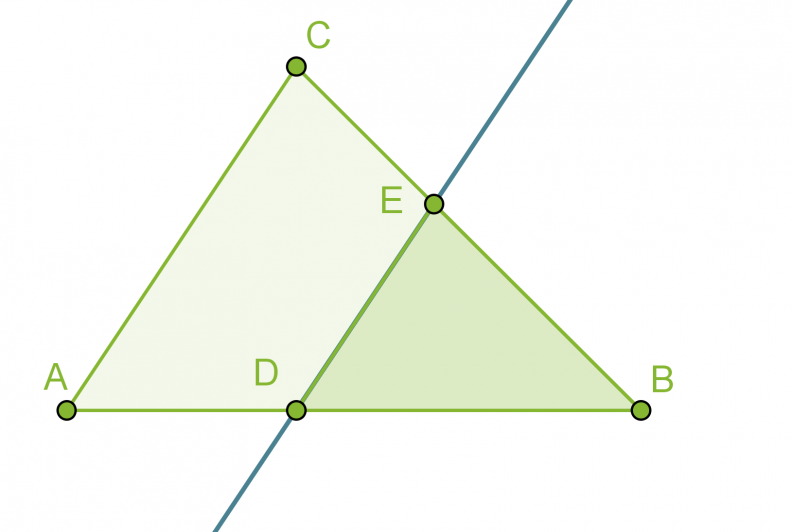
Klikkaa kuva suuremmaksi!
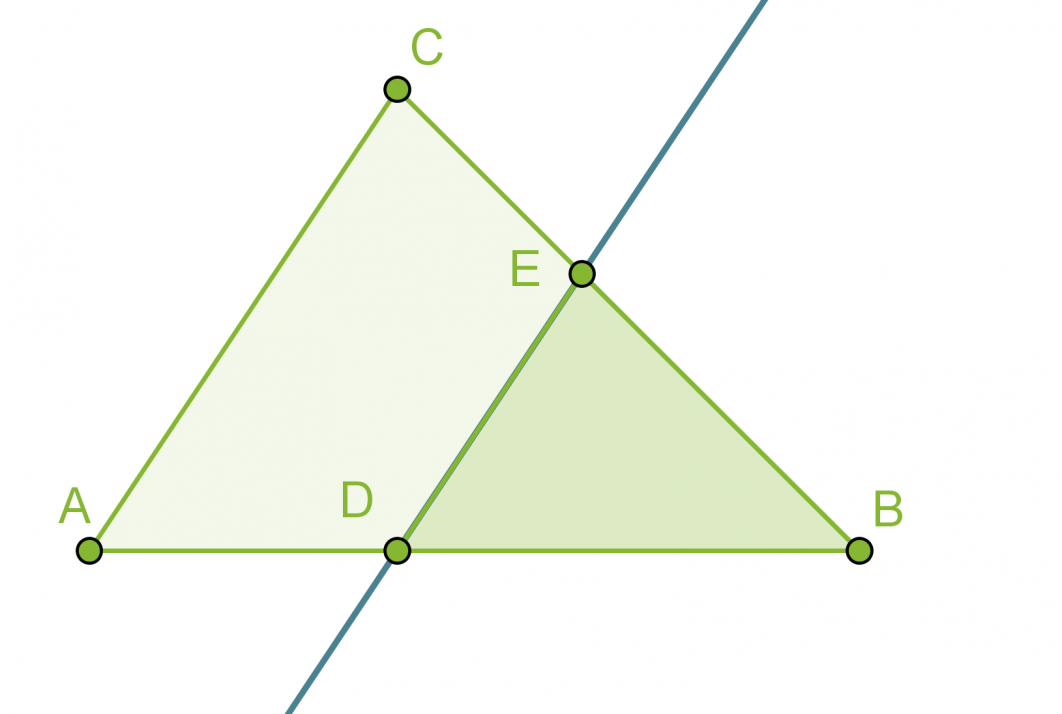
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
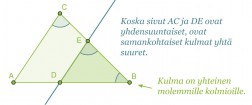
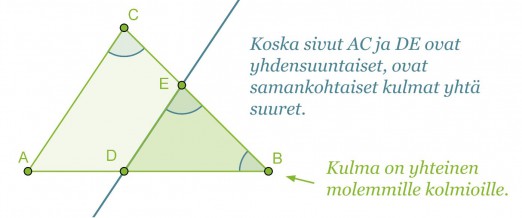
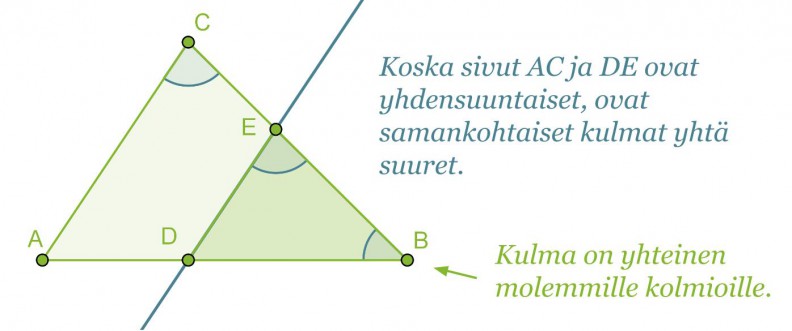
Kolmiot ABC ja DBE ovat keskenään yhdenmuotoiset, jos niiden kaikki vastinkulmat ovat keskenään yhtä suuria.
Yhdenmuotoisuustarkasteluissa kuitenkin riittää osoittaa ainoastaan kaksi vastinkulmista yhtäsuuriksi. Koska kolmion kulmien summa on 180°, on kolmansienkin vastinkulmien oltava yhtäsuuret.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kun kolmioiden yhdenmuotoisuus on todettu, voidaan kaikkia kolmion vastinsivuja verrata keskenään ja pituuksien suhteeksi saadaan sivuparista riippumatta sama arvo
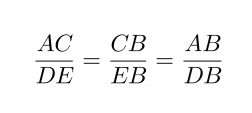
Klikkaa kuva suuremmaksi!
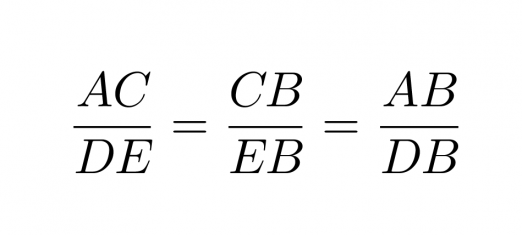
Klikkaa kuva suuremmaksi!
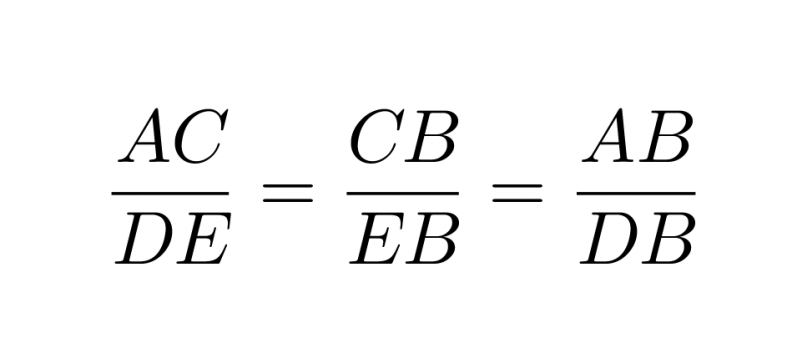
Klikkaa kuva suuremmaksi!
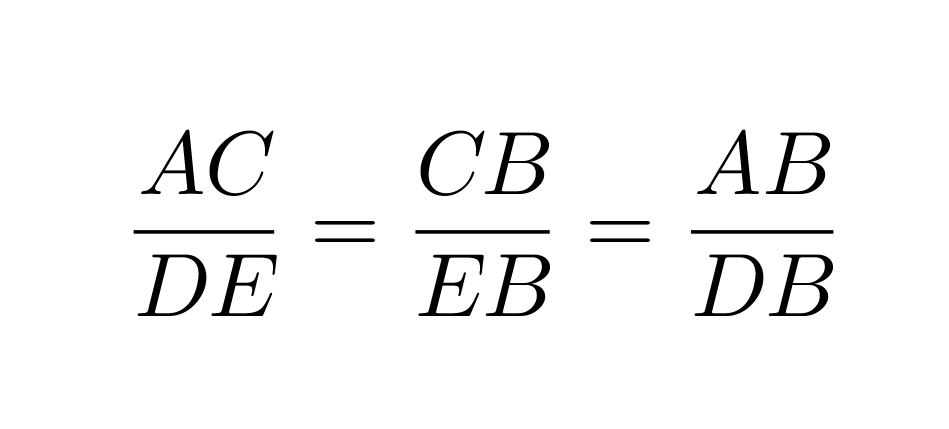
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
1,7 m pituisen henkilön varjon pituus on 2,5 m. Samanaikaisesti Eiffeltornin varjon pituus on 441 m. Kuinka korkea torni on?

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkissä muodostuu kaksi yhdenmuotoista kolmiota, sillä valon säteen ja maan välinen kulma on kummassakin tapauksessa sama. Lisäksi Eiffeltorni ja henkilö ovat kohtisuorassa maata vasten.
Eiffeltornin ja henkilön pituuksien suhde on sama kuin varjojen pituuksien suhde, joten saamme verrannon.
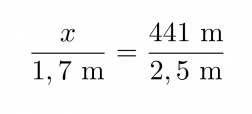
Klikkaa kuva suuremmaksi!
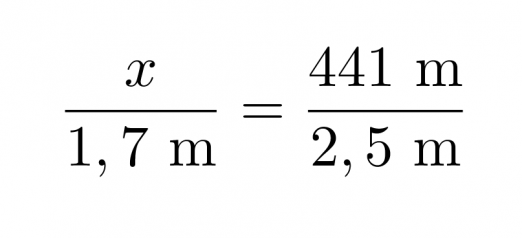
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
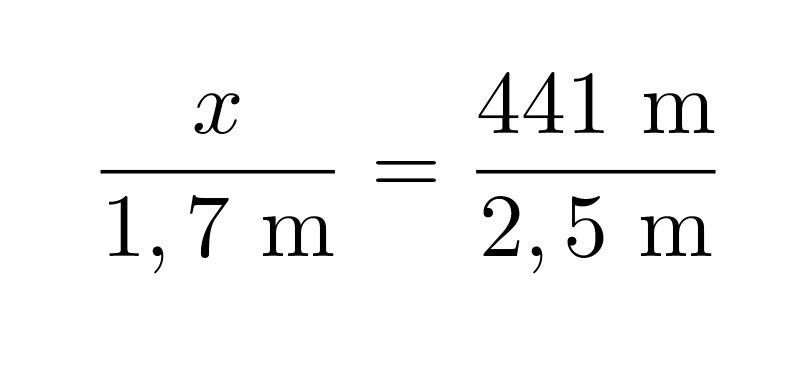
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaistaan tämä ristiin kertomalla:
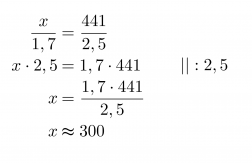
Klikkaa kuva suuremmaksi!
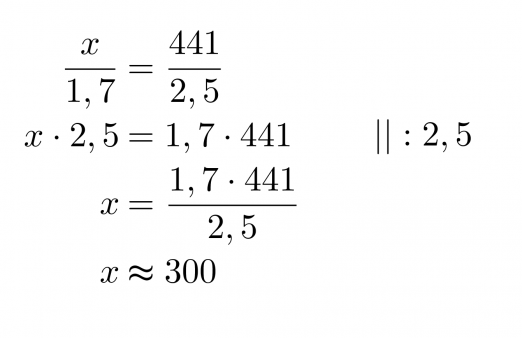
Klikkaa kuva suuremmaksi!
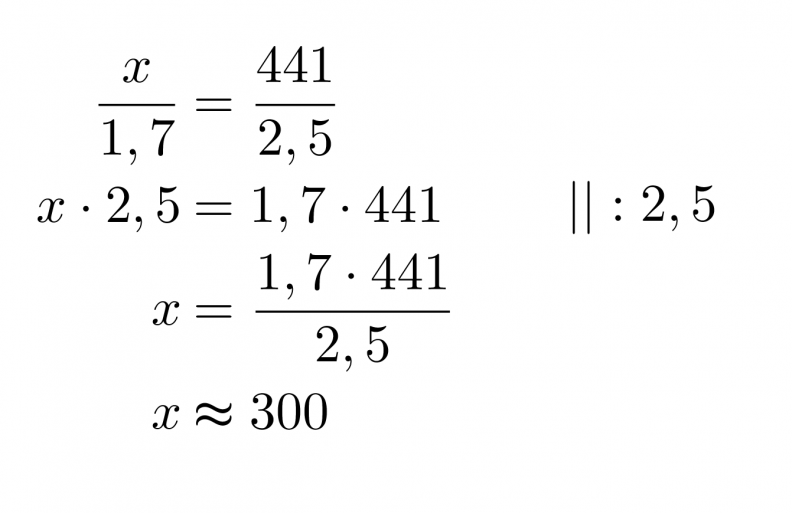
Klikkaa kuva suuremmaksi!
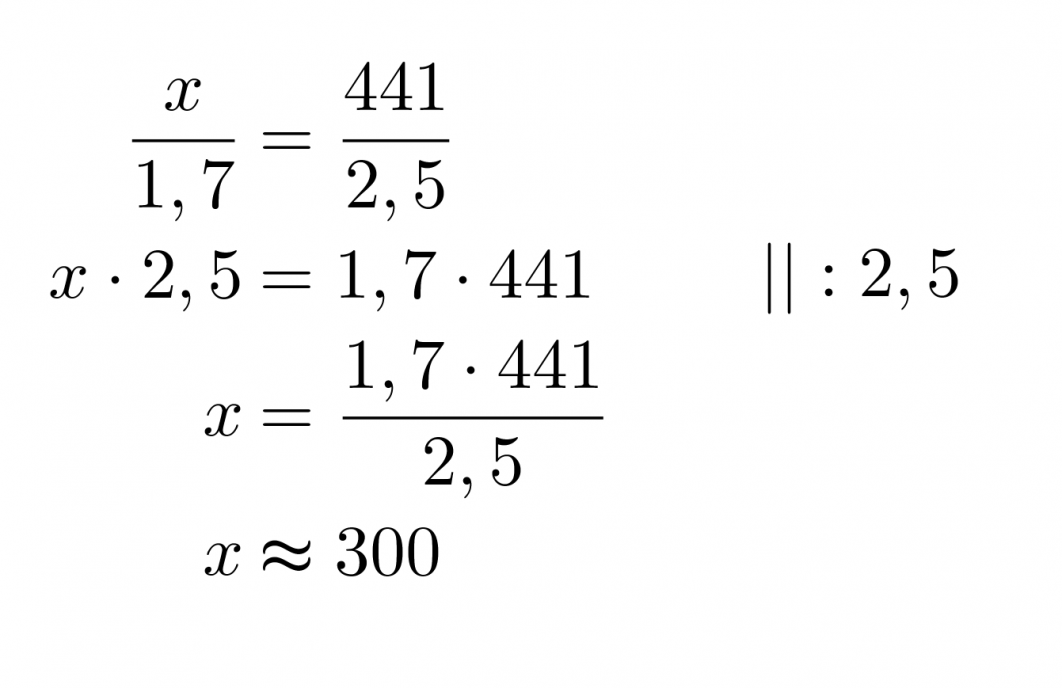
Klikkaa kuva suuremmaksi!
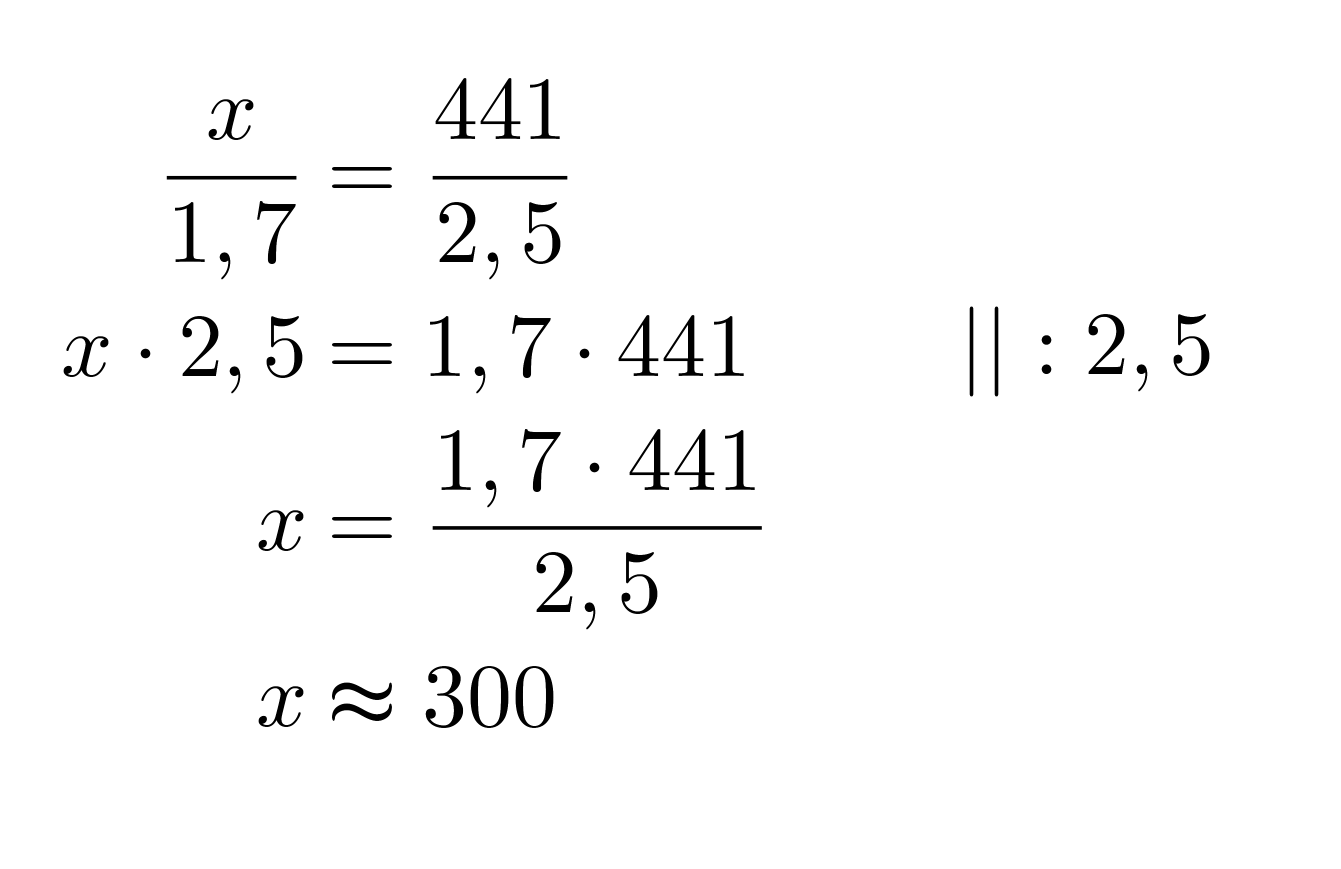
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Eiffeltornin korkeus on noin 300 m.
Avoin matematiikka 8Osio 3: Tasogeometriaa5.6.2014