4. Kultainen leikkaus*
Kultainen leikkaus eli kultainen suhde saadaan, kun jana jaetaan kahteen osaan a ja b siten, että lyhyemmän osan suhde pidempään osaan on sama kuin pidemmän osan suhde koko janaan.
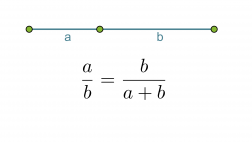
Klikkaa kuva suuremmaksi!
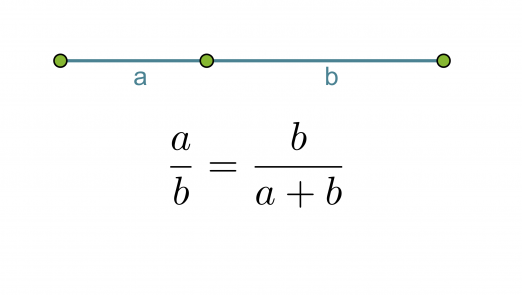
Klikkaa kuva suuremmaksi!
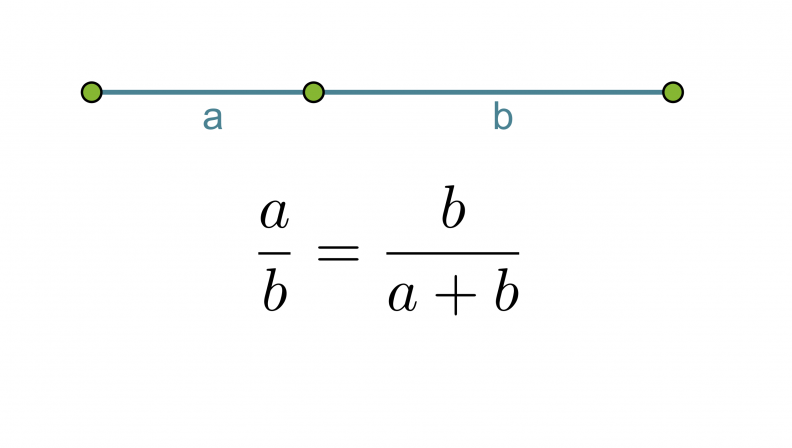
Klikkaa kuva suuremmaksi!
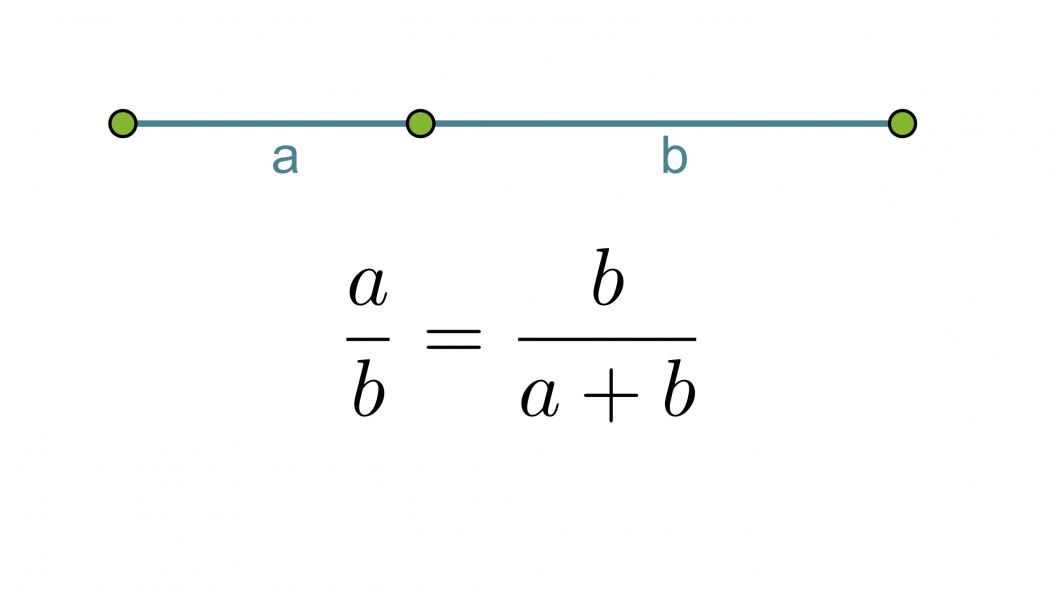
Klikkaa kuva suuremmaksi!
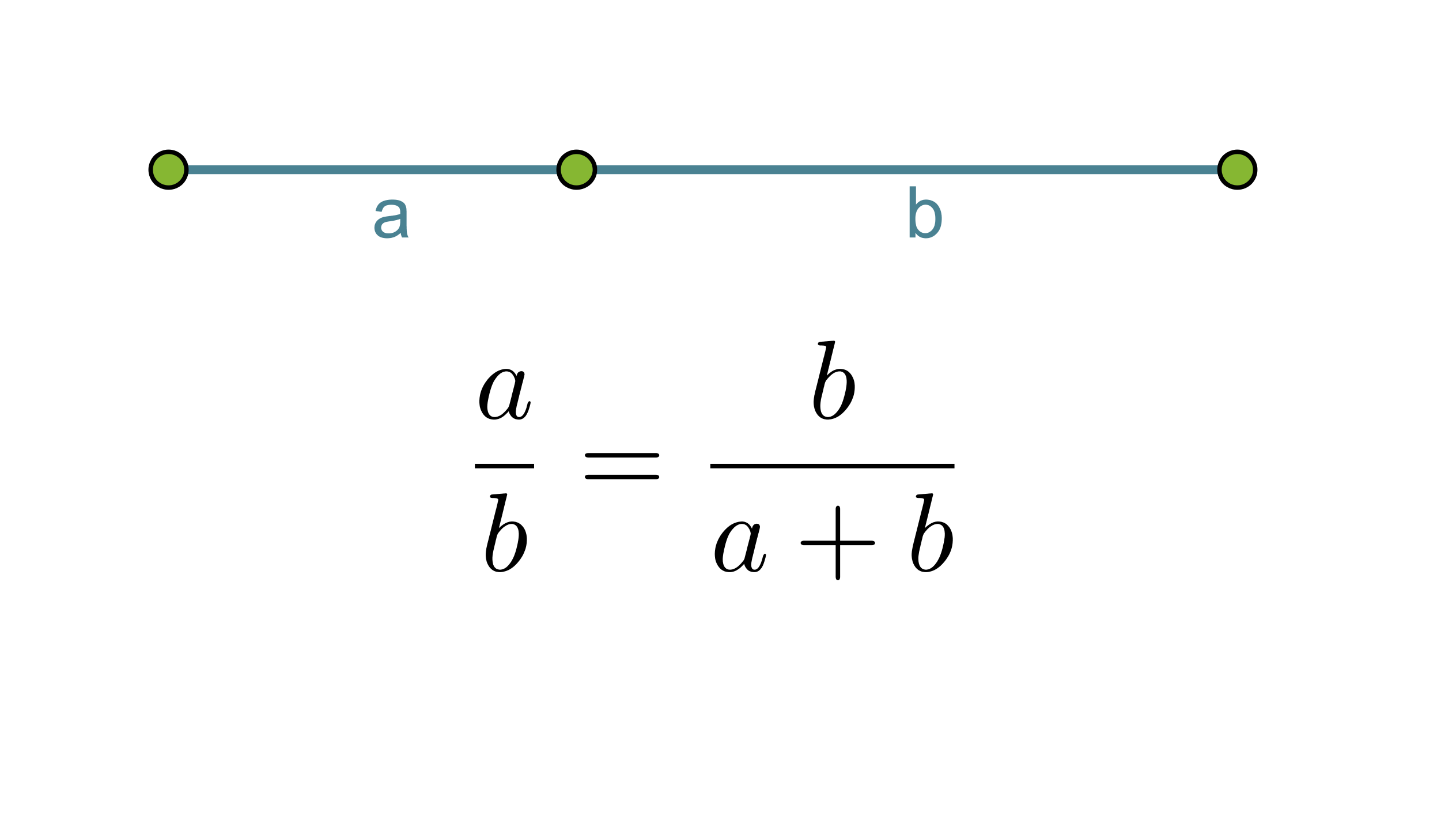
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Yleisesti kultaisen leikkauksen lukuarvona käytetään suhteen käänteisarvoa
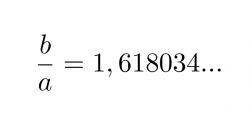
Klikkaa kuva suuremmaksi!
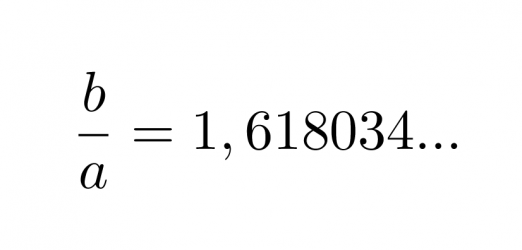
Klikkaa kuva suuremmaksi!
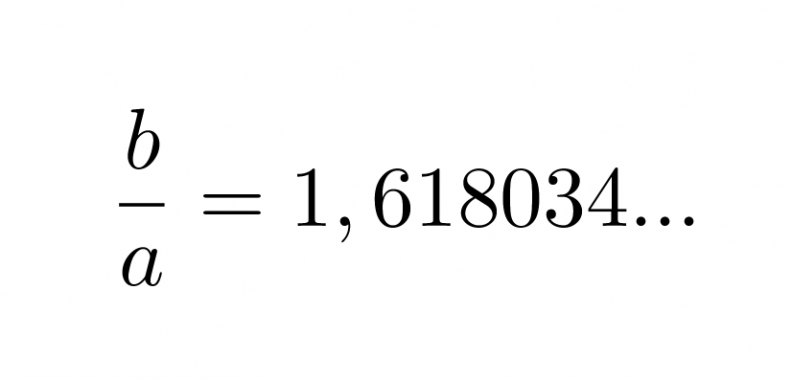
Klikkaa kuva suuremmaksi!
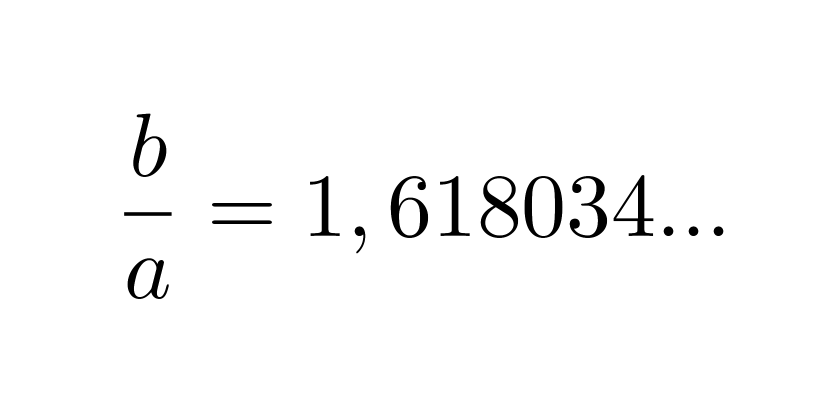
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
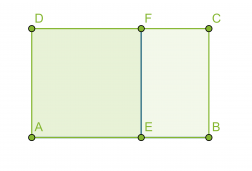
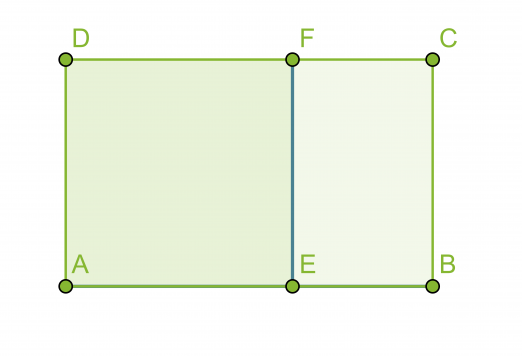
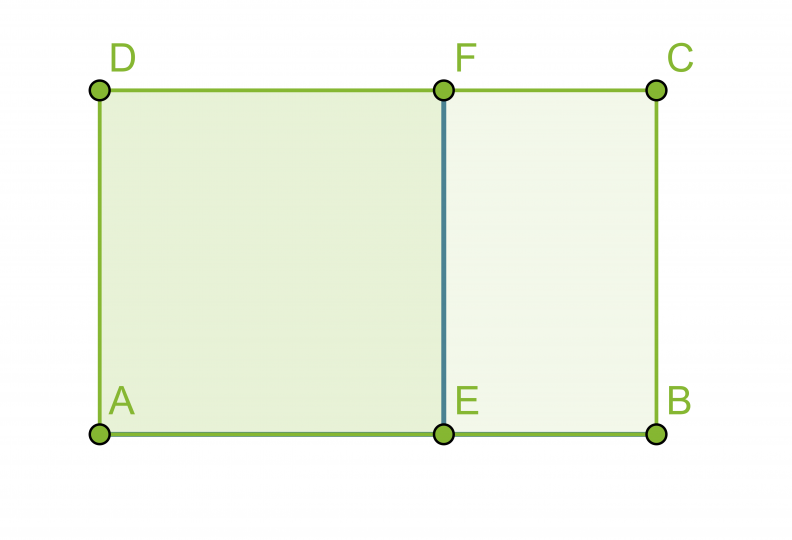
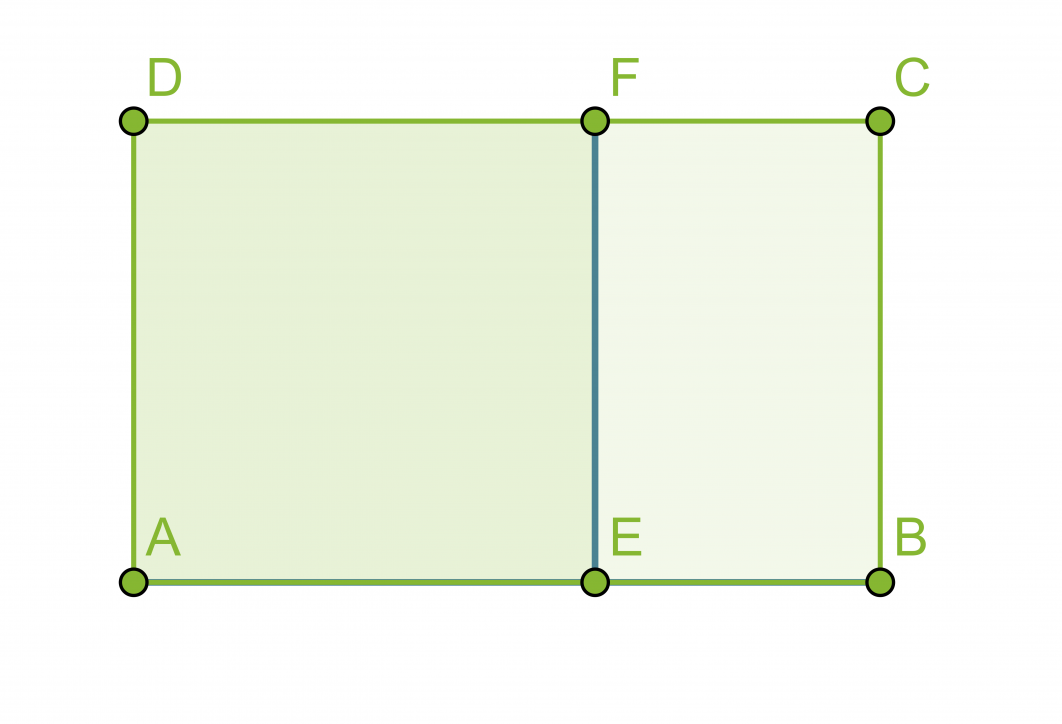
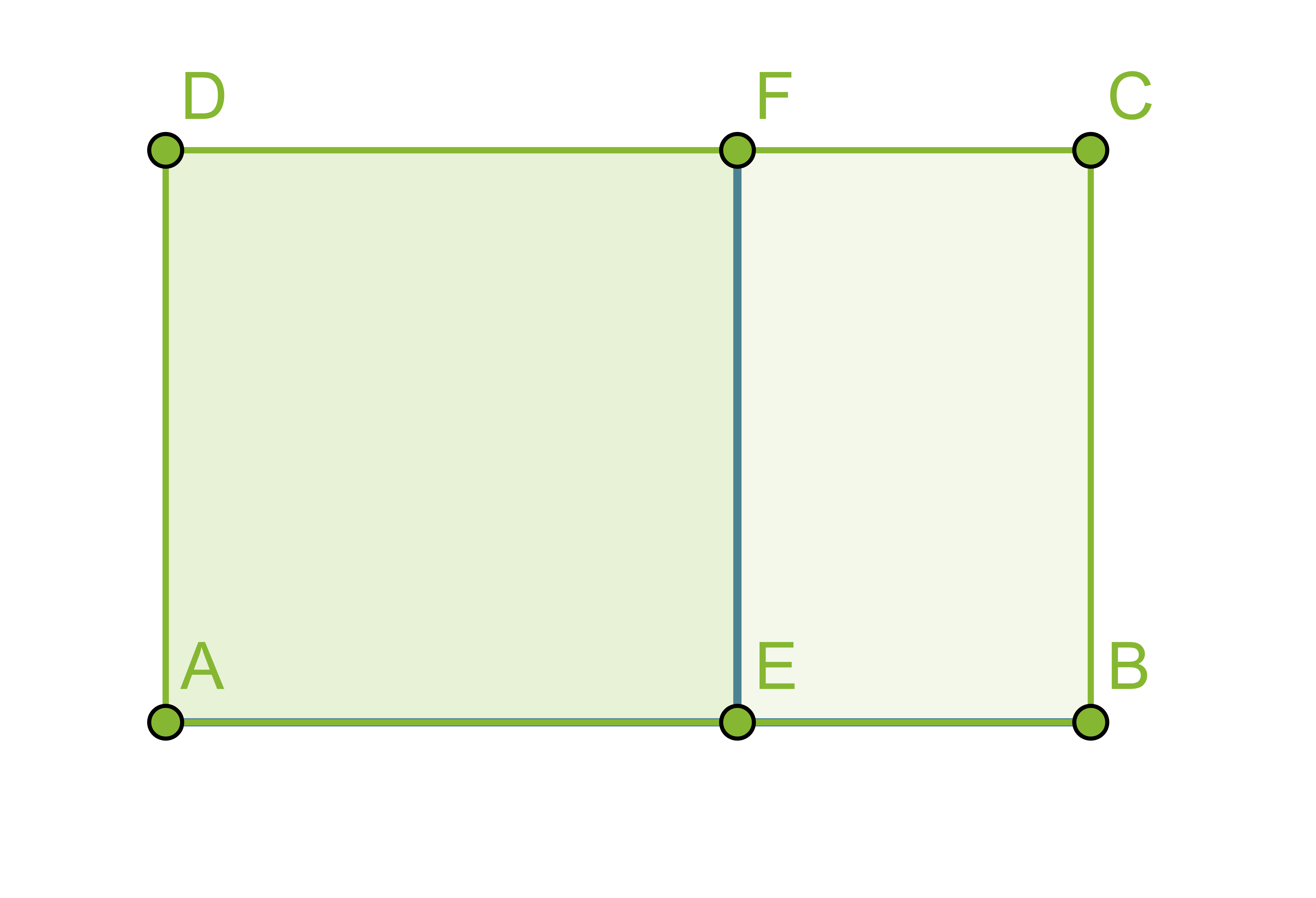
Jos suorakulmio jaetaan kahteen osaan jollakin suorakulmion sivun kanssa yhdensuuntaisella suoralla, ei yleensä muodostu alkuperäisen suorakulmion kanssa yhdenmuotoista suorakulmiota. Suorakulmiota sanotaan kultaiseksi suorakulmioksi, jos se voidaan jakaa neliöksi ja pienemmäksi suorakulmioksi siten, että pienempi suorakulmio on yhdenmuotoinen alkuperäisen suorakulmion kanssa.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suorakulmiot ABCD ja BCFE ovat yhdenmuotoisia, jos niiden sivujen pituudet ovat kultaisessa suhteessa
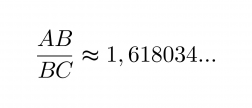
Klikkaa kuva suuremmaksi!
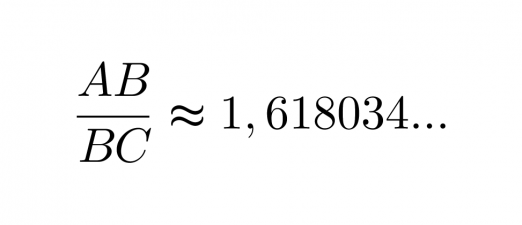
Klikkaa kuva suuremmaksi!
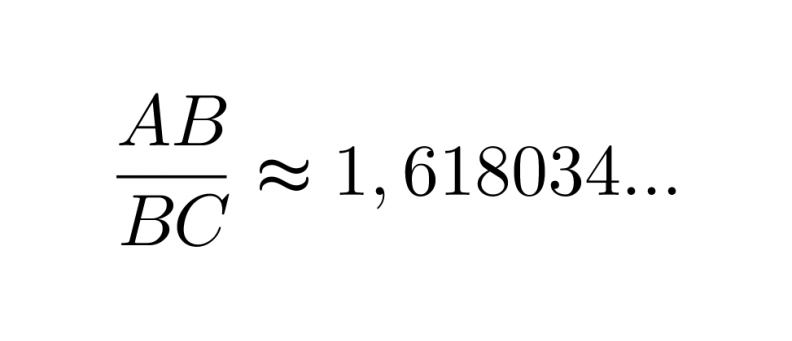
Klikkaa kuva suuremmaksi!
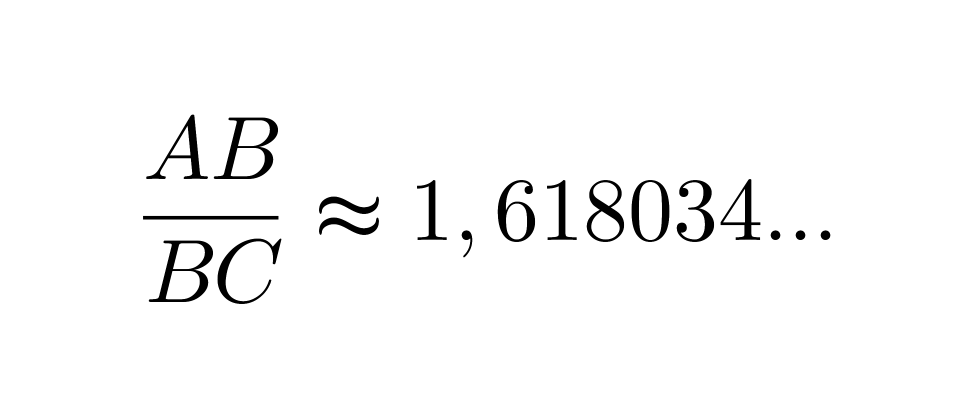
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
Ateenassa olevan Parthenon-temppelin pääty on kultainen suorakulmio. Päädyn korkeus on 19 m. Kuinka leveä pääty on?
Ratkaisu:
Kultaisen suorakulmion pidemmän sivun pituuden suhde lyhyempään sivuun on 1,618034… Olkoon temppelin leveys x. Muodostetaan yhtälö.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Temppelin leveys on noin 31 m.
Avoin matematiikka 8Osio 3: Tasogeometriaa5.6.2014