5. Peilaus suoran suhteen

Jos ha­lu­taan teh­dä jon­kin ku­vi­on kans­sa yh­te­ne­vä ku­vio, käy­te­tään apu­na yh­te­ne­vyys­ku­vauk­sia, joi­ta ovat pei­laus suo­ran suh­teen, pei­laus pis­teen suh­teen, yh­den­suun­tais­siir­to ja kier­to. Koor­di­naa­tis­toa apu­na käyt­tä­en ku­vi­ot ja yh­te­ne­vyys­ku­vauk­set voi­daan esit­tää las­ken­nal­li­ses­ti. Tie­to­kone­gra­fiik­ka pe­rus­tuu tä­hän.

Jos jo­kin yh­te­ne­vyys­ku­vauk­sis­ta pa­laut­taa ku­vi­on täs­mäl­leen sa­maan paik­kaan, jos­sa se alun­pe­rin­kin oli, esiin­tyy ku­vi­ol­la sym­met­ri­aa. Suo­ran suh­teen sym­met­ri­sek­si sa­no­taan ku­vi­o­ta, joka ku­vau­tuu it­sel­leen pei­laus­suo­ran suh­teen. Pei­laus­suo­raa sa­no­taan täl­löin sym­met­ria-ak­se­lik­si.

Klik­kaa kuva suu­rem­mak­si!

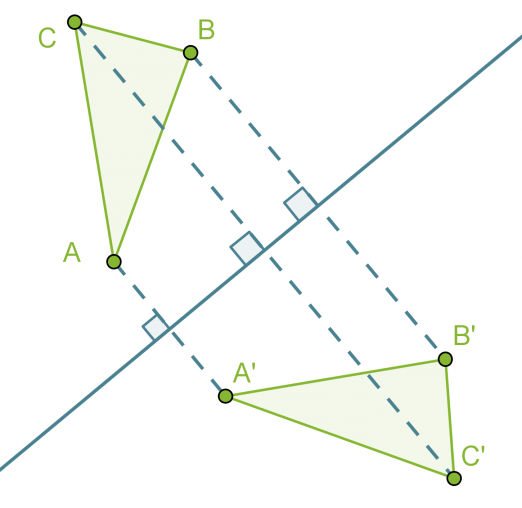
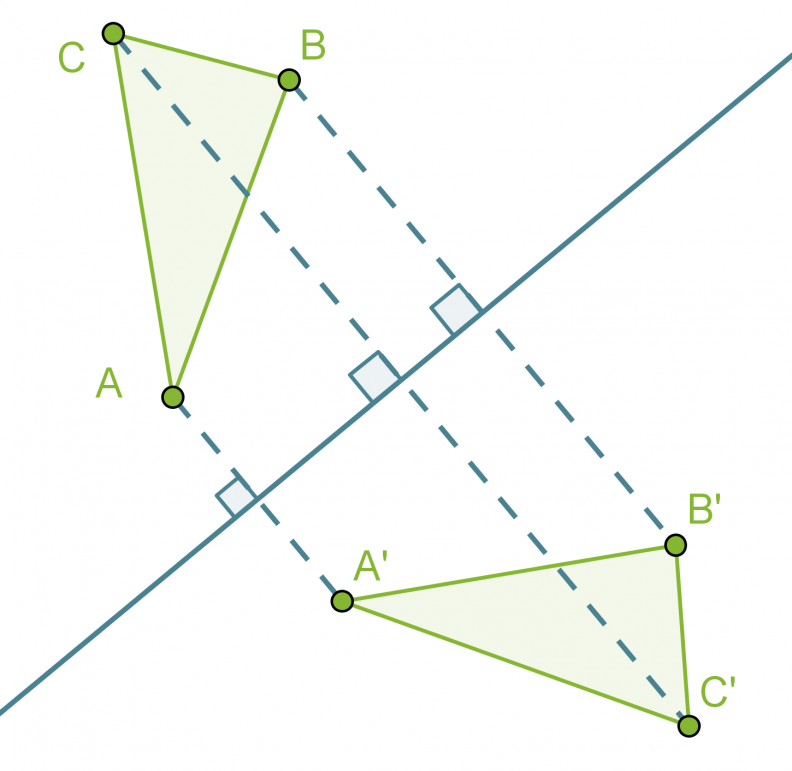
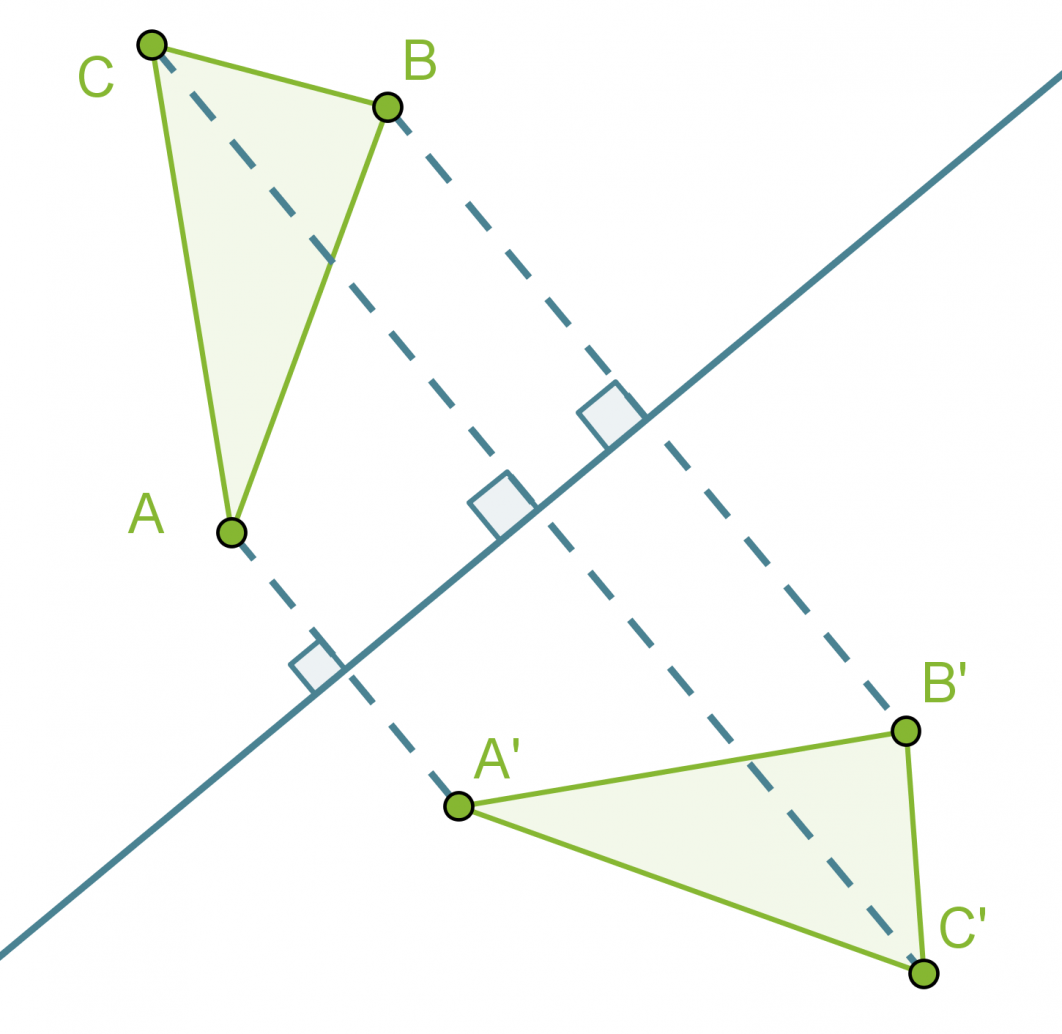
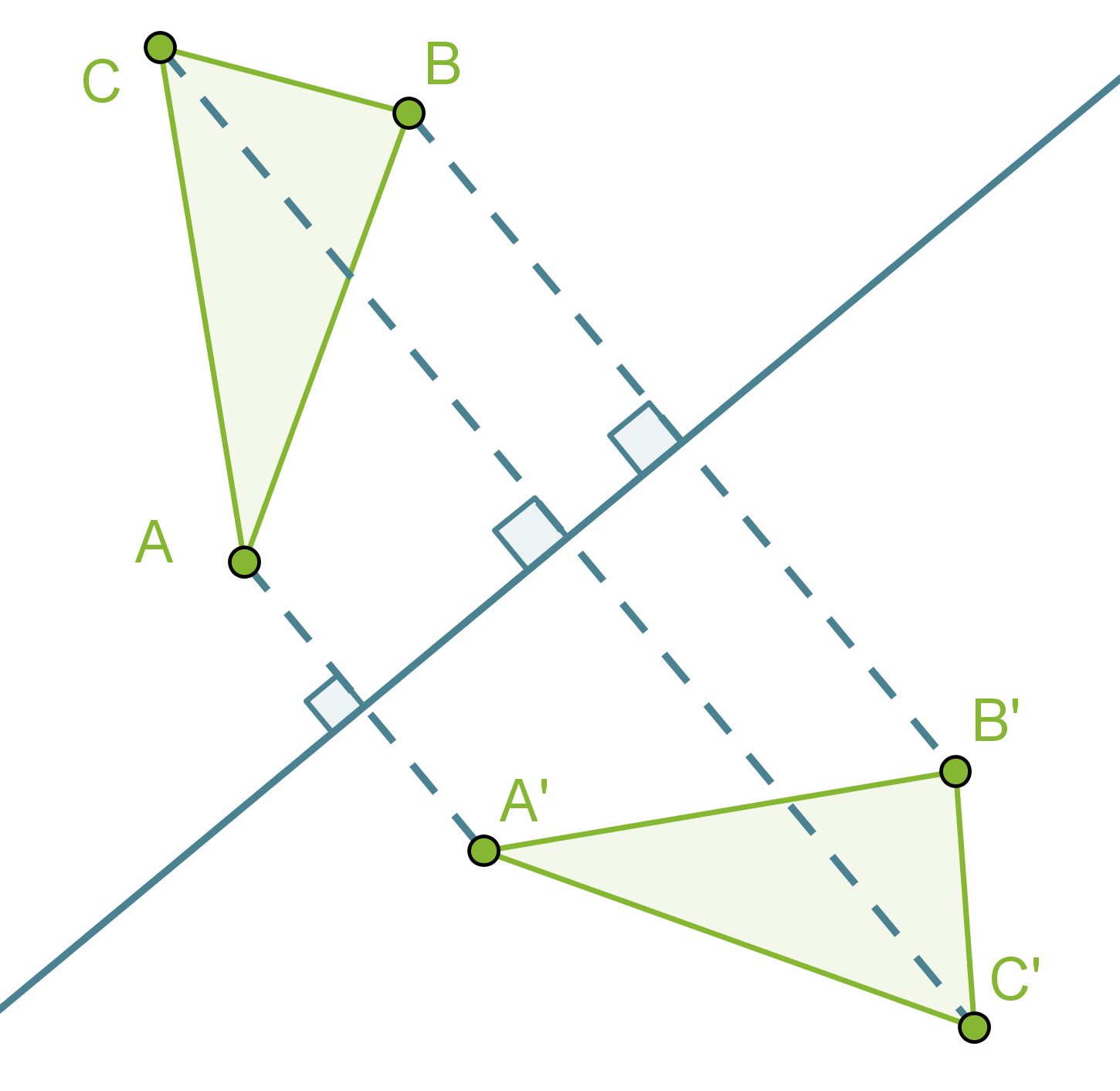
Esimerkki 1.

Pei­la­taan kol­mio ABC suo­ran s suh­teen, saa­daan pei­lat­tu kol­mio A’B’C’, joka on yh­te­ne­vä alku­pe­räi­sen kol­mi­on kans­sa.

Klik­kaa kuva suu­rem­mak­si!

Esimerkki 2.

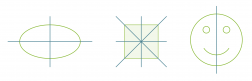
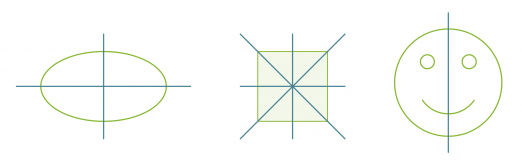
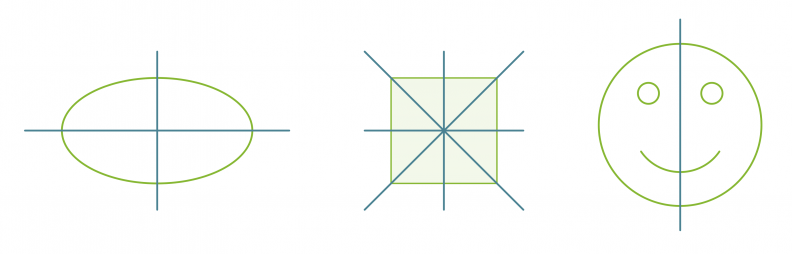
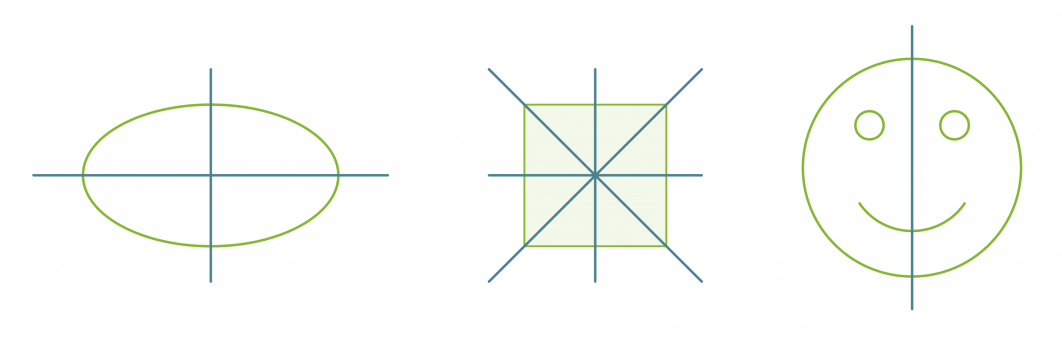
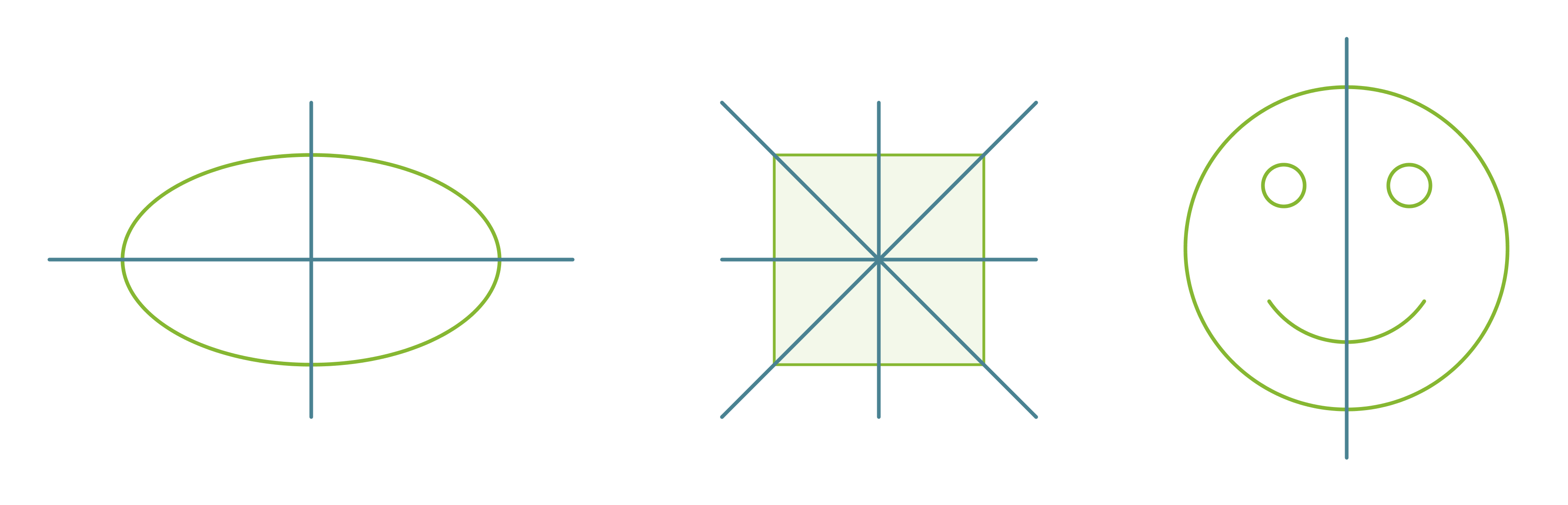
Suo­ran suh­teen sym­met­ri­siä ku­vi­oi­ta ja nii­den sym­met­ria-ak­se­lit.

Klik­kaa kuva suu­rem­mak­si!