7. Kierto ja siirto tasossa
Esimerkki 1.
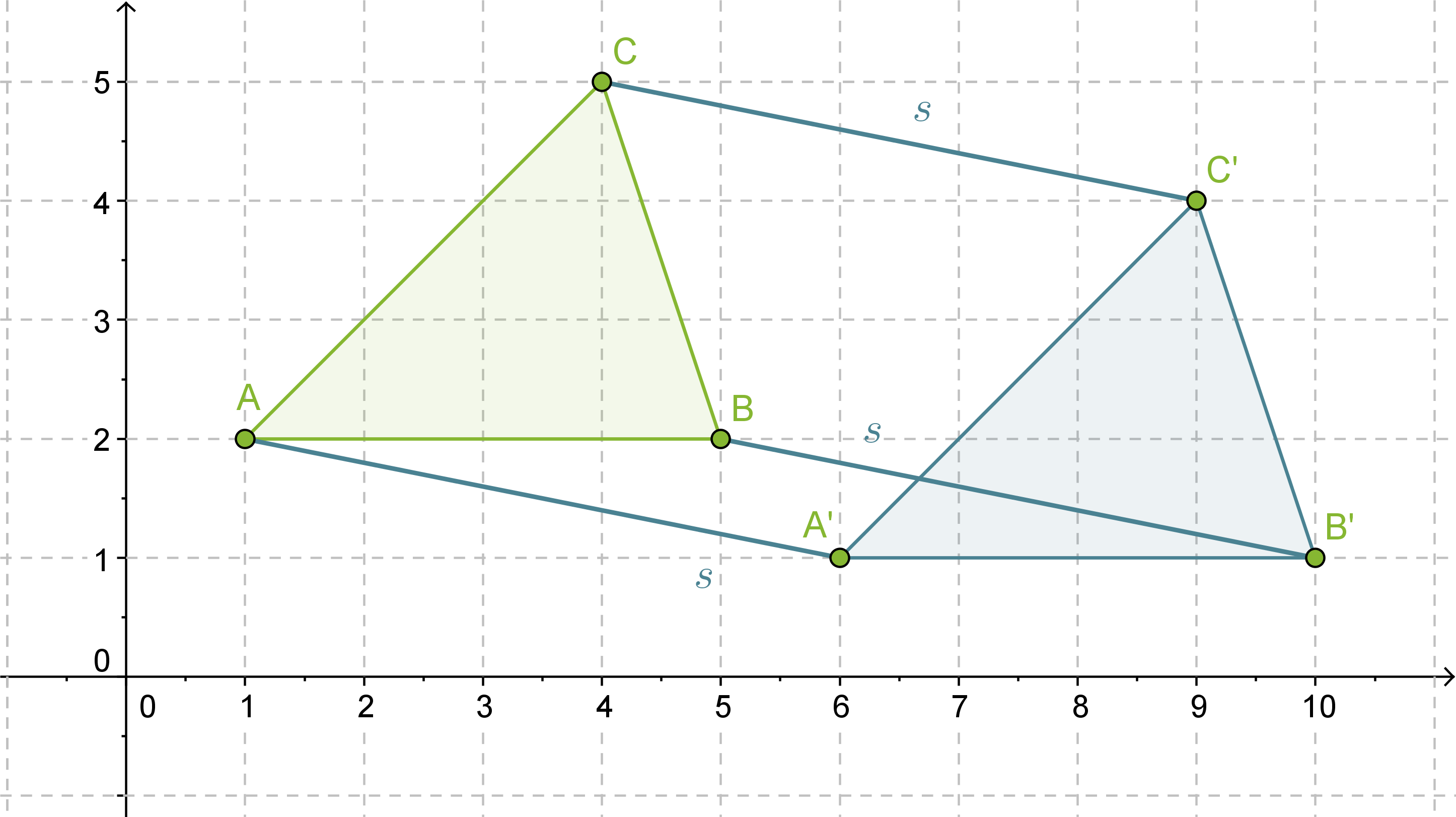
Siirretään kolmiota ABC suuntajanan s = ”1 yksikkö alas ja 5 yksikköä oikealle” verran.
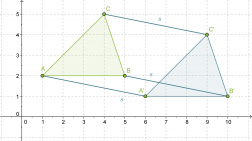
Klikkaa kuva suuremmaksi!
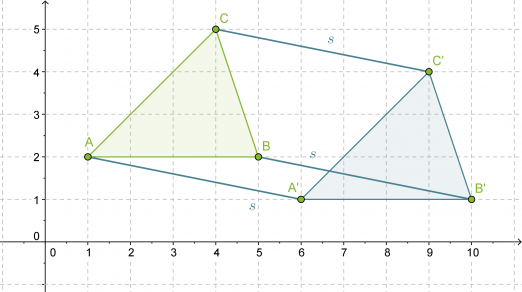
Klikkaa kuva suuremmaksi!
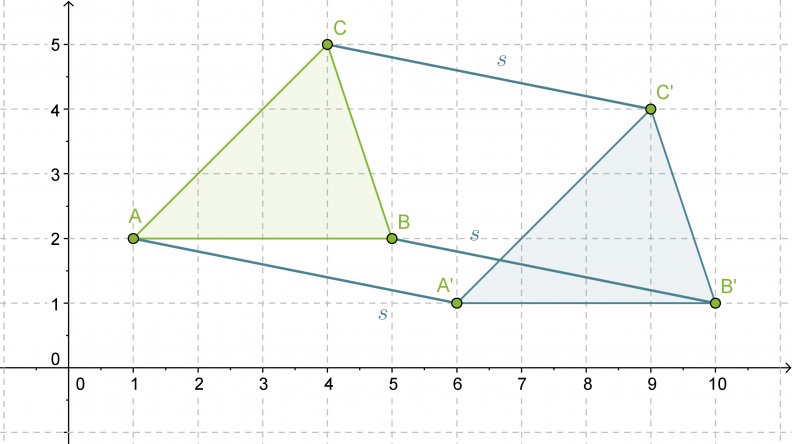
Klikkaa kuva suuremmaksi!
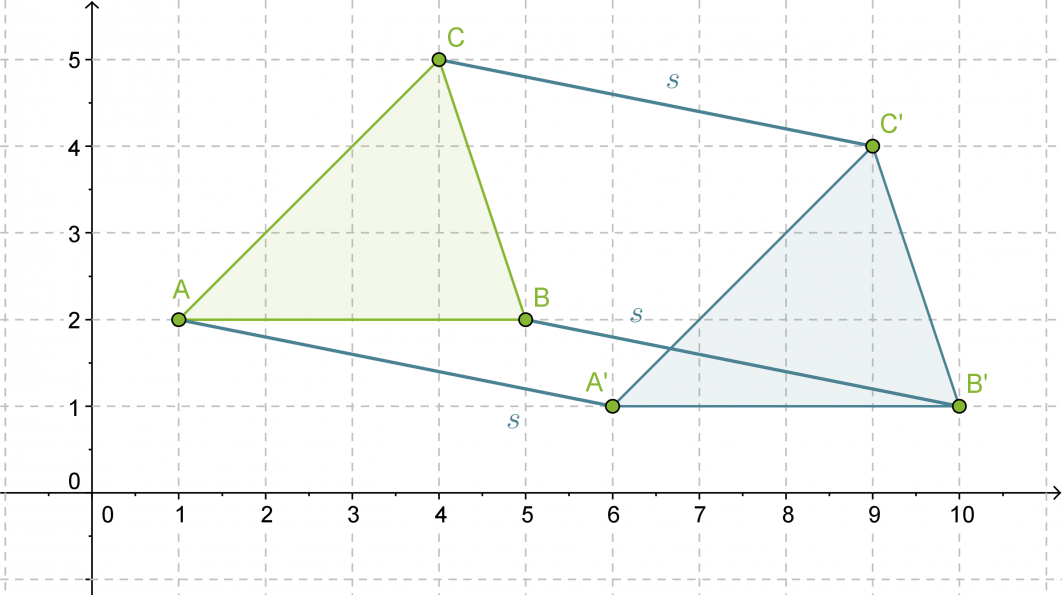
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kierto
Kierrossa kuvion jokaista pistettä kierretään kulman α verran kiertokeskuksen O ympäri siten, että kunkin pisteen etäisyys pisteeseen O säilyy.
Kierron suhteen symmetrinen kuvio kuvautuu kulman α suuruisessa kierrossa itselleen, tällöin sanotaan, että kuvio on symmetrinen kulman α suuruisen kierron suhteen.
Esimerkki 2.
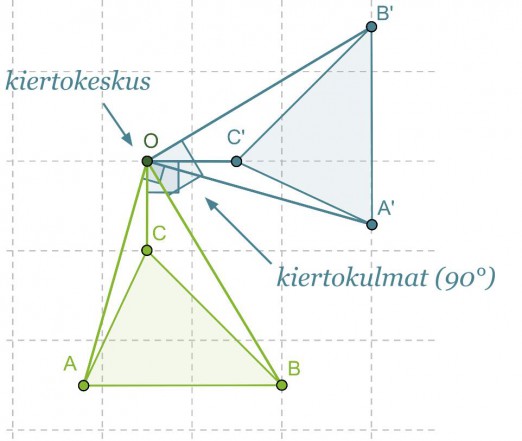
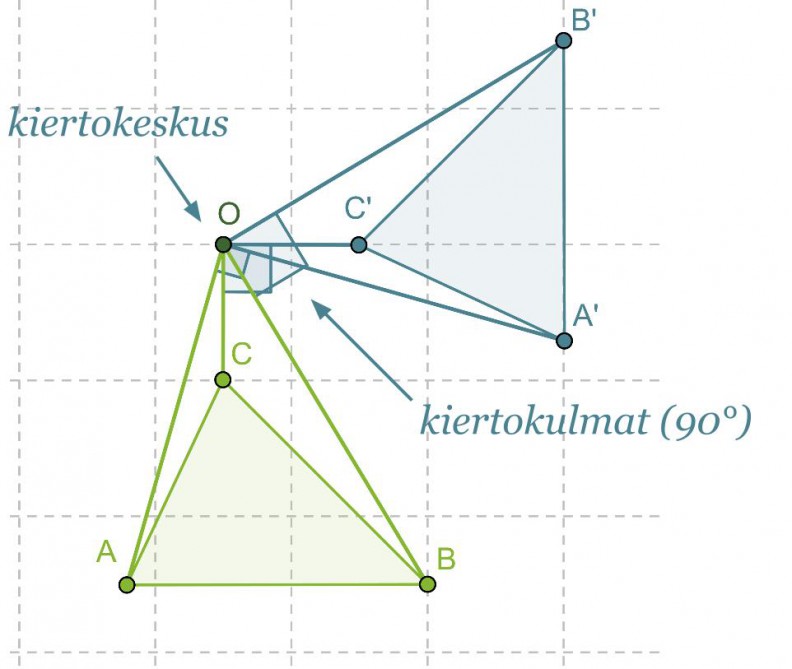
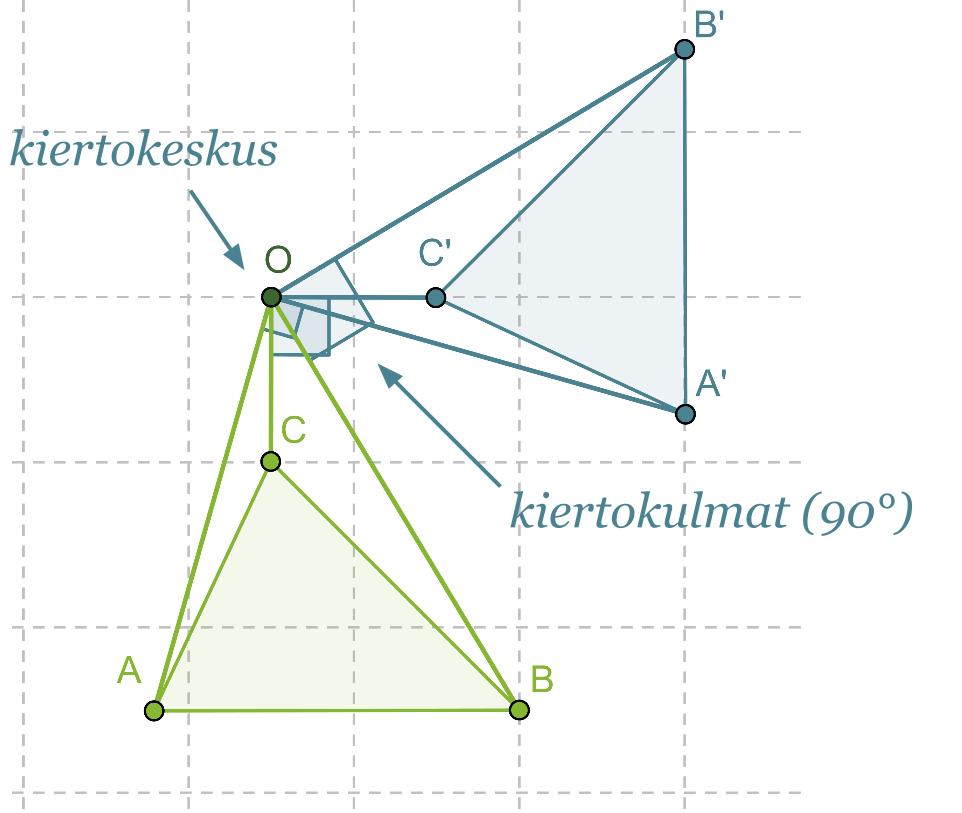
Kierrettään kolmiota ABC pisteen O ympäri 90 asteen verran vastapäivään.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 3.
Jos viereistä kuviota kierretään keskipisteensä ympäri 180°, näyttää se täsmälleen samalta alkuperäisen kuvion kanssa ja sijaitsee täsmälleen samassa paikassa. Tällöin sanotaan, että on kiertosymmetrinen kulmalla 180°.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Koska 180° kierto keskipisteen suhteen voidaan tehdä kahdesti ennen kuin saavutetaan täysi kierros, on keskipiste symmetrisen kuvauksen kaksinkertainen kiertokeskus.
Avoin matematiikka 8Osio 3: Tasogeometriaa5.6.2014
Yhdensuuntaissiirto
Yhdensuuntaissiirrossa kuvion kaikkia pisteitä siirretään yhtä pitkä matka samaan suuntaan.