8. Neliöjuuri
Esimerkki 1.
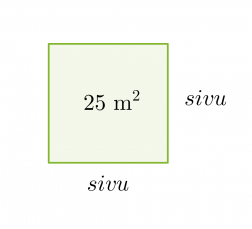
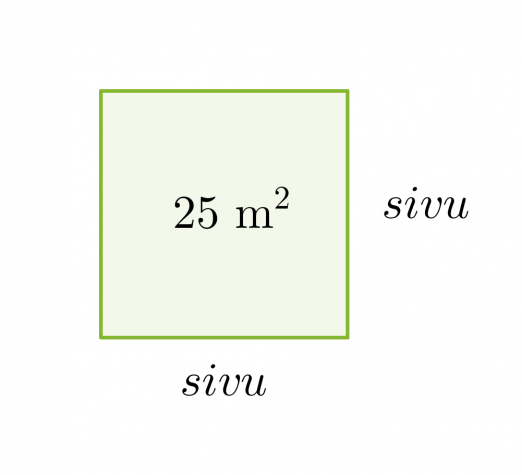
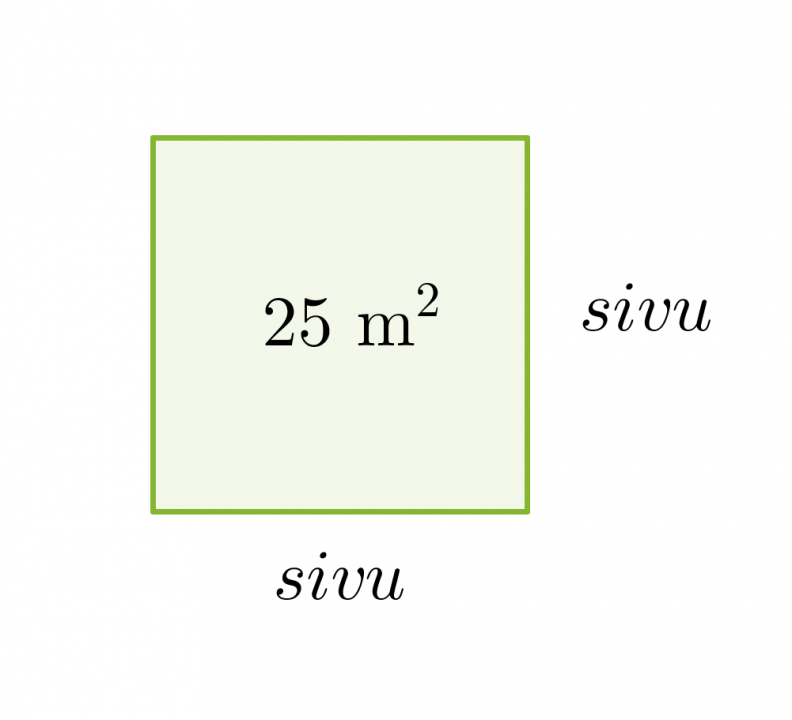
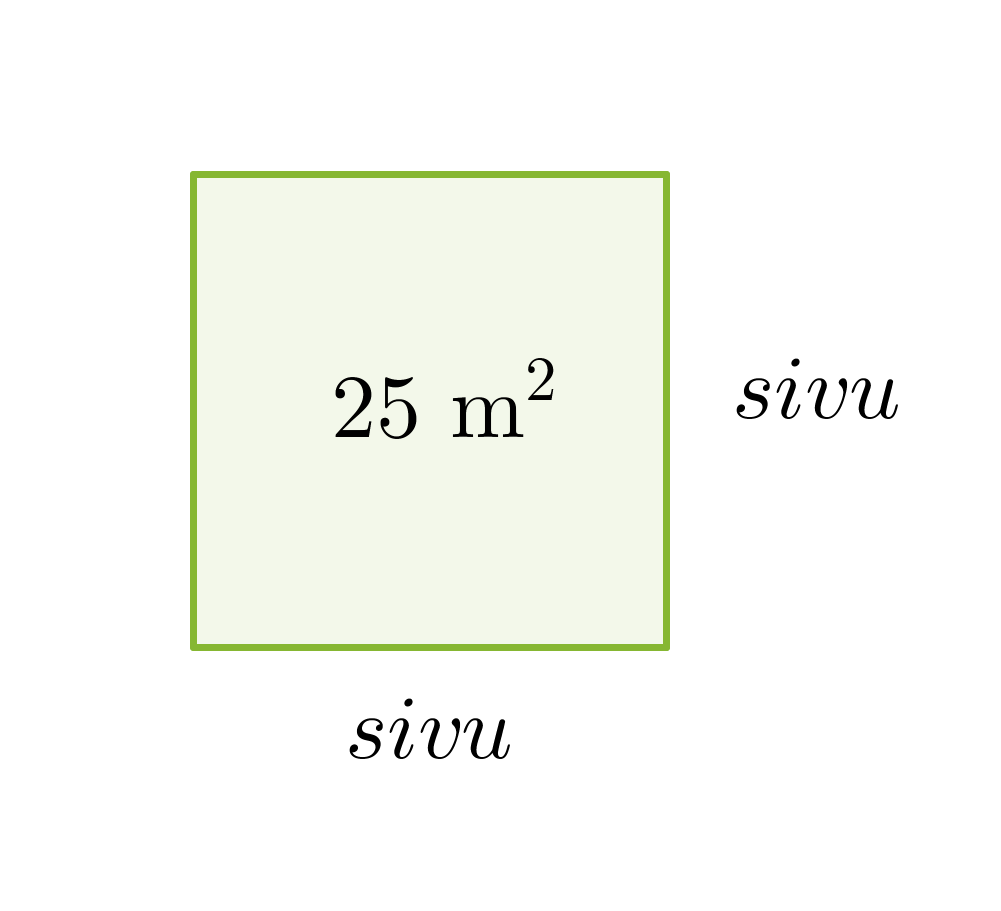
Lasketaan neliön muotoisen lattian yhden sivun pituus, kun lattian pinta-ala on 25 m2.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
Neliön pinta-ala on 25 m2, jolloin yhden sivun pituuden täytyy olla 5 m, koska 5 m · 5 m = 25 m2.
Entä jos neliön muotoisen lattian pinta-ala onkin 20 m2? Mikä on tällöin yhden sivun pituus?
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
Jos sivun pituus olisi 4 m, lattian pinta-ala olisi 4 m · 4 m = 16 m2. Sivun pituus ei ole nyt kokonaisluku, vaan se täytyy olla jotakin 4 m ja 5 m väliltä. Tehtävän voisi ratkaista kokeilemalla, mutta ratkaisu löytyy helpommin, kun otetaan laskimella neliöjuuri luvusta 20.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tarkistus: (4,47 m)2 = 19,9809 m2 ≈ 20 m2.
Neliöön korottamisen käänteinen toiminto on neliöjuuren ottaminen. Neliöjuuri vastaa siis kysymykseen, ”Mikä luku on korotettava toiseen potenssiin, jotta saadaan kyseessä oleva luku?”.
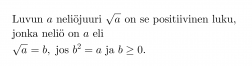
Klikkaa kuva suuremmaksi!
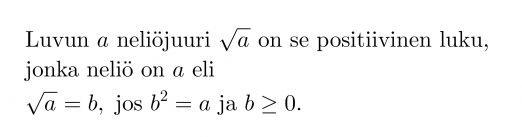
Klikkaa kuva suuremmaksi!
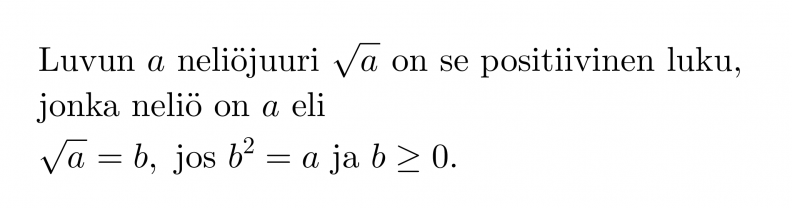
Klikkaa kuva suuremmaksi!
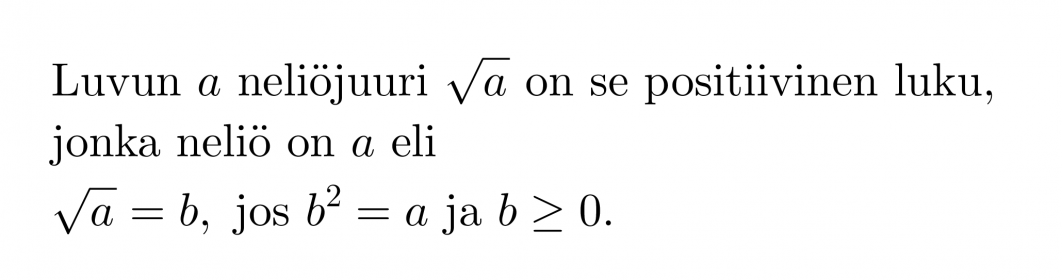
Klikkaa kuva suuremmaksi!
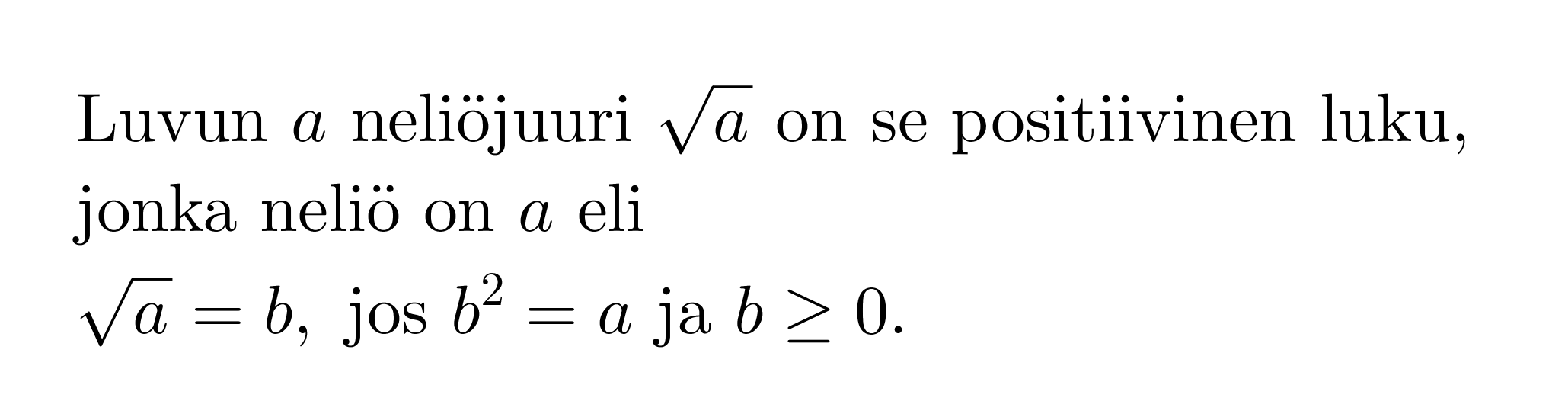
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.

Klikkaa kuva suuremmaksi!
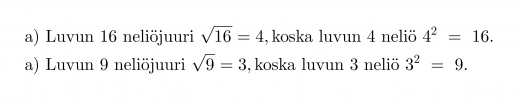
Klikkaa kuva suuremmaksi!
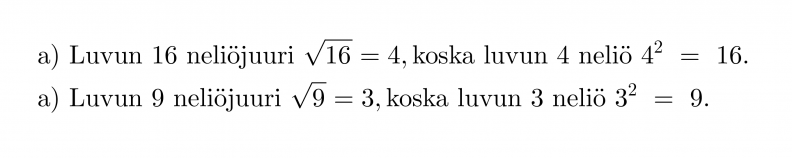
Klikkaa kuva suuremmaksi!
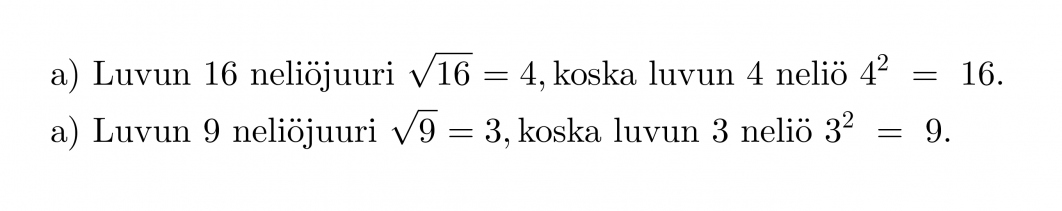
Klikkaa kuva suuremmaksi!
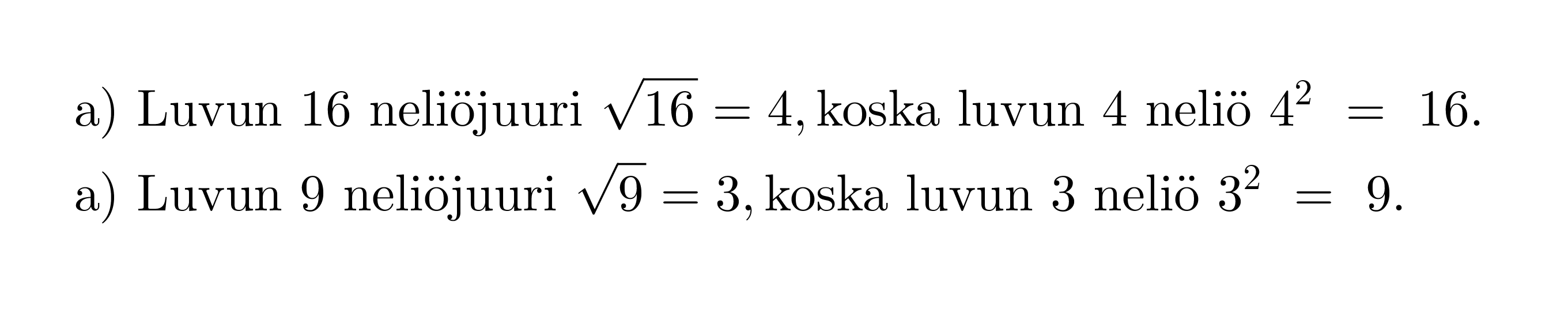
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 3.
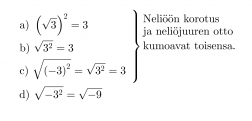
Klikkaa kuva suuremmaksi!
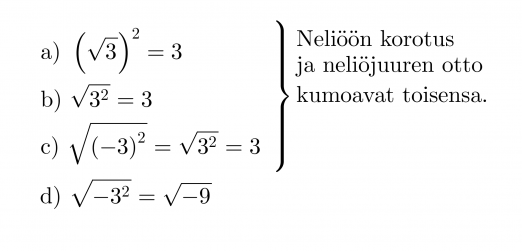
Klikkaa kuva suuremmaksi!
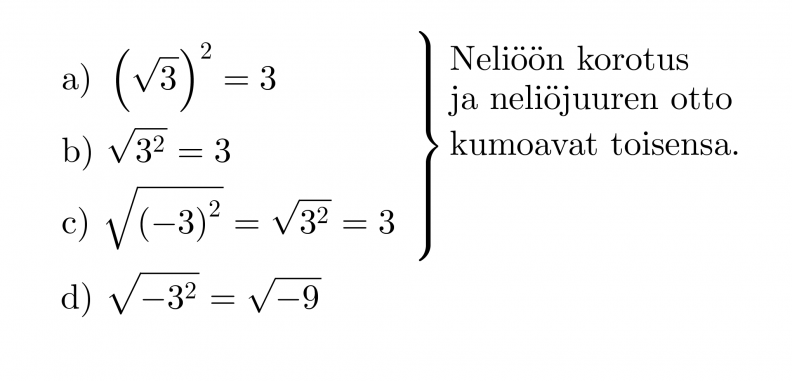
Klikkaa kuva suuremmaksi!
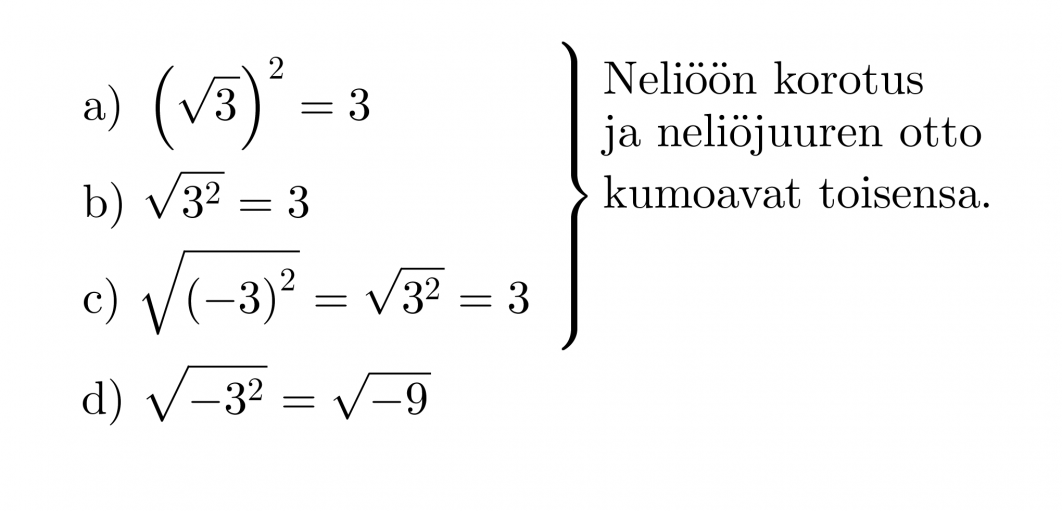
Klikkaa kuva suuremmaksi!
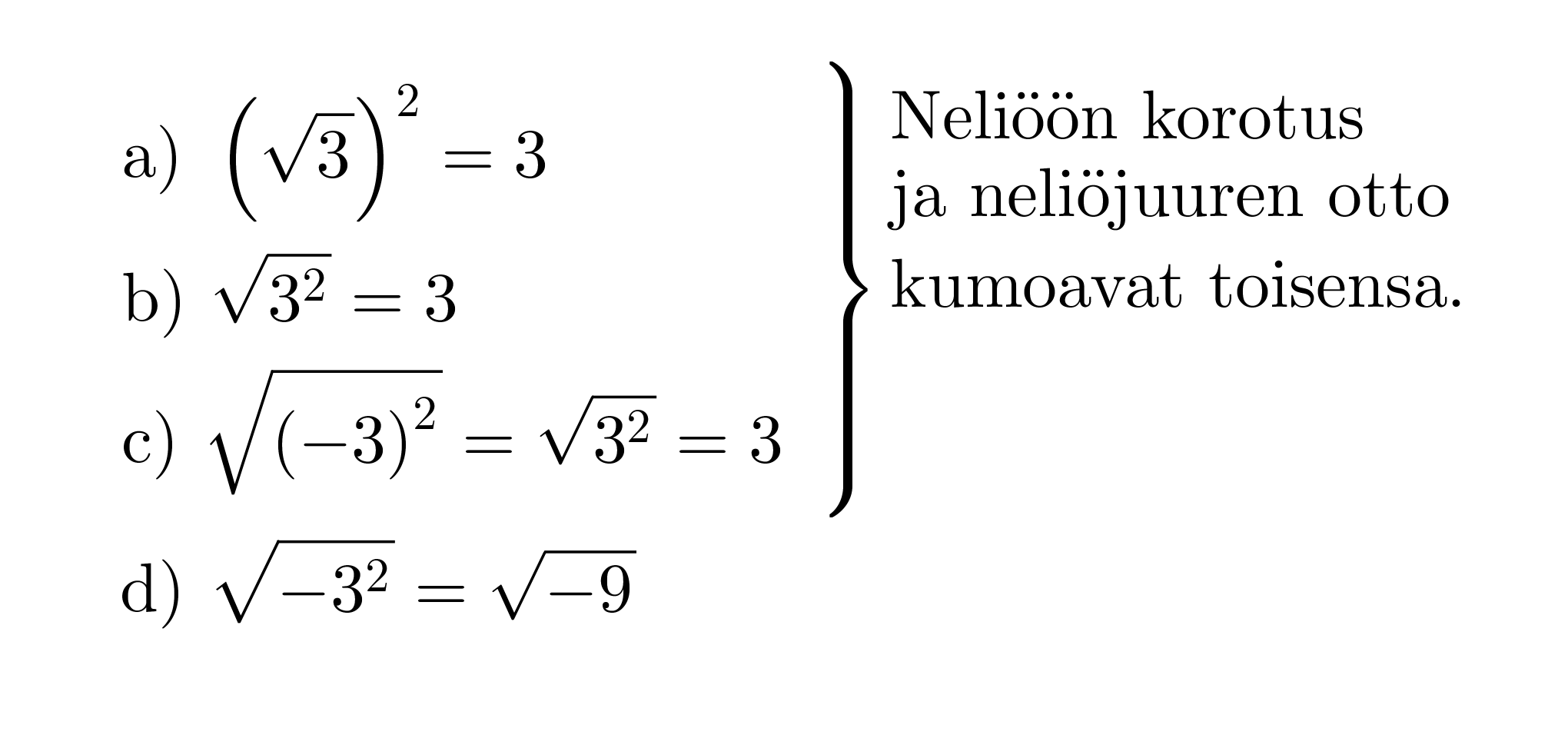
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
d) Ei ole määritelty, koska potenssin kantalukuna on pelkkä 3 ja negatiivisesta luvusta ei voi ottaa neliöjuurta.
“Neliöjuurta ei voi ottaa negatiivisesta luvusta, eikä neliöjuuren arvo ole koskaan negatiivinen.”