10. Pythagoraan lause
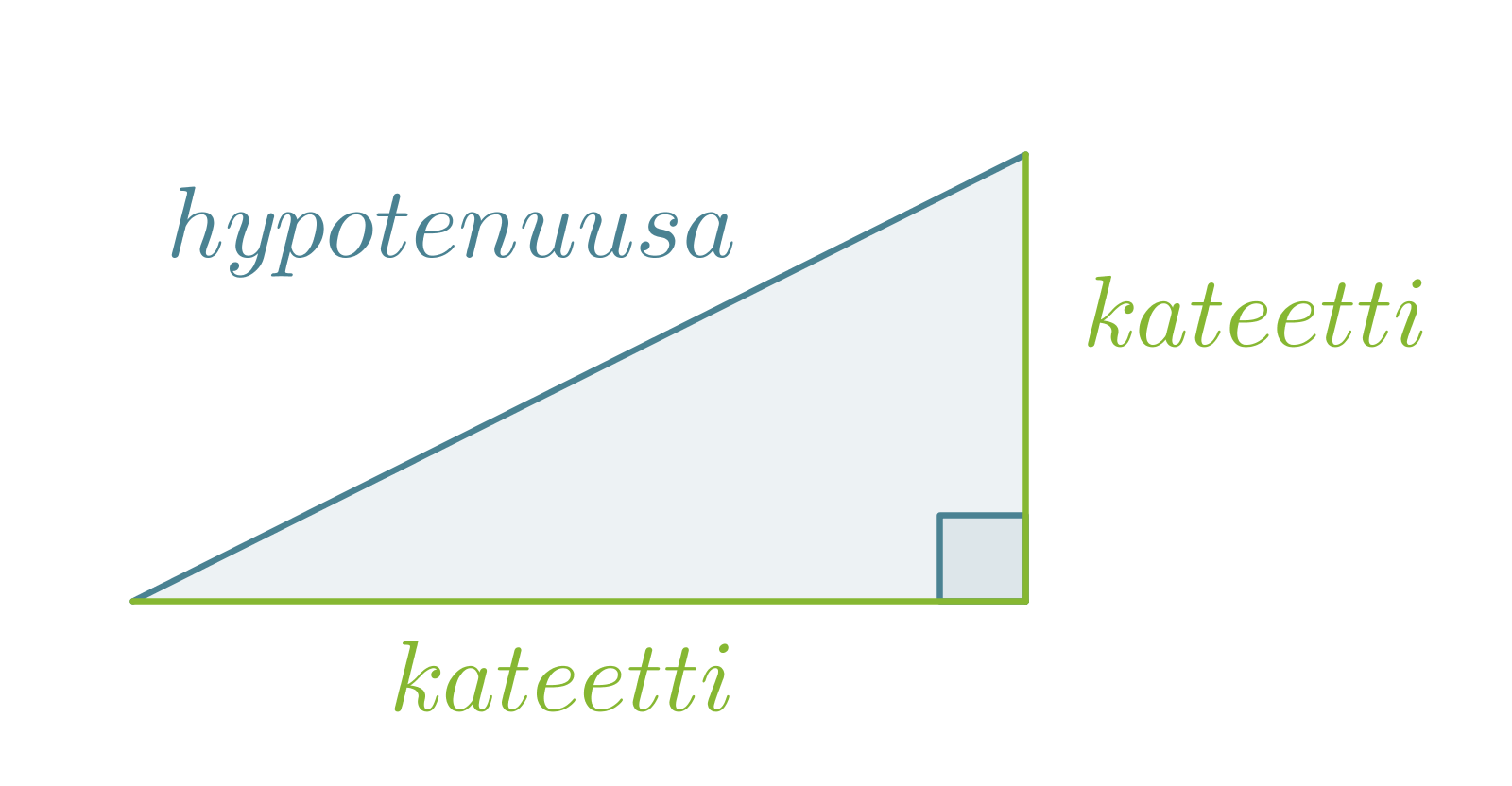
Hypotenuusa on suorakulmaisessa kolmiossa suoran kulman vastainen sivu. Suoran kulman viereisiä sivuja sanotaan kateeteiksi.
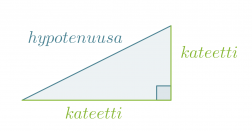
Klikkaa kuva suuremmaksi!
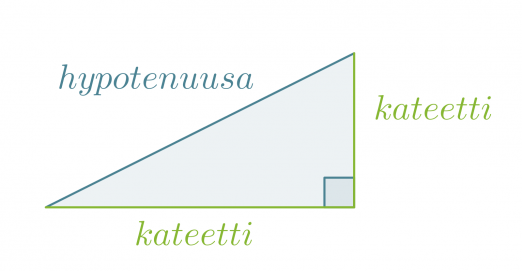
Klikkaa kuva suuremmaksi!
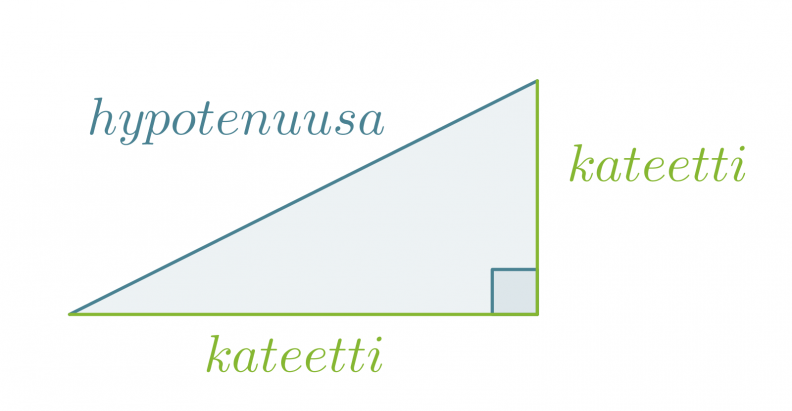
Klikkaa kuva suuremmaksi!
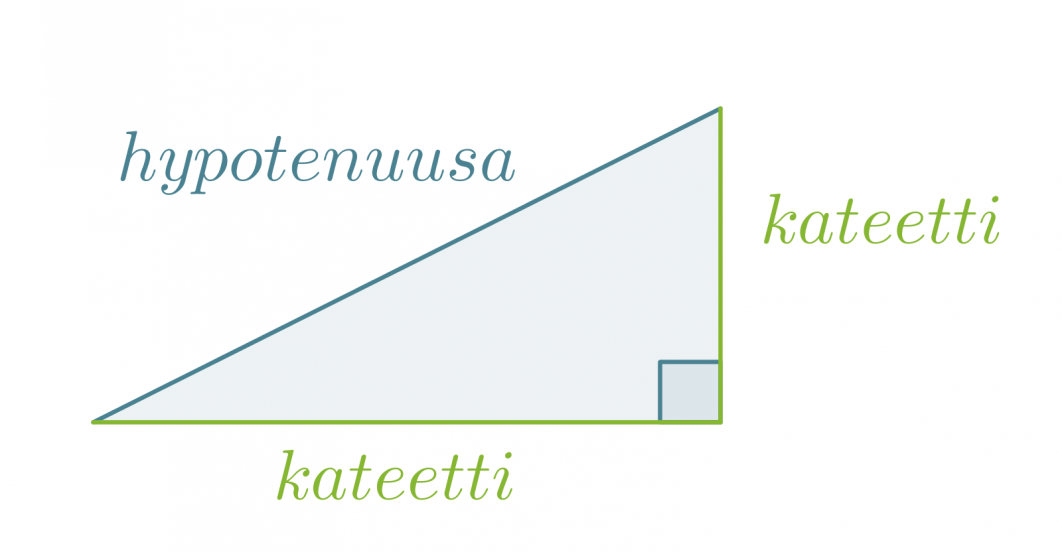
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Hypotenuusa on aina suorakulmaisen kolmion pisin sivu.
Tarkasteellaan suorakulmaista kolmiota, jonka kateettien pituudet ovat 3 ja 4 ja hypotenuusan pituus on 5.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
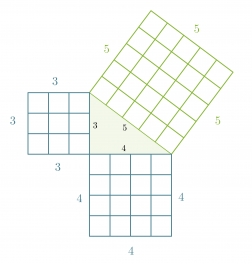
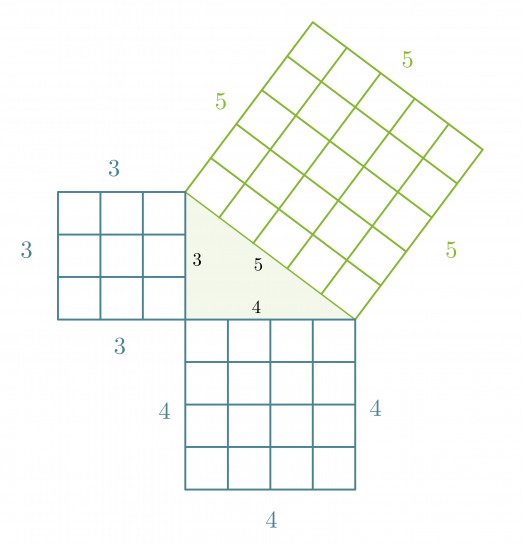
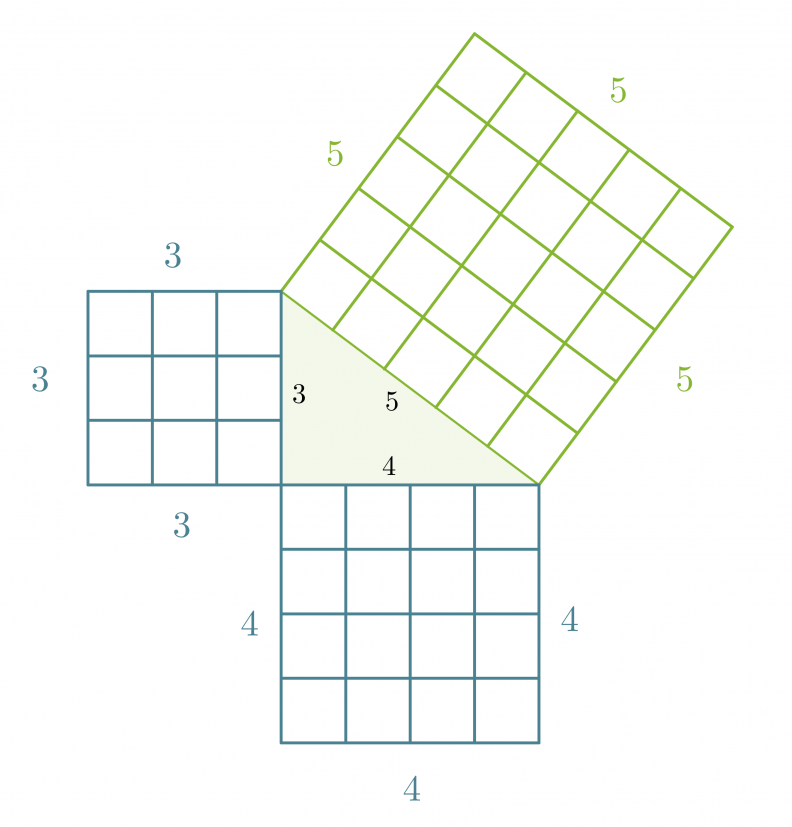
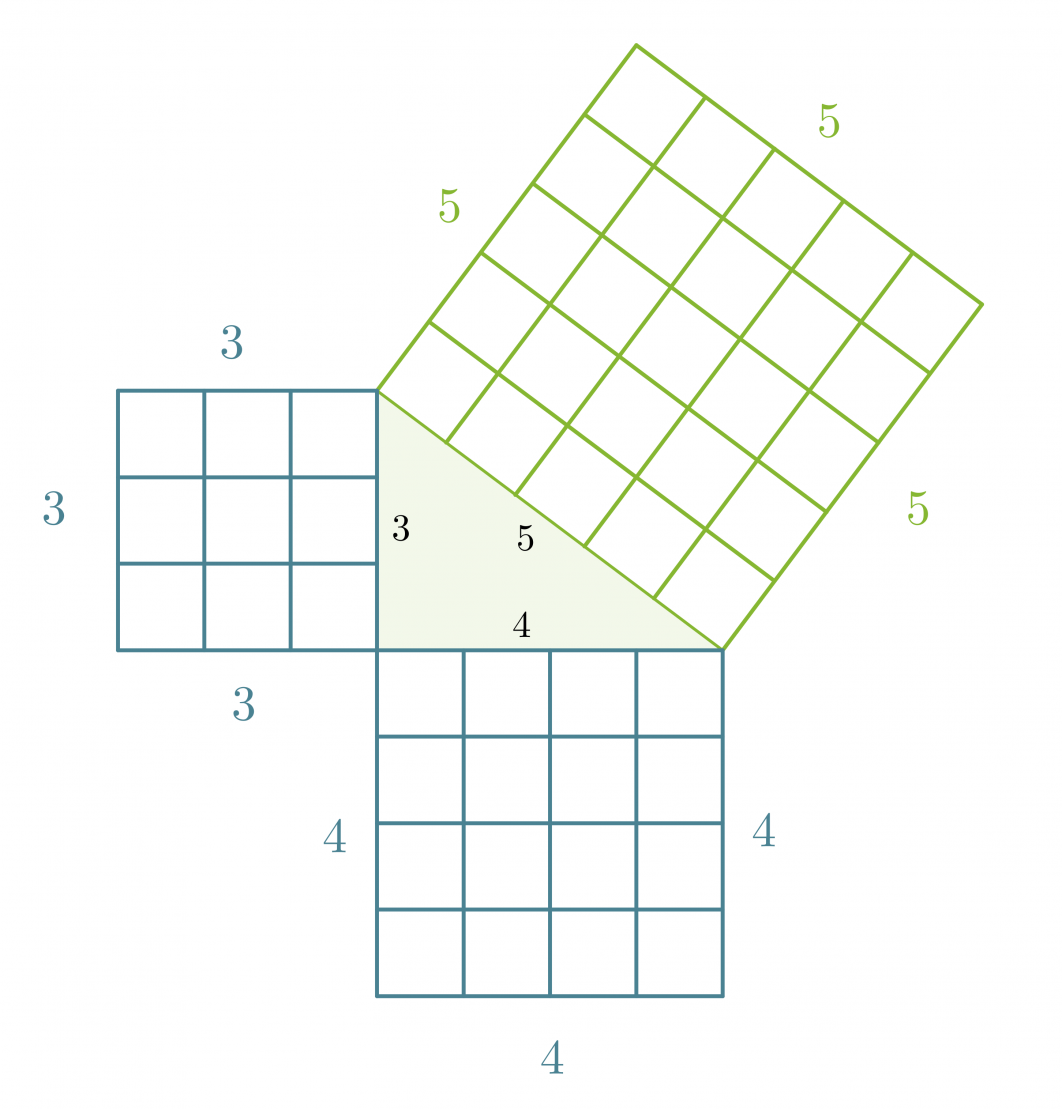
Piirretään kolmion sivuille neliöt, joiden sivujen pituudet ovat yhtä suuret kuin kolmion sivujen pituudet.
Kateettien neliöiden pinta-alat: 32 = 9 ja 42 = 16.
Hypotenuusan neliön pinta-ala: 52 = 25.
Jos kateettien neliöiden pinta-alat lasketaan yhteen: 9 + 16 = 25, saadaan hypotenuusan neliön pinta-ala. Tämä ominaisuus on voimassa kaikissa suorakulmaisissa kolmioissa ja se tunnetaan nimellä Pythagoraan lause.
Pythagoraan lause: Suorakulmaisessa kolmiossa kateettien neliöiden summa on hypotenuusan neliö.
a2+b2=c2
Pythagoraan lauseen avulla voidaan tukia onko kolmio suorakulmainen.
Avoin matematiikka 8Osio 3: Tasogeometriaa5.6.2014
Kolmion suorakulmaisuuden tutkiminen
Jos kolmion kahden lyhyemmän sivun neliöiden summa on yhtä suuri kuin pisimmän sivun neliö, on kolmio suorakulmainen.