11. Pythagoraan lauseen sovelluksia
Pythagoraan lauseen avulla voidaan ratkaista mikä tahansa suorakulmion sivun pituuksista, jos kaksi sen muista sivunpituuksista tunnetaan. Kun Pythagoraan lauseeseen sijoitetaan arvoja, on oltava tarkkana, että sijoittaa kateettien pituudet ja hypotensuusan pituuden oikeaan paikkaan. Tämän jälkeen tuntematon muuttuja ratkeaa normaaleja yhtälönratkaisusääntöjä noudattaen.
Esimerkki 1.
Lasketaan suorakulmaisen kolmion hypotenuusan pituus, kun tiedetään kateettien pituudet.
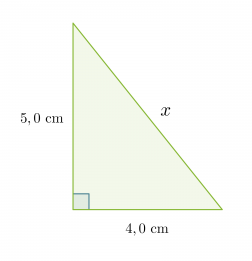
Klikkaa kuva suuremmaksi!
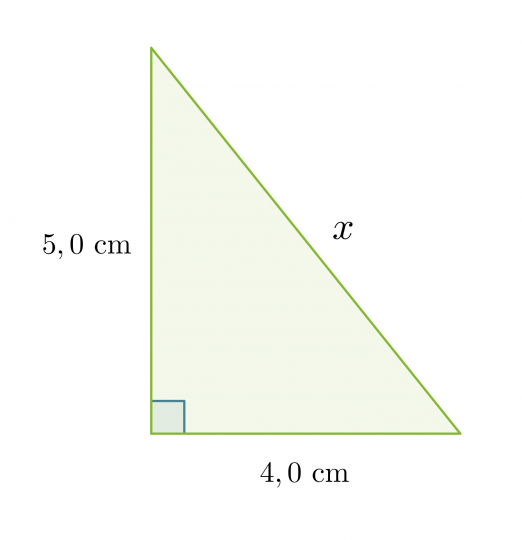
Klikkaa kuva suuremmaksi!
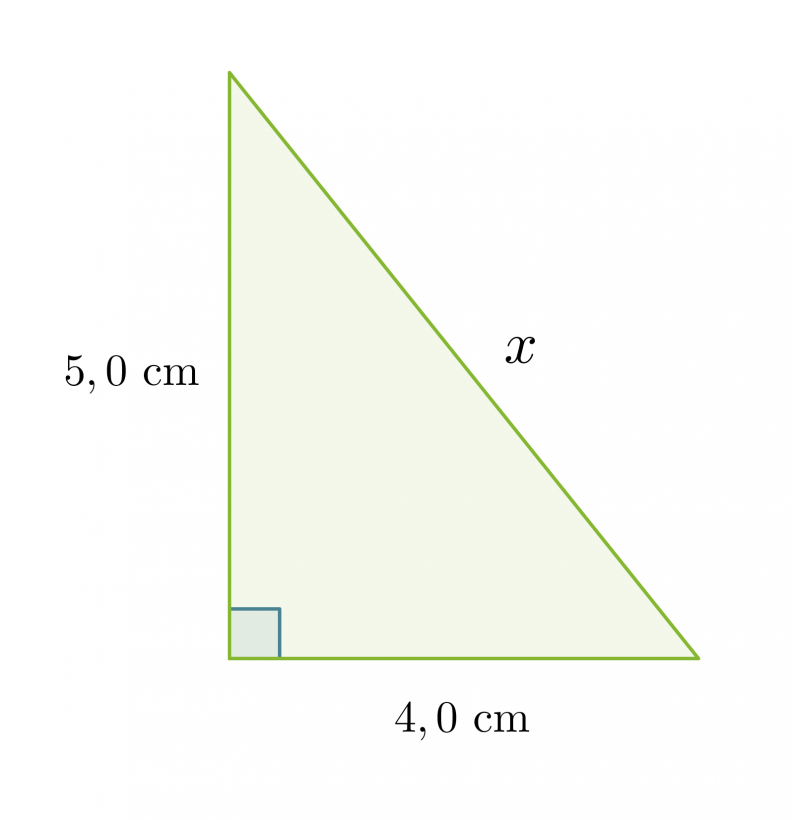
Klikkaa kuva suuremmaksi!
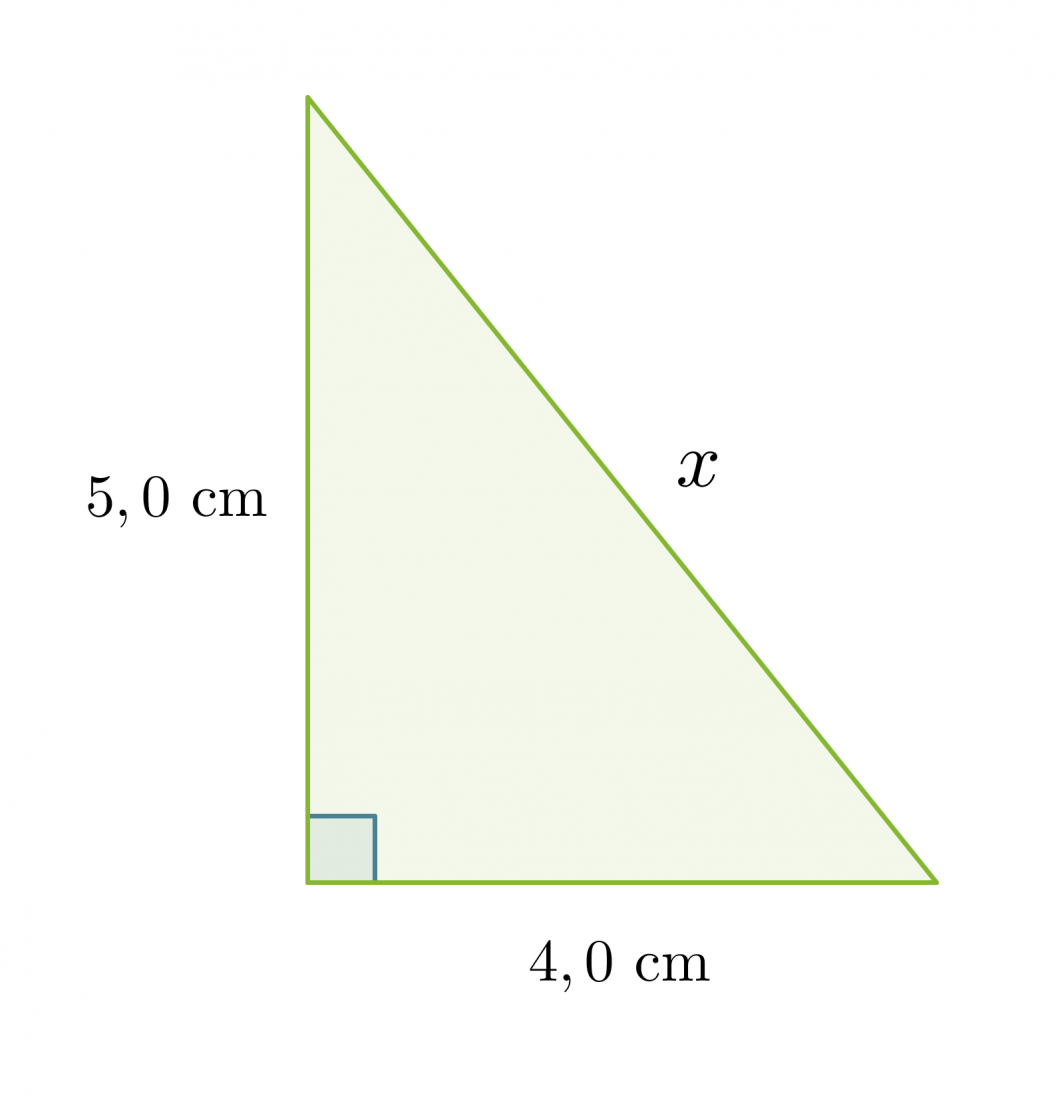
Klikkaa kuva suuremmaksi!
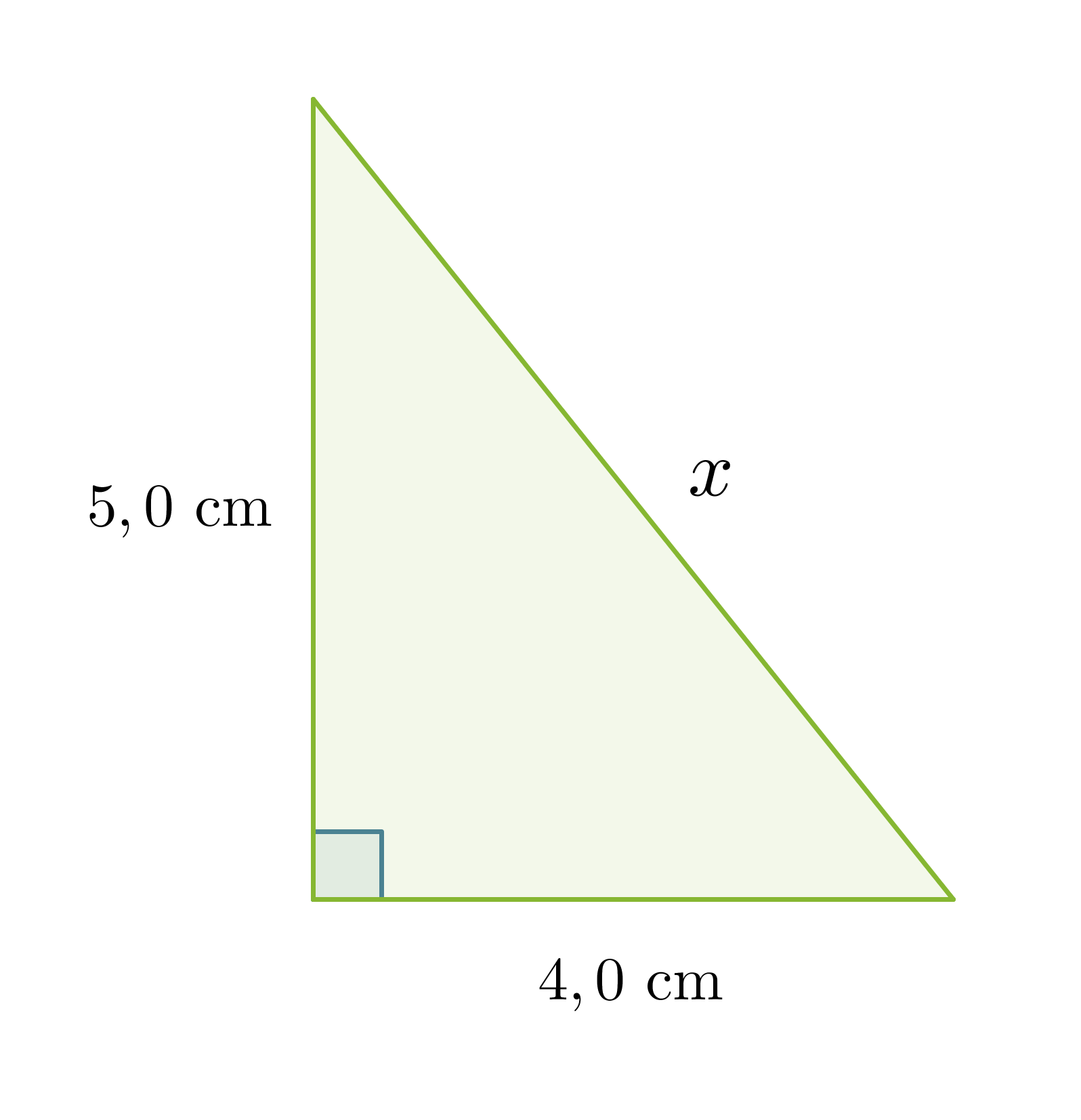
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Sijoitetaan sivujen pituuden Pythagoran lauseeseen.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Hypotenuusan pituus on 6,4 cm.
Esimerkki 2.
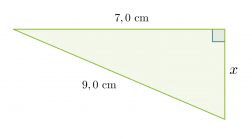
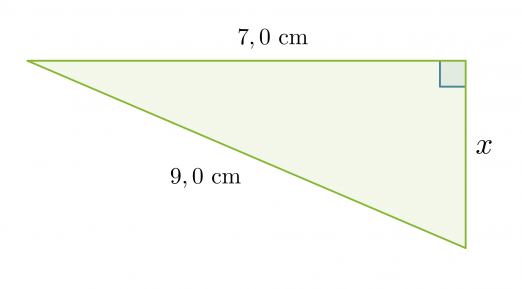
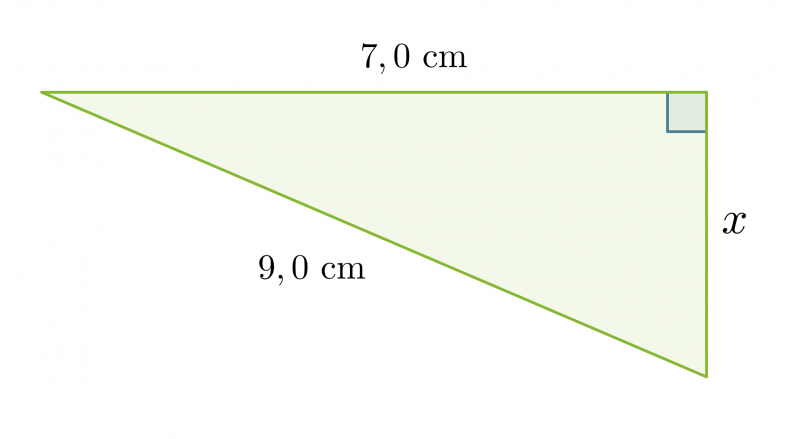
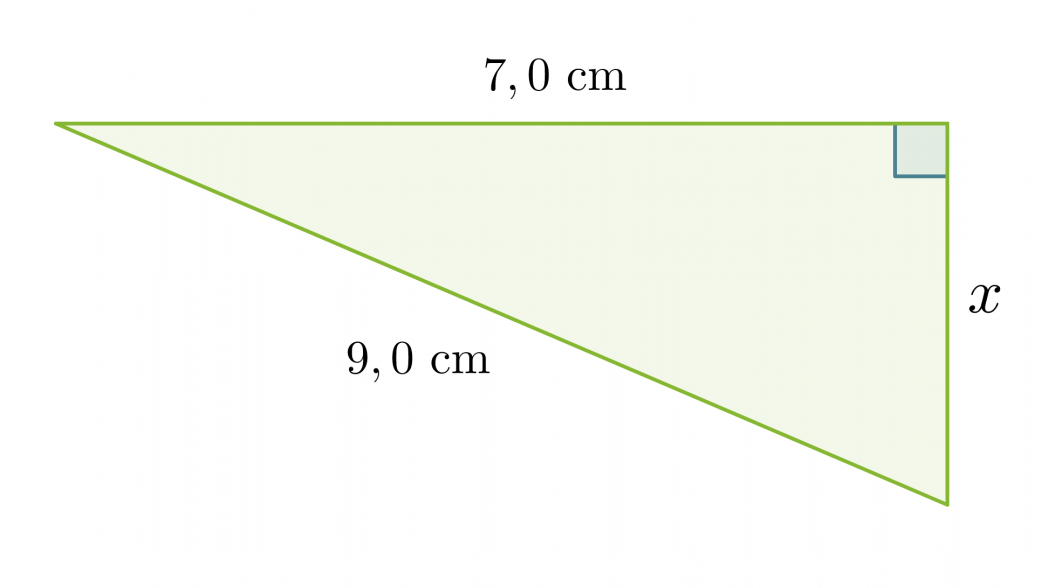
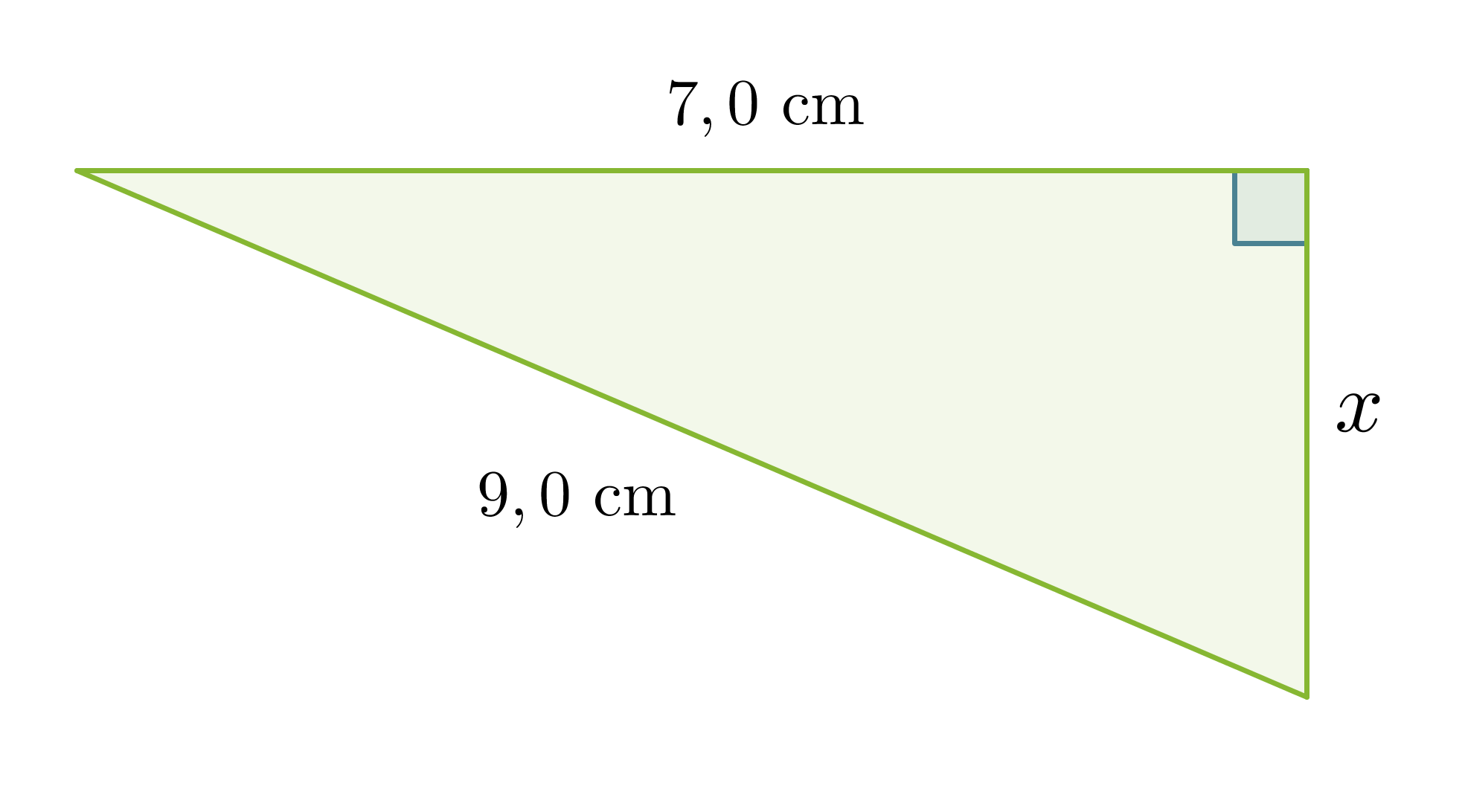
Lasketaan viereisen suorakulmaisen kolmion sivun x pituus.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Koska kolmio on suorakulmainen, voidaan soveltaa Pythagoraan lausetta. Kysytty sivu on kateetti ja toinen kateeteista on 7,0 cm. Hypotenuusan pituus on 9,0 cm.
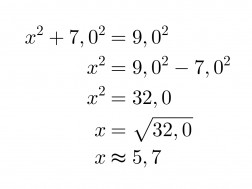
Klikkaa kuva suuremmaksi!
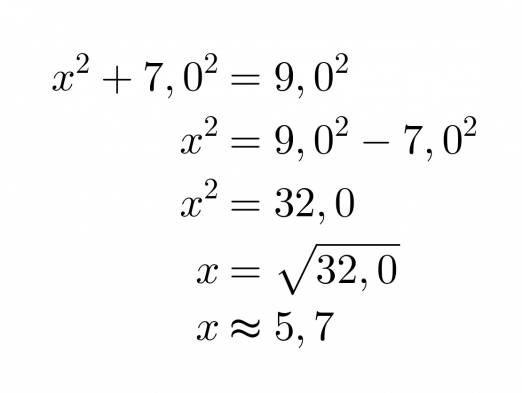
Klikkaa kuva suuremmaksi!
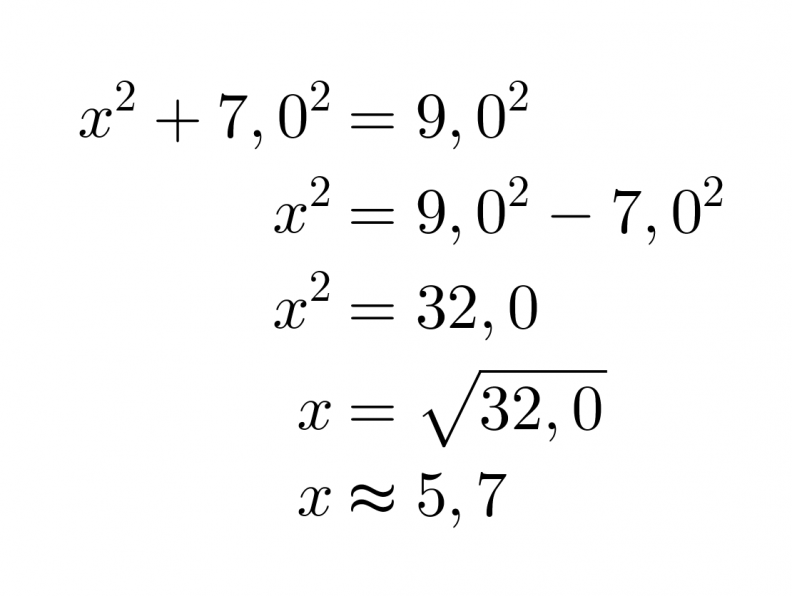
Klikkaa kuva suuremmaksi!
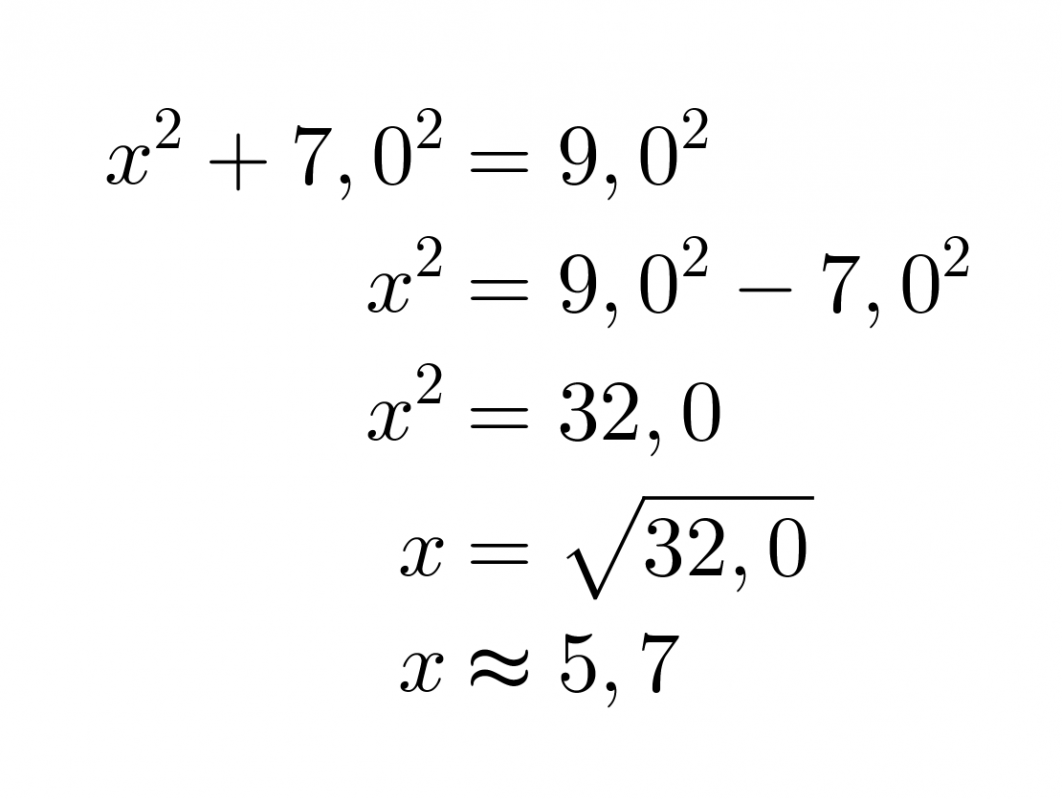
Klikkaa kuva suuremmaksi!
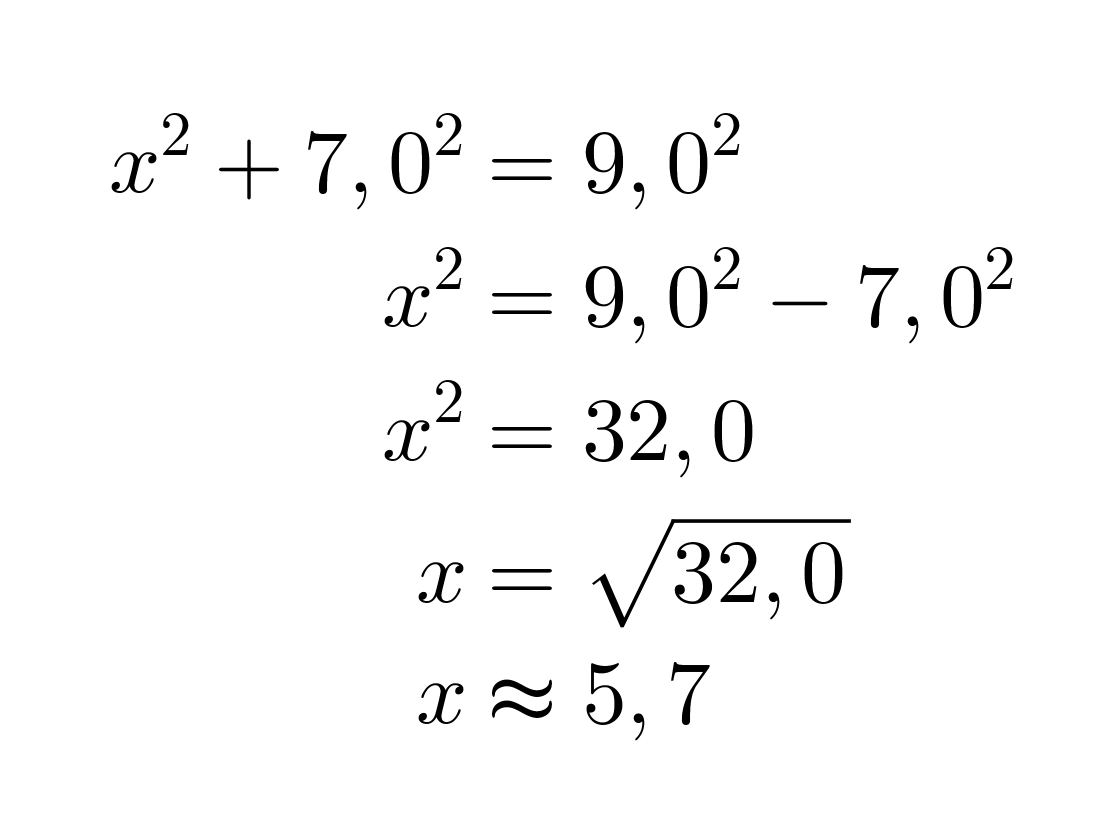
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Sivun x pituus on 5,7 cm.
Esimerkki 3.
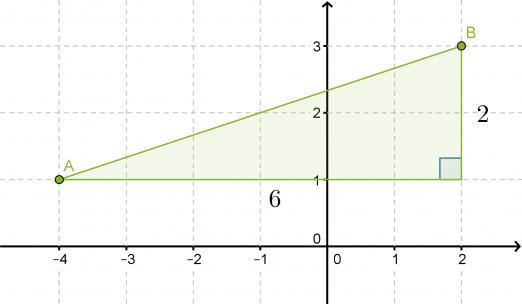
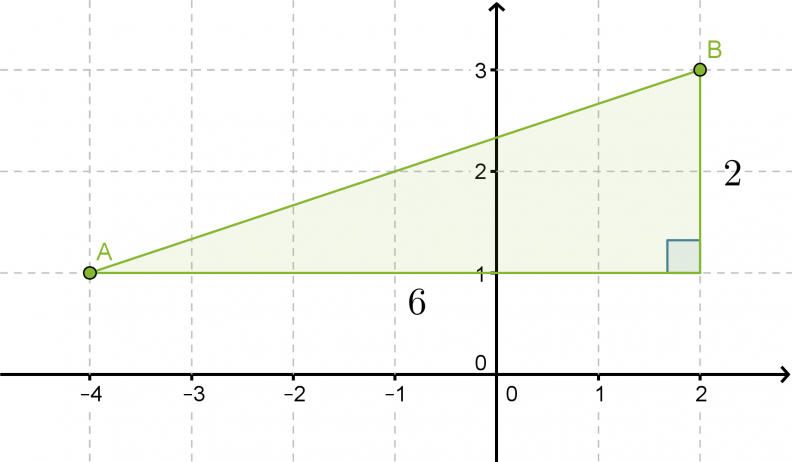
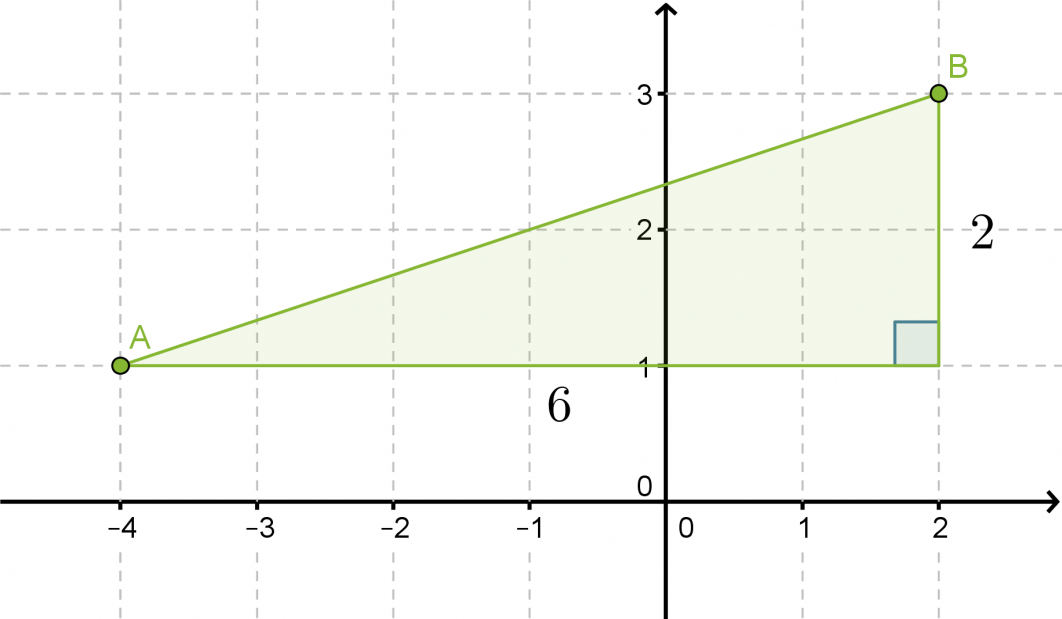
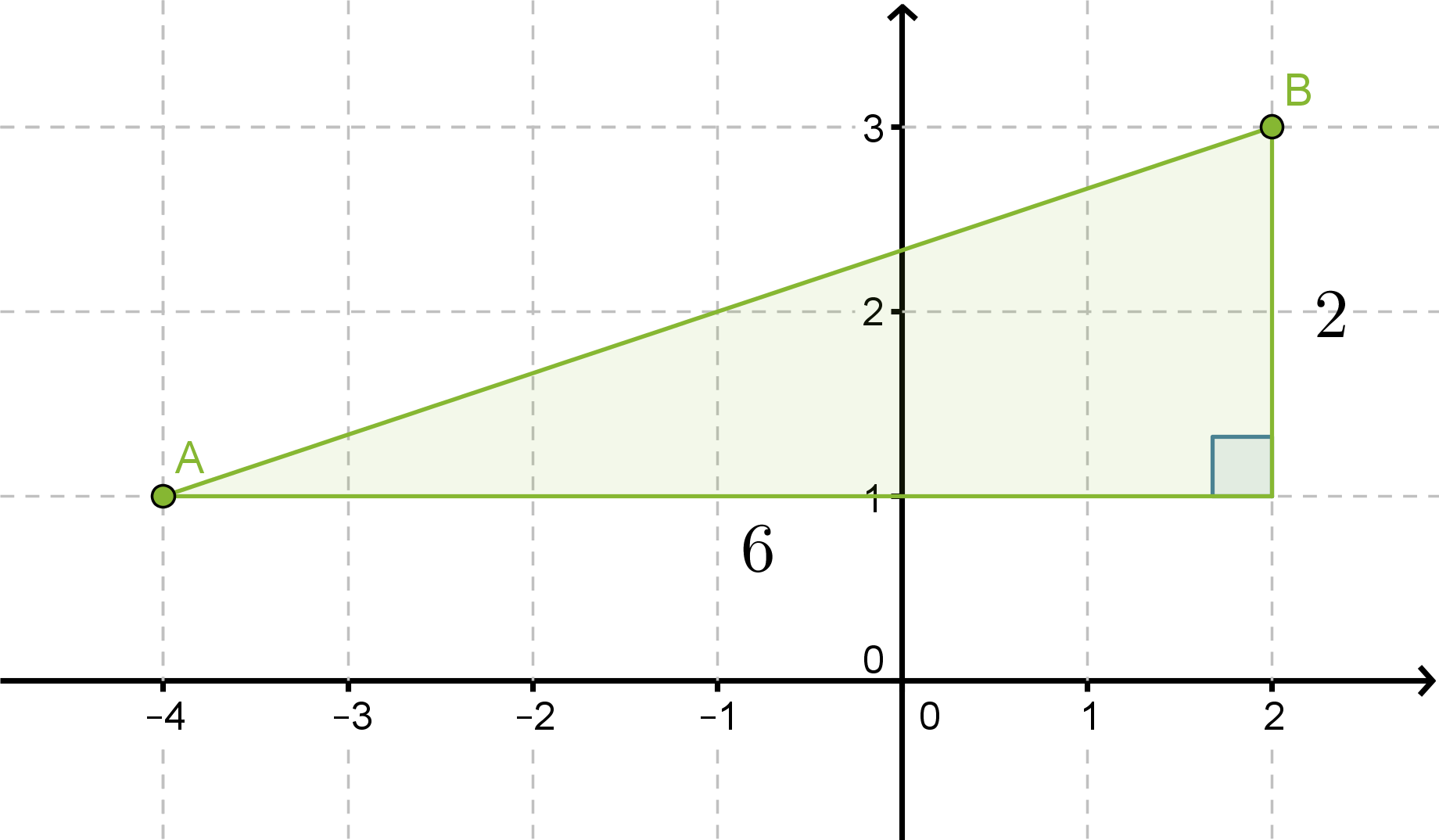
Pisteen A koordinaatit ovat (-4, 1) ja pisteen B (2,3). Laske kuinka kaukana pisteet ovat toisistaan.
Ratkaisu:
Sijoitetaan pisteet A ja B koordinaatistoon ja yhdistetään ne janalla. Täydennetään kuvio suorakulmaiseksi kolmioksi.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Pisteiden etäisyys on suorakulmaisen kolmion hypotenuusan pituus, joten se voidaan laskea käyttämällä Pythagoraan lausetta.
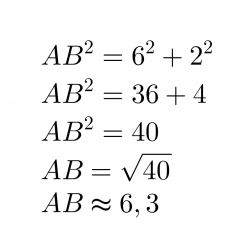
Klikkaa kuva suuremmaksi!
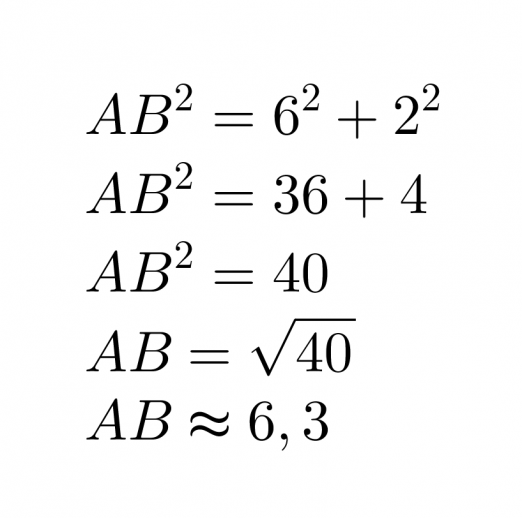
Klikkaa kuva suuremmaksi!
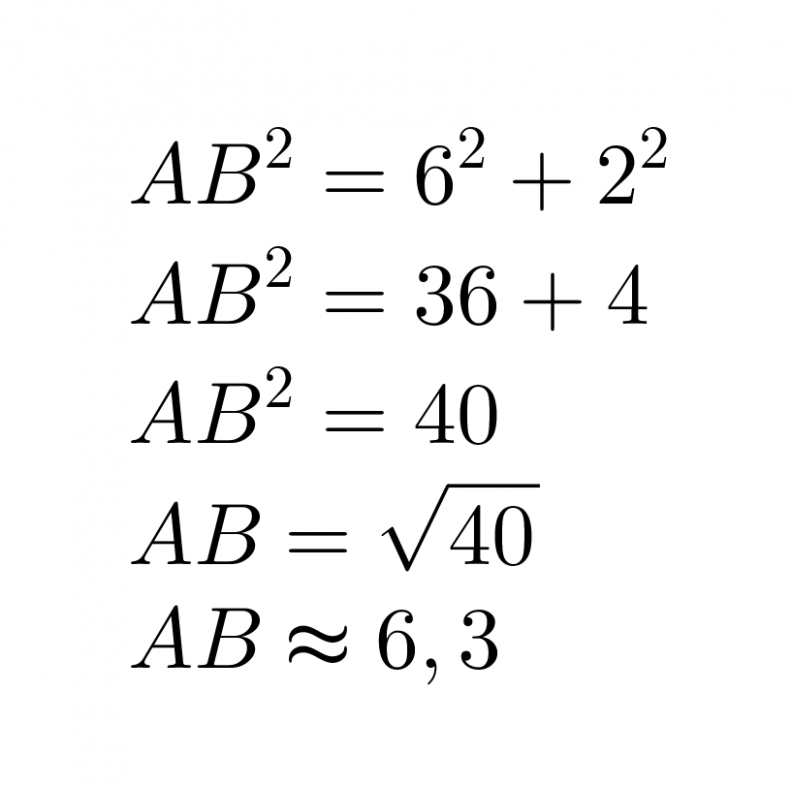
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Pisteiden A ja B välinen etäisyys on 6,3.
Avoin matematiikka 8Osio 3: Tasogeometriaa5.6.2014