14. Ympyrän tangenttikulma

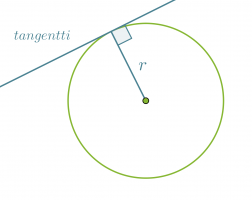
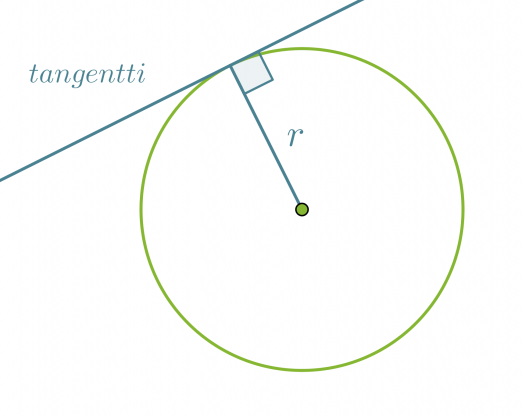
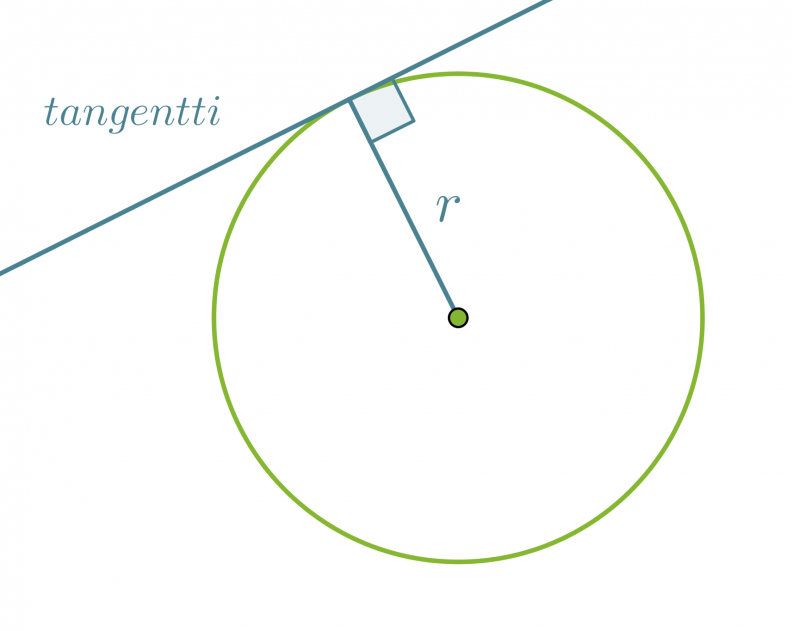
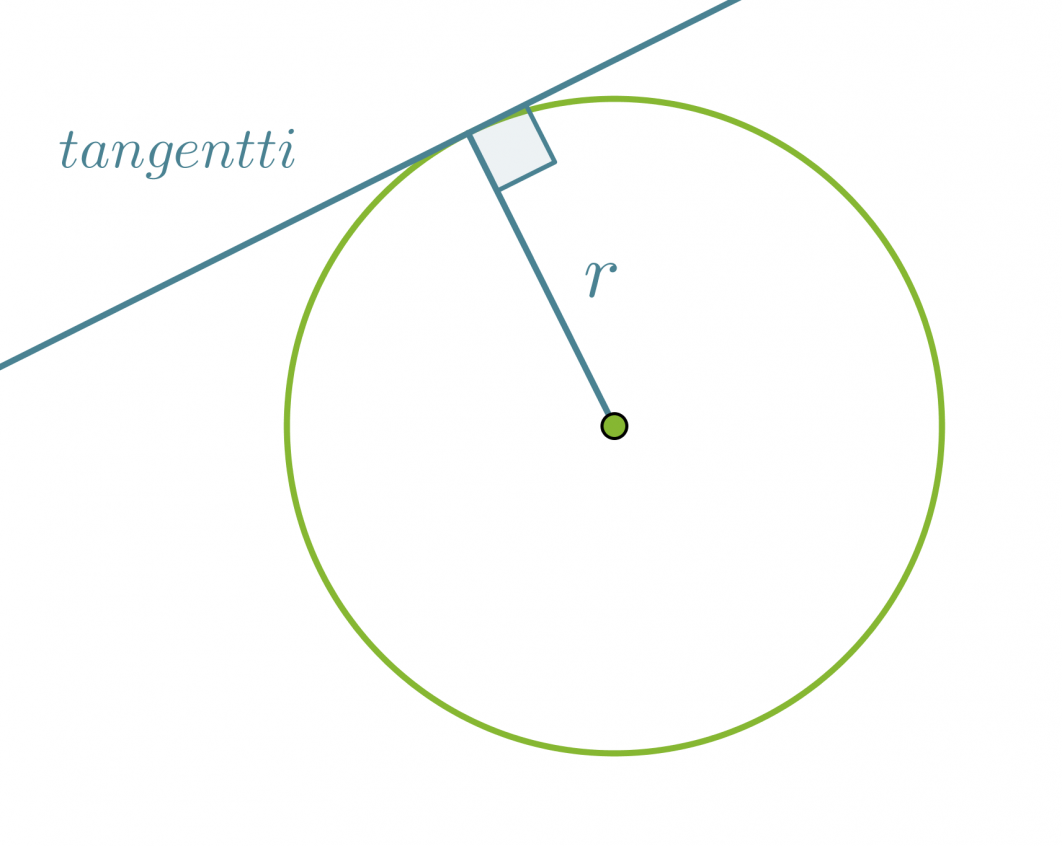
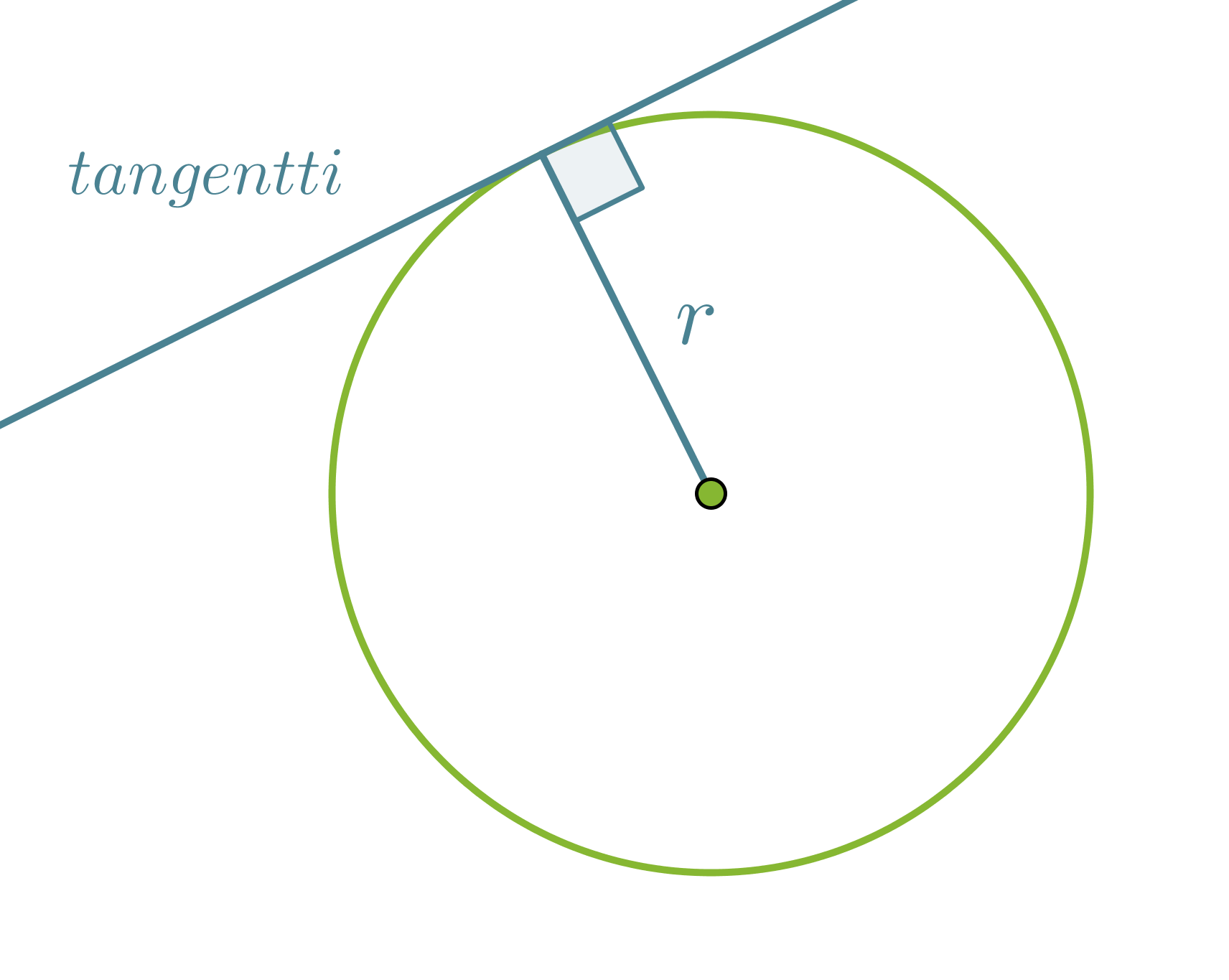
Ym­py­rän tan­gent­ti on suo­ra, joka kul­kee sä­teen ke­häl­lä ole­van pää­te­pis­teen kaut­ta ja on koh­ti­suo­ras­sa sä­det­tä vas­taan. Tan­gent­ti siis si­vu­aa ym­py­rää ai­no­as­taan yh­des­sä pis­tees­sä ja sen etäi­syys ym­py­rän kes­ki­pis­tees­tä on sä­teen suu­rui­nen.

Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

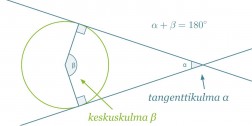
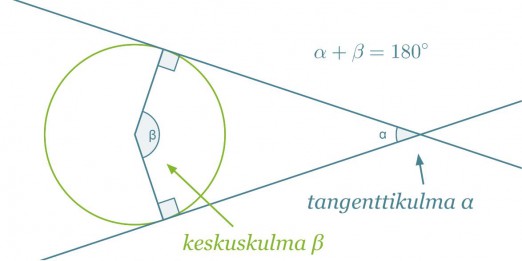
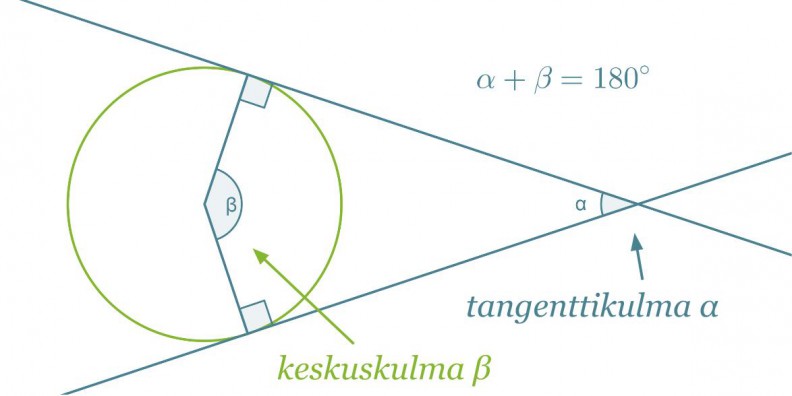
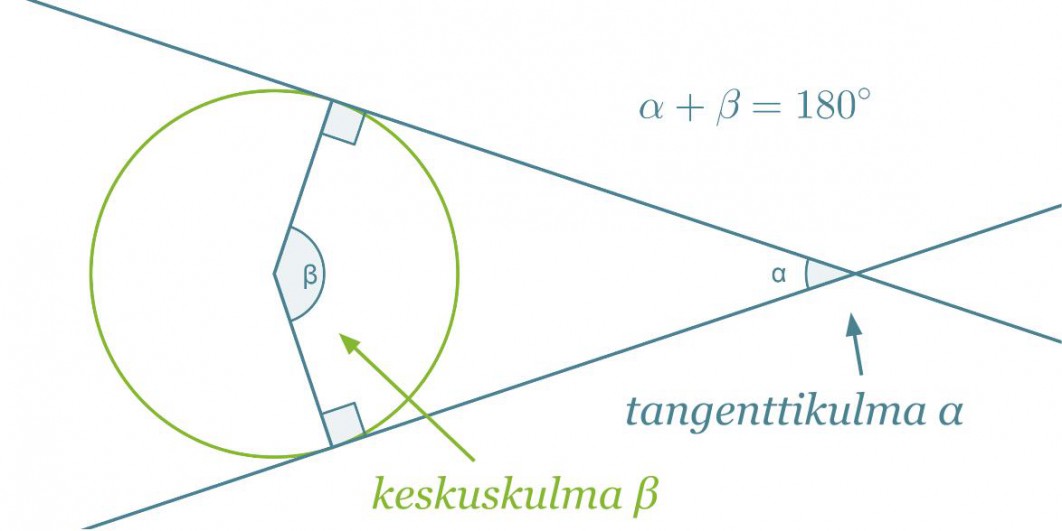
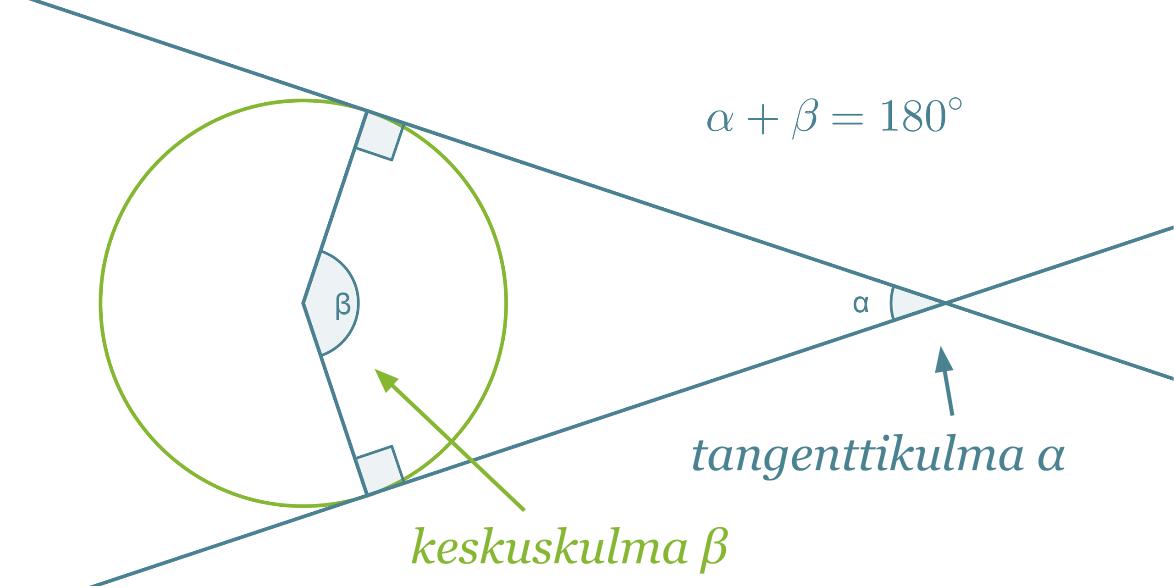
Ym­py­rän ulko­puo­li­sen pis­teen kaut­ta voi­daan ym­py­räl­le piir­tää kak­si tan­gent­tia. Kul­maa, jon­ka kyl­jet si­jait­se­vat ym­py­rän tan­gen­teil­la, sa­no­taan tan­gent­ti­kul­mak­si. Tanganttikulman kyl­jet kär­jes­tä si­vu­a­mis­pis­tei­siin ovat yhtä pit­kät.

Esimerkki 1.

Las­ke­taan kes­kus­kul­man suu­ruus, kun sitä vas­taa­van tan­gent­ti­kul­man suu­ruus on 40^o.

Tan­gent­ti­kul­man ja sitä vas­taa­van kes­kus­kul­man sum­ma on 180°, jo­ten kes­kus­kul­ma on 180° – 40° = 140°.

Esimerkki 2.

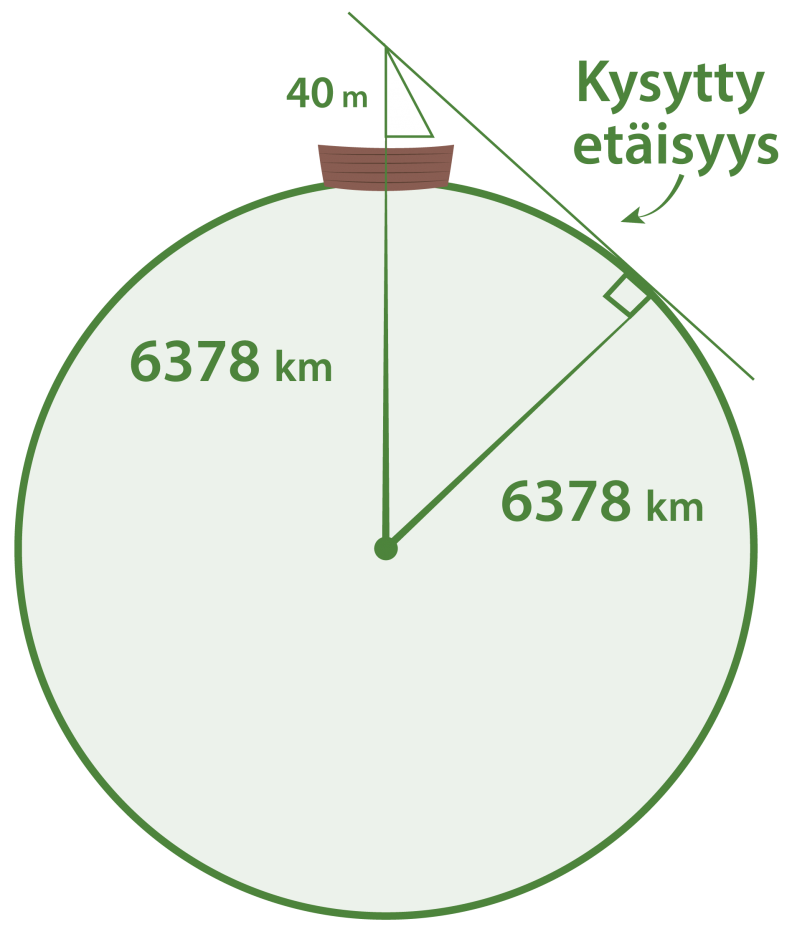
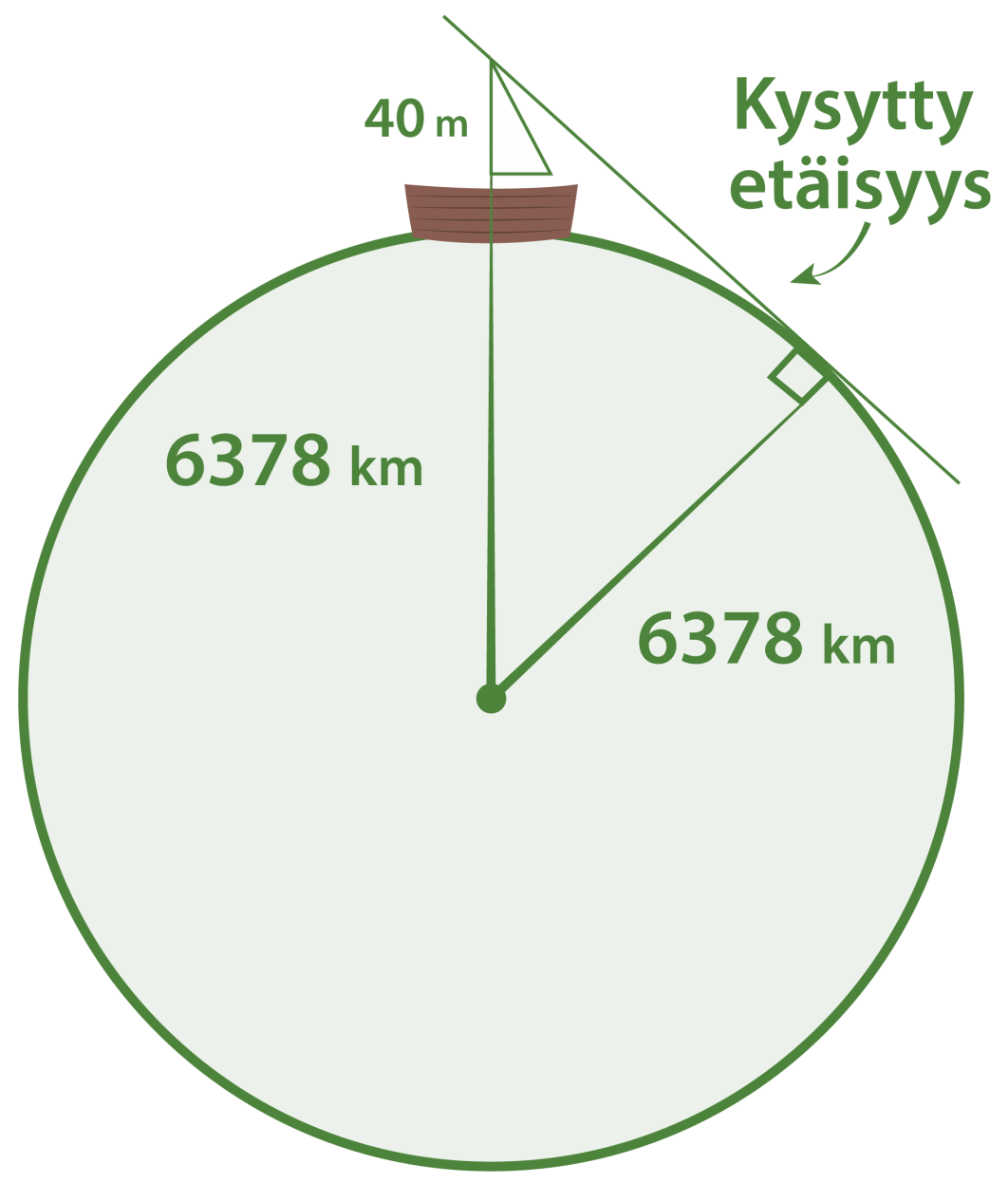
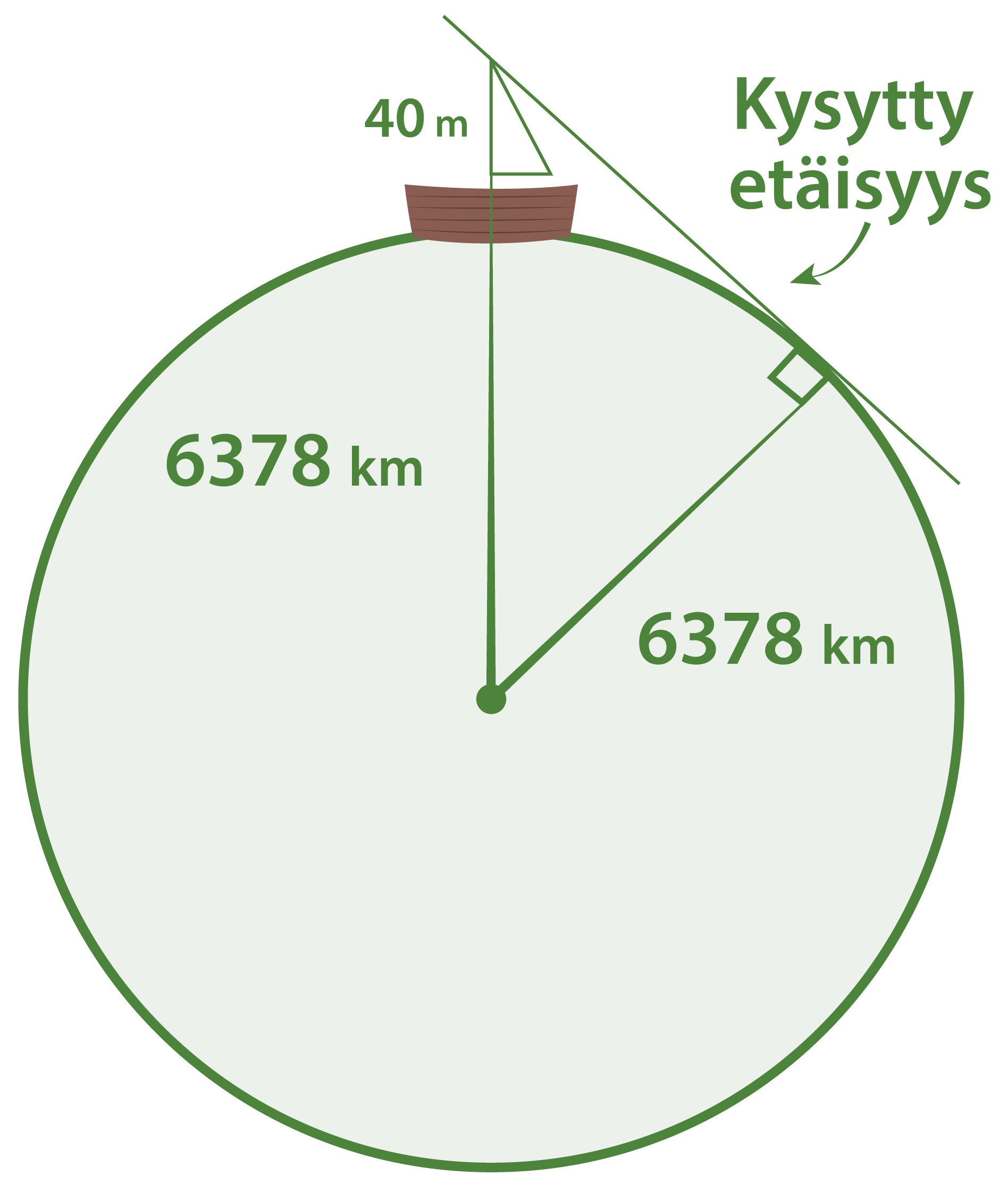
Pur­je­lai­van tä­hys­tys­kori si­jait­see 40 m kor­keu­des­sa. Las­ke­taan kuin­ka kau­ak­si siel­tä voi näh­dä tyy­nel­lä sääl­lä. Maa­pal­lon säde on 6378 km. (ku­van mit­ta­suh­teet ei­vät ole oi­kein).

Ku­vi­oon muo­dos­tuu suo­ra­kul­mai­nen kol­mio, jon­ka toi­nen ka­tee­teis­ta on ky­syt­ty etäi­syys. Hy­po­te­nuu­san pi­tuus on 6378 km + 0,040 km = 6378,040 km.

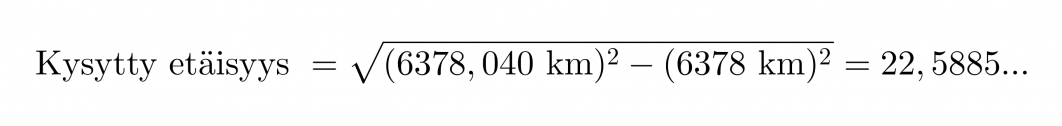
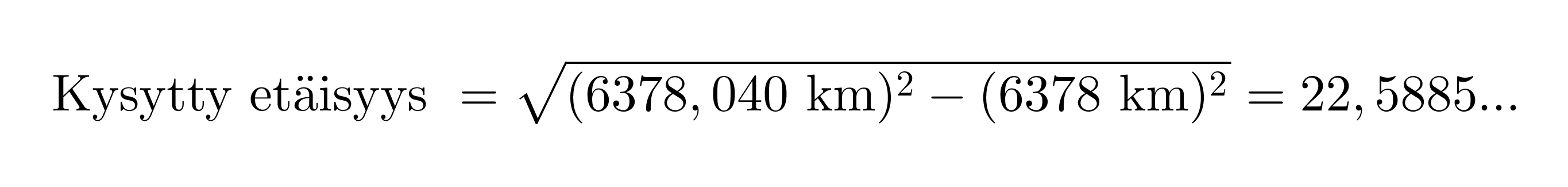
Klik­kaa kuva suu­rem­mak­si!

Vas­taus: Tä­hys­tys­tor­nis­ta voi näh­dä 23 km pää­hän.

Huom! To­del­li­suu­des­sa mat­ka mi­ta­taan maa­pal­lon pin­taa pit­kin eli täs­sä pi­täi­si las­kea sek­to­rin kaa­ren pi­tuus, mut­ta kos­ka sek­to­rin kes­kus­kul­ma on hy­vin pie­ni, on oi­ke­a­kin tu­los kilo­met­rien tark­kuu­del­la sama.

Klik­kaa kuva suu­rem­mak­si!