15. Ympyrän kehä- ja keskuskulma
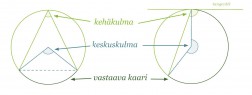
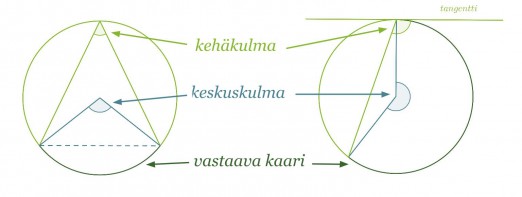
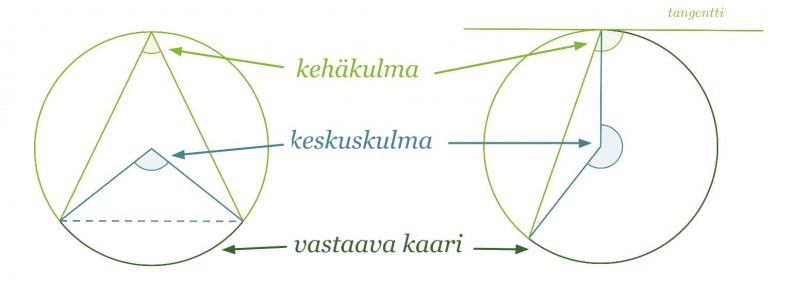
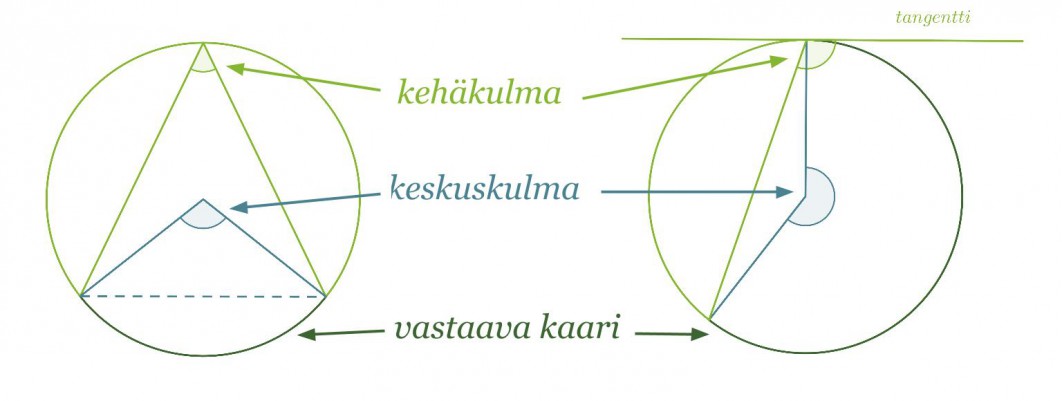
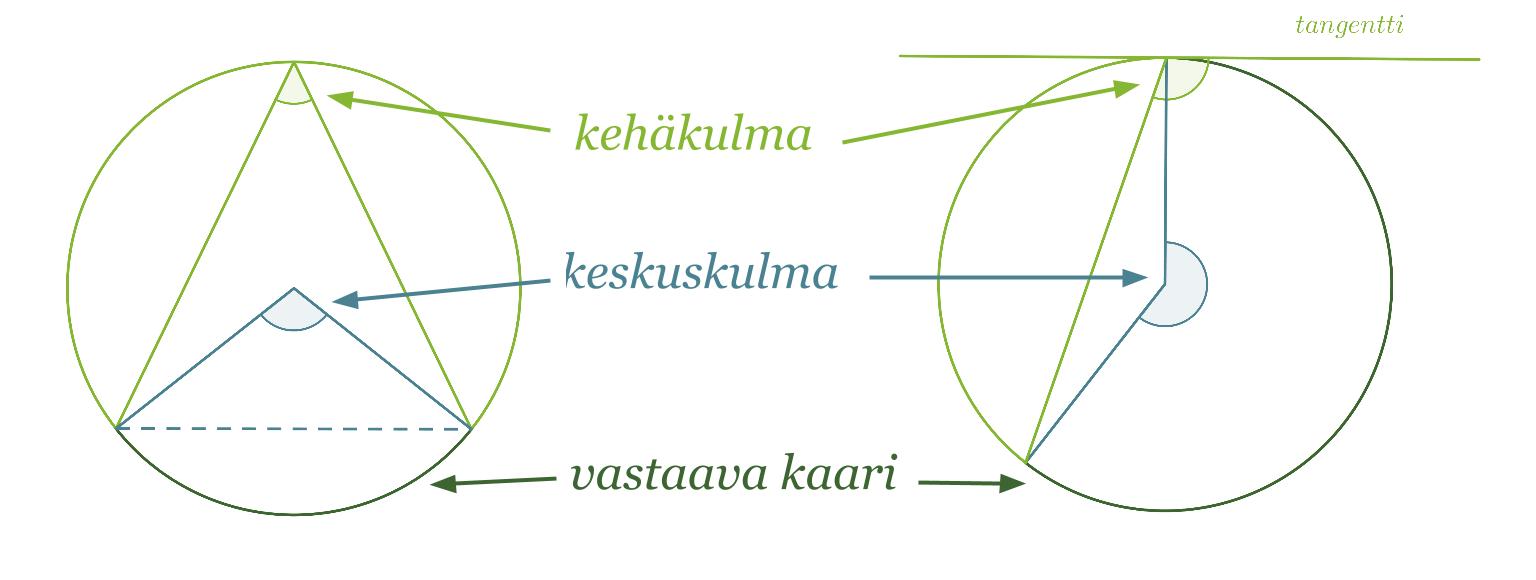
Ympyrän kehäkulma on kulma, jonka kärki on ympyrän kehällä ja jonka kylkinä on kaksi jännettä tai jänne ja tangentti. Kehäkulman kylkien väliin jäävä kehän osa on kehäkulmaa vastaava kaari. Kehäkulmaa vastaava keskuskulma puolestaan sijaitsee ympyrän keskipisteessä ja sen kyljet erottavat ympyrästä kehäkulmaa vastaavan kaaren.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
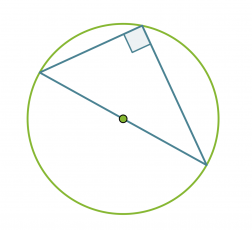
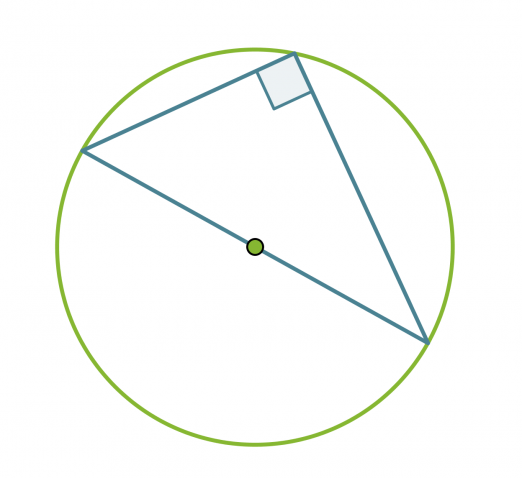
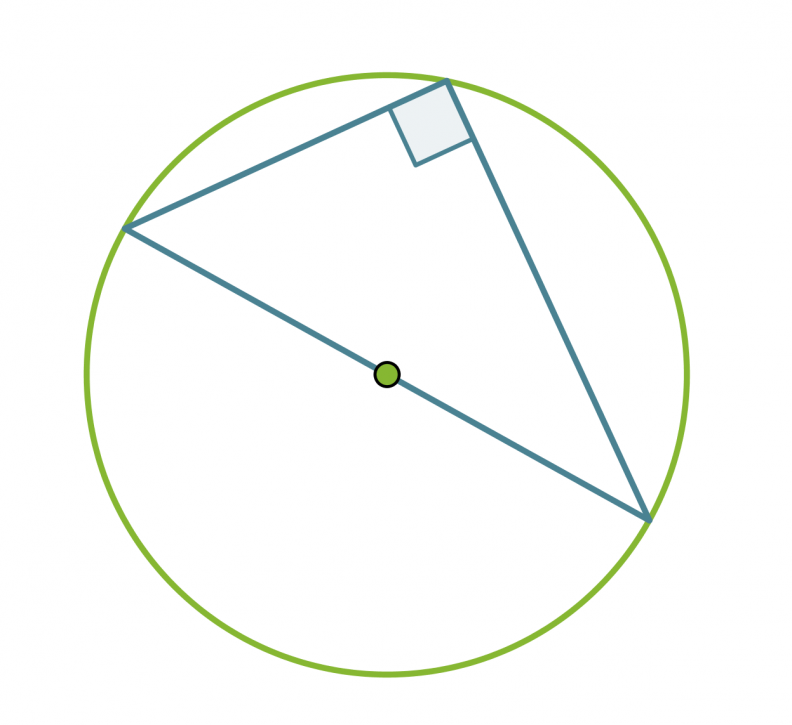
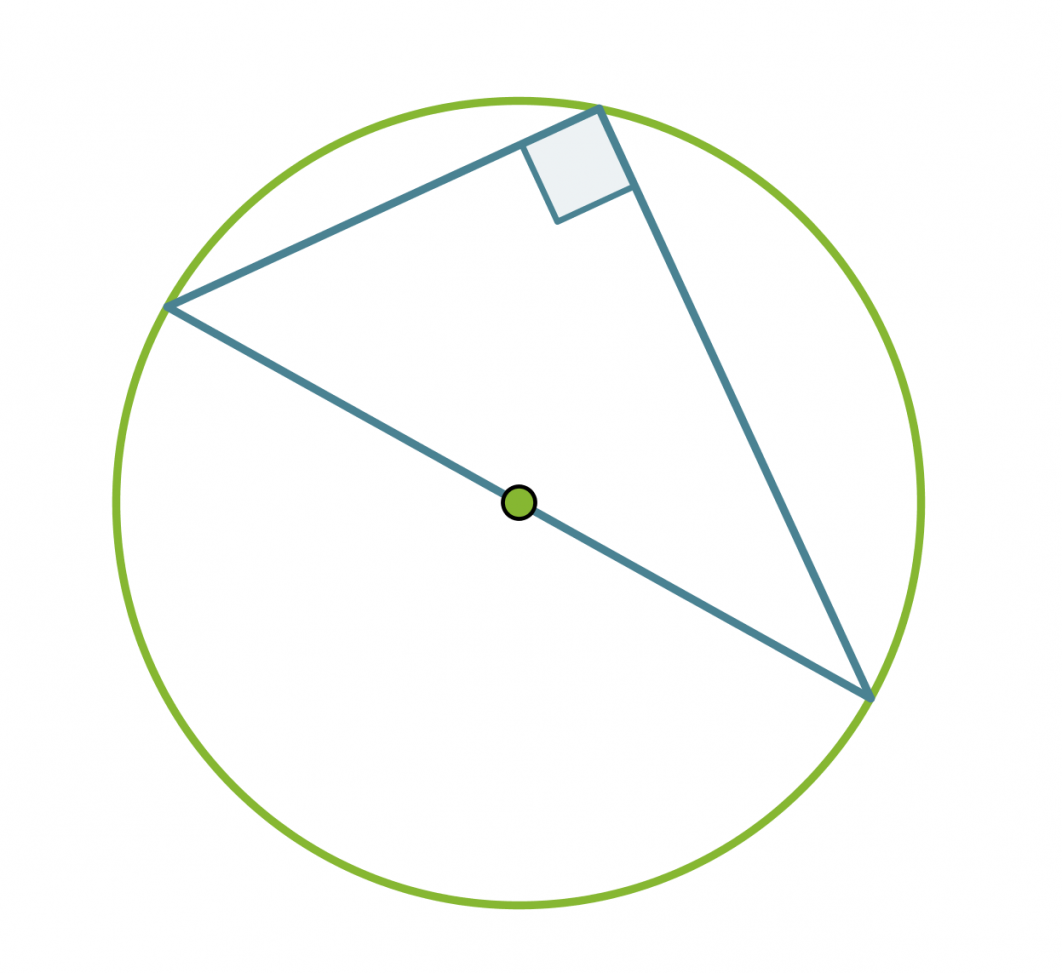
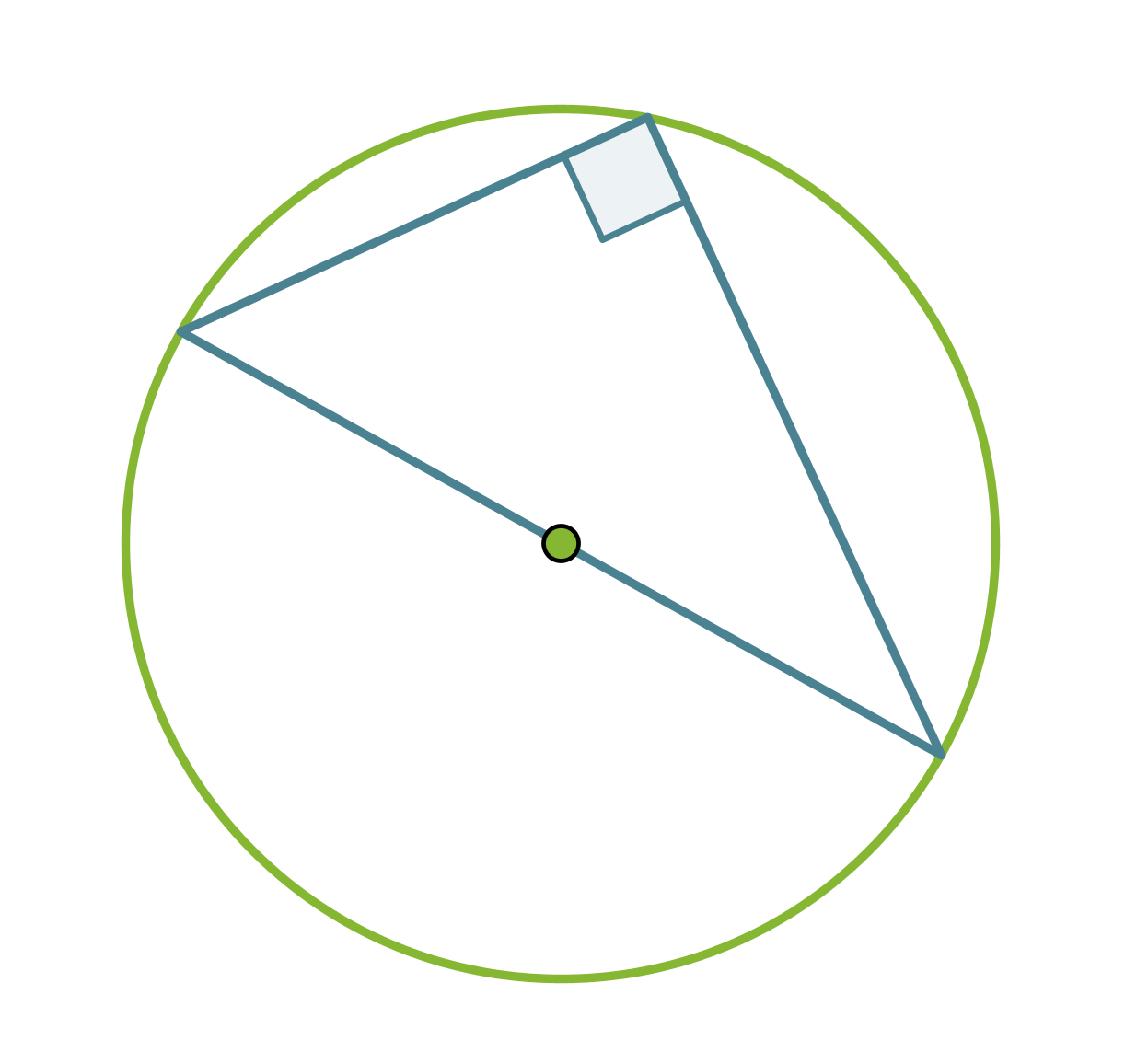
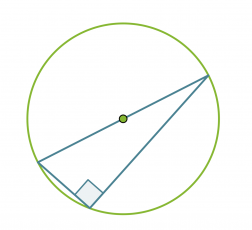
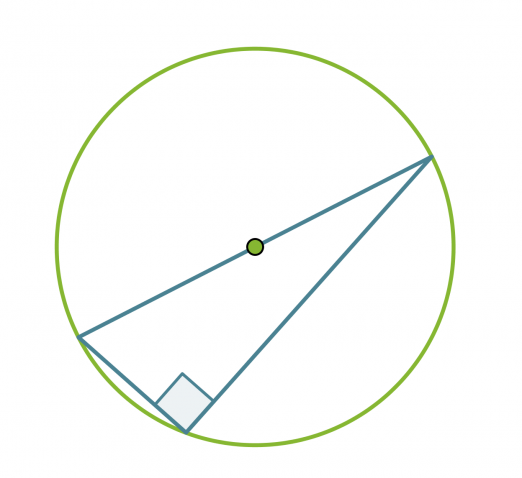
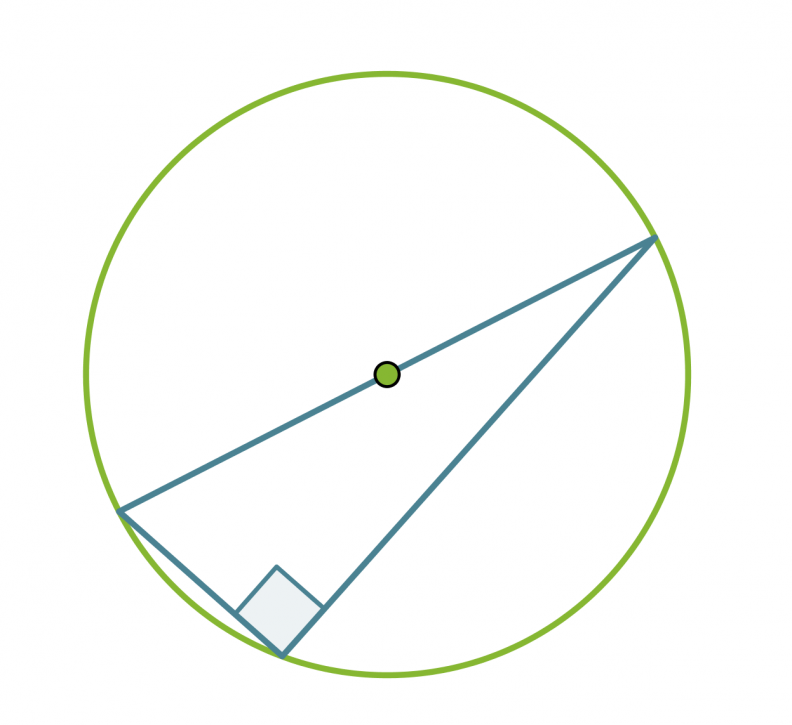
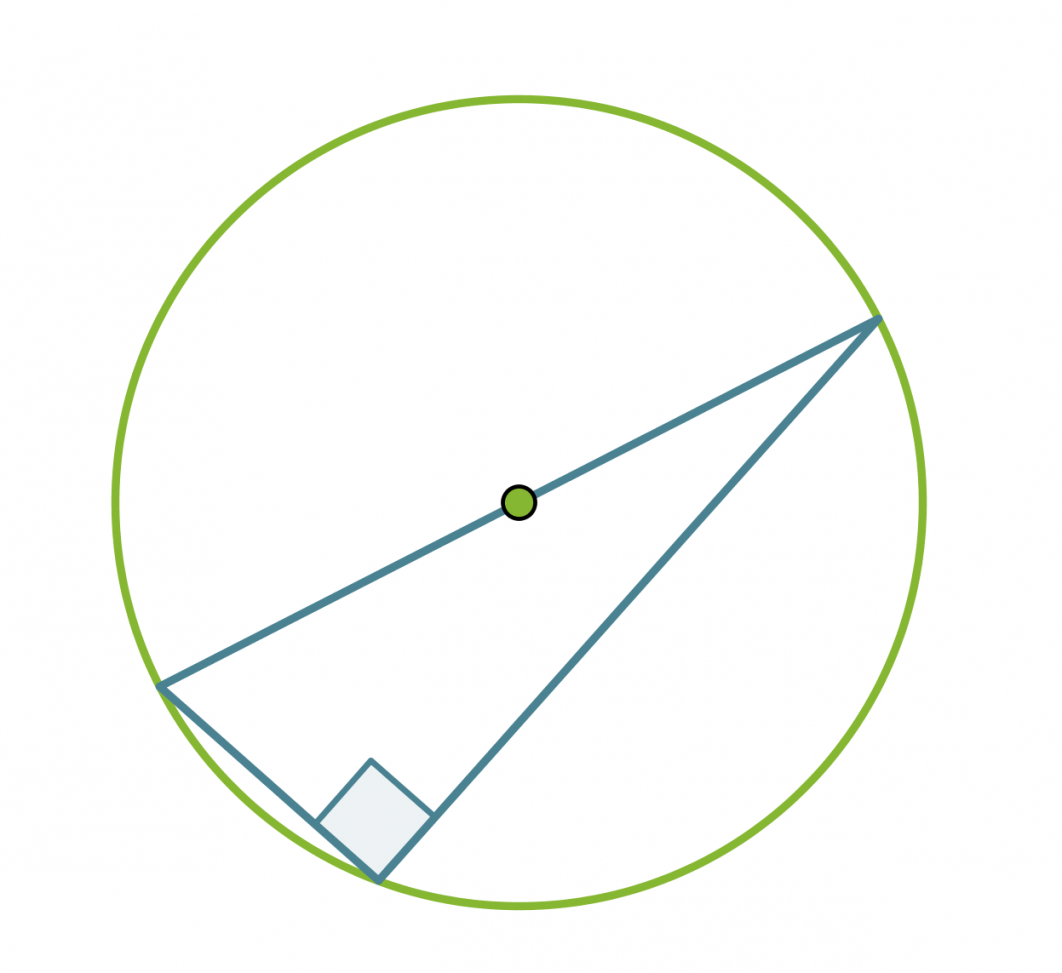
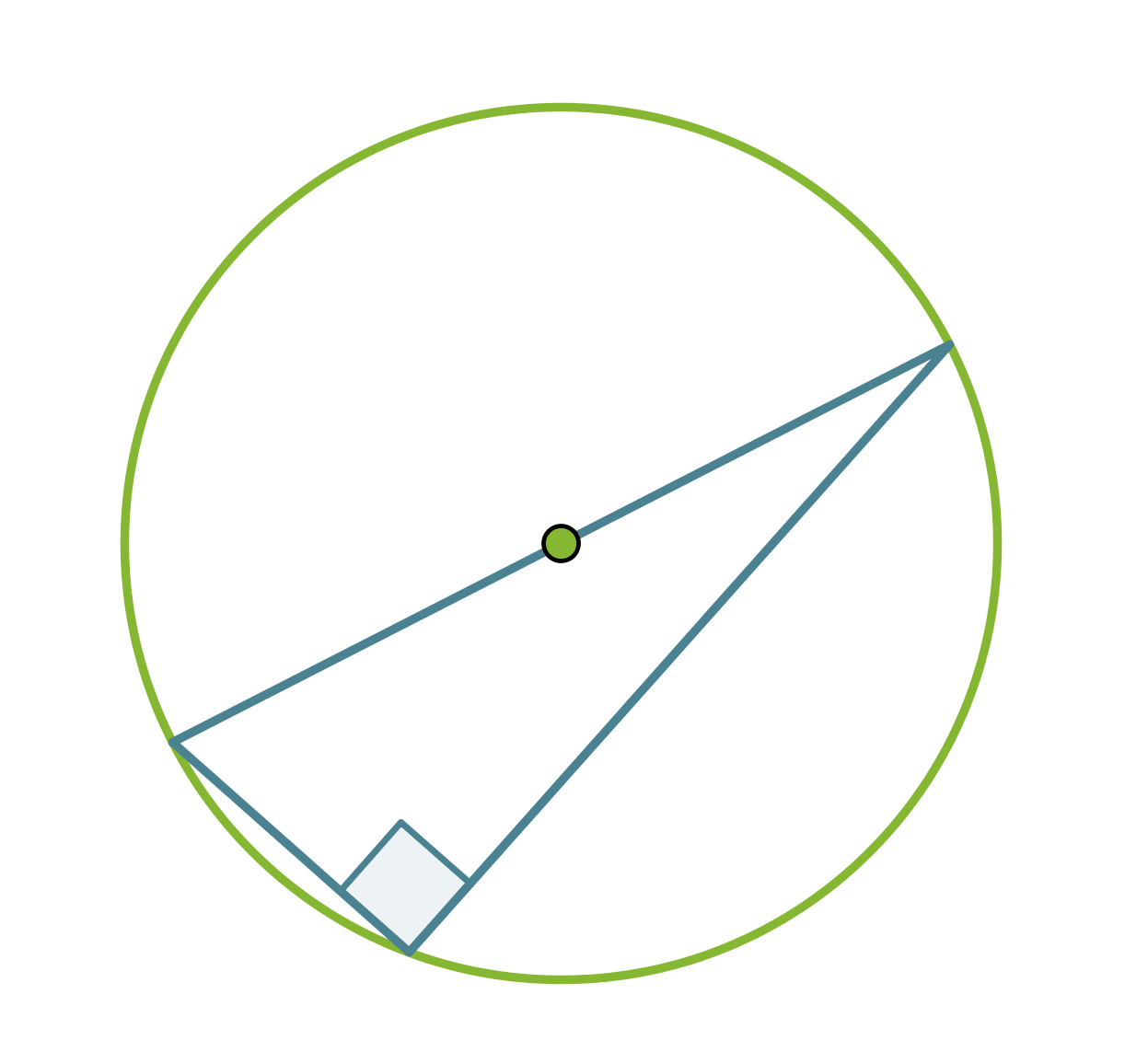
Thalesin lause: Ympyrän halkaisijan päätepisteistä kehälle samaan pisteeseen piirretyt janat ovat kohtisuorassa toisiaan vastaan. Tosin sanoen puoliympyrän kaaren sisältämä kulma on suora.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
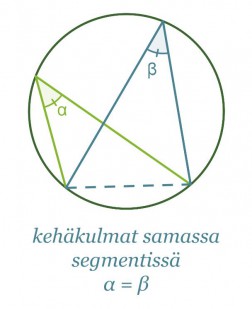
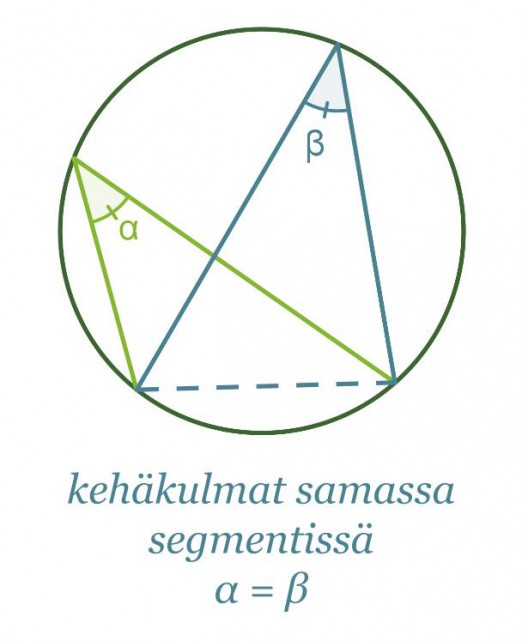
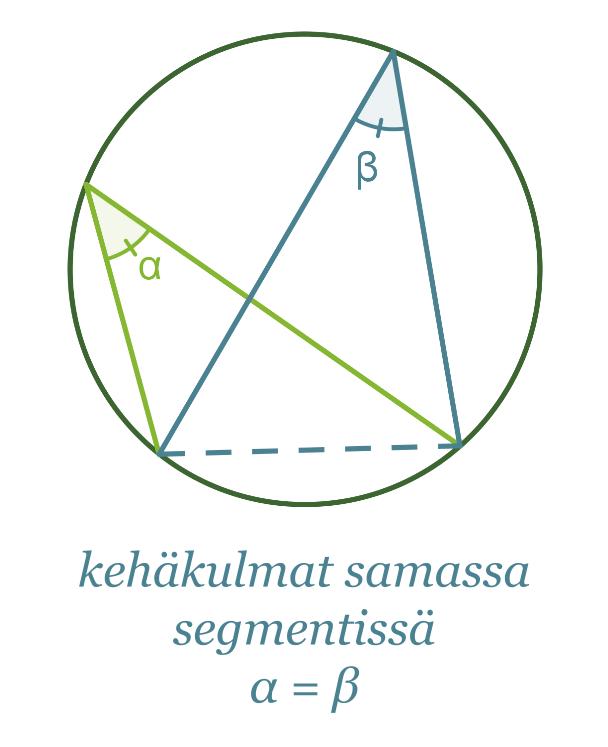
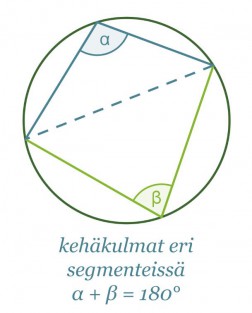
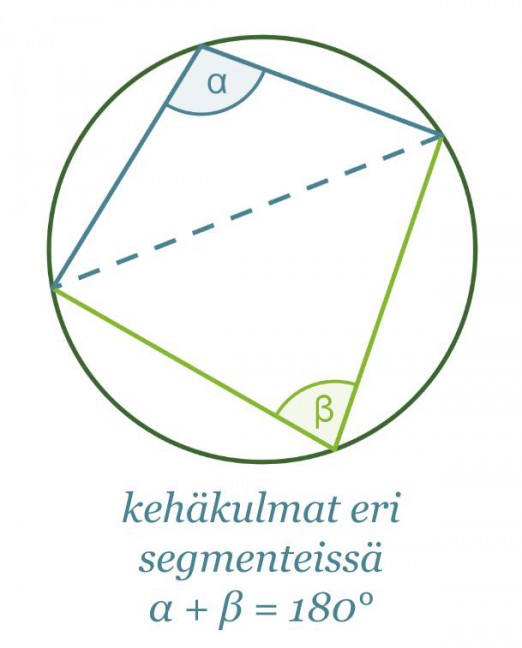
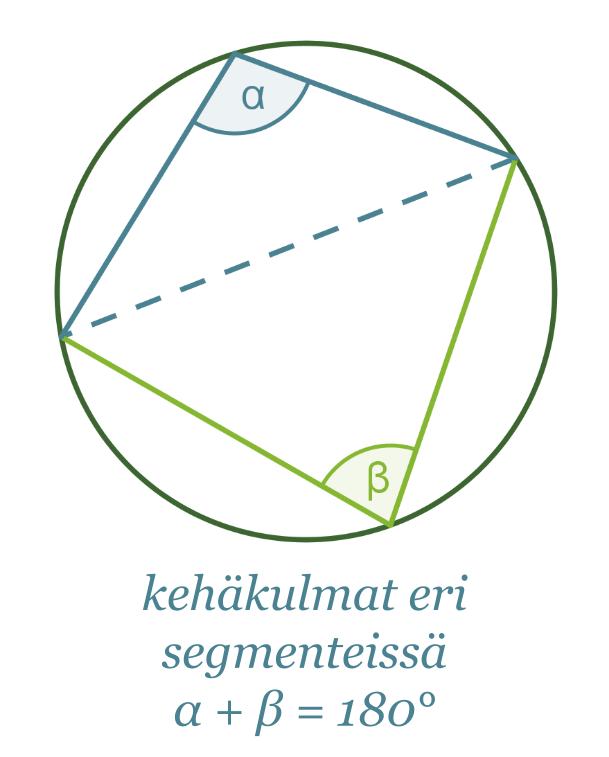
Jos kehäkulma piirretään joltain muulta ympyrän jänteeltä kuin halkaisijalta, ei kehäkulma ole 90°. Samalta jänteeltä ympyrän kehälle piirretyt kehäkulmat ovat kuitenkin aina yhtä suuret, jos kehäkulmat sijaitsevat samalla jänteen jakamalla segmentillä eli samalla puolella jännettä. Jos samasta ympyrän jänteestä piirretään kaksi kehäkulmaa siten, että ne sijaitsevat eri segmenteissä, on kehäkulmien summa 180°.
Samaa kaarta vastaavat kehäkulmat ovat yhtä suuret.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
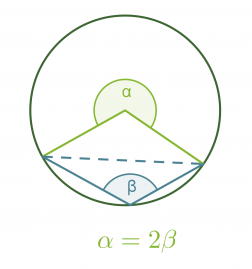
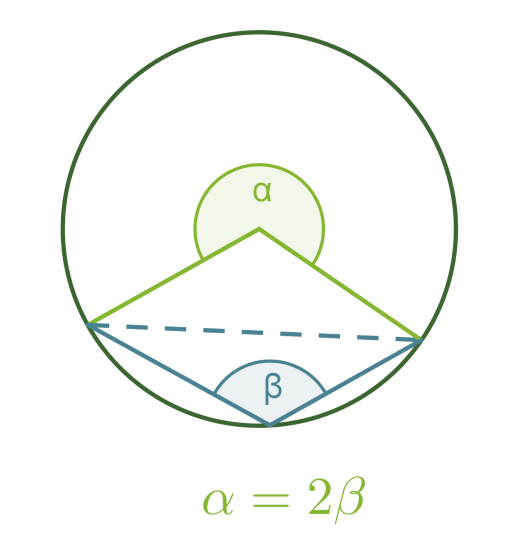
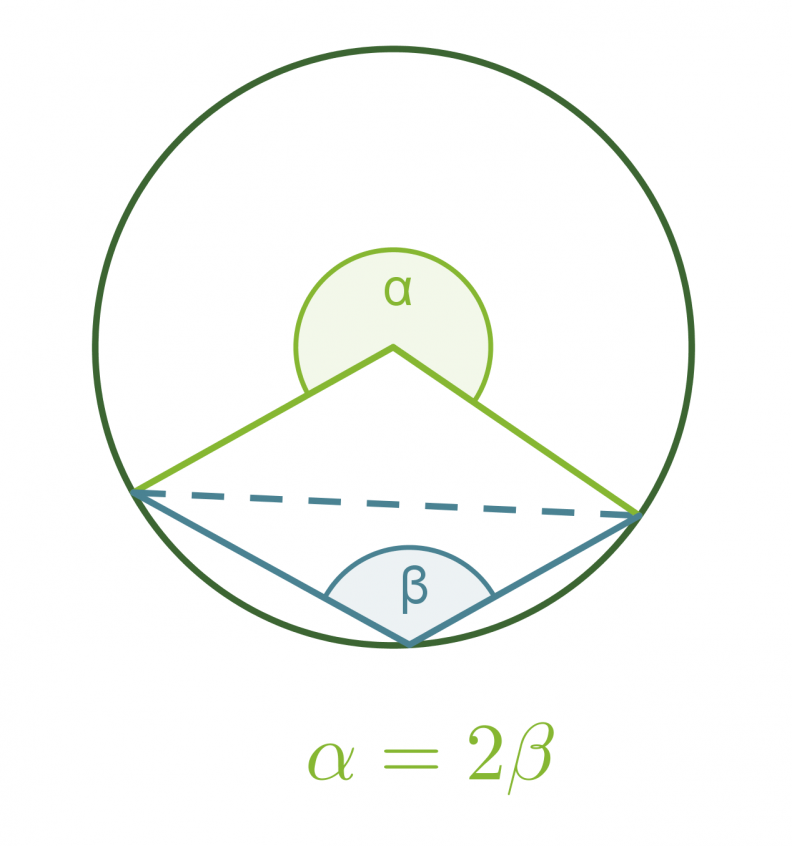
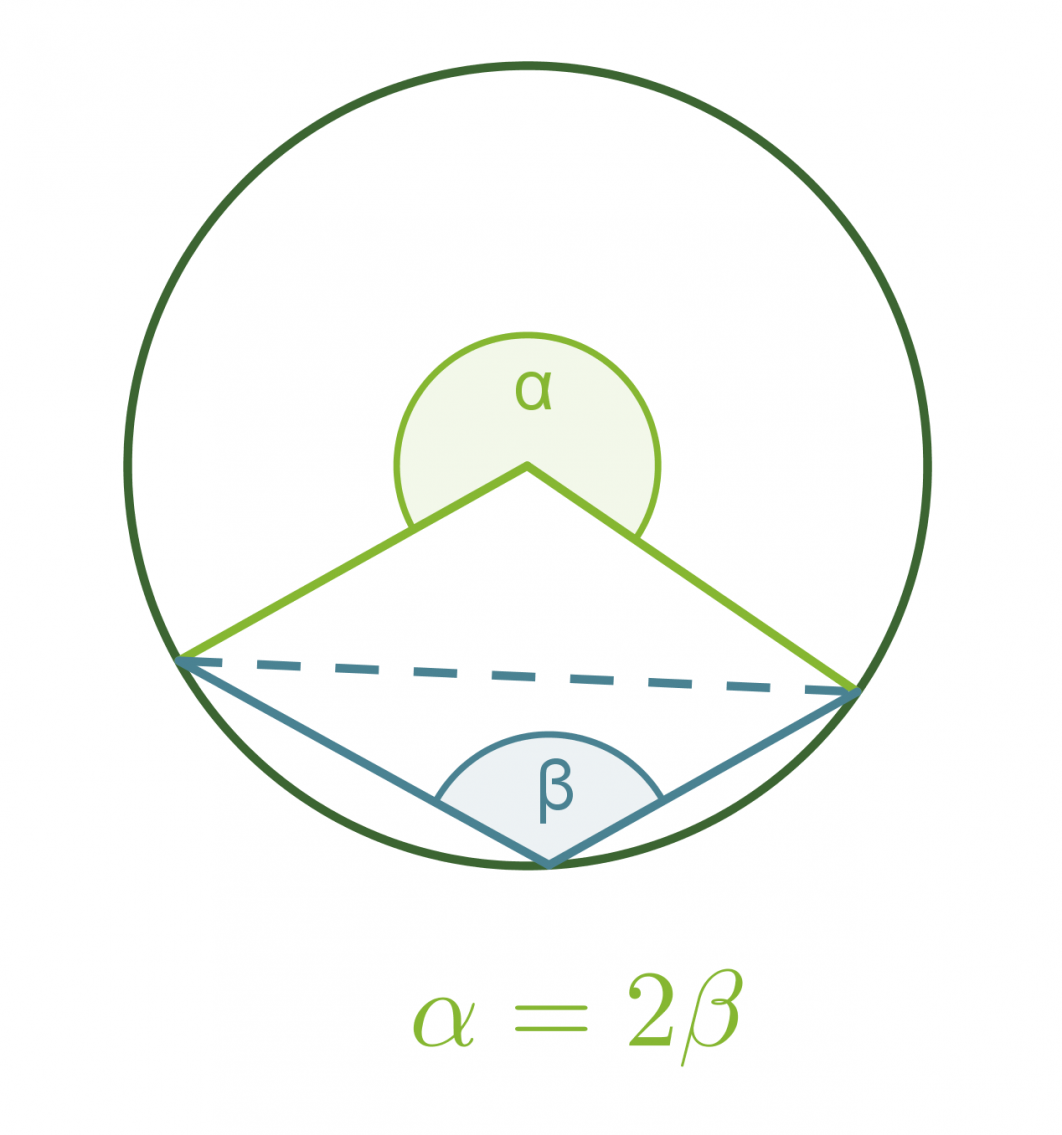
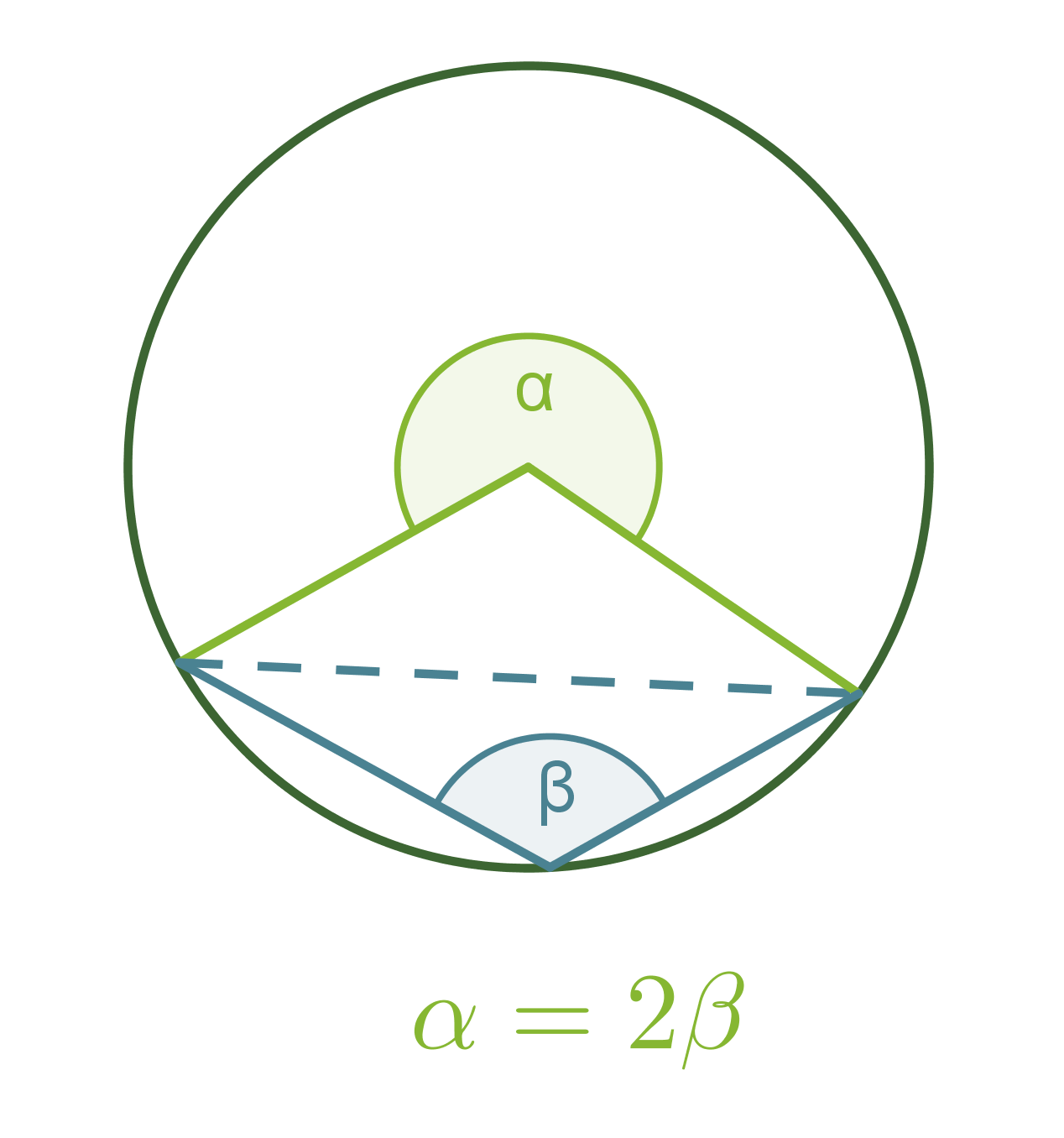
Kehäkulmalause
Samalla ympyrän jänteellä sijaitseva keskuskulma on kaksi kertaa niin suuri kuin sitä vastaava kehäkulma.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
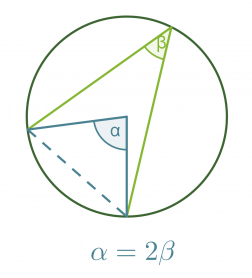
Klikkaa kuva suuremmaksi!
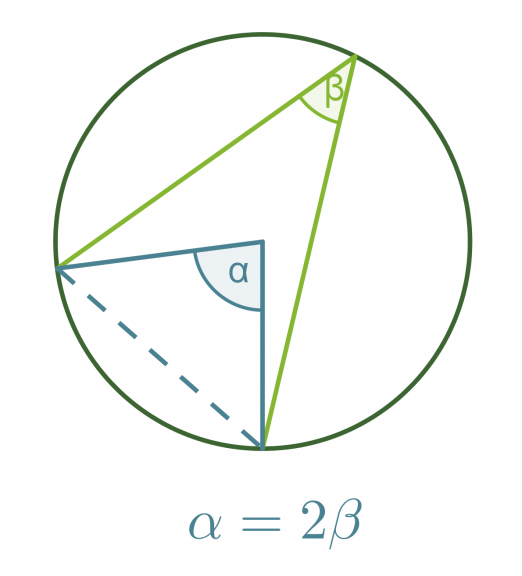
Klikkaa kuva suuremmaksi!
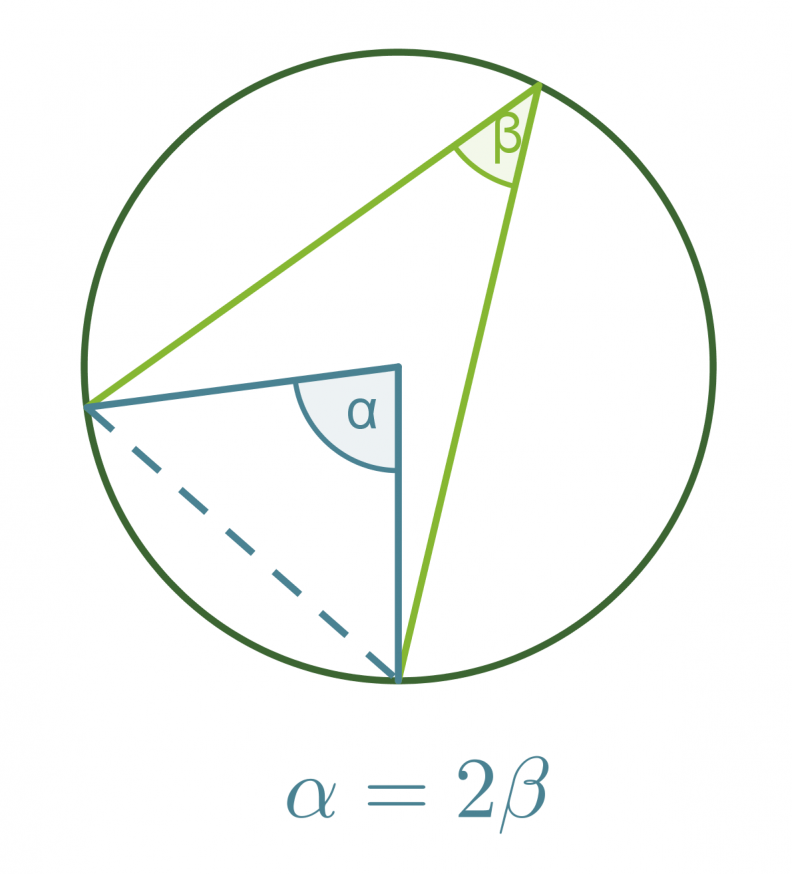
Klikkaa kuva suuremmaksi!
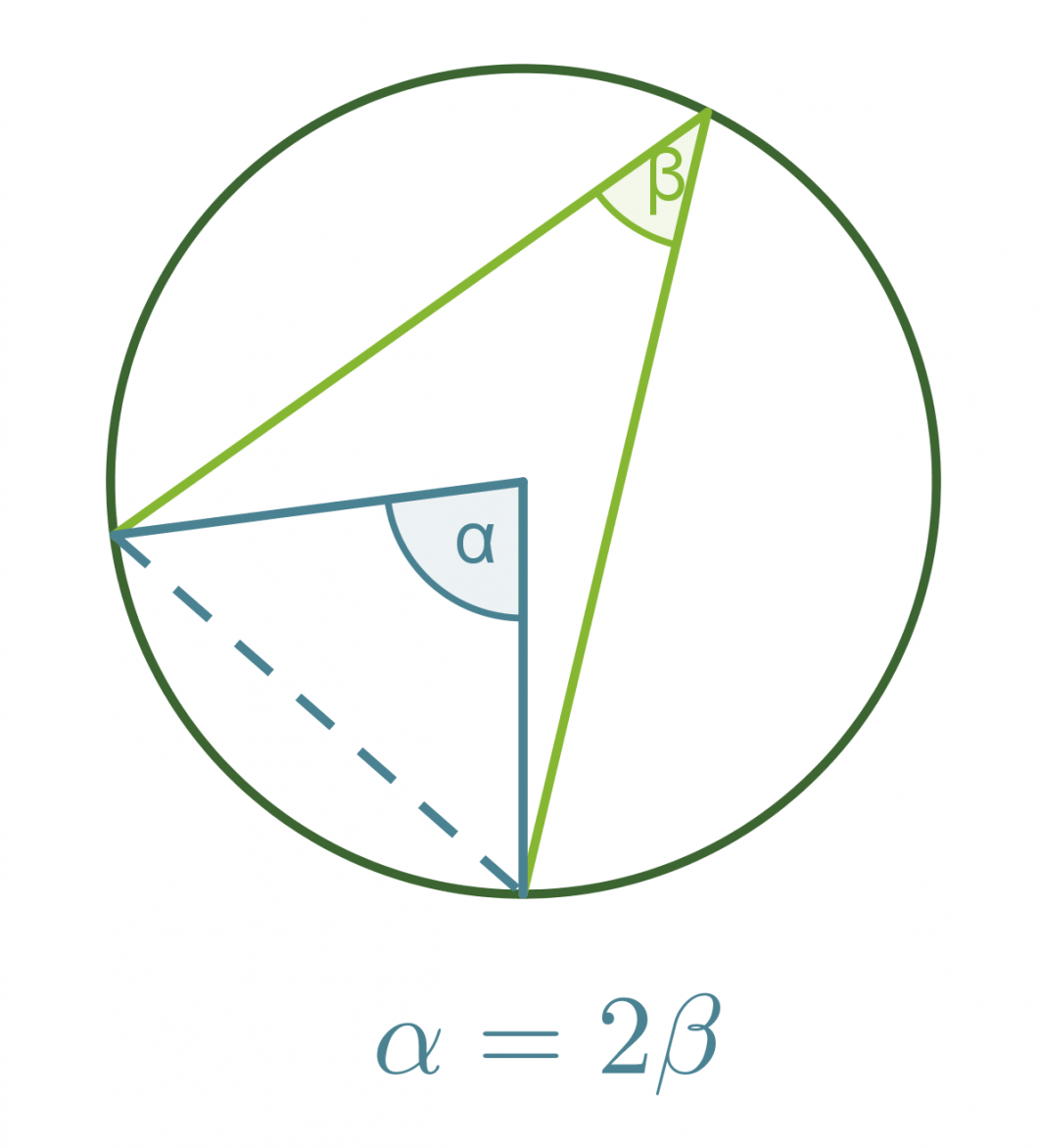
Klikkaa kuva suuremmaksi!
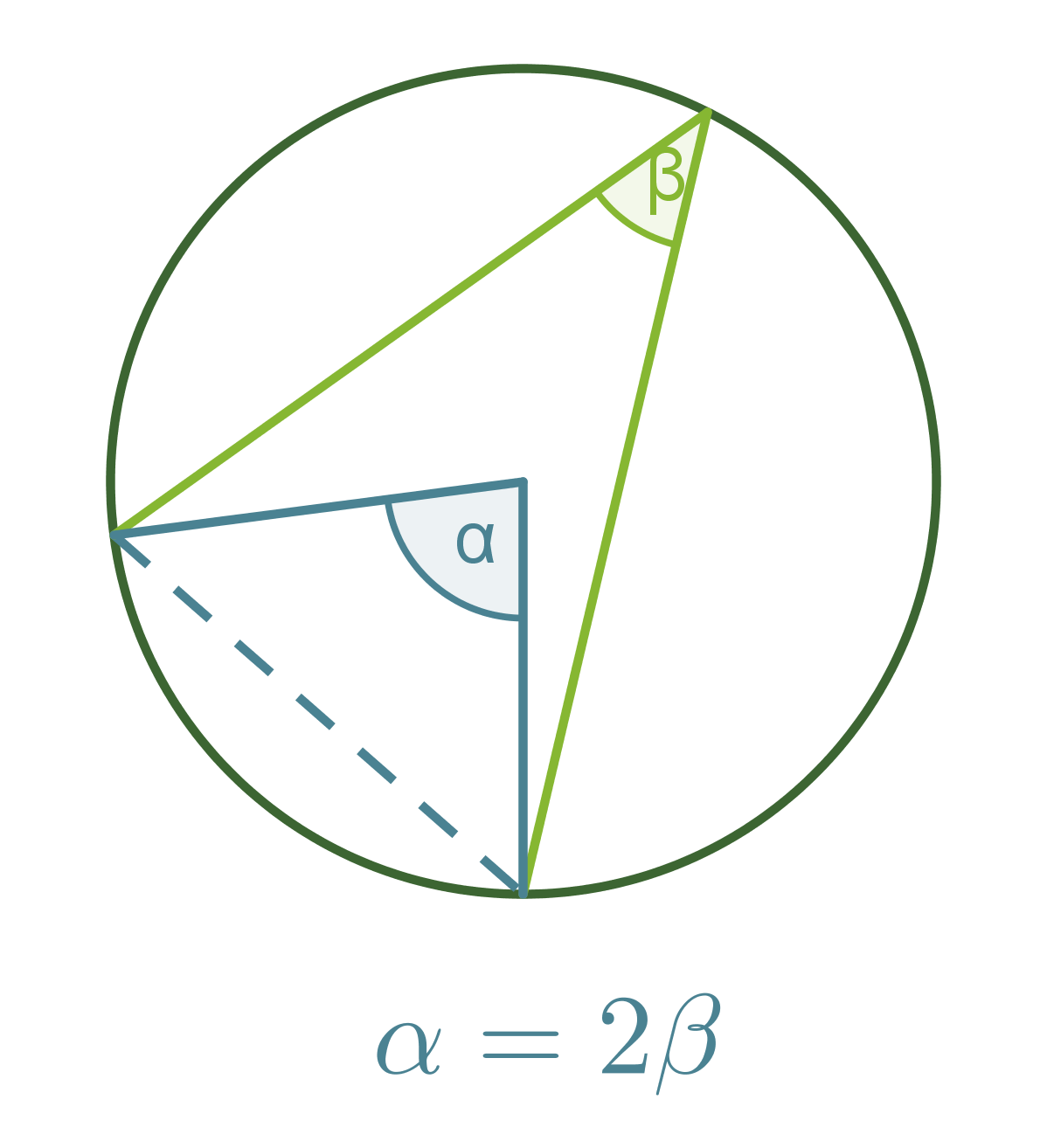
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
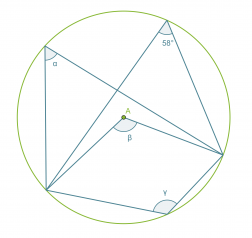
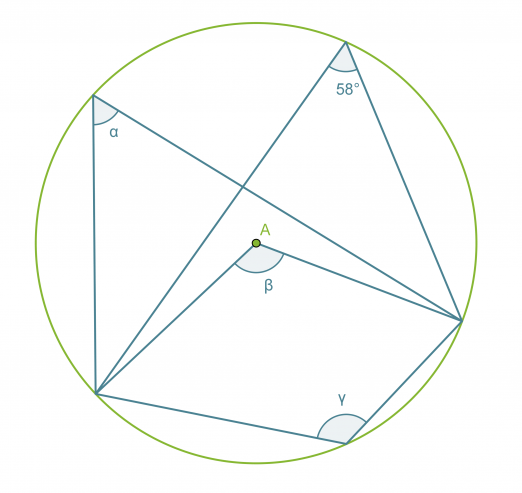
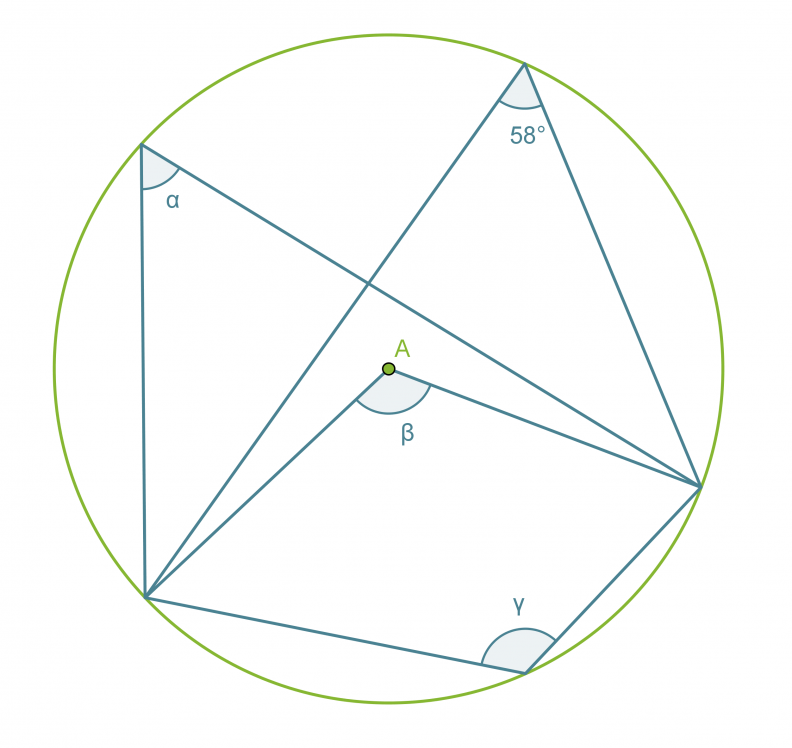
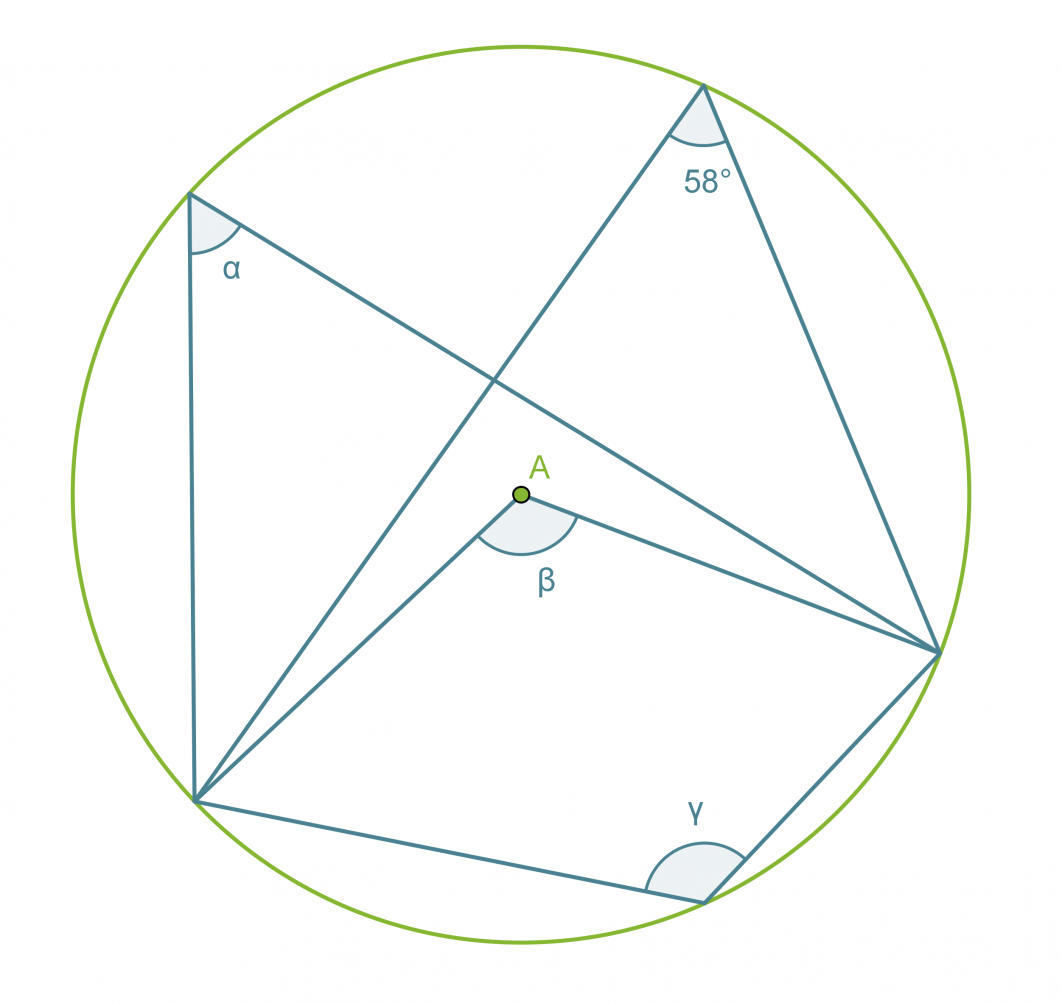
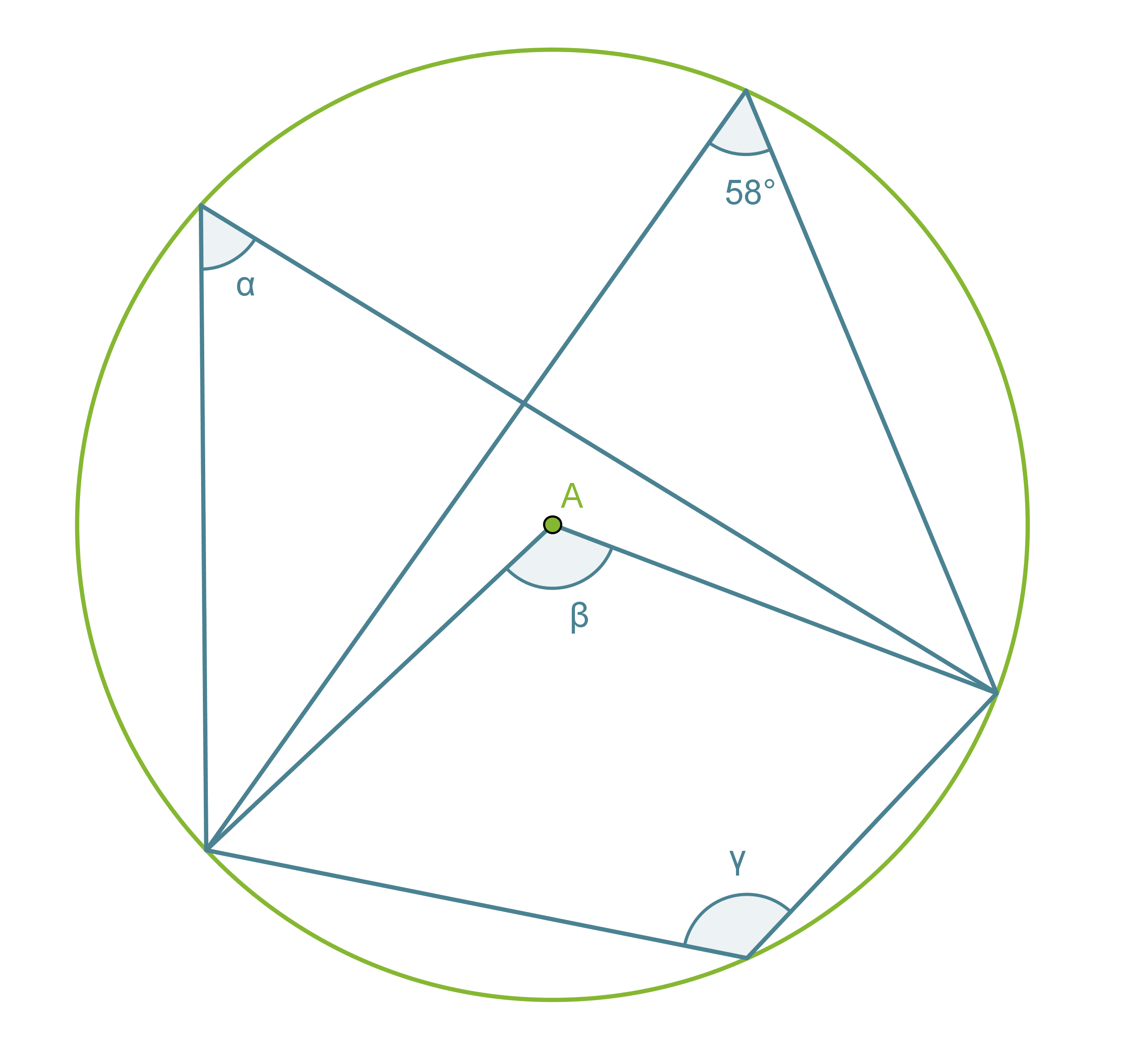
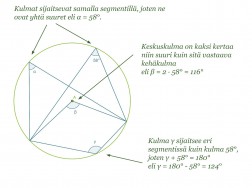
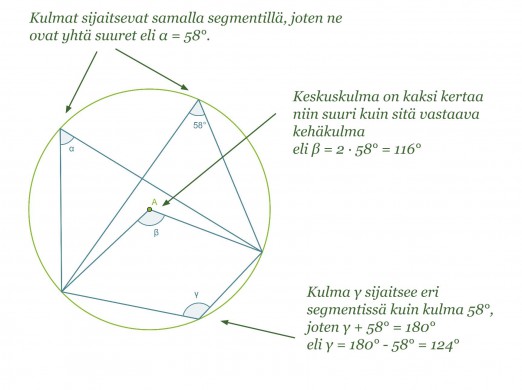
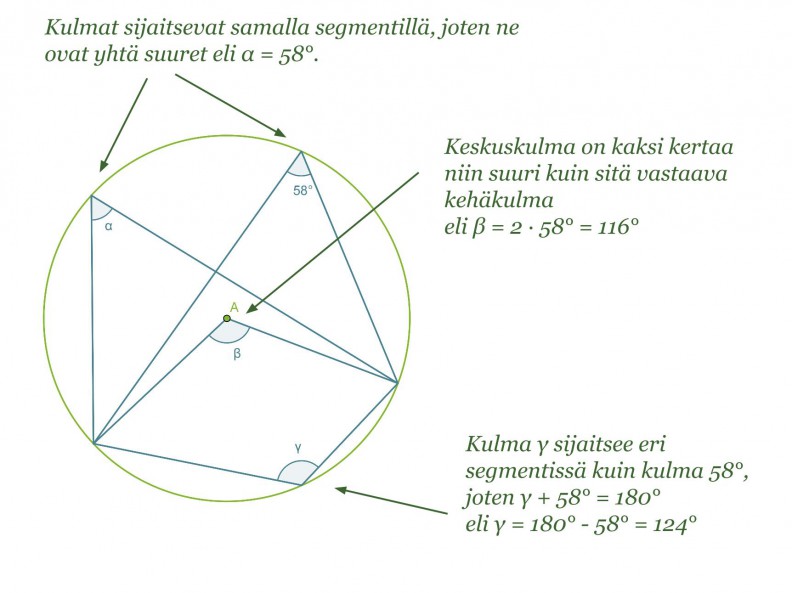
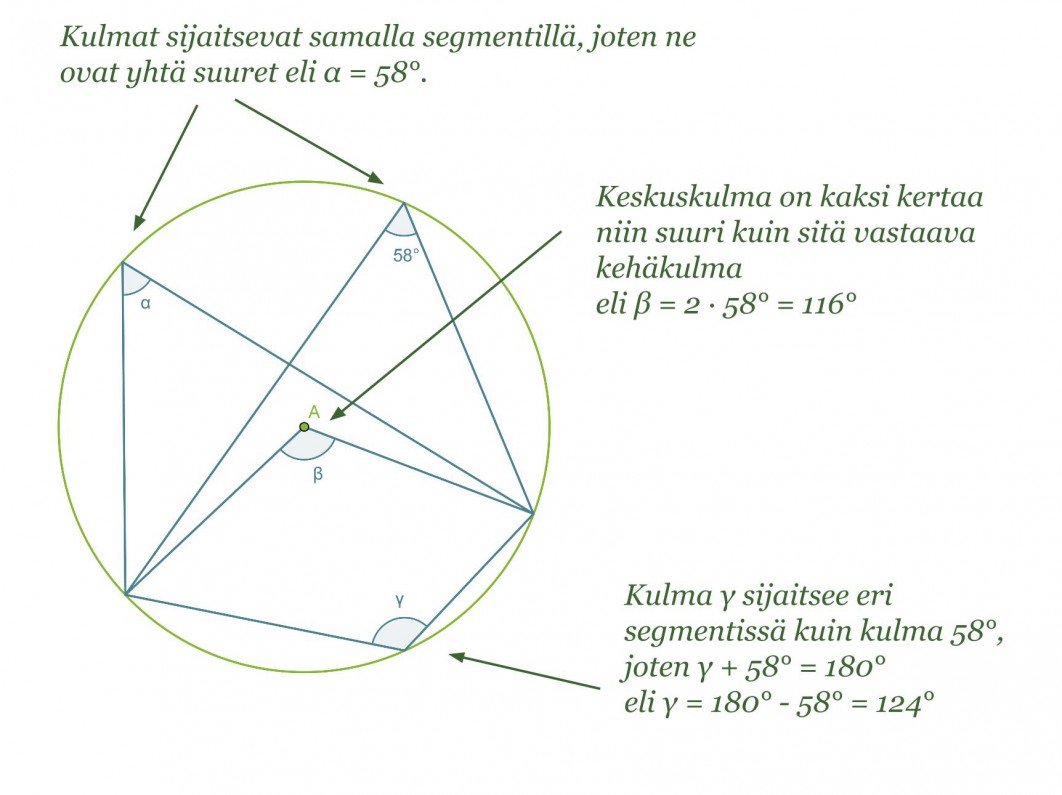
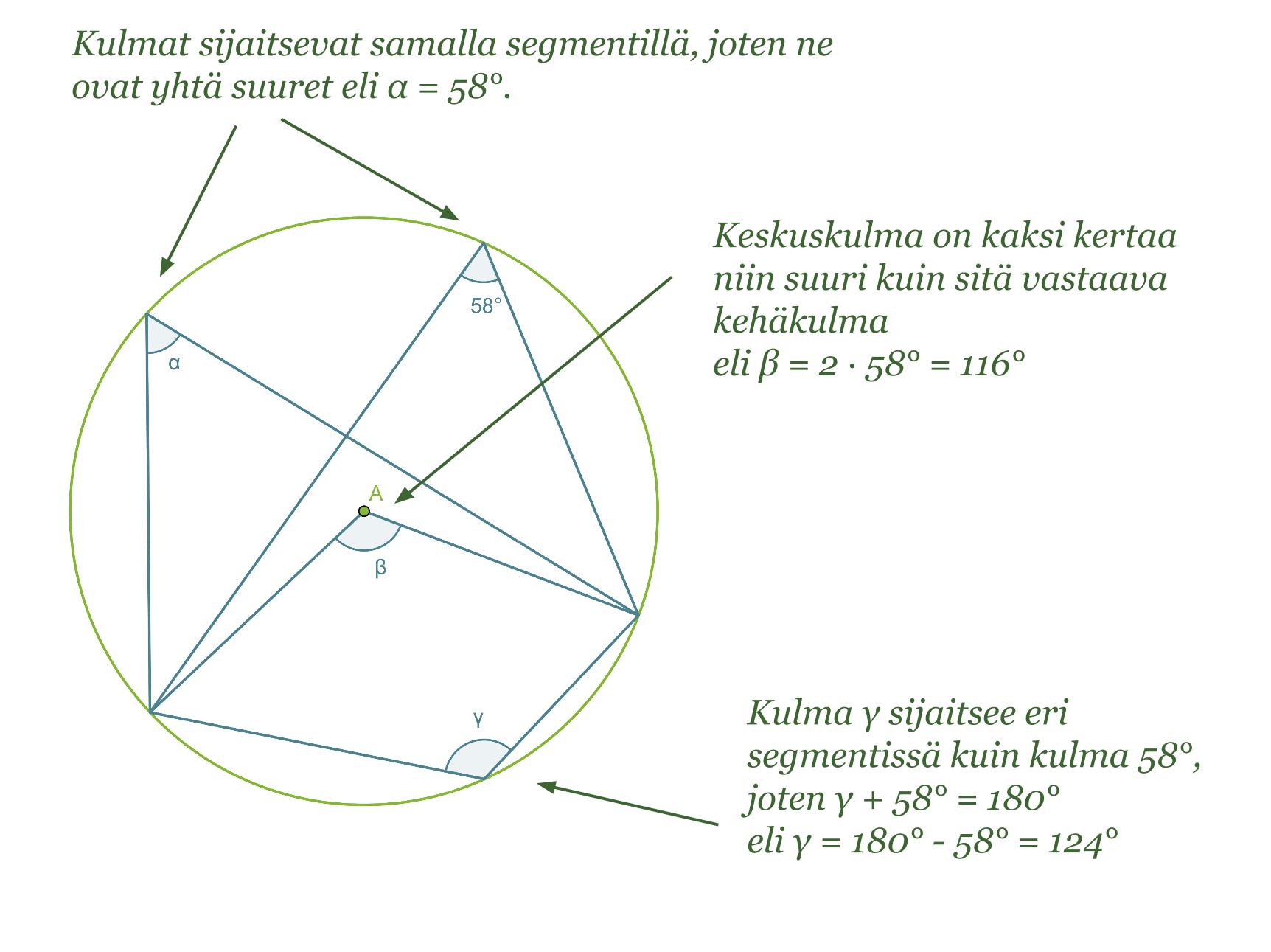
Esimerkki 1.
Määritetään kulmien α, β ja γ suuruudet.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Koska kaikki kehäkulmat ja keskuskulma on piirretty samalta ympyrän jänteeltä, voidaan soveltaa äsken esiteltyjä lauseita.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: α = 58º, β = 116º ja γ = 124º.
Avoin matematiikka 8Osio 3: Tasogeometriaa5.6.2014