1. Funktiokone

Funk­ti­o­kone on ra­ken­net­tu tiet­tyä toi­min­taa var­ten ja se toi­mii aina tie­tyn sään­nön mu­kai­ses­ti. Funk­ti­o­kone voi esi­mer­kik­si olla purk­ka-au­to­maat­ti, joka muun­taa ko­li­kot tie­tyk­si purk­ka­mää­räk­si. Uu­teen asun­toon muu­tet­ta­es­sa moni toi­voi­si, että oli­si ole­mas­sa funk­ti­o­kone, joka pie­nen­täi­si huo­ne­ka­lut nuk­ke­ko­din huo­ne­ka­lu­jen ko­koi­sik­si. Täl­löin oli­si tie­tys­ti syy­tä löy­tyä myös kään­tei­ses­ti toi­mi­va funk­ti­o­kone, jot­ta muut­to­ta­va­rat saa­tai­siin jäl­leen nor­maa­liin ko­koon­sa.

Esimerkki 1.

Tar­kas­tel­laan funk­ti­o­ko­net­ta, joka en­sik­si ker­too sii­hen syö­te­tyt nu­me­rot kah­del­la, li­sää tu­loon vie­lä yh­den ja an­taa ko­nees­ta ulos tu­lok­se­na saa­dun lu­vun. Jos esi­mer­kik­si ko­nee­seen syö­te­tään luku kol­me, saa­daan tu­los­tee­na luku seit­se­män.

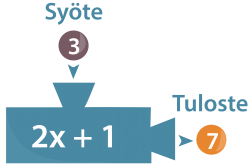
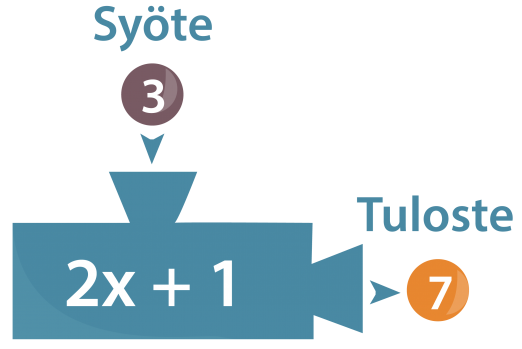
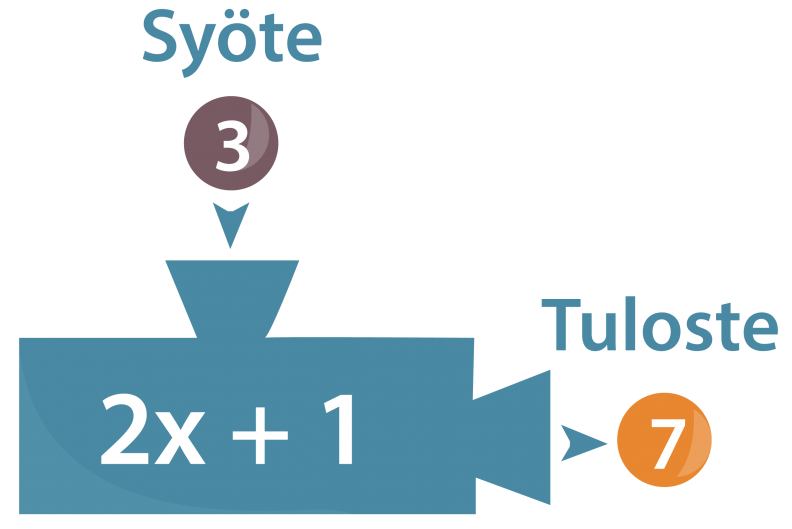
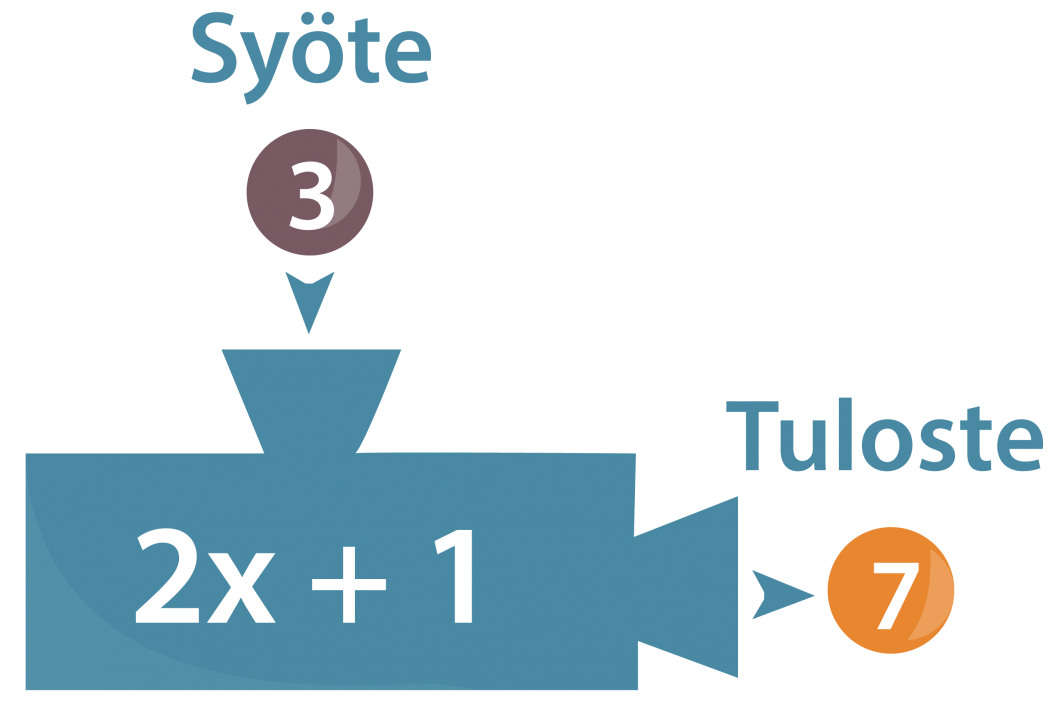
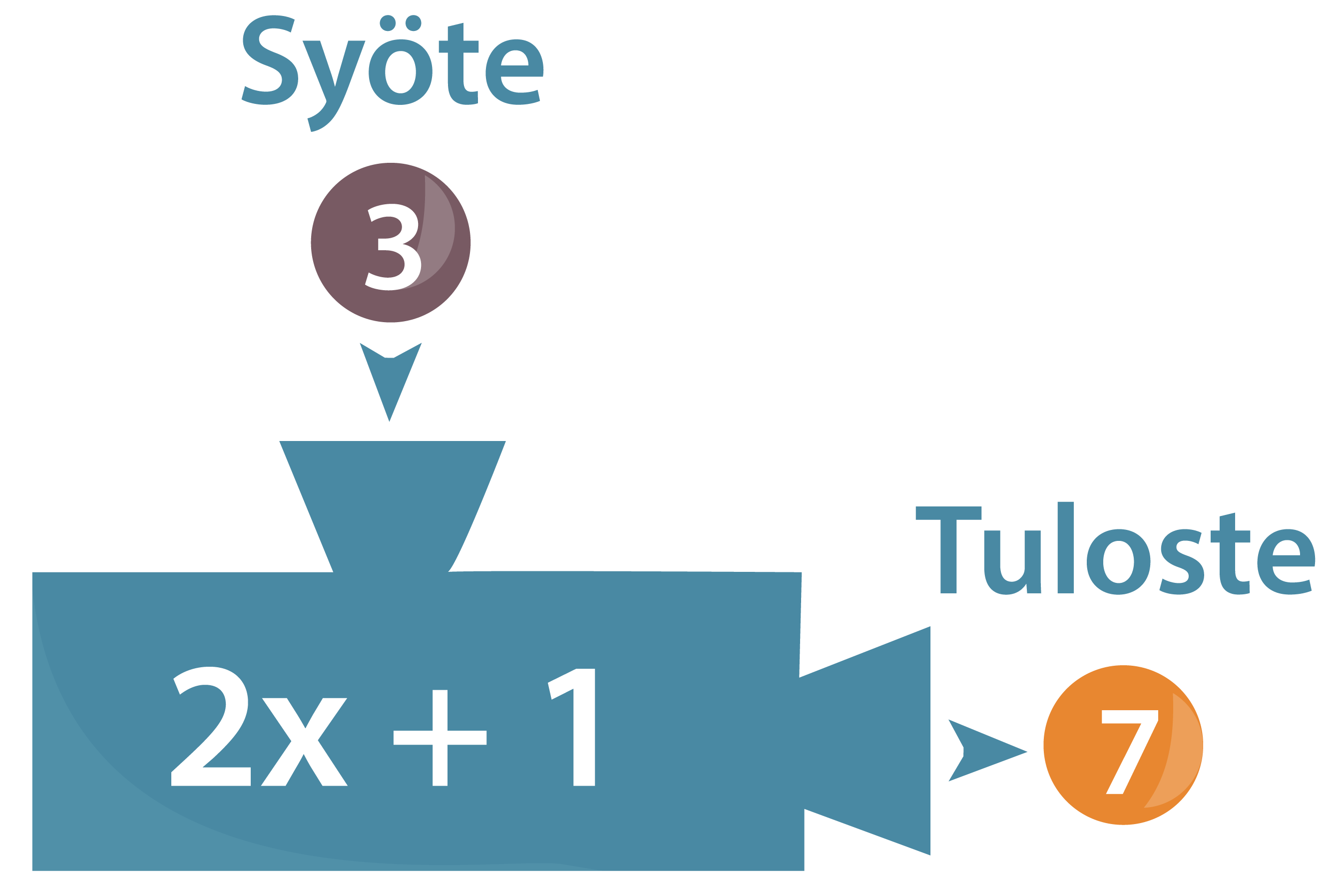
Ky­sei­nen funk­ti­o­kone on ha­lut­tu ra­ken­taa ra­jal­li­sek­si niin, että se pys­tyy vas­taan­ot­ta­maan ai­no­as­taan lu­vut 0, 1, 2, 3 ja 4. Ulos sii­tä sen si­jaan voi ”put­kah­taa” minä ta­han­sa koko­nais­luku nol­las­ta yh­dek­sään.

Si­sään syö­tet­tä­vien lu­ku­jen eli syöt­tei­den muut­tu­mi­nen tu­los­teek­si voi­daan ku­va­ta nuo­len avul­la:

• 0 →1 ”nol­la muut­tuu yk­kö­sek­si” tai
  ”nol­la ku­vau­tuu yk­kö­sek­si”
• 1 → 3 ”yksi ku­vau­tuu kol­mo­sek­si”
• 2 → 5 ”kak­si ku­vau­tuu vii­to­sek­si”
• 3 → 7 ”kol­me ku­vau­tuu seit­se­mäk­si”
• 4 → 9 ”nel­jä ku­vau­tuu yh­dek­säk­si”

Ylei­ses­ti voi­daan funk­ti­o­ko­neen toi­min­ta­tapa esit­tää ku­vauk­se­na

x → 2x + 1   eli     ”x ku­vau­tuu lau­sek­keek­si 2x + 1”

Funk­ti­o­ko­nei­ta voi olla usei­ta eri­lai­sia, jot­ka kaik­ki toi­mi­vat eri ta­val­la. Mi­kään niis­tä ei kui­ten­kaan toi­mi mi­ten sat­tuu, vaan aina eh­dot­to­mas­ti sa­man sään­nön mu­kaan. Jo­kai­sel­le funk­ti­o­ko­neel­le pä­te­vät sa­mat toi­min­ta­peri­aat­teet.