2. Funktion määritelmä
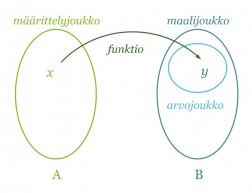
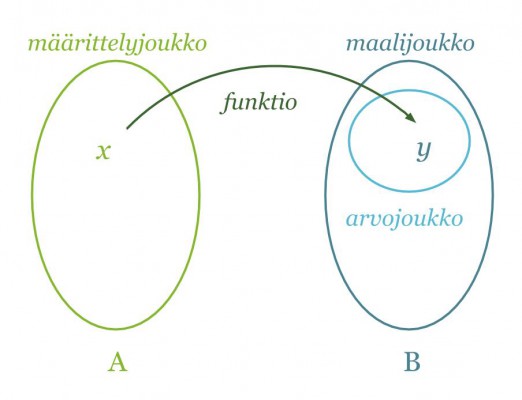
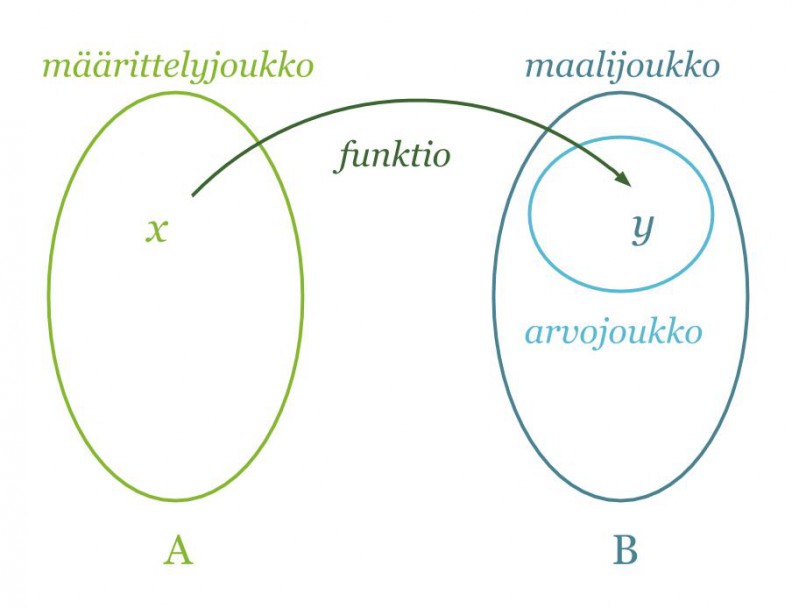
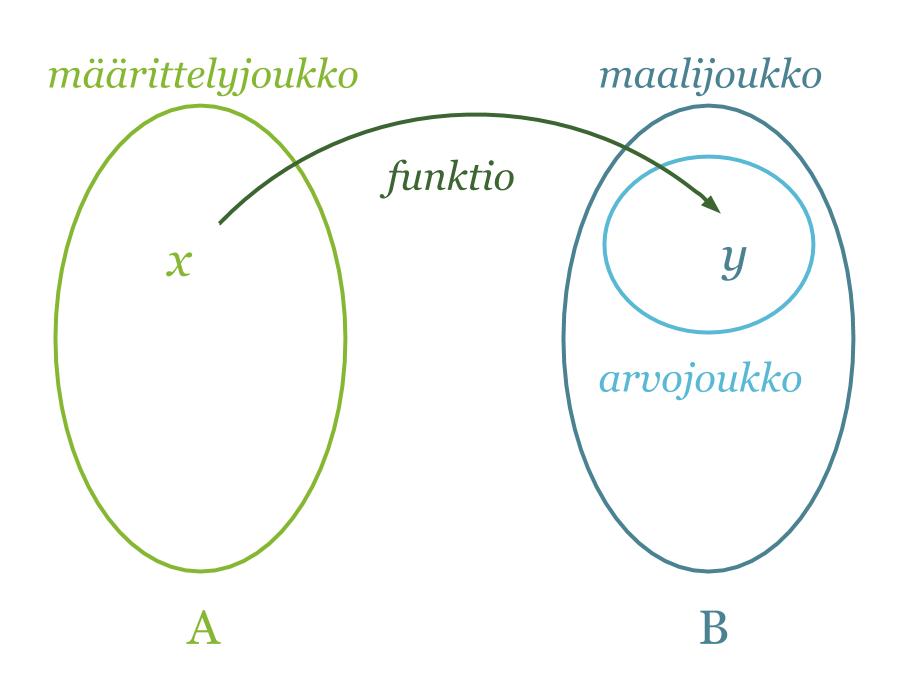
Funktio eli kuvaus f joukosta A joukkoon B on sääntö, joka liittää joukon A jokaiseen alkioon x joukosta B täsmälleen yhden alkion y.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jos y on x:n funktio, niin kaikki mahdolliset x:n arvot muodostavat funktion määrittelyjoukon eli lähtöjoukon ja kaikki mahdolliset y:n arvot vastaavasti maalijoukon. Funktion arvojoukko eli kuvajoukko on puolestaan funktion arvojen joukko, joka on saatu käyttämällä eri x:n arvoja. Arvojoukko on maalijoukon osajoukko. Matemaattisissa esimerkeissä joukot ovat usein lukujoukkoja, mutta reaalimaailman ilmiöitä kuvaavissa tehtävissä joukot voivat muodostua mistä tahansa, esimerkiksi eläimistä.
Funktion lauseketta merkitään usein y:n sijasta f(x):llä. Muuttujana on siis x ja funktion arvot määräytyvät tietyn säännön mukaan x:n arvojen perusteella. Asiayhteydestä riippuen funktiota ja muuttujaa merkitään myös muilla kirjaimilla. Jos kyseessä on esimerkiksi nopeus ajan funktiona, merkitän sitä yleensä v(t).
Esimerkki 1.
Mikä on edellisen kappaleen kuvauksen x → 2x + 1 määrittely-, arvo- ja maalijoukko?
Ratkaisu:
Kyseisen funktiokoneen toiminnasta sanottiin näin: ”Se pystyy ottamaan vastaan ainoastaan luvut 0, 1, 2, 3 ja 4. Ulos voi tulla mikä tahansa luku nollasta yhdeksään.”
Kuvauksen määrittelyjoukon eli lähtöjoukon muodostavat kaikki ne alkiot (tässä tapauksessa luvut), joita koneeseen voidaan syöttää eli 0, 1, 2, 3 ja 4. Maalijoukko muodostuu mahdollisesti ulostulevista luvuista, joita ovat 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9. Maalijoukko ei tarkoita sitä, että kaikki nämä luvut myös tulevat ulos koneesta. Ne luvut, jotka koneesta todella saadaan, ovat 1, 3, 5, 7 ja 9. Nämä muodostavat arvojoukon eli kuvajoukon. Arvojoukko muodostuu aina maalijoukon alkioista. Se voi sisältää kaikki maalijoukon alkiot tai niin kuin tässä tapauksessa, osan niistä.
Vastaus: Kuvauksen x → 2x + 1 määrittelyjoukko on {0, 1, 2, 3, 4}, arvojoukko on {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ja maalijoukko on {1, 3, 5, 7, 9}.
Esimerkki 2.
Mitkä seuraavista kuvaavat funktioita?
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
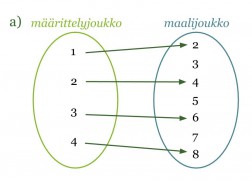
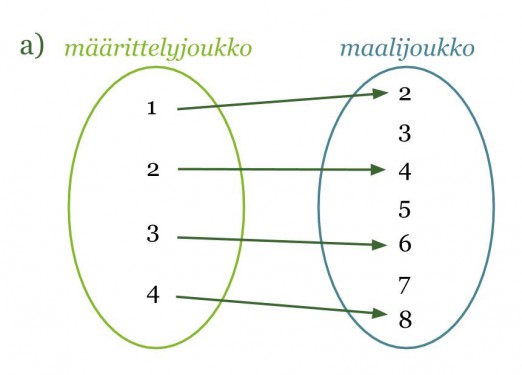
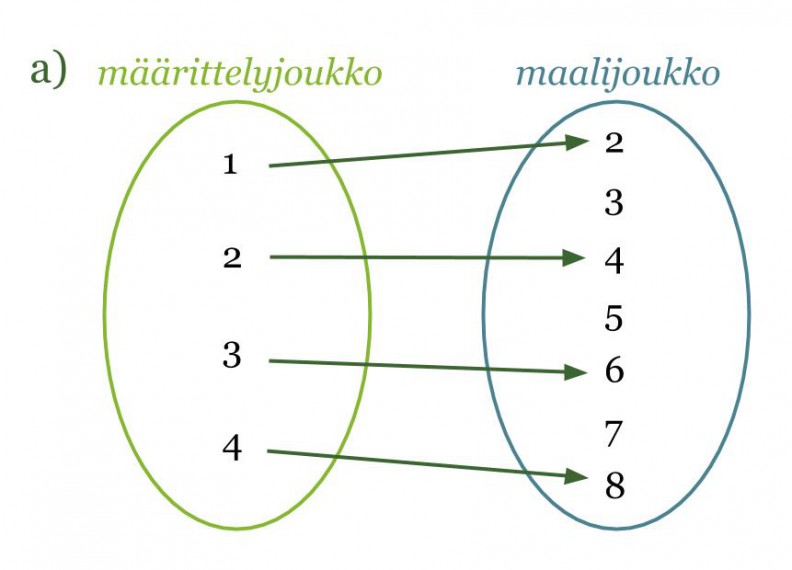
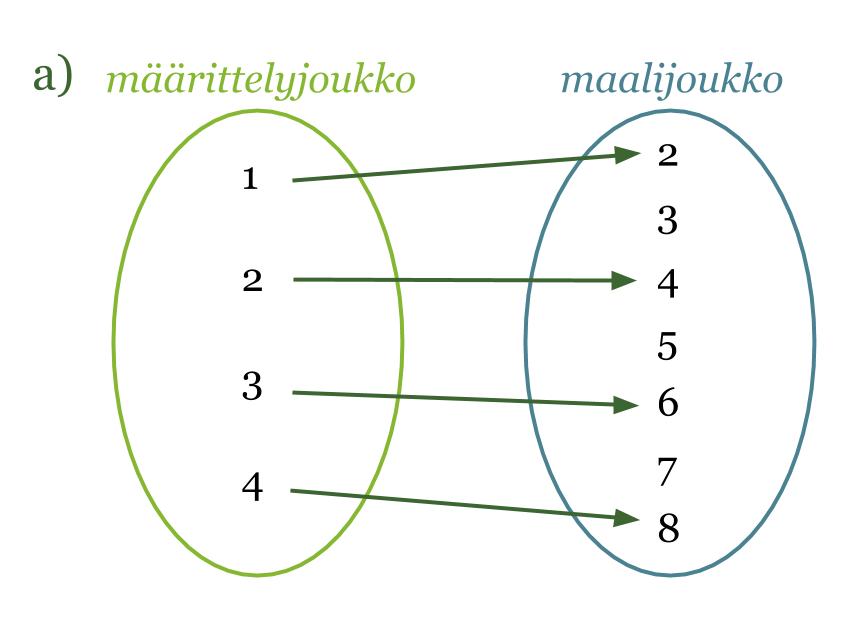
a) Kyseessä on funktio, sillä määrittelyjoukon jokaista lukua vastaa täsmälleen yksi maalijoukon luku. Arvojoukon luku on saatu kertomalla määrittelyjoukon luku kahdella.
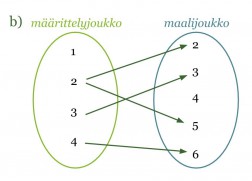
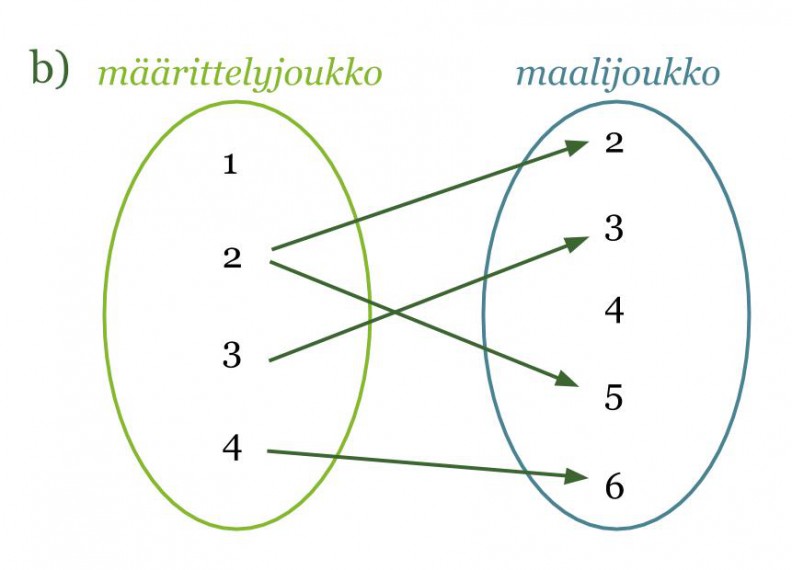
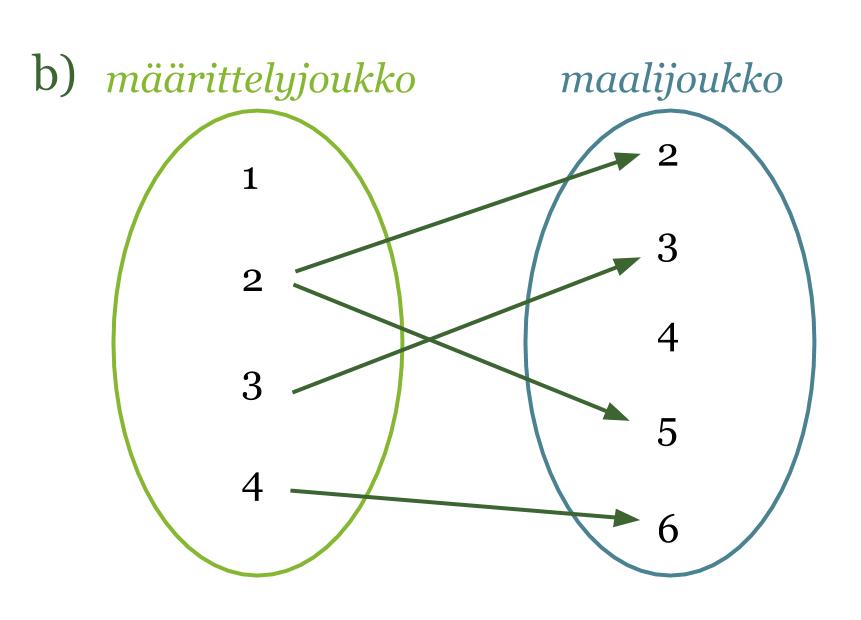
b) Kyseessä ei ole funktio. Määrittelyjoukon luku 2 kuvautuu kahdeksi eri arvoksi. Funktion on aina annettava arvo samojen sääntöjen mukaisesti. Lisäksi määrittelyjoukon luku 1 ei kuvaudu miksikään.
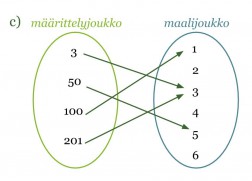
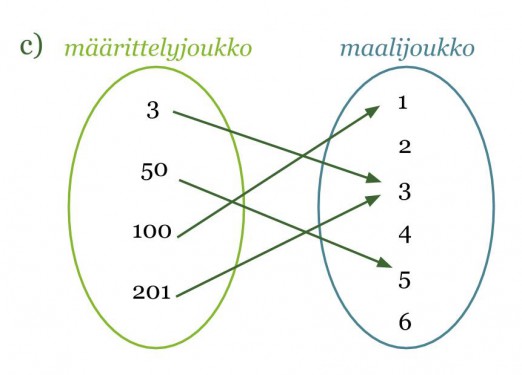
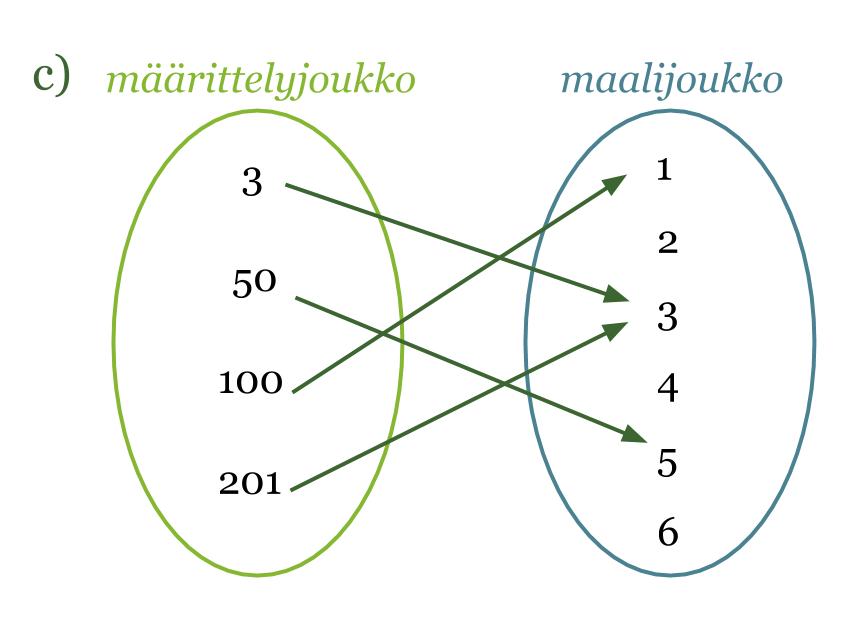
c) Kyseessä on funktio. Funktio kuvaa määrittelyjoukon luvut luvuiksi, jotka ovat arvojoukon lukujen numeroiden summa.
Huom! Määrittelyjoukon luku ei voi kuvautua kahdeksi eri maalijoukon luvuksi, mutta kaksi eri määrittelyjoukon lukua voivat kuvautua samaksi maalijoukon luvuksi.
Esimerkki 3.
Funktion f arvot lasketaan säännöllä ”Luvusta vähennetään yksi ja erotus kerrotaan luvulla 3”.
a) Muodostetaan funktion lauseke.
Merkitään lukua kirjaimella x, jolloin f(x) = (x – 1) · 3 = 3x – 3.
b) Lasketaan funktion arvo pisteessä 6.
Sijoitetaan nyt aiempaan funktioon x:n paikalle luku 6:
f(6) = 3 · 6 – 3 = 15
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014