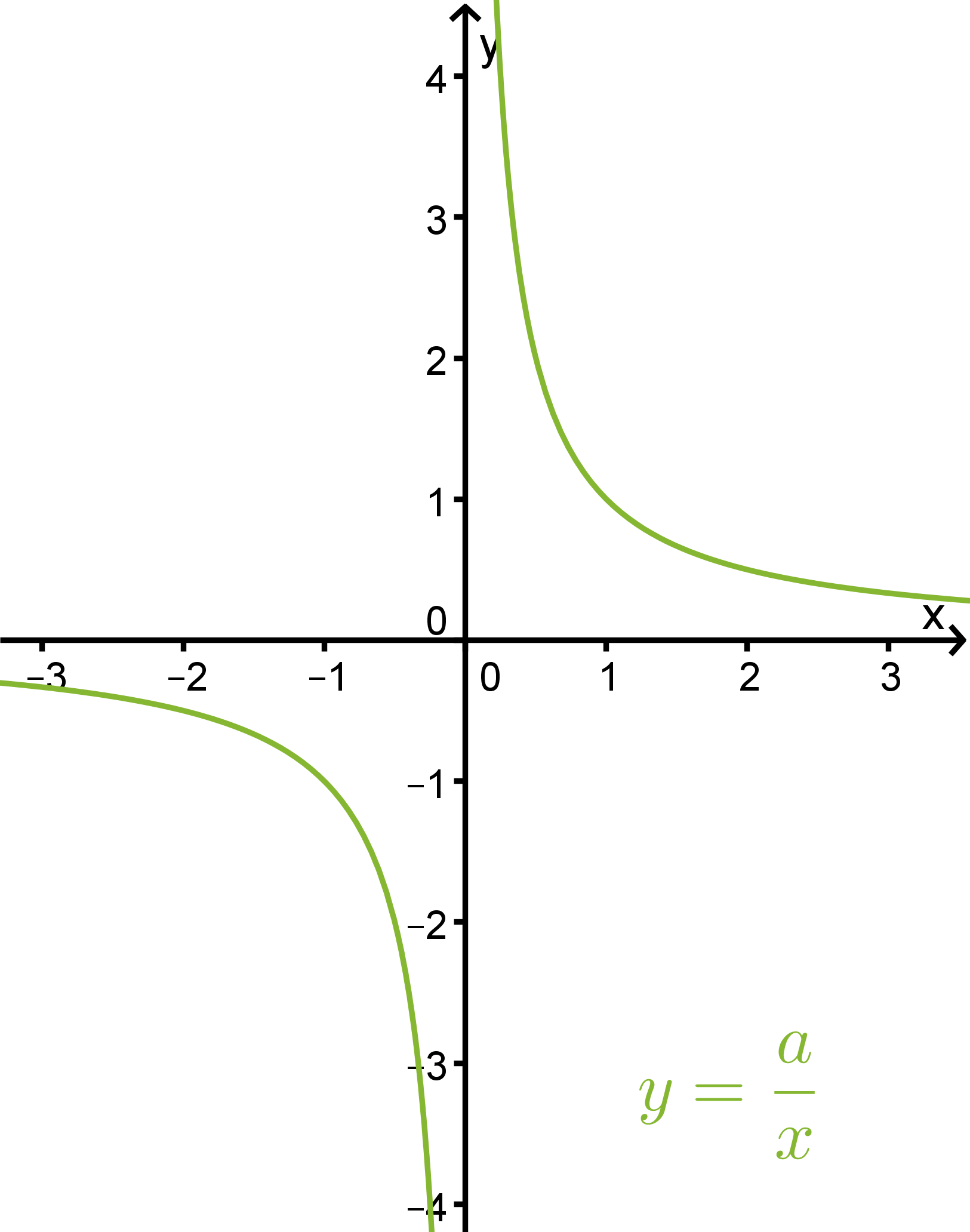
3. Funktion kuvaaja
Funktioita on kahta eri tyyppiä: kokemusperäisiä sekä matemaattisia funktioita. Kokemusperäinen funktio piirretään tehtyjen mittausten pohjalta. Esimerkiksi lämpötilaa ei voida piirtää ajan funktiona suorittamatta mittauksia.Lämpötila ja kellonaika ovat toinen toisistaan riippumattomia, eikä lämpötilaa siis voida laskea pelkän kellonajan perusteella.
Kun lukuparin pisteitä sitoo toisiinsa jokin matemaattinen yhtälö, voidaan lukuparin toinen piste laskea, kun toinen piste ja yhtälö tunnetaan. Mittauksiin ei tarvitse välttämättä ryhtyä, jos halutaan piirtää kuvaaja pallon tilavuudesta säteen funktiona. Hyväksi voidaan käyttää jo olemassa olevaa matemaattista yhtälöä. Säteen ja tilavuuden välinen riippuvuus on täsmällistä, pisteet sijoittuvat tarkasti tietylle käyrälle.
Usein on havainnollisempaa esittää funktiot graafisesti kuvaajana kuin pelkästään matemaattisena lausekkeena. Kuvaajan avulla voidaan määrittää funktion arvo myös sellaisissa pisteissä, joilla mittauksia ei ole suoritettu. Funktion kuvaajan muoto määräytyy sen asteluvun perusteella.
Funktion asteluvun ilmoittaa yhtälössä muuttujan korkein eksponentti.
Jos funktion kuvaaja on suora, on aina kyseessä ensimmäisen asteen polynomifunktio. Korkeamman asteen funktioiden kuvaajat ovat käyräviivaisia.Toisen asteen funktion kuvaajaan perehdytään kirjan kolmannessa osiossa.
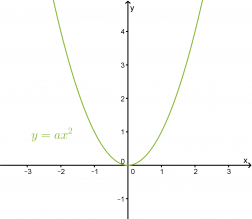
Toisen asteen funktio
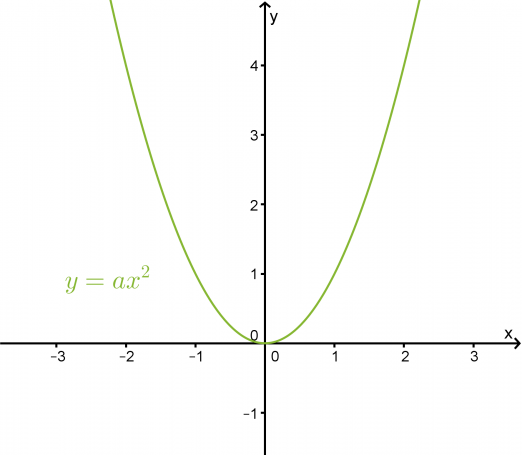
Toisen asteen funktio
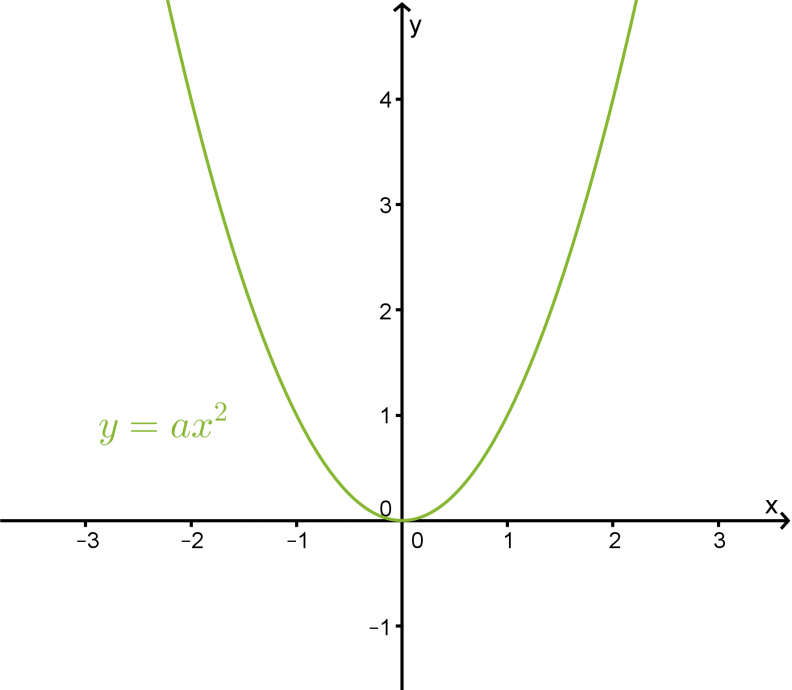
Toisen asteen funktio
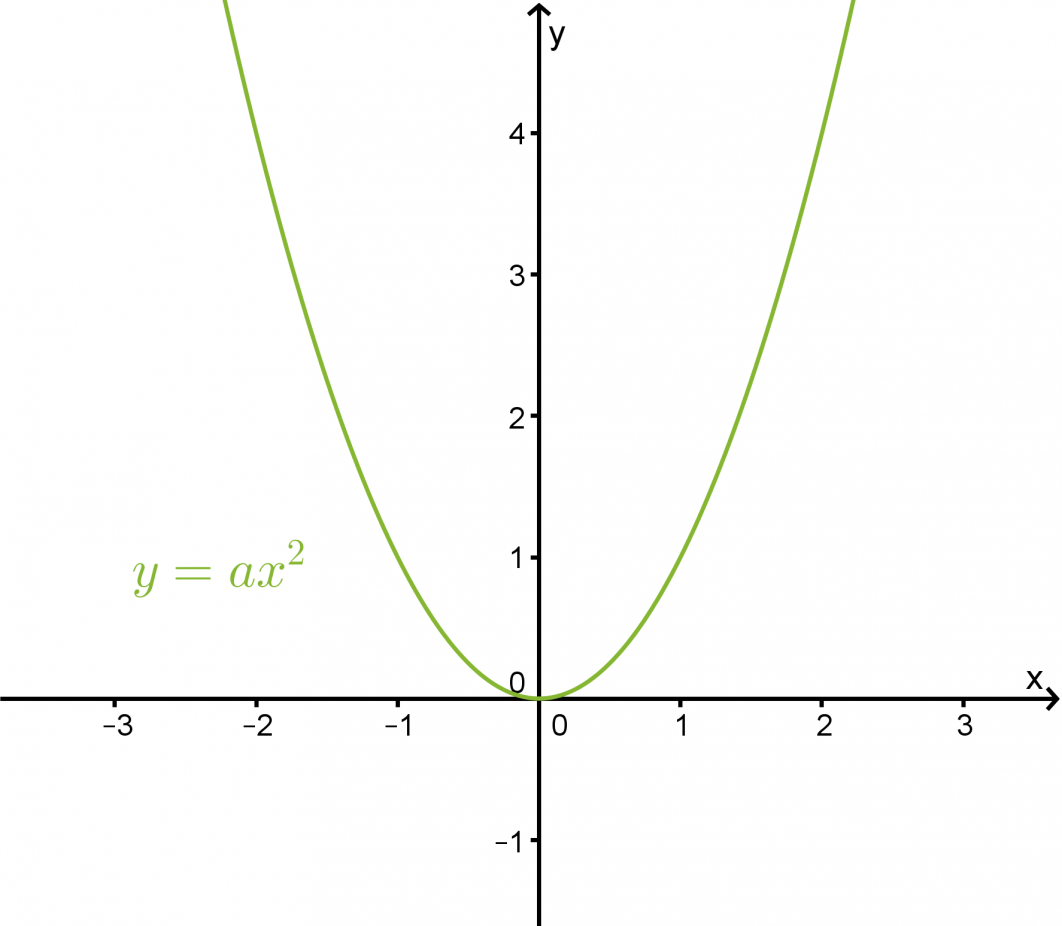
Toisen asteen funktio
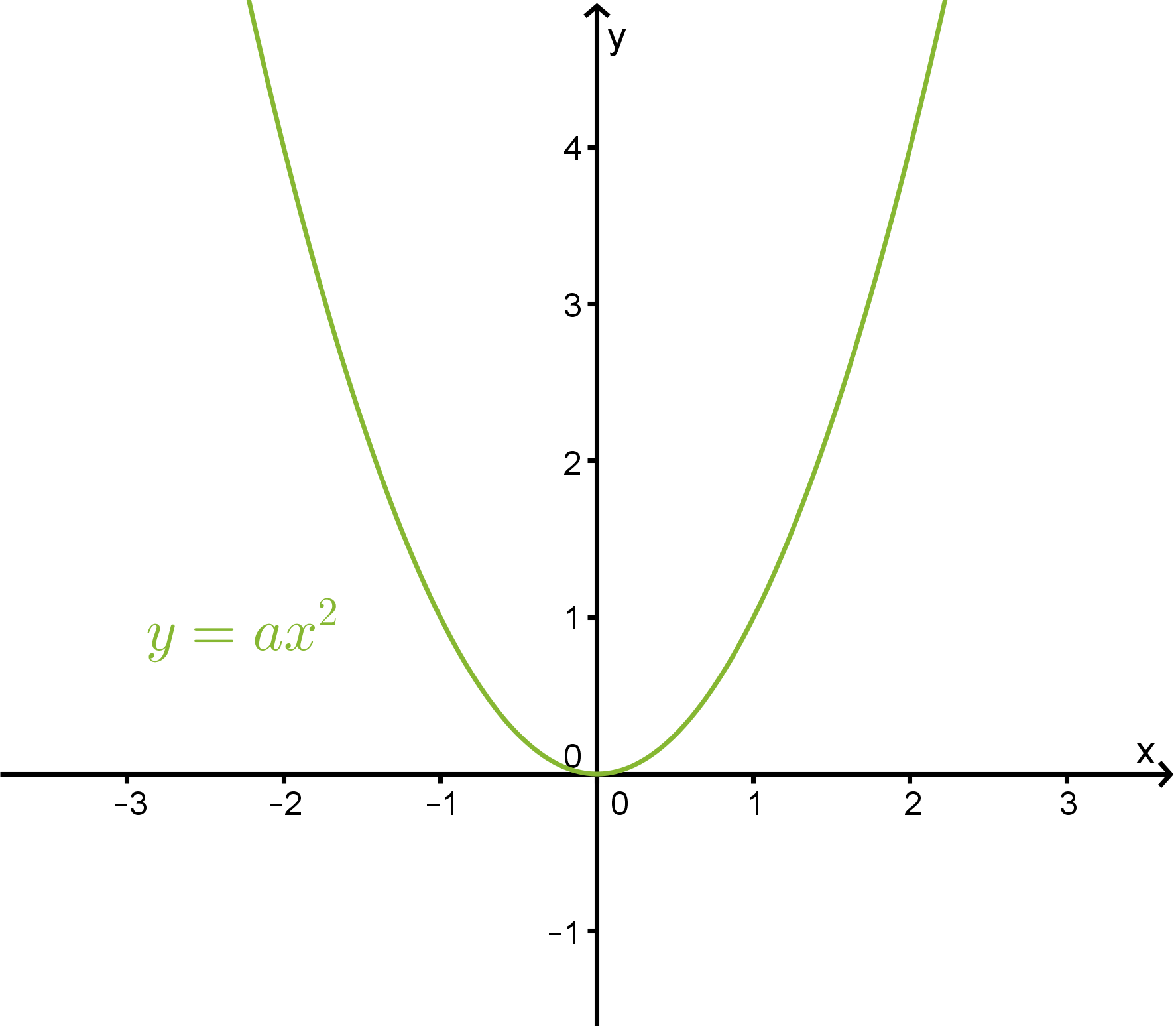
Toisen asteen funktio

Toisen asteen funktio
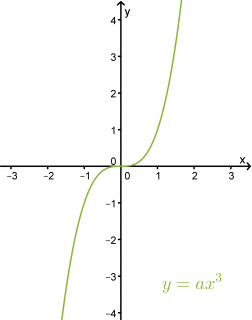
Kolmannen asteen funktio
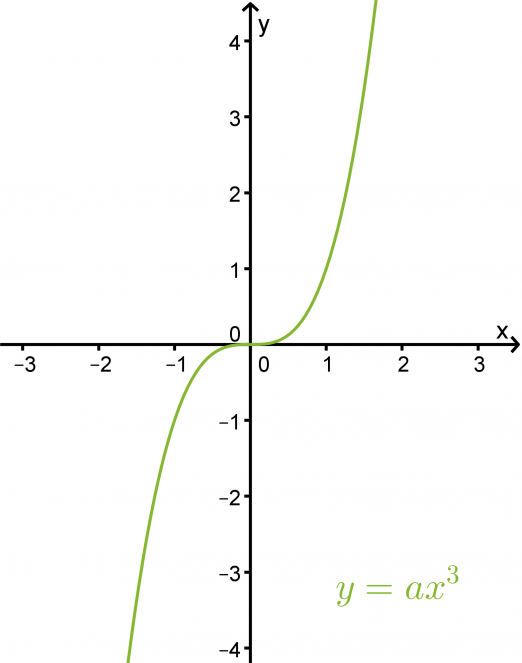
Kolmannen asteen funktio
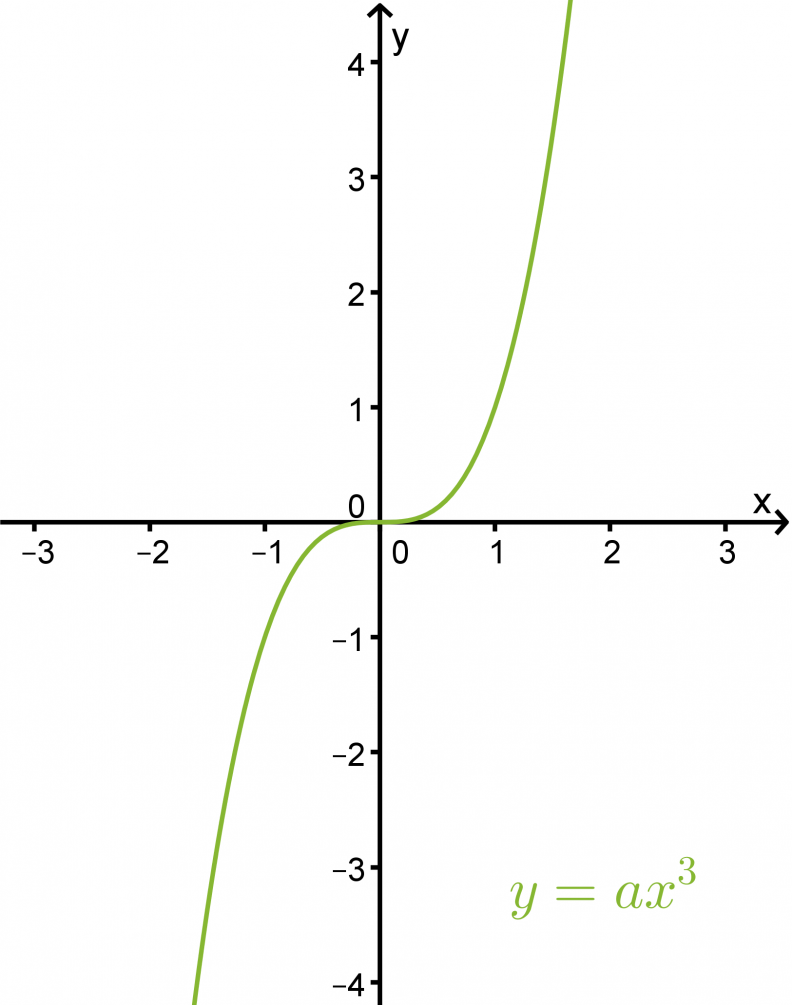
Kolmannen asteen funktio
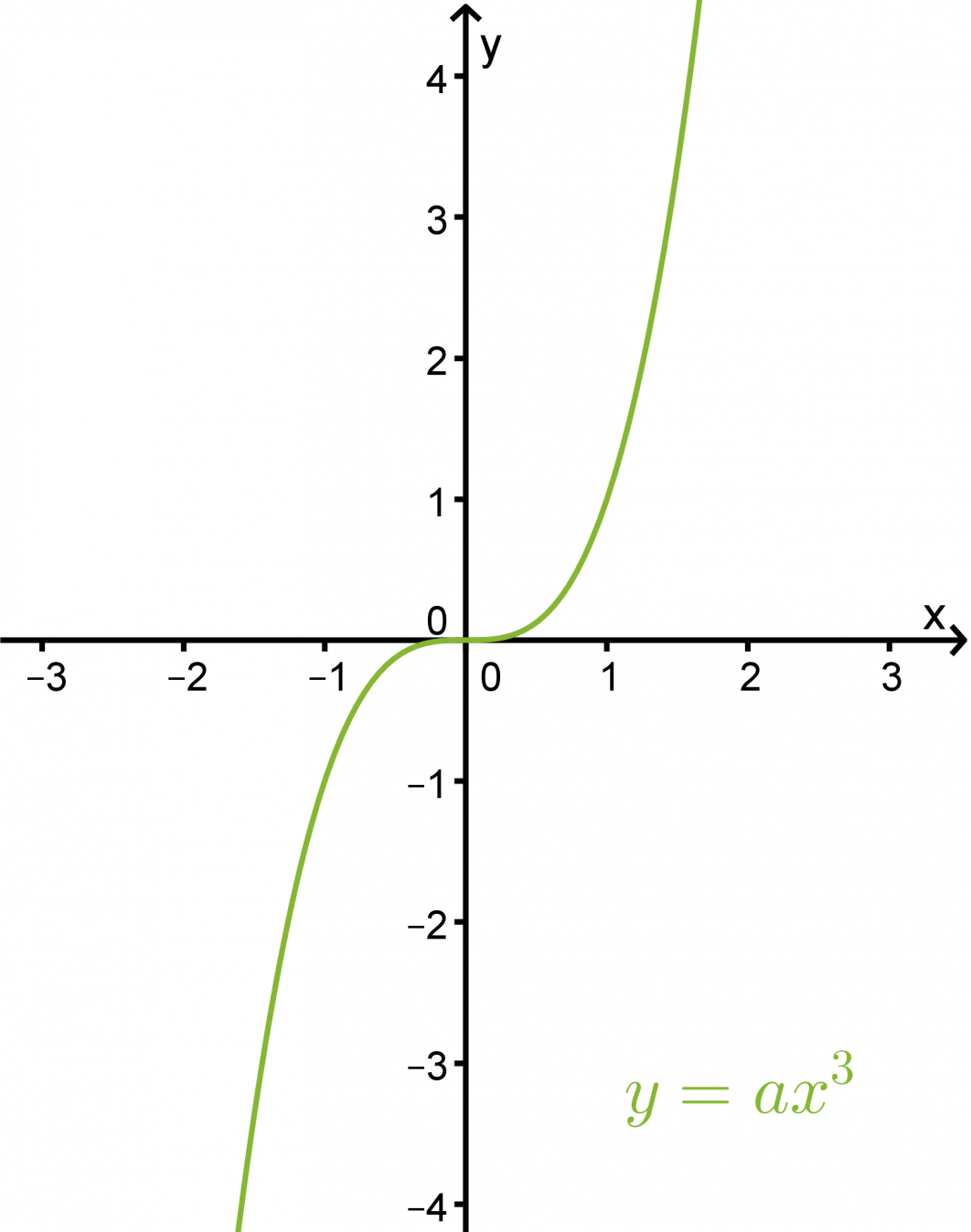
Kolmannen asteen funktio
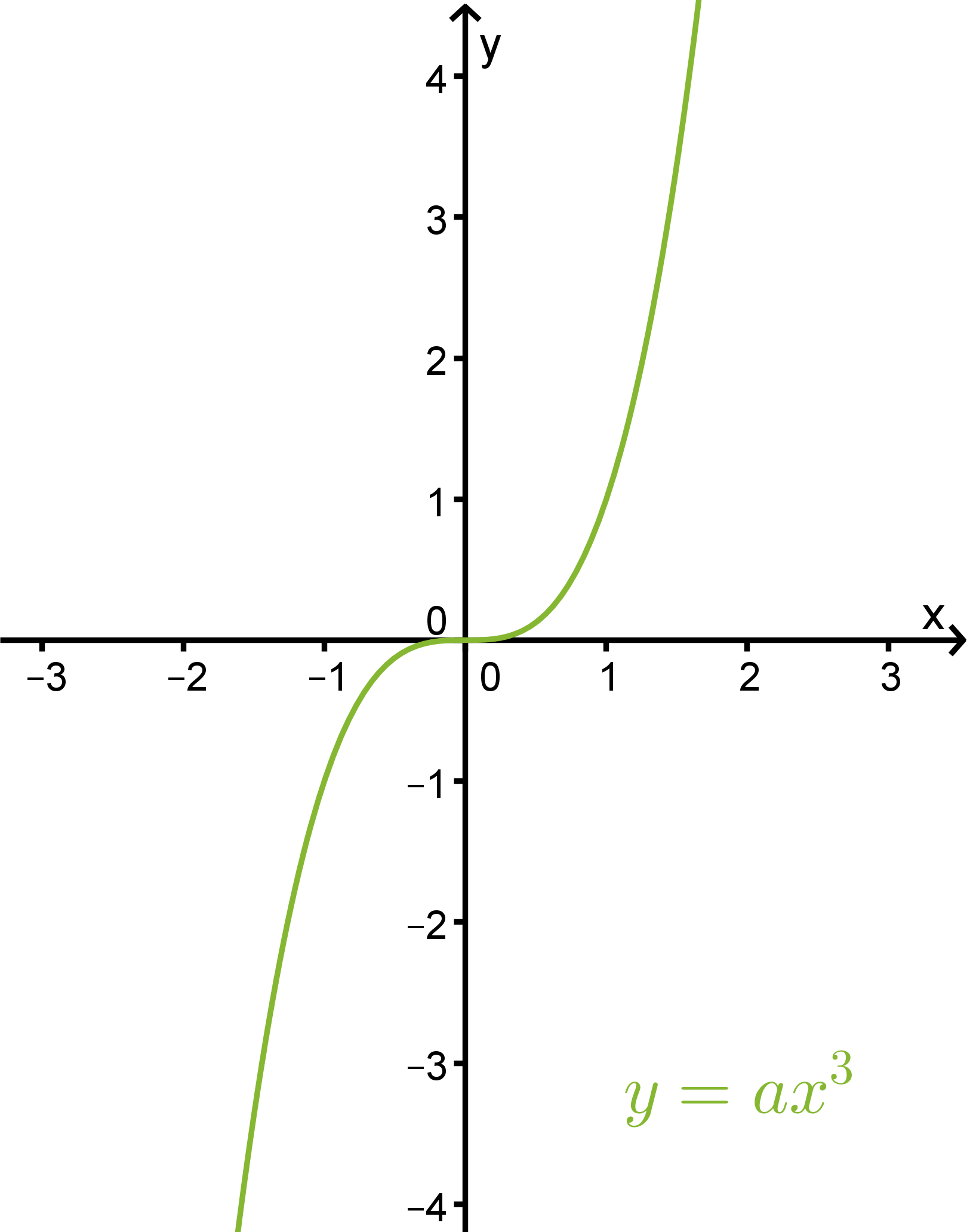
Kolmannen asteen funktio

Kolmannen asteen funktio
Esimerkki 1.
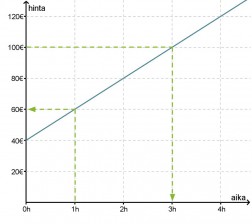
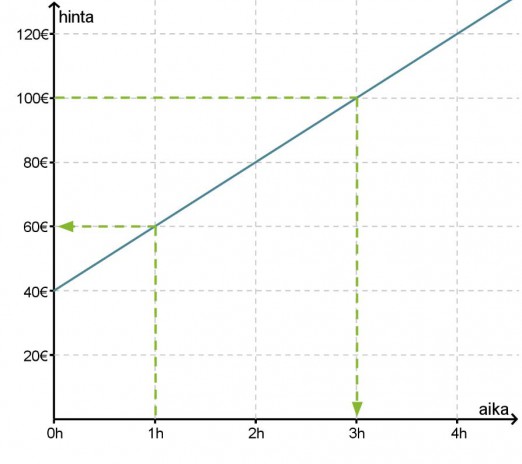
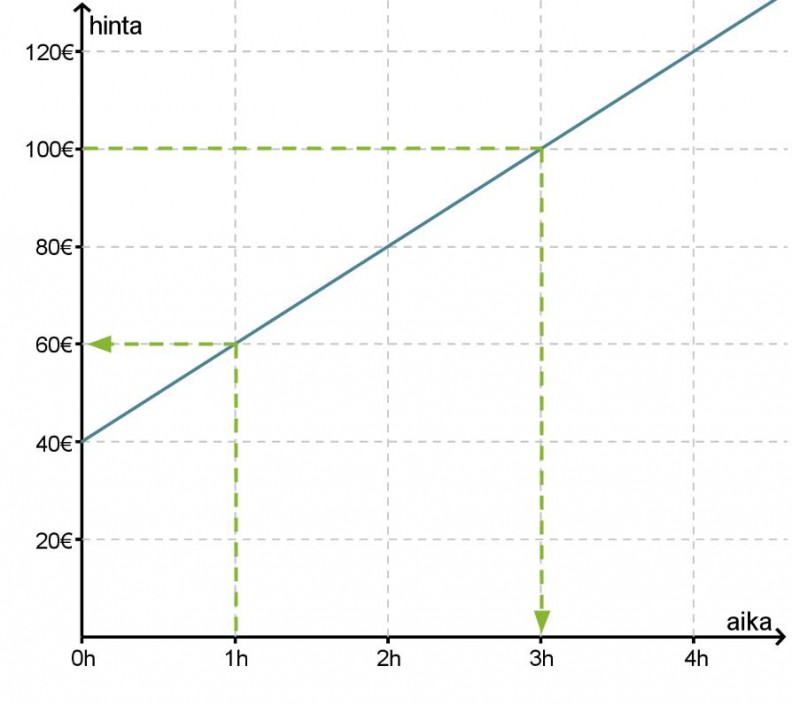
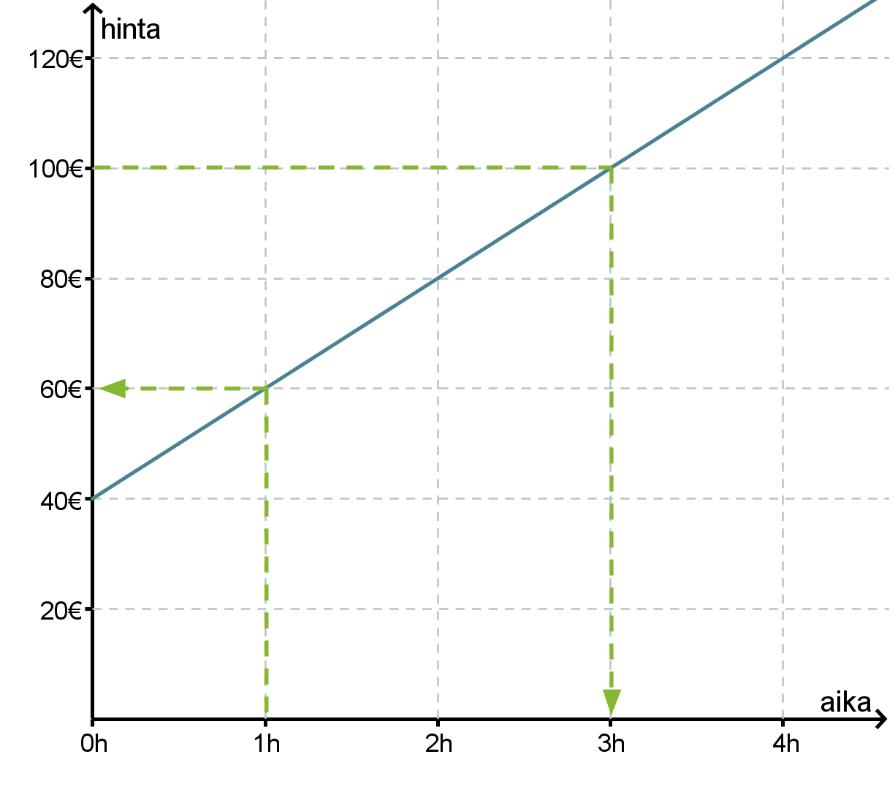
Autokorjaamo velottaa asiakkaitaan seuraavasti: varaosien hinnat maksetaan sellaisenaan ja itse korjauksesta maksetaan siihen kuluneen ajan mukaan. Työn hinta on siis ajan funktio, mikä esitetään kuvaajan avulla.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kuvaajasta voidaan lukea arvoja molempiin suuntiin:
- Jos työhön käytettävä aika on 1 h, on työn hinta 60 €. Eli muuttujan arvolla 1 h funktio saa arvon 60 €.
- Jos työstä maksetaan 100 €, niin työhön on käytetty aikaa 3 h. Eli funktio saa arvon 100 € muuttujan arvolla 3 h.
Kaikkia arvoja kuvaajasta ei kuitenkaan pystytä lukemaan. Esimerkiksi viiden tunnin korjauksen hintaa ei nähdä välittömästi. Kuvaajana olevaa suoraa jatkamalla voidaan kustannukset määrittää myös pidemmille korjausajoille. Toinen vaihtoehto on muodostaa kuvaajan perusteella funktion lauseke, jolla saadaan lasketuksi kustannukset minkä pituiselle korjausajalle tahansa. Tähän perehdytään seuraavassa kappaleessa.

Murtofunktio (x nimittäjässä)