4. Nollannen ja ensimmäisen asteen polynomifunktio
Esimerkiksi funktio f(x) = x + 3 on ensimmäisen asteen polynomifunktio, jonka kuvaaja on suora y = x + 3. Vieläkö muistat, miten suora piirretään hyödyntämällä suoran yhtälön ratkaistua muotoa?
Suoran yhtälön ratkaistu muoto on
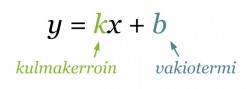
Klikkaa kuva suuremmaksi!
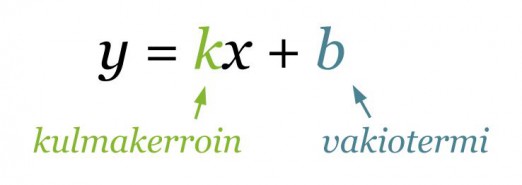
Klikkaa kuva suuremmaksi!
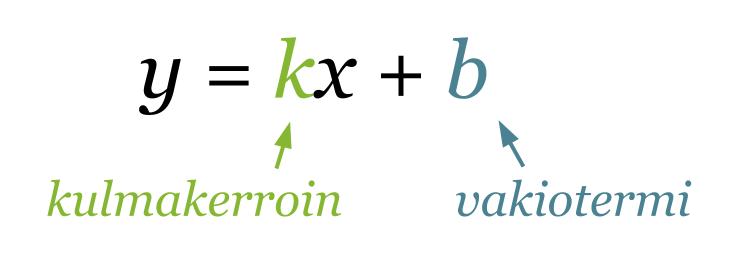
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
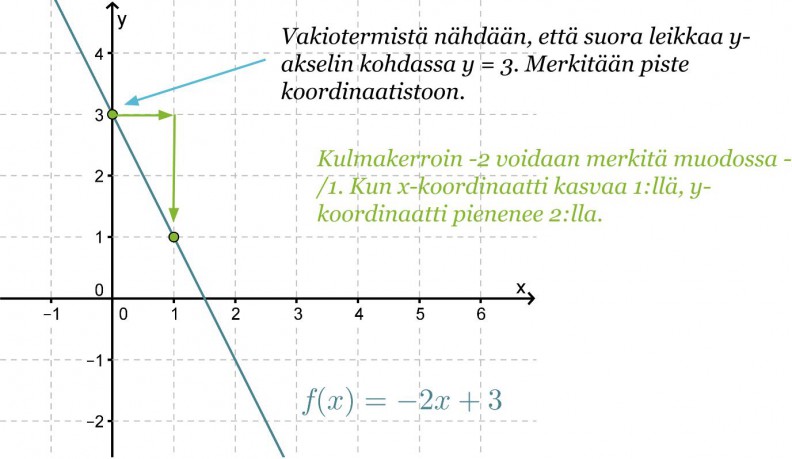
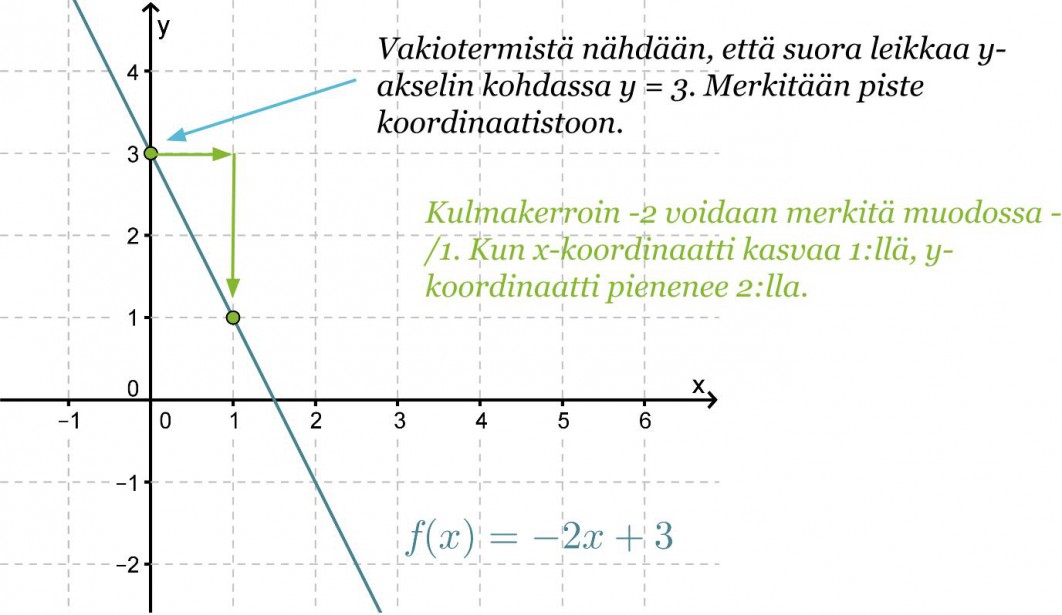
Vakiotermi b kertoo kohdan, jossa suora leikkaa y-akselin. Se on suoran kuvaajan ja y-akselin leikkauspisteen y-koordinaatti. Toinen piste, jonka kautta suora kulkee, määritetään kulmakertoimesta. Suoran kulmakerroin kertoo paljonko y-koordinaatti muuttuu (kasvaa tai vähenee), kun x-koordinaatti kasvaa yhdellä. Siirrytään koordinaatistossa y-akselin leikkauspisteestä kulmakertoimen nimittäjän ilmoittama määrä x-akselin suuntaisesti ja osoittajan ilmoittama määrä y-akselin suuntaisesti.
Vastaavasti suoran kuvaajan perusteella voidaan määrittää suoran yhtälö ja edelleen mitä funktiota se kuvaa. Suoran yhtälön y = kx + b vakiotermi nähdään kuvaajan ja y-akselin leikkauspisteestä. Kulmakerroin voidaan puolestaan laskea kahden suoralla olevan pisteen avulla. Sen arvo on riippumaton suoralla olevien pisteiden valinnasta.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ensimmäisen asteen polynomifunktion kuvaaja on aina nouseva tai laskeva suora.Funktion kasvaminen ja väheneminen on sitä voimakkaampaa mitä suurempi itseisarvo kulmakertoimella on.
Jos kulmakerroin
- k > 0, on funktio kasvava
- k < 0, on funktio vähenevä
- k = 0, on funktio vakiofunktio
Jos kulmakerroin on nolla, häviää funktion yhtälöstä x kokonaan, eikä funktion arvo siis riipu mitenkään muuttujan x arvosta. Tällaista funktiota kutsutaan nollannen asteen polynomifunktioksi eli vakiofunktioksi. Nollannen asteen polynomifunktion kuvaaja on x-akselin suuntainen suora y = t, missä t on suoran ja y-akselin leikkauspisteen y-koordinaatti.
Miksi y-akselin suuntainen suora ei ole minkään funktion kuvaaja?
Esimerkki 1.
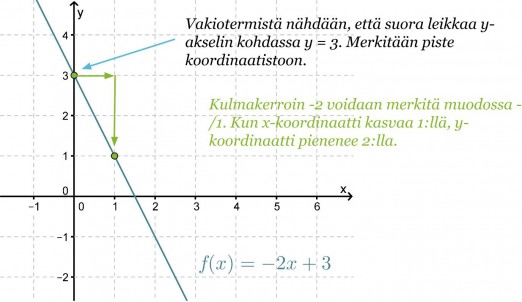
Piirretään funktion f(x) = –2x + 3 kuvaaja.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Muodostetaan autokorjaamon työstä perittävän hinnan funktio käytetyn ajan suhteen ja lasketaan funktion avulla paljonko maksaa viiden tunnin työ.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
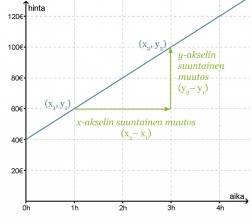
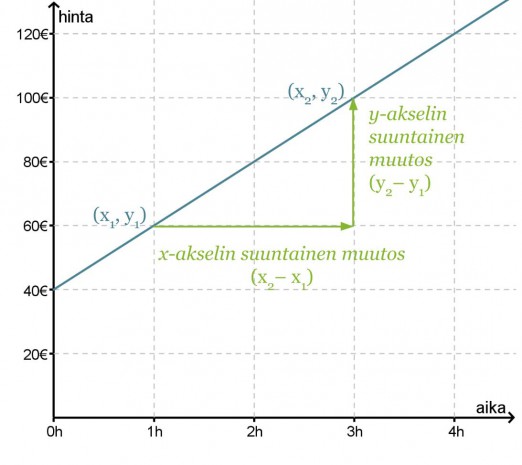
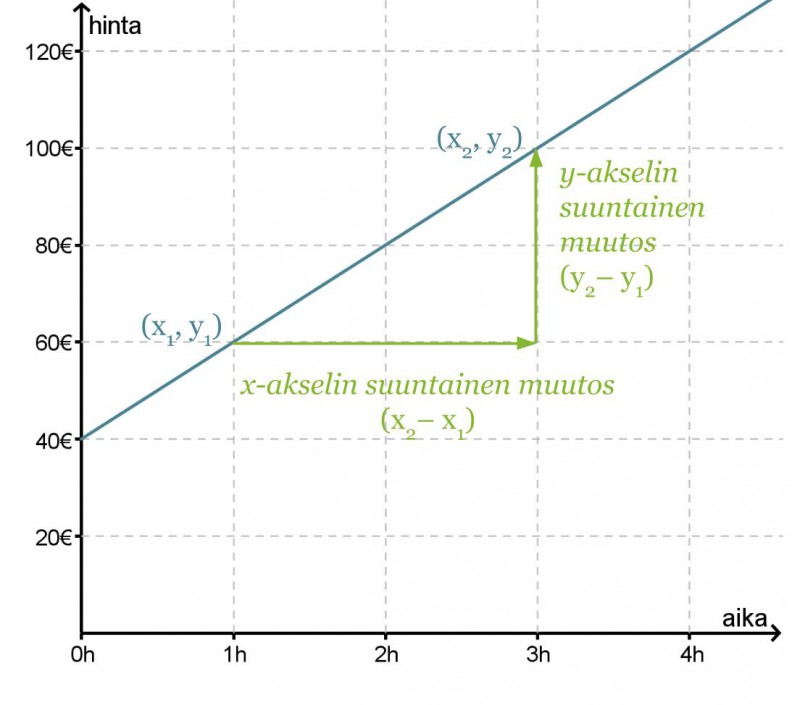
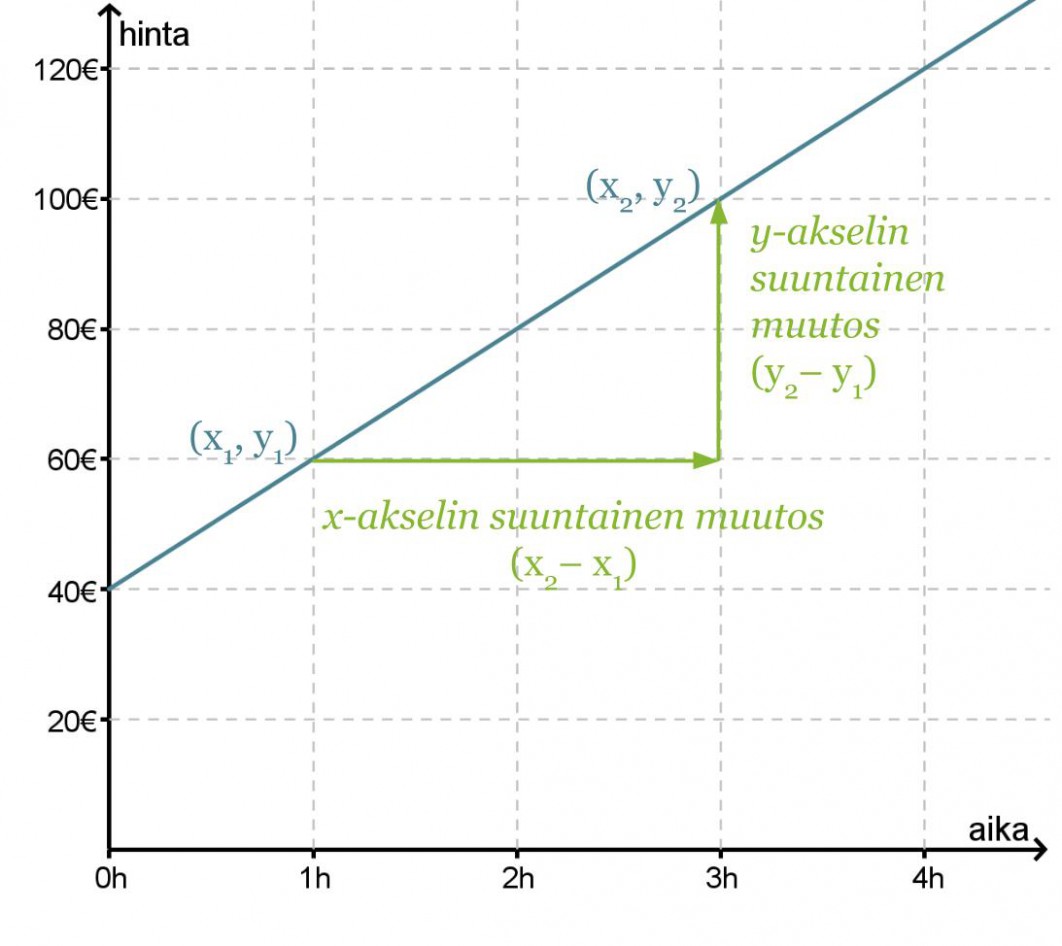
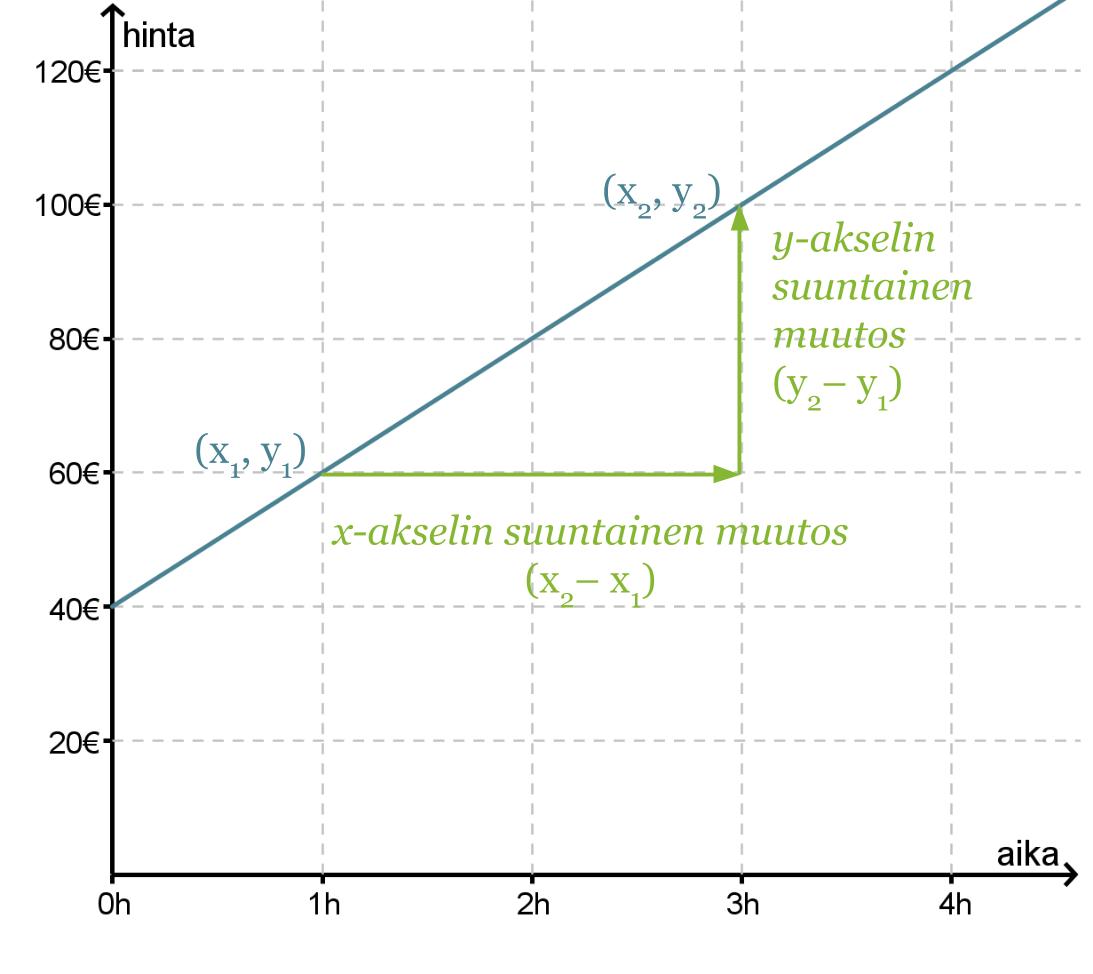
Merkitään aikaa x:llä ja hintaa y:llä. Suoran yhtälö on muotoa y = kx + b. Jotta saisimme kuvaajaa vastaavan yhtälön muodostettua, on ratkaistava ja sijoitettava suoran yhtälöön kulmakerroin ja vakiotermi.
Vakiotermi b saadaan suoran ja y-akselin leikkauspisteestä eli b = 40.
Valitaan tarkastelupisteiksi (x1, y1) = (1, 60) ja (x2, y2) = (3, 100), joiden avulla lasketaan kulmakerroin.
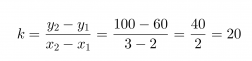
Klikkaa kuva suuremmaksi!
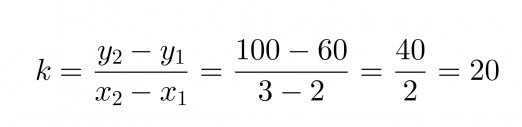
Klikkaa kuva suuremmaksi!
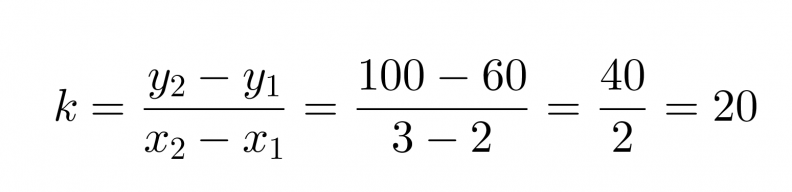
Klikkaa kuva suuremmaksi!
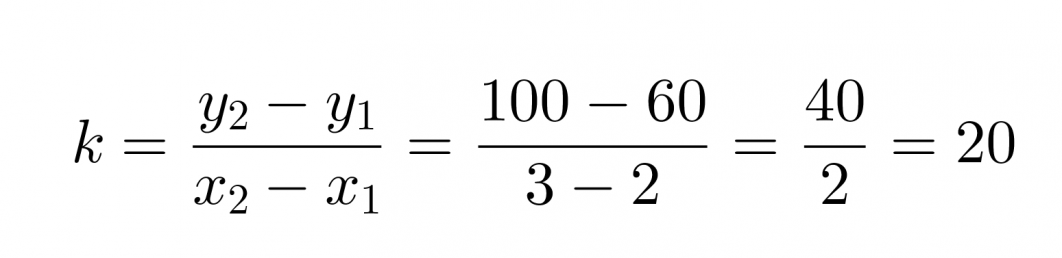
Klikkaa kuva suuremmaksi!
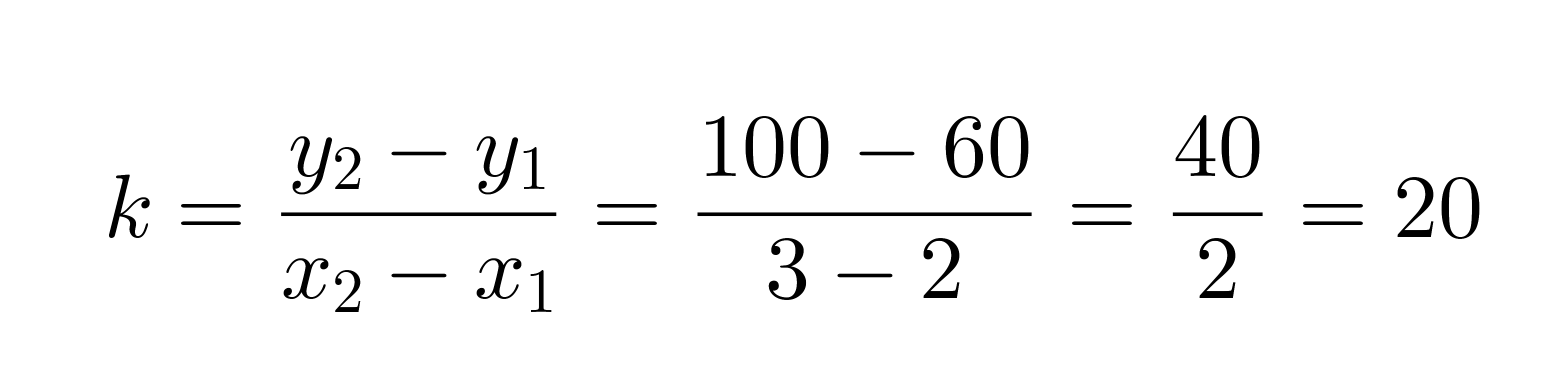
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Sijoitetaan kulmakerroin ja vakiotermi suoran yhtälöön, jolloin saadaan y = 20x + 40 eli hintafunktio on f(x) = 20x + 40.
Funktion arvoksi saadaan x:n arvolla 5 f(5) = 20 · 5 + 40 = 140.
Vastaus: Hinta saadaan määritetyksi funktiosta f(x) = 20x + 40 , missä x on työskentelyaika tunteina. Viiden tunnin työn hinta 140 €.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014
Kulmakertoimen laskeminen