5. Funktion nollakohta ja lineaarinen riippuvuus
Millä x:n arvolla funktio saa arvon nolla tai missä pisteessä funktion kuvaaja leikkaa x-akselin? Kyse on samasta asiasta, funktion nollakohdan määrittämisestä. Likimääräisesti nollakohta voidaan määrittää piirtämällä. Se on myös helposti laskettavissa.
Funktion f nollakohdalla tarkoitetaan sitä x:n arvoa, joka toteuttaa ehdon f(x)= 0.
Funktion nollakohta määritetään siis merkitsemällä funktion lauseke yhtä suureksi kuin nolla ja ratkaisemalla tämä yhtälö.
Jos funktion kuvaaja on suora, sanotaan suureiden x ja y riippuvan lineaarisesti toisistaan.Lineaarinen riippuvuus kuvaa tasaista muutosta eli muutos yksikköä kohden on joka vaiheessa yhtä suuri. Positiivinen muutos tarkoittaa lineaarista kasvamista ja negatiivinen muutos tarkoittaa lineaarista vähenemistä. Jos tiedetään, että jokin ilmiö noudattaa lineaarista mallia ja tunnetaan kaksi tarkastelupistettä, voidaan tietojen pohjalta muodostaa mallin yhtälö.
Esimerkki 1.
Ratkaise funktion f(x) = x + 3 nollakohta
a) piirtämällä
b) laskemalla.
Ratkaisu:
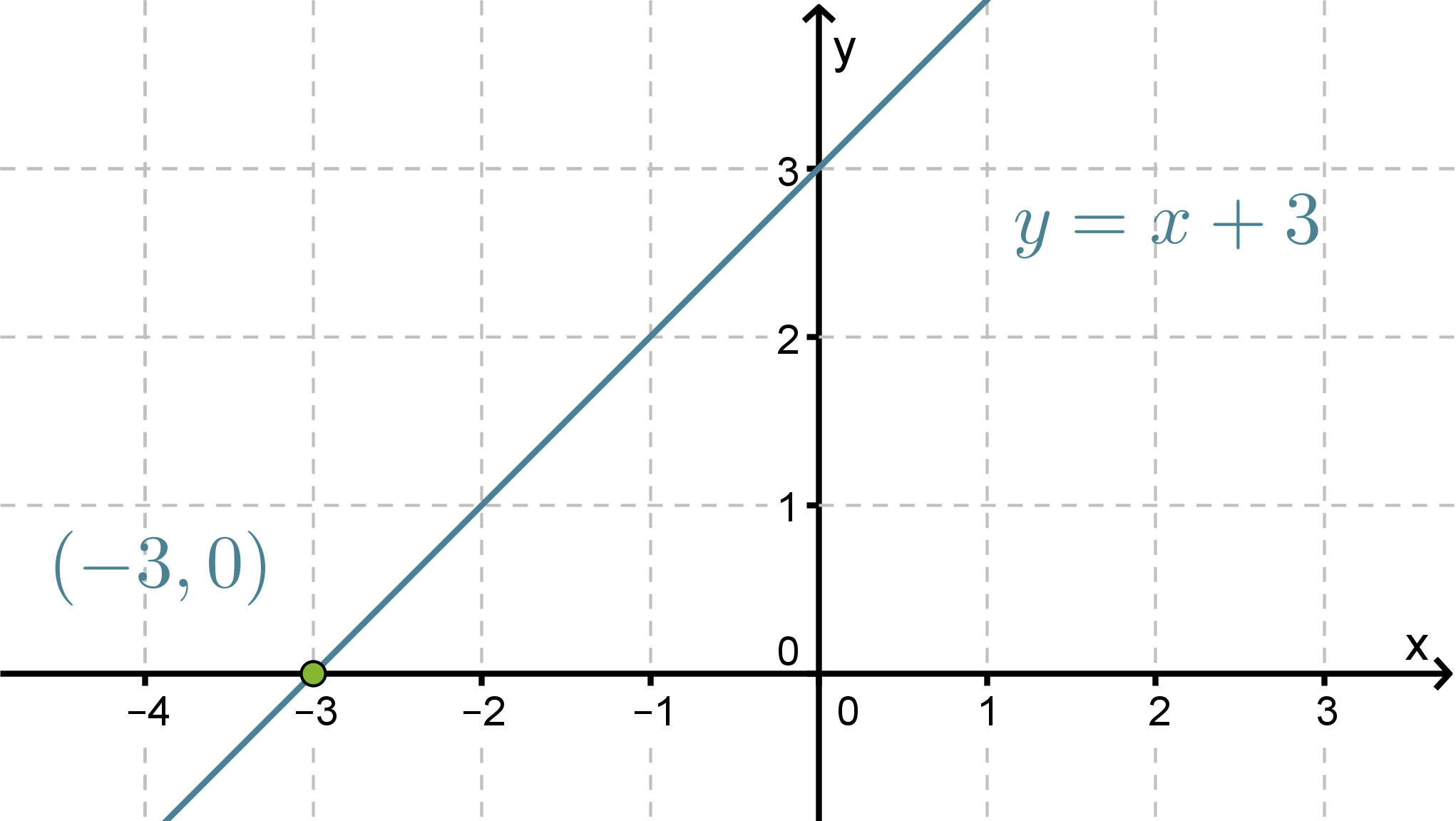
a) f(x) = x + 3 on ensimmäisen asteen polynomifunktio, jonka kuvaaja on suora y = x + 3. Piirretään tämä koordinaatistoon.
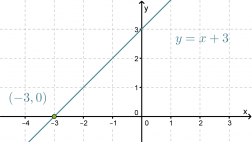
Klikkaa kuva suuremmaksi!
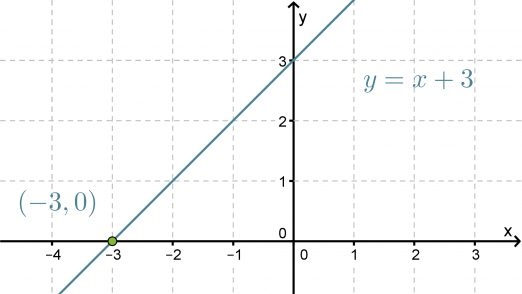
Klikkaa kuva suuremmaksi!
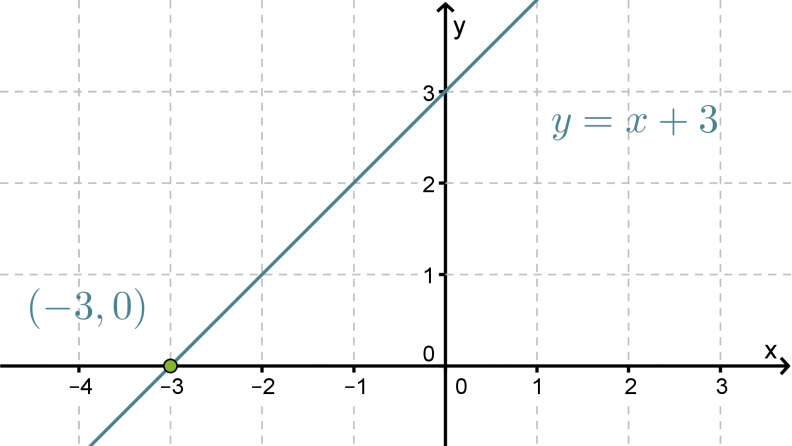
Klikkaa kuva suuremmaksi!
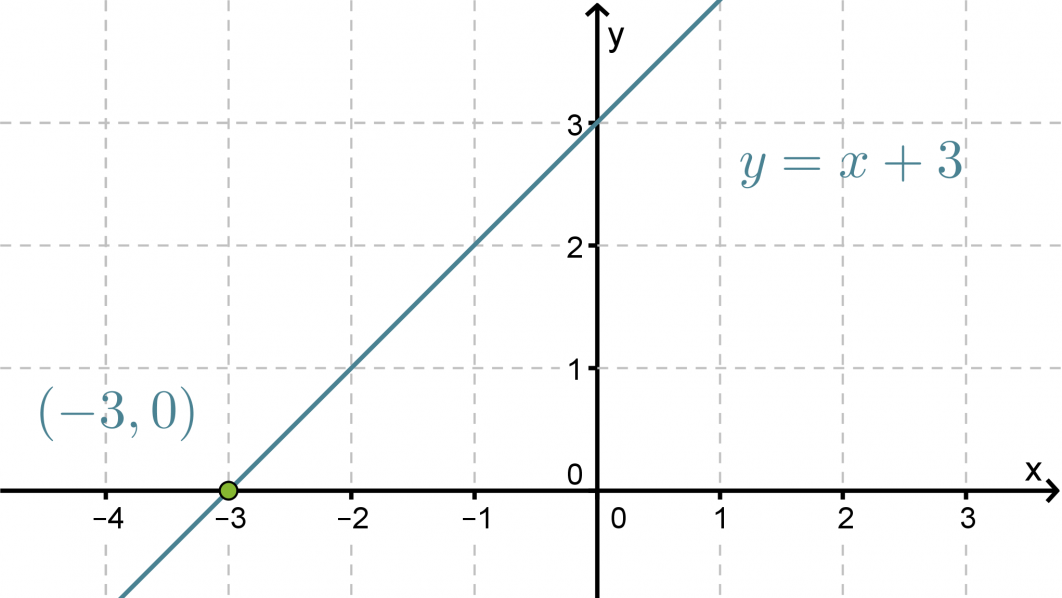
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Nollakohta löytyy funktion kuvaajan ja x-akselin leikkauspisteestä, joten se on x = -3.
b) Funktion nollakohta toteuttaa ehdon f(x) = 0, joten ratkaistaan yhtälö
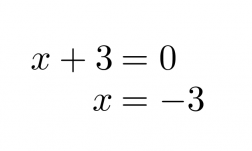
Klikkaa kuva suuremmaksi!
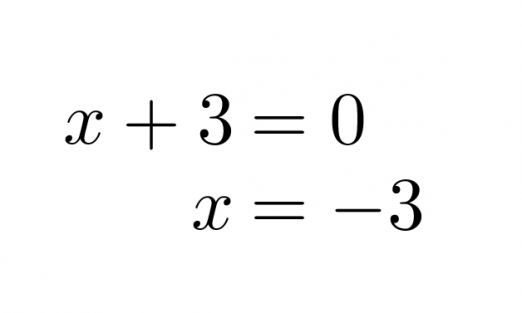
Klikkaa kuva suuremmaksi!
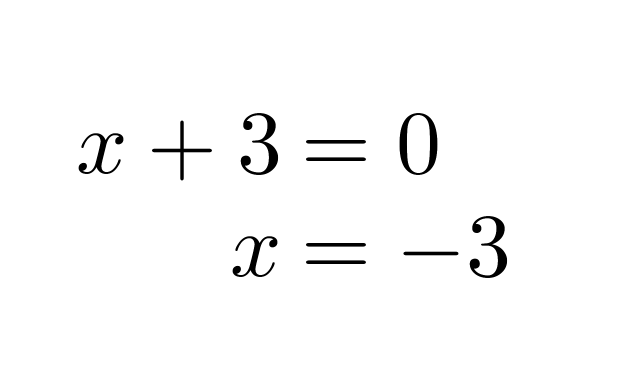
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: x = −3
Esimerkki 2.
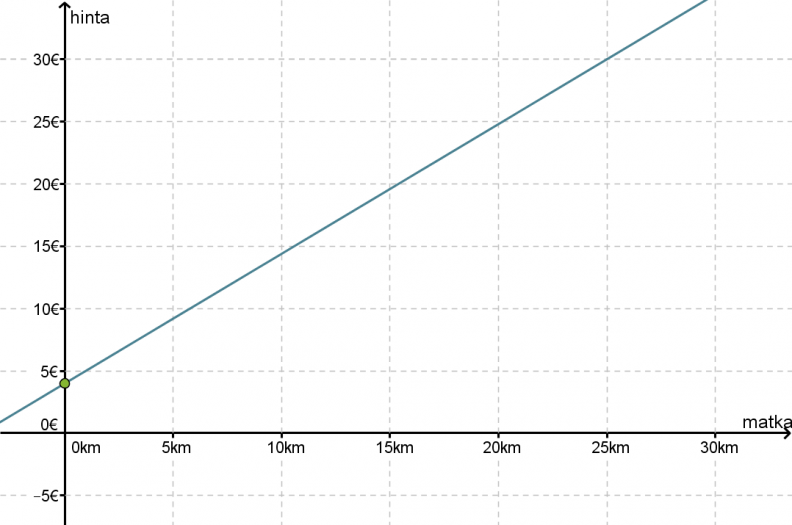
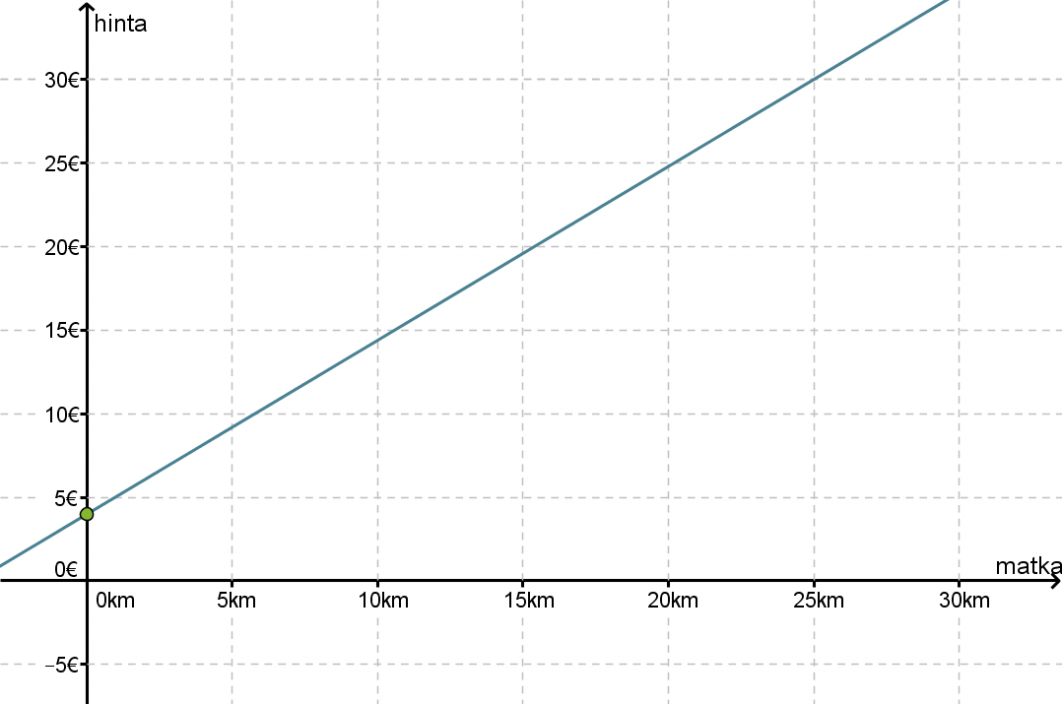
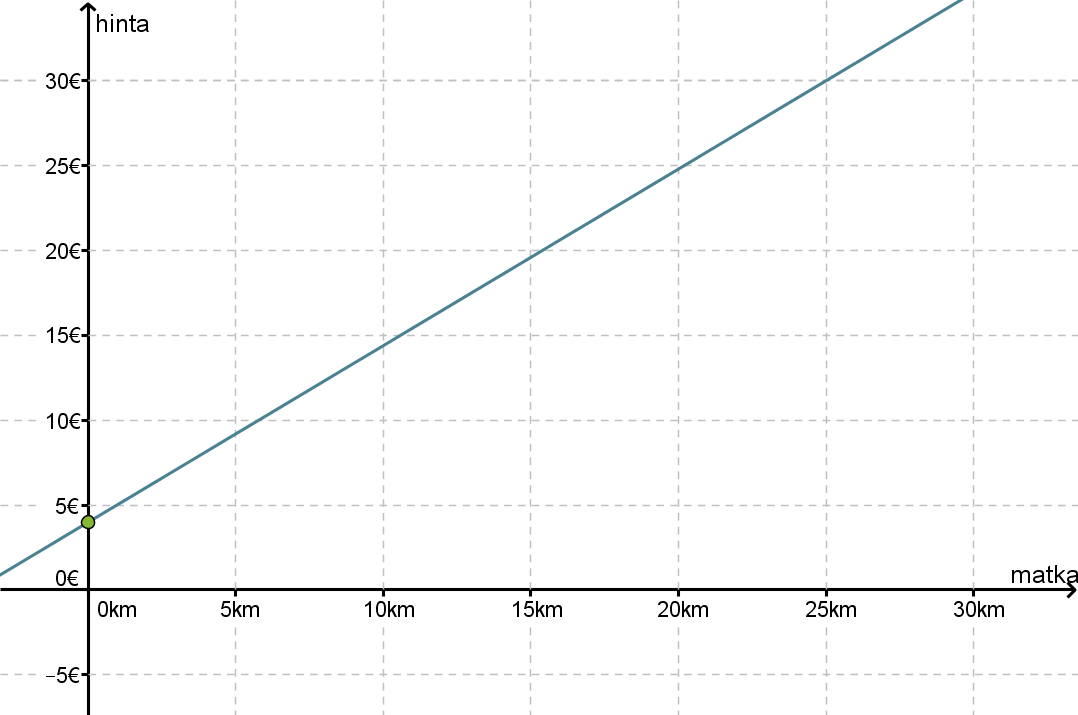
Taksin perusmaksu on 4 € ja jokainen kilometri maksaa 1,02 €/km. Muodosta funktio, joka ilmoittaa taksimatkan kustannukset matkan funktiona ja piirrä kuvaaja. Minkälainen riippuvuus on taksimatkan pituuden ja hinnan välillä?
Ratkaisu:
Merkitään taksimatkan pituutta x:llä (yksikkönä km), tällöin hintafunktioksi saadaan

Klikkaa kuva suuremmaksi!
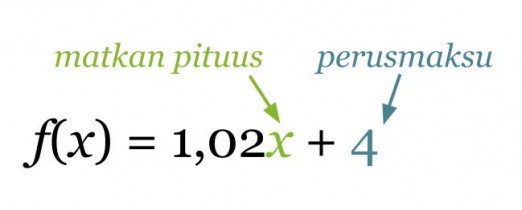
Klikkaa kuva suuremmaksi!
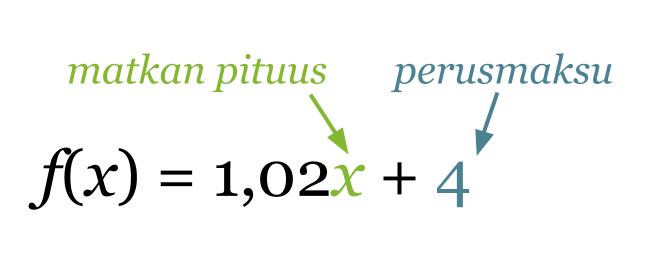
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
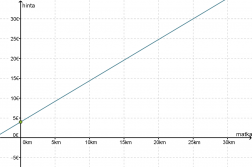
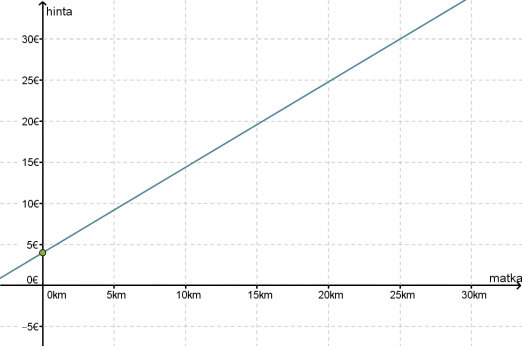
Funktio on ensimmäisen asteen polynomifunktio ja sen kuvaaja on suora.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Koska funktion kuvaaja on suora, joka ei kulje origon kautta, vallitsee taksimatkan pituuden ja hinnan välillä lineaarinen riippuvuus. Tämä olisi voitu päätellä myös suoraan funktion yhtälöstä kuvaajaa piirtämättä.
Funktion f(x) = 1,02x + 4 asteluku on yksi. Ensimmäisen asteen polynomifunktion kuvaaja on aina suora. Näin ollen taksimatkan pituuden ja hinnan välillä vallitsee lineaarinen riippuvuus.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014