6. Paloittain määritelty funktio*
Monissa tapauksissa funktio saa arvoja eri säännön mukaisesti eri muuttujan arvoilla. Esimerkiksi ostoksista voi saada paljousalennusta ja mitä enemmän tienaa sitä korkeammaksi veroprosentti nousee. Laskutavan muutos on selvästi havaittavissa funktion kuvaajasta, joka näyttää muodostuvan useasta eri palasta. Kyseessä onkin paloittain määritelty funktio. Paloittain määritelty funktio on jatkuva, jos sen kuvaaja on katkeamaton käyrä, muussa tapauksessa funktiota sanotaan epäjatkuvaksi.
Esimerkki 1.
Taulukossa on esitetty postimaksun riippuvuus kotimaahan lähetettävän kirjeen painosta.
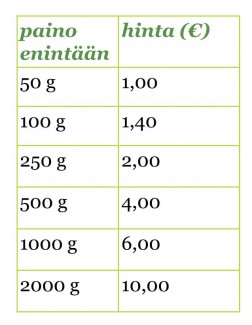
Klikkaa kuva suuremmaksi!
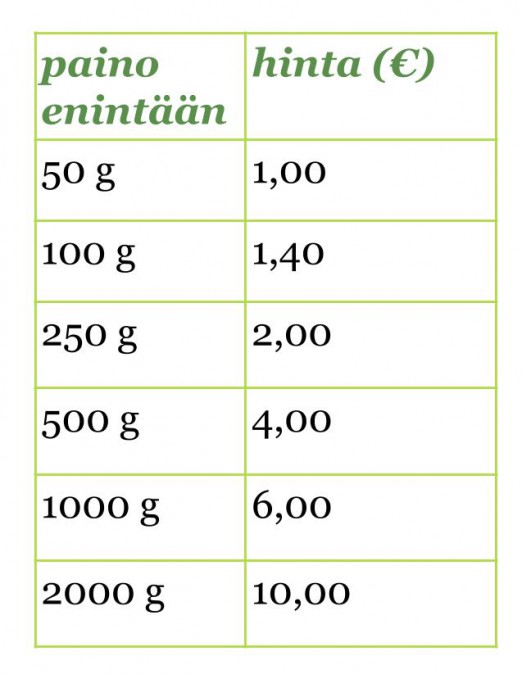
Klikkaa kuva suuremmaksi!
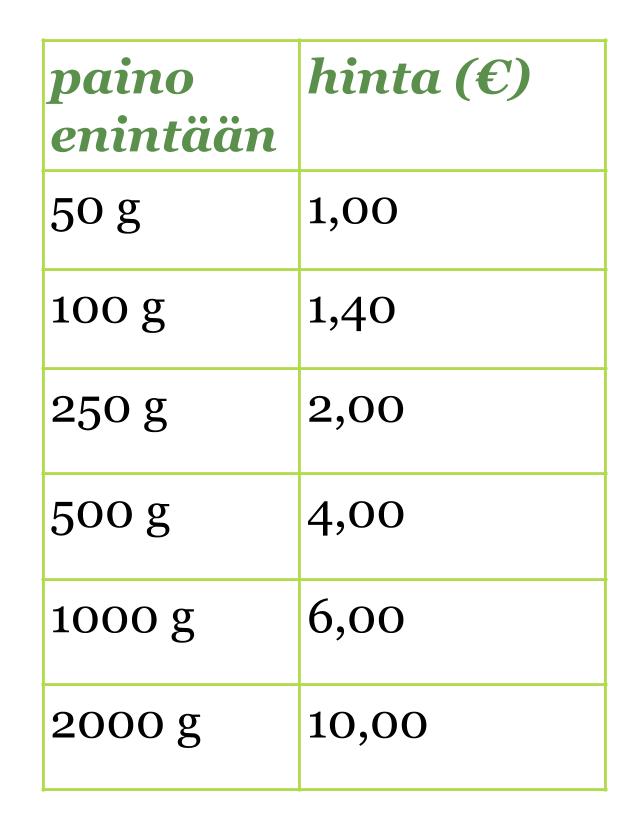
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Lähde: Yleisimmät postimaksut Suomessa 1.1.2014 alkaen, www.posti.fi
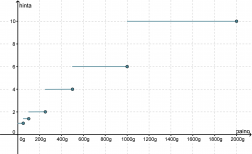
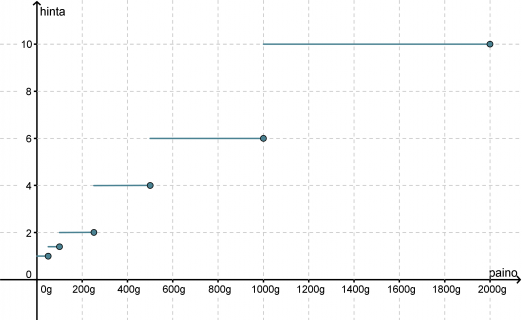
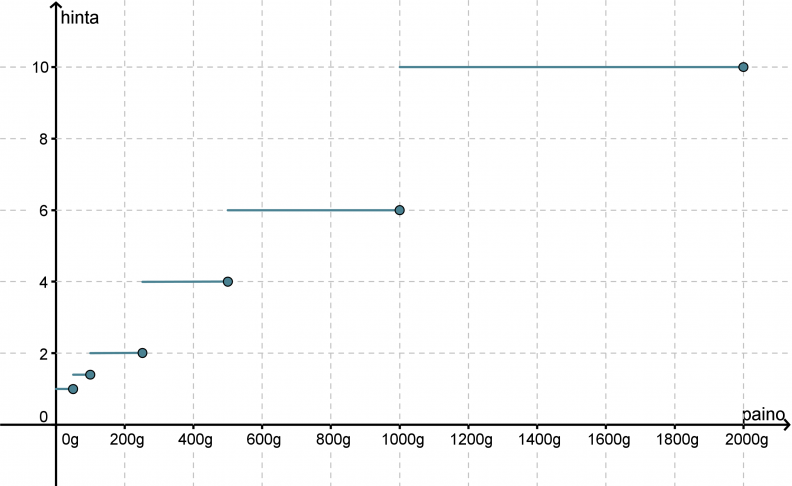
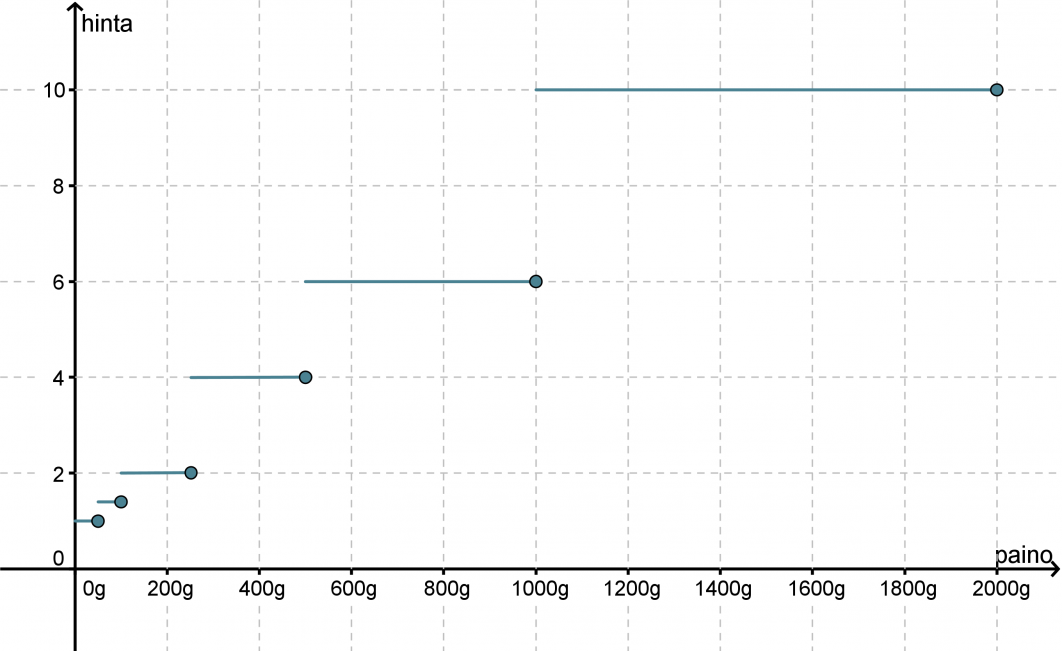
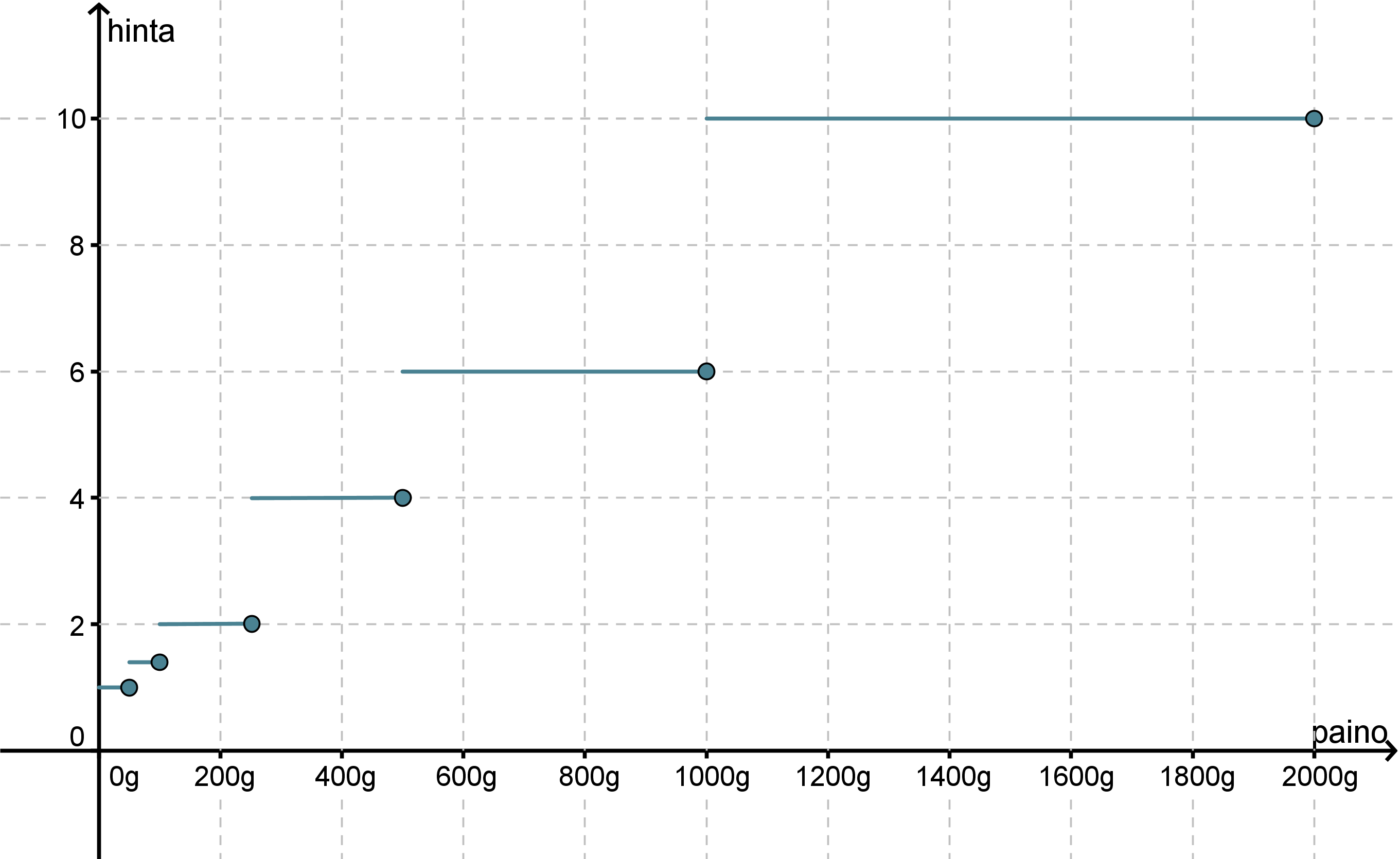
Piirretään kuvaaja kirjeen hinnan muodostumisesta painon suhteen.
Ei ole merkitystä painaako kirje 505 grammaa vai hieman alle kilon, hinta on kuitenkin sama 4,00 €. Tällöin kuvaaja välillä 500 g – 1000 g on vaaka-akselin suuntainen suora. Kun paino ylittää 1 kg, hypähtää maksu 6,00 euroon ja pysyttelee siellä, kunnes paketin paino on yli 2 kg. Kuvaaja muodostuu siten vaaka-akselin suuntaisista palasista. Vaakasuuntaisten viivojen lopussa olevat ympyrät korostavat sitä pistettä, jolta funktion arvo on liitoskohdissa luettava. Funktiokäsitteen määritelmän mukaan funktiolla ei saa olla yhdessä kohdassa kuin yksi arvo!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
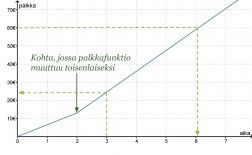
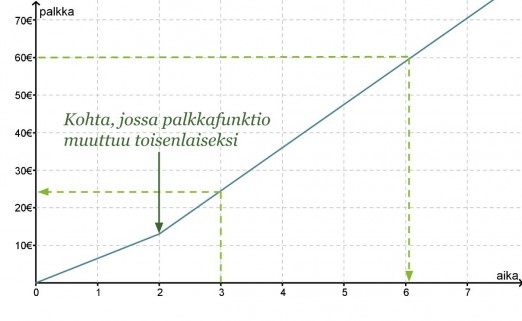
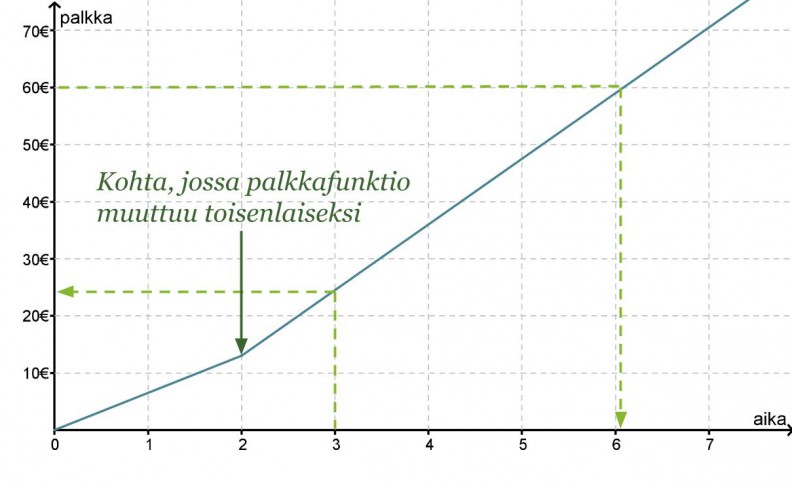
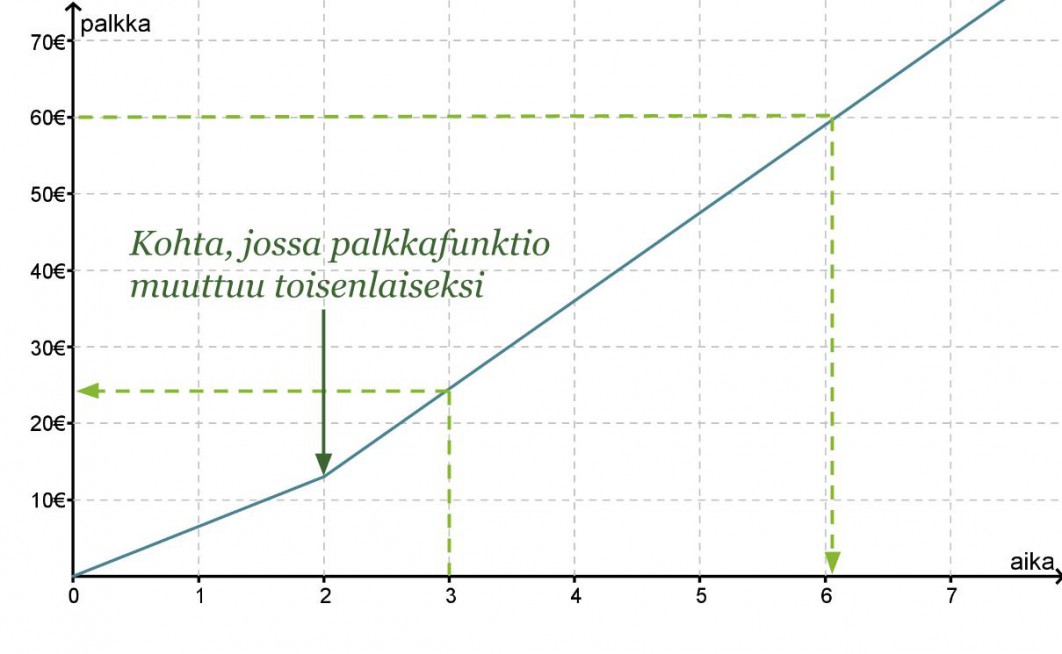
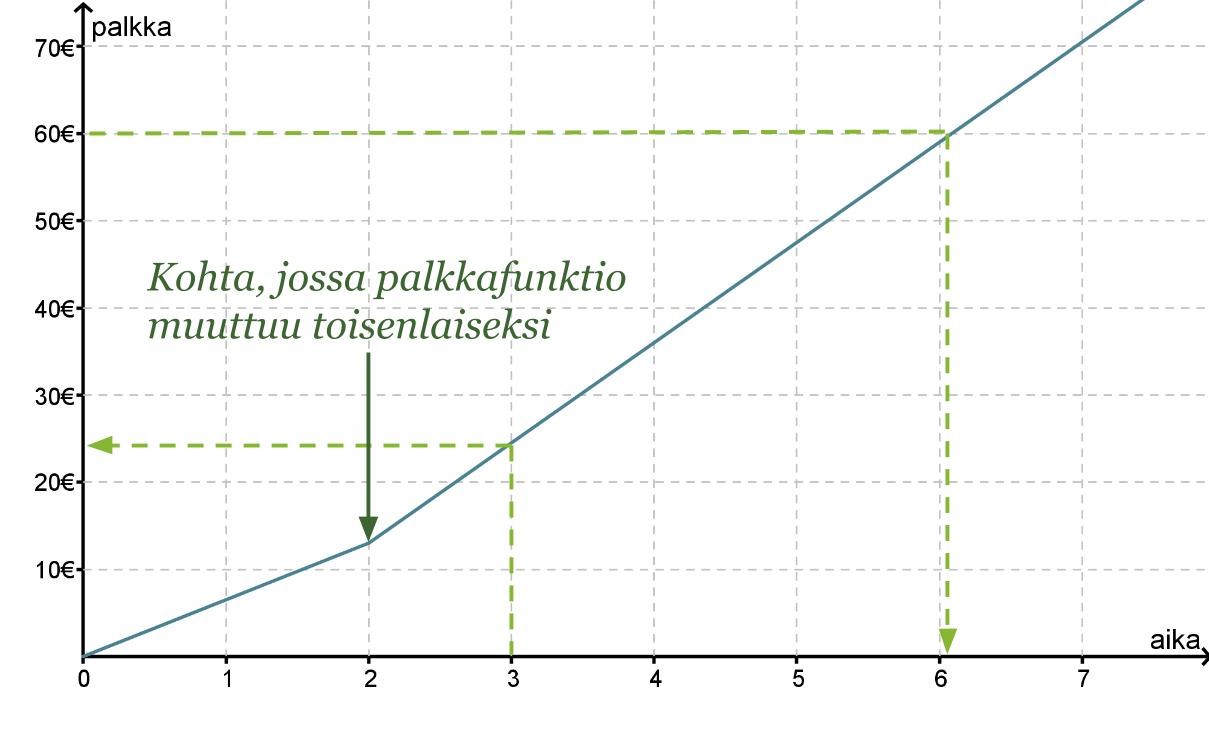
Leevin päiväkohtainen palkka muodostui siten, että kahden ensimmäisen tunnin palkka oli 6,50 € / h ja sitä seuraavien tuntien palkka 11,50 € / h. Muodostetaan Leevin palkkafunktion lauseke.
Piirretään Leevin palkasta ensin kuvaaja, jonka avulla selvitetään yhtälöt.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kahden ensimmäisen tunnin palkka saadaan yhtälöstä y = 6,50 x.
Jotta pystytään määrittämään suoralle yhtälö, joka kuvaa palkkausta kahden tunnin jälkeen, otetaan kahden tunnin kohdalta alkavalta suoralta kaksi tarkastelupistettä (x1, y1) ja (x2, y2), joiden avulla lasketaan suoran kulmakerroin.

Klikkaa kuva suuremmaksi!
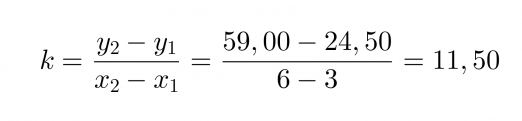
Klikkaa kuva suuremmaksi!
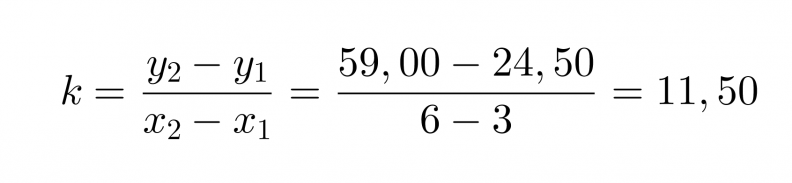
Klikkaa kuva suuremmaksi!
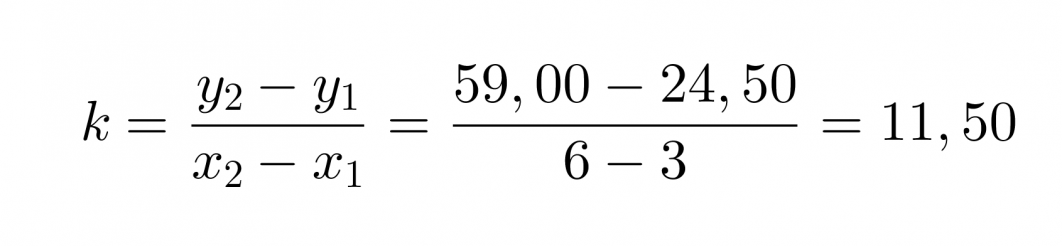
Klikkaa kuva suuremmaksi!
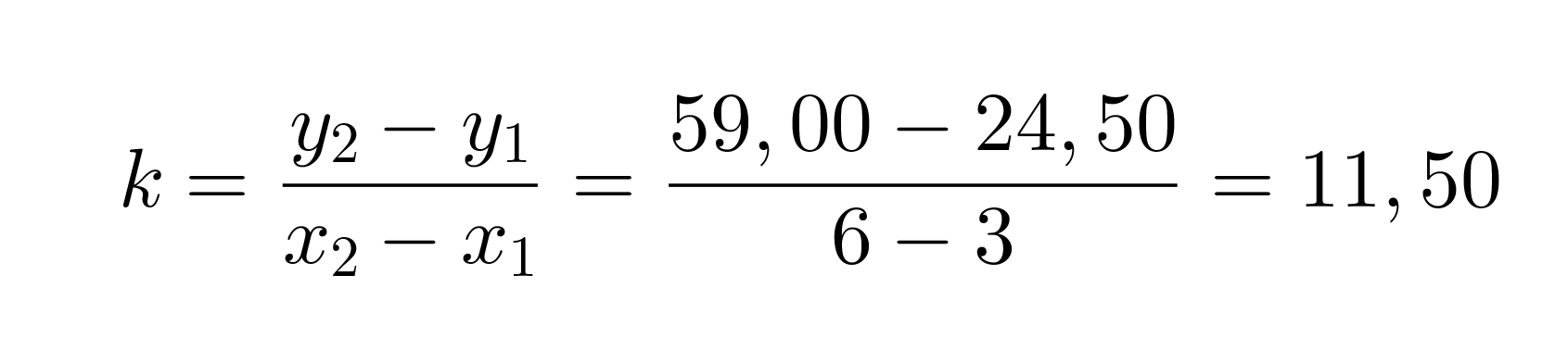
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
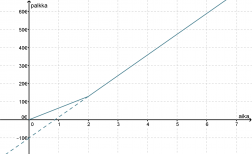
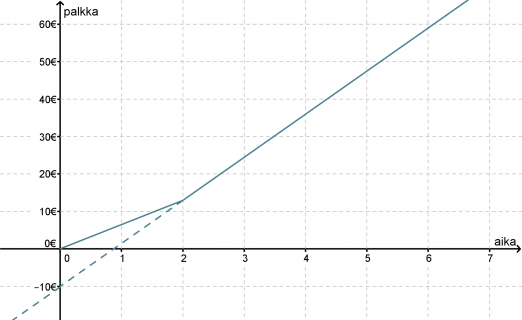
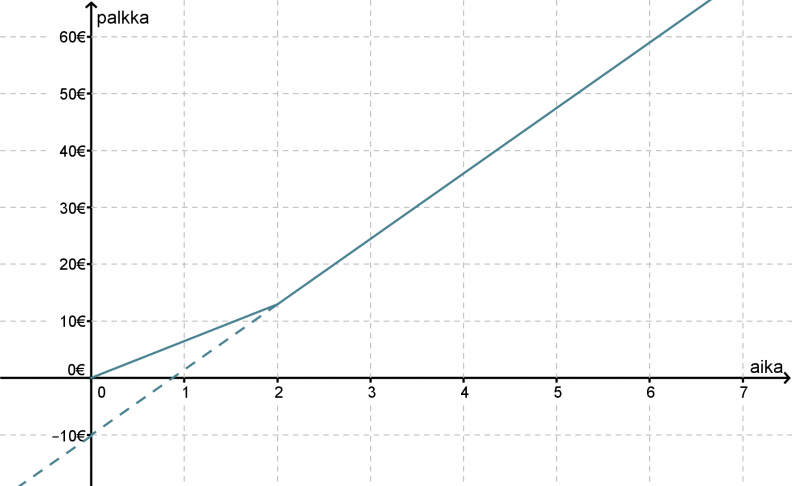
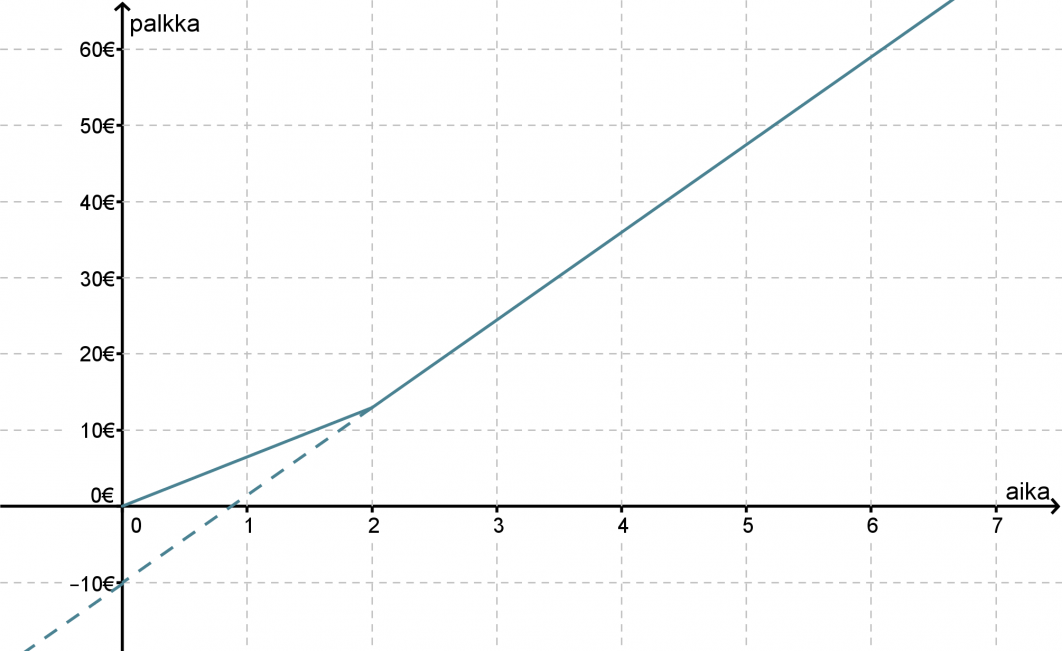
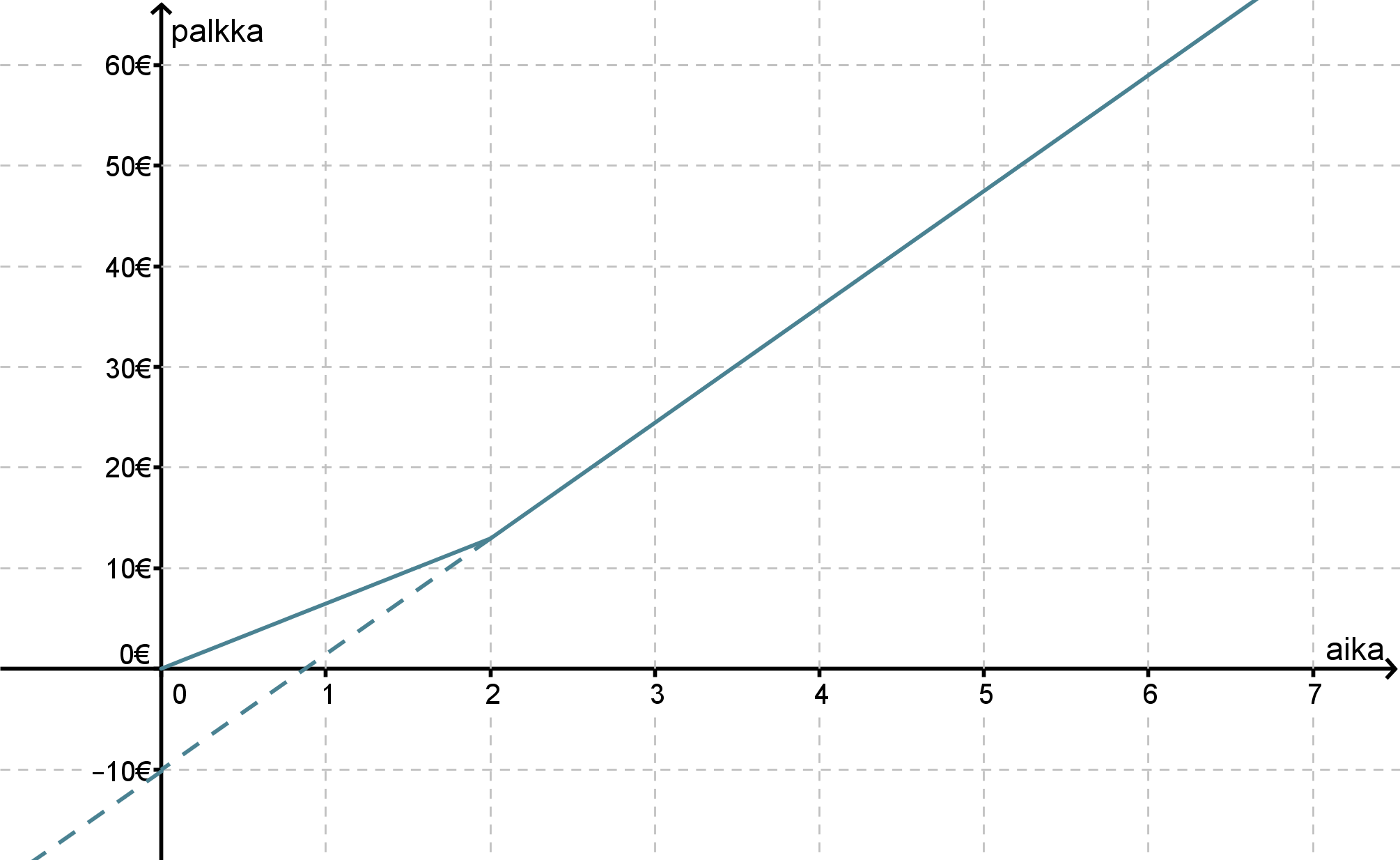
Yhtälön kirjoittamista varten pitäisi vielä tietää kohta, jossa kuvaaja leikkaa y-akselin. Määritetään leikkauskohta piirtämällä suoralle jatke.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Suoran jatke leikkaa y-akselin kohdassa y = −10, joten suoran yhtälö on y = 11,50x − 10.
Kahden ensimmäisen tunnin ajalta palkka saadaan lasketuksi yhtälöllä y = 6,50x ja kahden tunnin jälkeen yhtälöllä y = 11,50x − 10. Paloittain määritellyn funktion lauseke kirjoitetaan muodossa
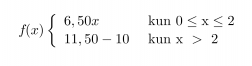
Klikkaa kuva suuremmaksi!
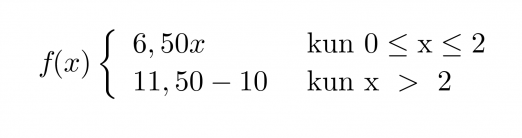
Klikkaa kuva suuremmaksi!
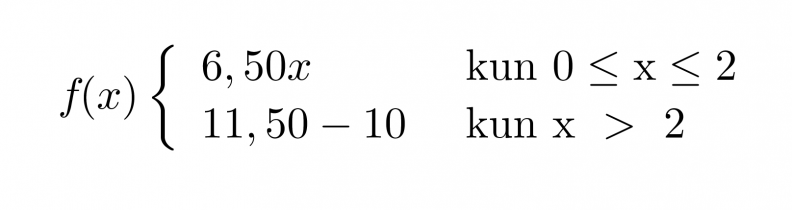
Klikkaa kuva suuremmaksi!
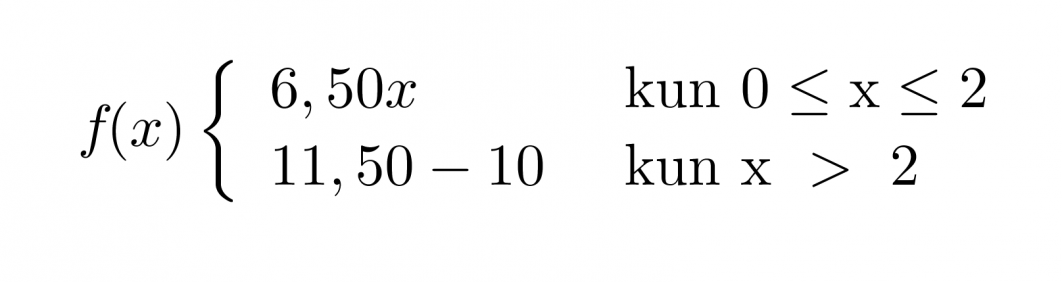
Klikkaa kuva suuremmaksi!
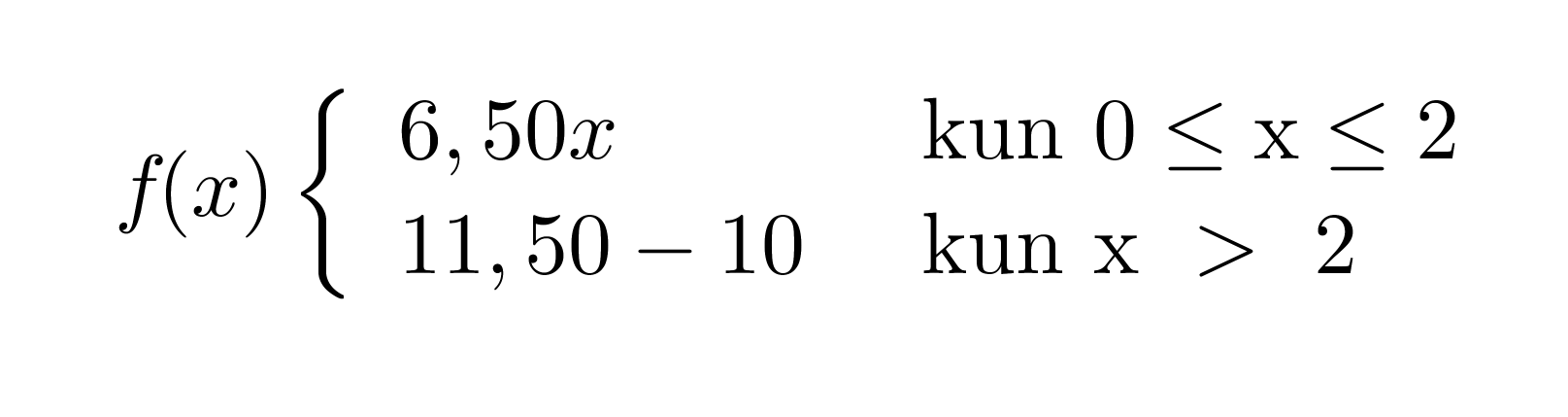
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Tekemättömistä tunneista ei makseta palkkaa, joten funktiota ei ole järkevää käyttää negatiivisille arvoille, tästä tulee ehto 0 ≤ x ≤ 2 eikä pelkästään x ≤ 2.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014