7. Havainnoista funktioksi*

Maa­il­maa hal­lit­se­vat yk­sin­ker­tai­set ma­te­maat­ti­set lait ja ma­te­maat­ti­sia käy­riä esiin­tyy lä­hes kaik­ki­al­la. Tie­teel­li­nen kek­si­mi­nen on itse asi­as­sa ma­te­maat­tis­ten yh­tä­löi­den löy­tä­mis­tä eri­lais­ten ko­kei­den avul­la. Mit­tauk­sia teh­dään muut­te­le­mal­la eri suu­rei­den ar­vo­ja ja si­joit­ta­mal­la nämä ha­vain­to­pis­teet koor­di­naa­tis­toon. Tie­de­mies ko­kee on­nis­tu­mi­sen, jos ma­te­maat­ti­nen käy­rä so­pii hy­vin ha­vain­to­pis­tei­siin. Käy­rän löy­ty­mi­nen on merk­ki sii­tä, että tut­kit­tu­jen suu­rei­den vä­lil­le voi­daan kir­joit­taa ma­te­maat­ti­nen yh­tä­lö. Jos­kus ku­vaa­jis­ta tu­lee sel­lai­sia, että on syy­tä käyt­tää pa­loit­tain mää­ri­tet­ty­jä funk­ti­oi­ta käyt­täy­ty­mis­tä ku­vaa­van yh­tä­lön löy­tä­mi­sek­si. Yleen­sä tie­de­tään etu­kä­teen min­kä­lai­nen funk­ti­o­tyyp­pi havaintopisteikköön so­pii.

Esimerkki 1.

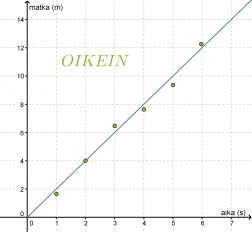
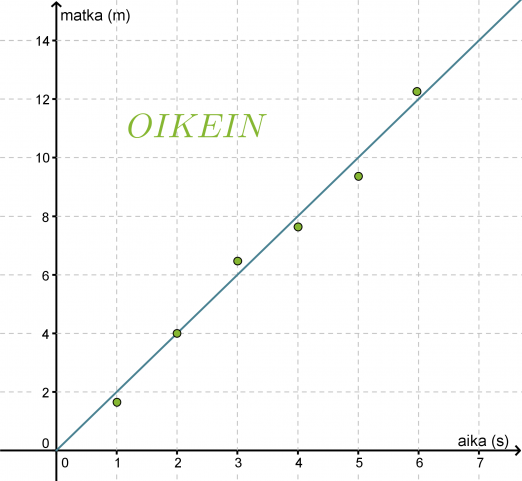
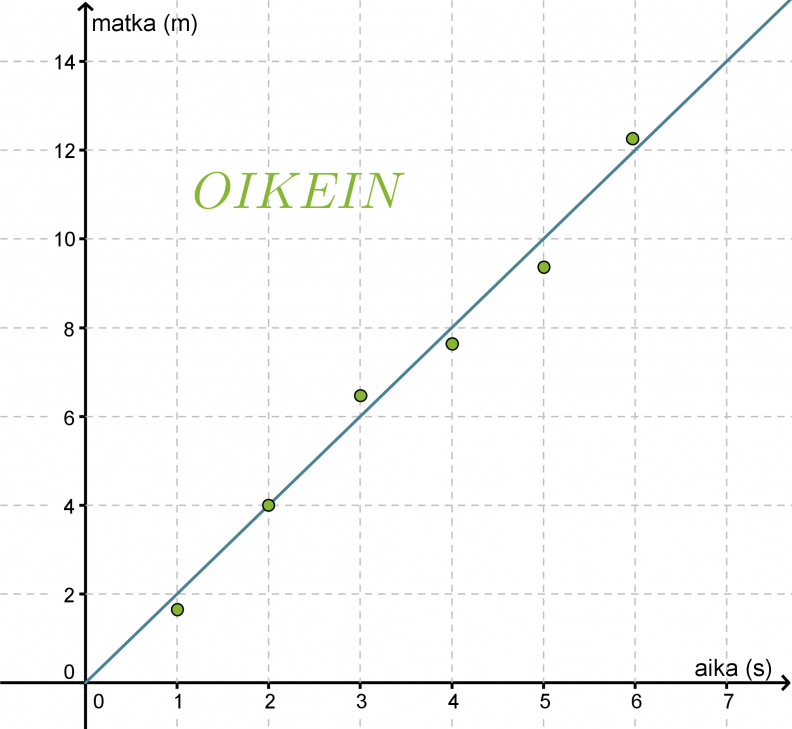
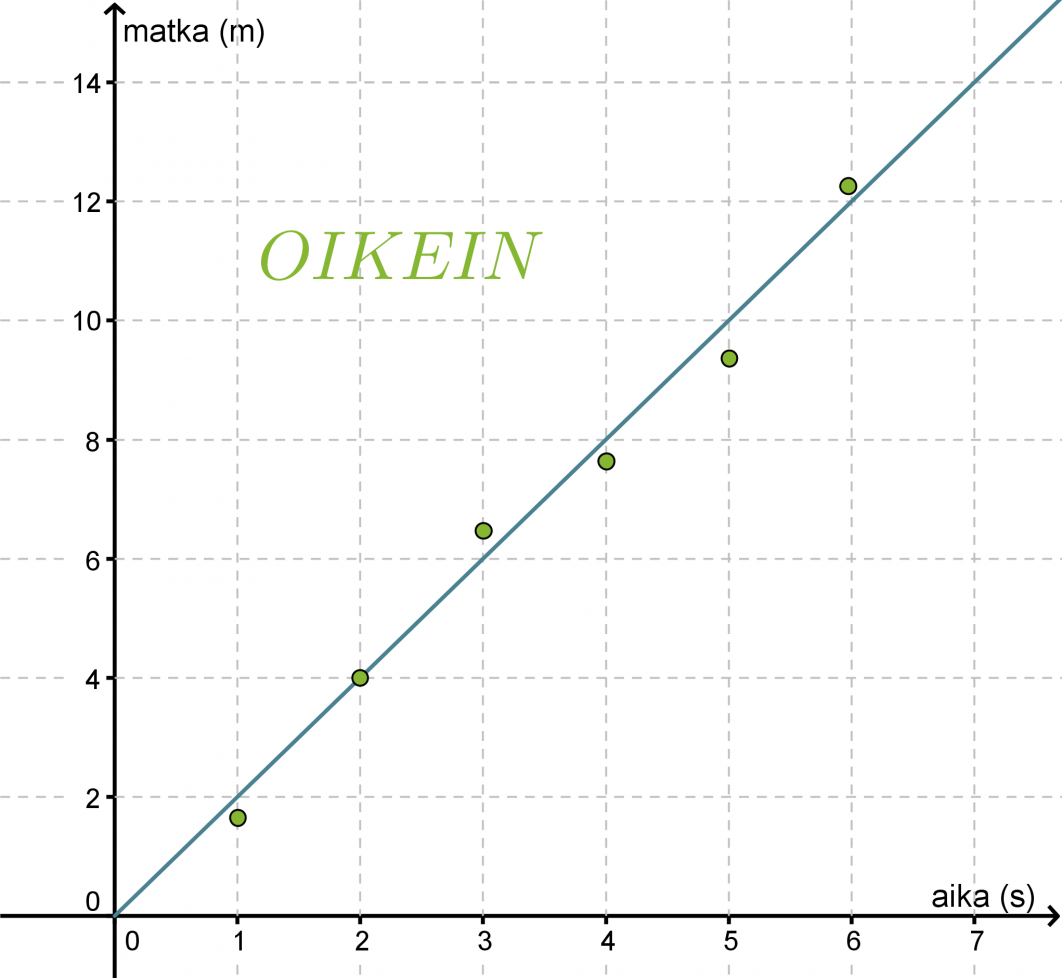
Tut­ki­taan kä­ve­li­jän kul­ke­maa mat­kaa ajan funk­ti­o­na. Mi­ta­taan kul­jet­tu mat­ka se­kun­nin vä­lein ja si­joi­te­taan ha­vain­to­pis­teet aika, mat­ka –koor­di­naa­tis­toon.

Klik­kaa kuva suu­rem­mak­si!

Klik­kaa kuva suu­rem­mak­si!

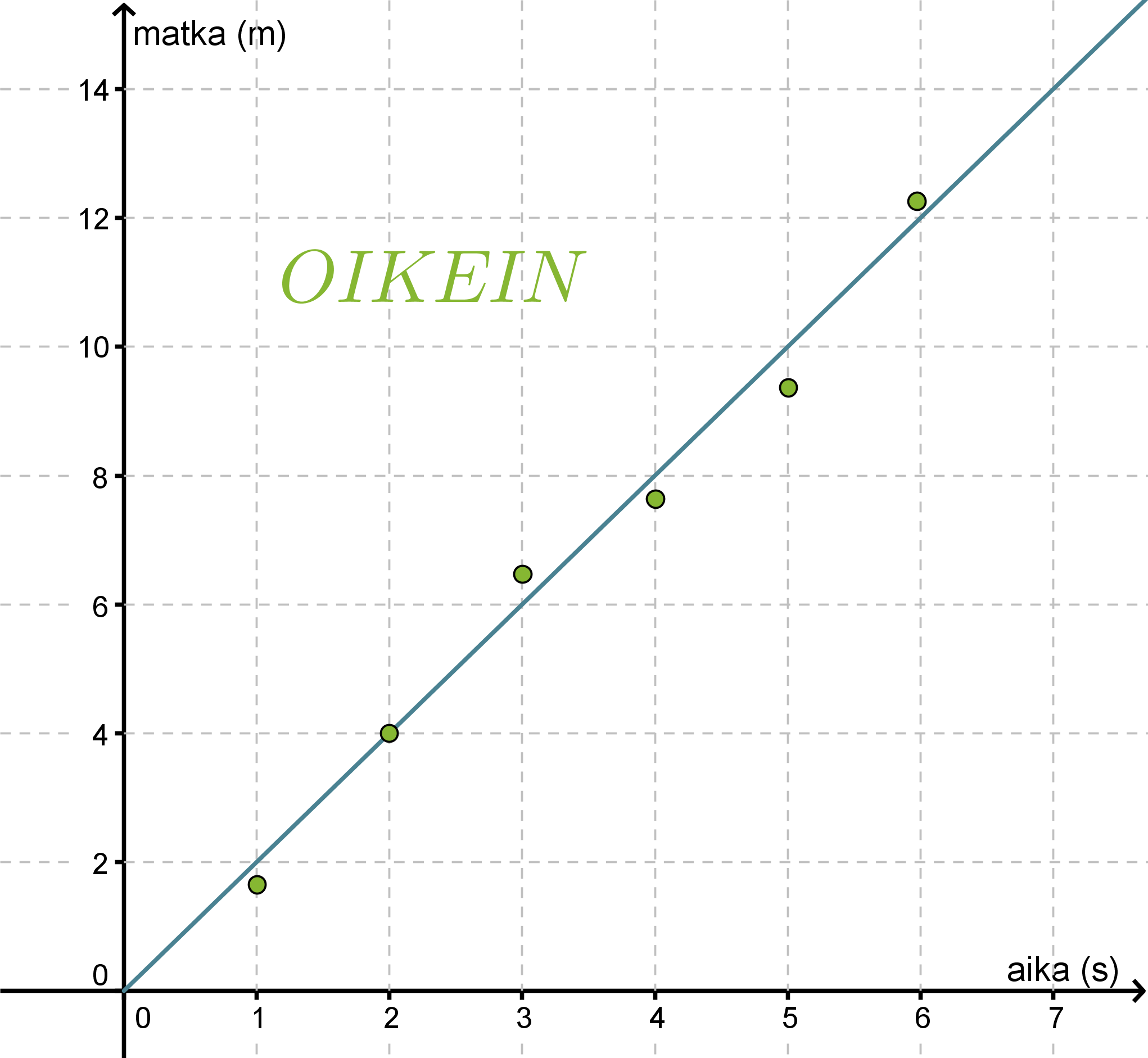
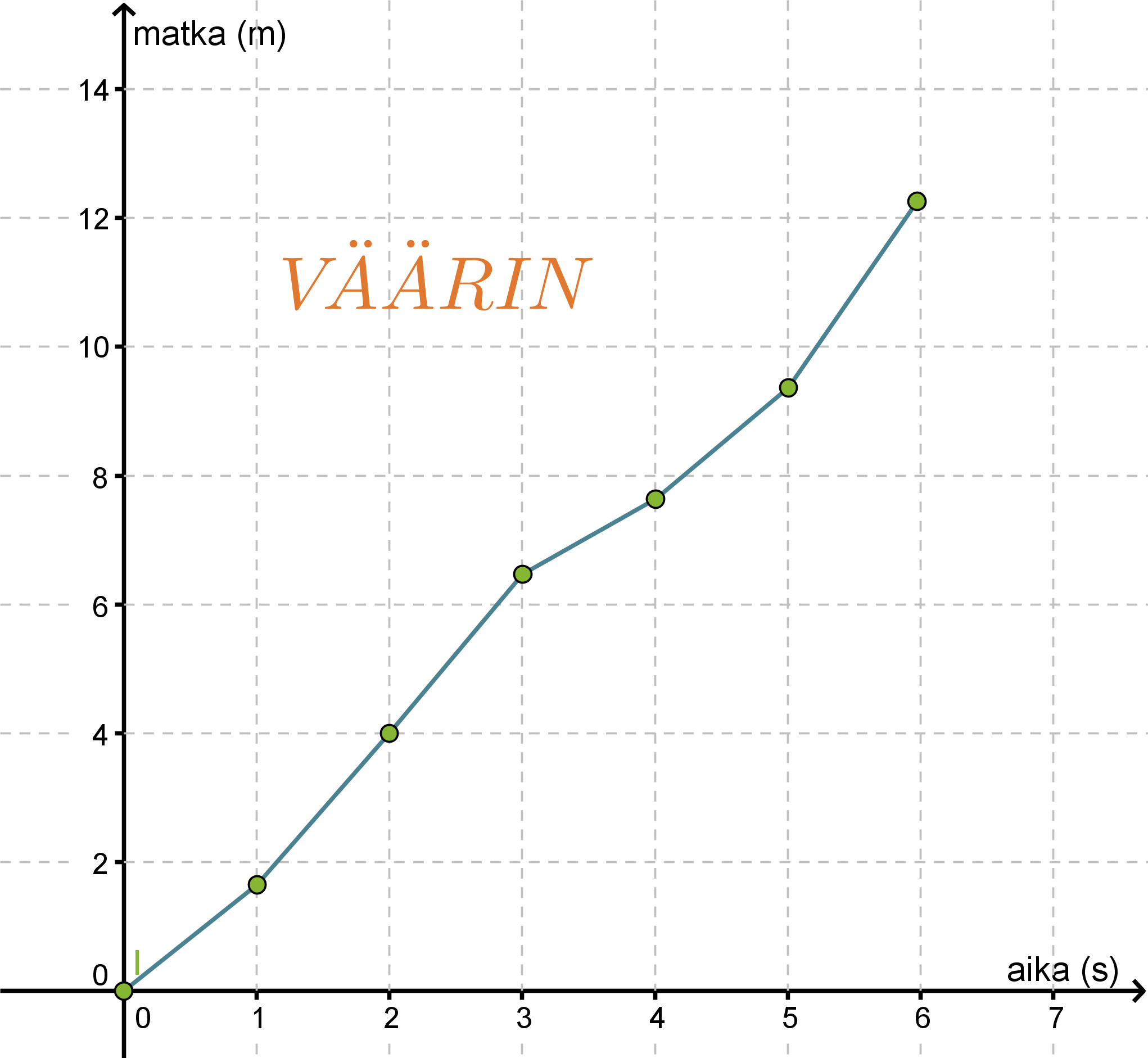
Ha­vain­to­pis­teet näyt­tä­vät osu­van hy­vin ori­gon kaut­ta kul­ke­val­le suo­ral­le, jo­ten piir­re­tään suo­ra ha­vain­to­pis­tei­den vä­liin si­ten, että suo­ran mo­lem­mil­le puo­lil­le jää yhtä pal­jon ha­vain­to­pis­tei­tä. Mit­tauk­sis­sa esiin­tyy aina vir­hei­tä ja jos joku mit­taus­pis­te poik­ke­aa huo­mat­ta­vas­ti muis­ta pis­teis­tä, voi­daan se tul­ki­ta vir­heel­li­sek­si ja jät­tää huo­mi­oi­mat­ta funk­ti­o­ta so­vi­tet­ta­es­sa. Täs­sä kaik­ki ha­vain­to­pis­teet voi­daan kui­ten­kin to­de­ta on­nis­tu­neik­si mit­tauk­sik­si.

Pis­tei­tä ei siis yh­dis­te­tä tar­kas­ti toi­siin­sa, ku­ten yllä ole­vas­sa VÄÄ­RIN –ku­vas­sa on teh­ty. Täl­löin­hän muo­dos­tet­tai­siin jouk­ko pa­loit­tain mää­ri­tel­ty­jä funk­ti­oi­ta, joi­den käyt­tö ei täs­sä tar­koi­tuk­ses­sa ole mie­le­käs­tä. Kä­ve­li­jän no­peus luon­nol­li­ses­ti vaih­te­lee, mut­ta täs­tä ai­heu­tu­van vir­heen funk­ti­on lau­sek­kee­seen saa­daan pois­tet­tua si­ten, että suo­ra to­del­la­kin si­joi­te­taan ha­vain­to­pis­tei­den vä­liin.

Mer­ki­tään ai­kaa x:llä ja mat­kaa y:llä. Va­li­taan suo­ral­ta kak­si pis­tet­tä yh­tä­lön kul­ma­ker­toi­men mää­rit­tä­mi­sek­si. Ol­koon nämä ori­go (0, 0) ja pis­te (3, 6). Kul­ma­ker­toi­mek­si saa­daan

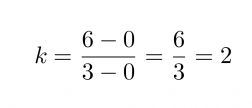
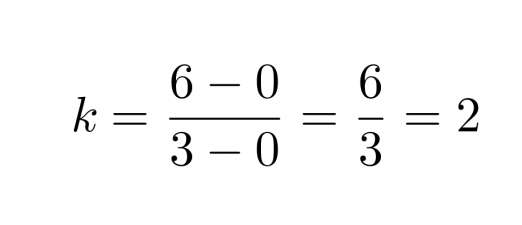
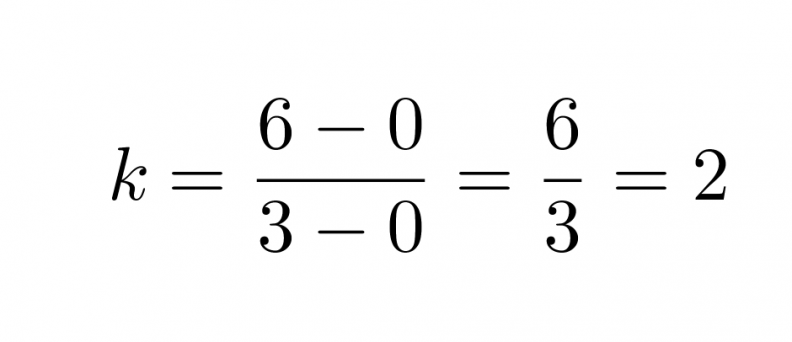
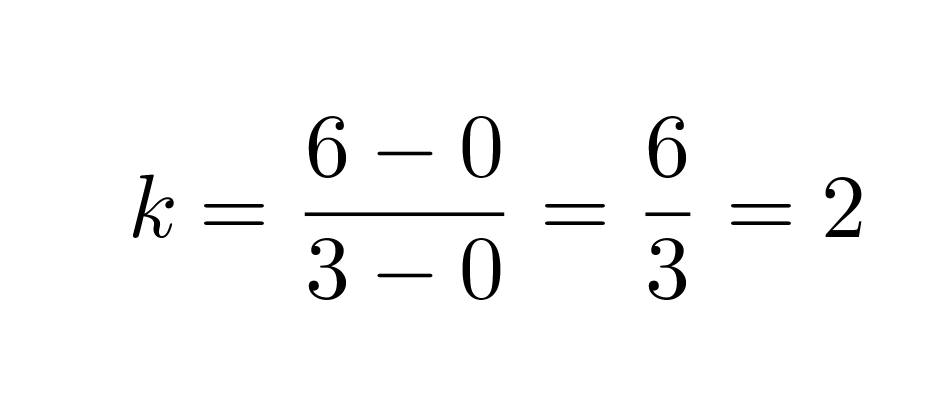
Klik­kaa kuva suu­rem­mak­si!

Si­joi­te­taan kul­ma­ker­roin ja pis­te (0, 0) suo­ran yh­tä­löön, jol­loin saa­daan

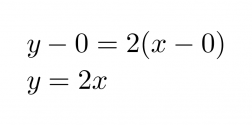
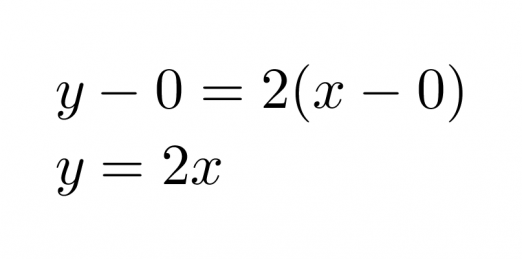
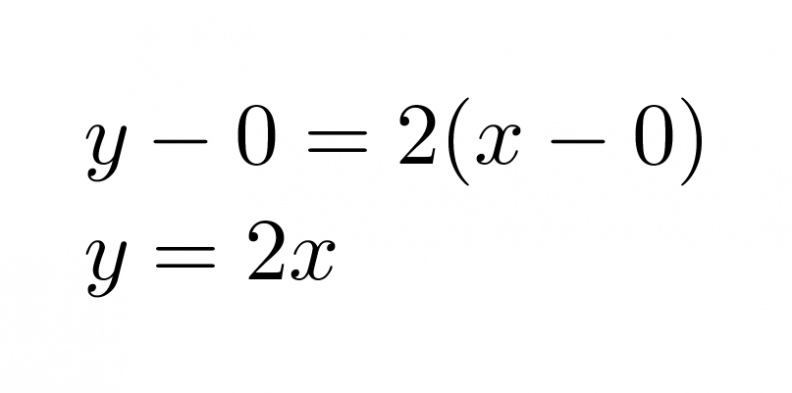
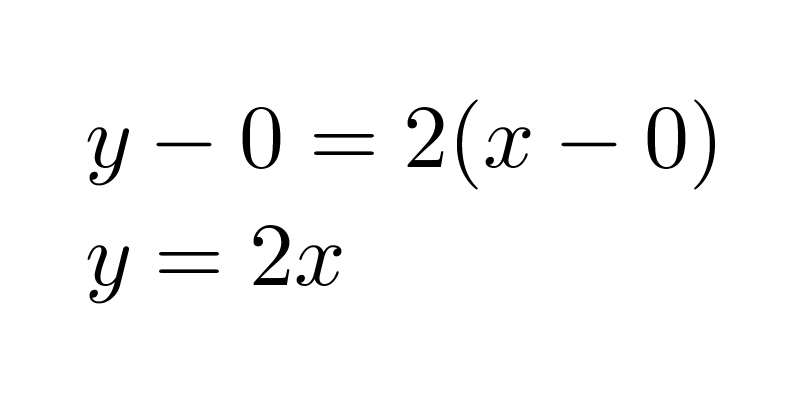
Klik­kaa kuva suu­rem­mak­si!

Esi­mer­kis­sä 1 muo­dos­tet­tiin ta­sai­sen liik­keen yh­tä­lö mat­ka = no­peus · aika. Yh­tä­löä käy­te­tään kaik­ki­al­la, sitä enem­pää ky­seen­a­lais­ta­mat­ta. En­nen kuin tämä yh­tä­lö hy­väk­syt­tiin ylei­ses­ti, jou­tui­vat tie­de­mie­het te­ke­mään val­ta­van mää­rän mit­tauk­sia ja ma­te­maat­tis­ten funk­ti­oi­den so­vi­tuk­sia.