Fibonaccin lukujono

Fibonacci eli Le­o­nar­do Pi­sa­lai­nen oli ita­li­a­lai­nen ma­te­maa­tik­ko ja kaup­pi­as, joka eli vuo­den 1200 tie­noil­la. Hän on kes­ki­ajan tun­ne­tuim­pia eu­roop­pa­lai­sia ma­te­maa­tik­ko­ja. Fibonacci poh­dis­ke­li seu­raa­van­lais­ta on­gel­maa:

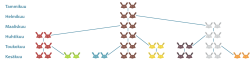
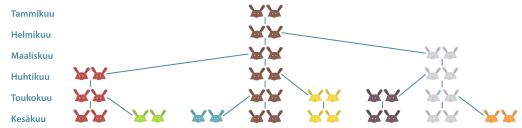
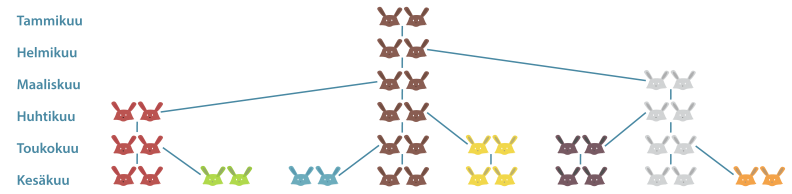
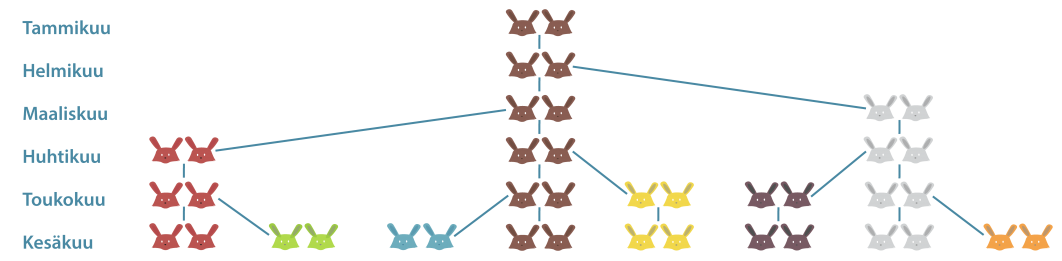
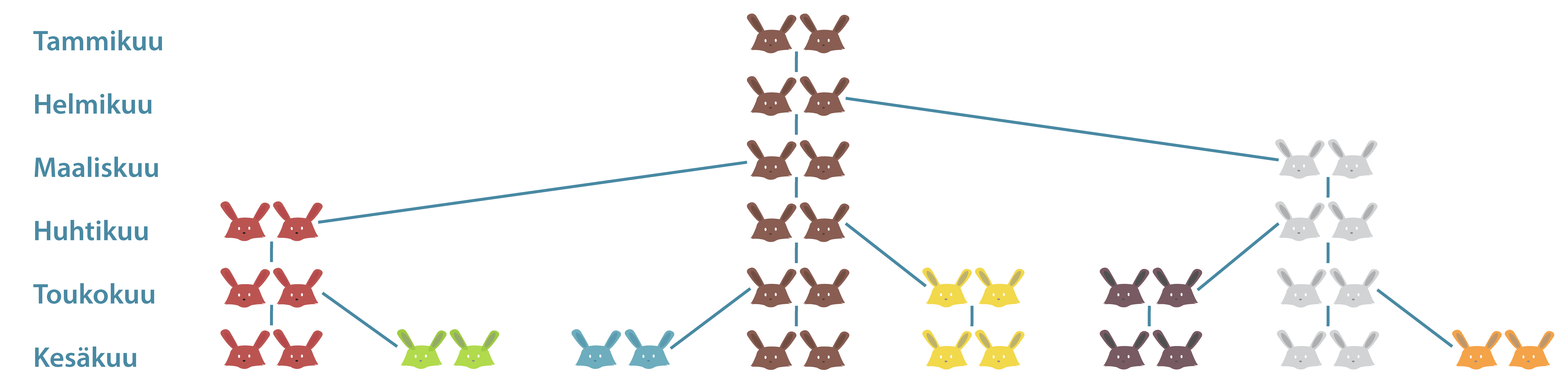
Vuo­den alus­sa ai­tauk­ses­sa on vas­ta­syn­ty­nyt kani­pari. Kani­pa­rit syn­nyt­tä­vät kah­den kuu­kau­den iäs­tä läh­tien kuu­kau­den vä­lein yh­den naa­raan ja yh­den urok­sen, jot­ka kaik­ki jat­ka­vat li­sään­ty­mis­tään sa­mal­la ta­val­la. Mon­ta­ko kani­pa­ria on vuo­den ku­lut­tua?

En­sim­mäi­sen kuu­kau­den alus­sa on yksi kani­pari ja sa­moin toi­sen kuu­kau­den alus­sa on yksi kani­pari. Kol­man­nen kuu­kau­den alus­sa kani­pari syn­nyt­tää uu­den kani­pa­rin, jo­ten kani­pa­re­ja on nyt kak­si. En­sim­mäi­nen kani­pari syn­nyt­tää taas nel­jän­nen kuu­kau­den alus­sa, jo­ten kani­pa­re­ja on nyt kol­me. Vii­den­nen kuu­kau­den alus­sa sekä en­sim­mäi­nen että toi­nen kani­pari syn­nyt­tä­vät uu­den pa­rin, jo­ten kani­pa­re­ja on sil­loin vii­si jne. Näin jat­ka­en kani­pa­re­ja on 12. kuu­kau­den alus­sa 144.

Kani­pa­rien luku­mää­räs­tä muo­dos­tuu Fibonaccin luku­jono, jos­sa kak­si en­sim­mäis­tä lu­kua ovat yk­kö­siä ja muut lu­vut saa­daan las­ke­mal­la kak­si edel­lis­tä lu­kua yh­teen. Kak­si­tois­ta en­sim­mäis­tä Fibonaccin luku­jo­non lu­ku­ja ovat siis 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ja 144.

Fibonaccin luku­jo­non lu­vut esiin­ty­vät luon­nos­sa mo­nis­sa yh­teyk­sis­sä. Jo itse Fibonacci ha­vait­si ai­ka­naan, että kuk­kien terä­leh­tien luku­mää­rä on yleen­sä jo­kin luku­jo­non lu­vuis­ta. Esi­mer­kik­si päi­vän­kak­ka­ral­la voi olla 34, 55 tai jopa 89 terä­leh­teä. Li­säk­si mo­nien kas­vien leh­ti­kieh­ku­ras­sa kah­den pe­räk­käi­sen leh­den suun­tien ero­tus on 3/5 täy­des­tä kier­rok­ses­ta.

Klik­kaa kuva suu­rem­mak­si!