8. Lukujonoja
Kun lukuja asetetaan peräkkäin pilkuilla erotettuina, muodostuu lukujono. Lukujono voi olla päättyvä tai päättymätön. Päättymättömän jonon lopussa on kolme pistettä.
Lukujonon 1, 4, 7, 10, 13,… seuraavat luvut ovat helposti pääteltävissä, sillä ne muodostuvat tietyn säännön mukaan.
Lukujono (an) on luvuista muodostuva jono, joka voidaan esittää luettelona a1, a2, a3, …, missä jonon jäseniä sanotaan termeiksi tai alkioiksi.
Luku a1 on lukujonon 1. termi ja a2 on sen 2. termi jne. Lukujonon termiä, jonka järjestysluku on n, sanotaan sen yleiseksi termiksi, ja sitä merkitään an.
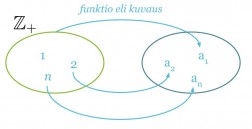
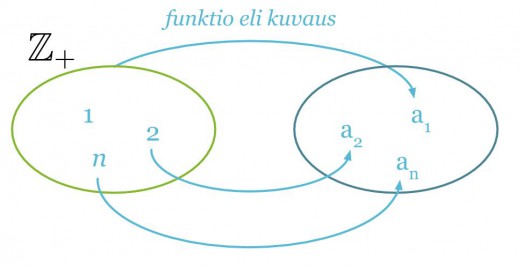
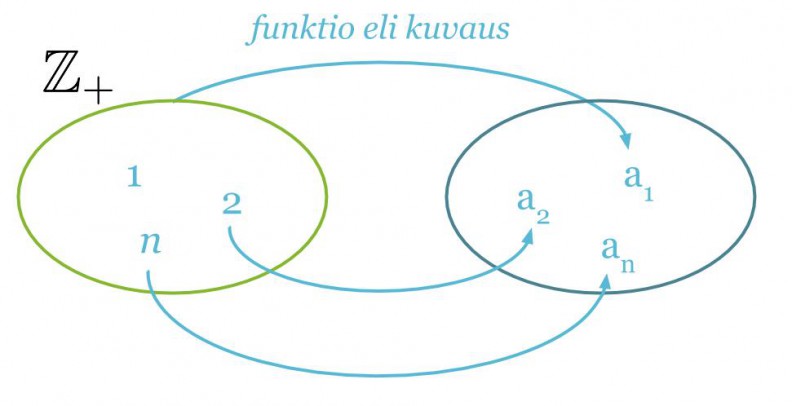
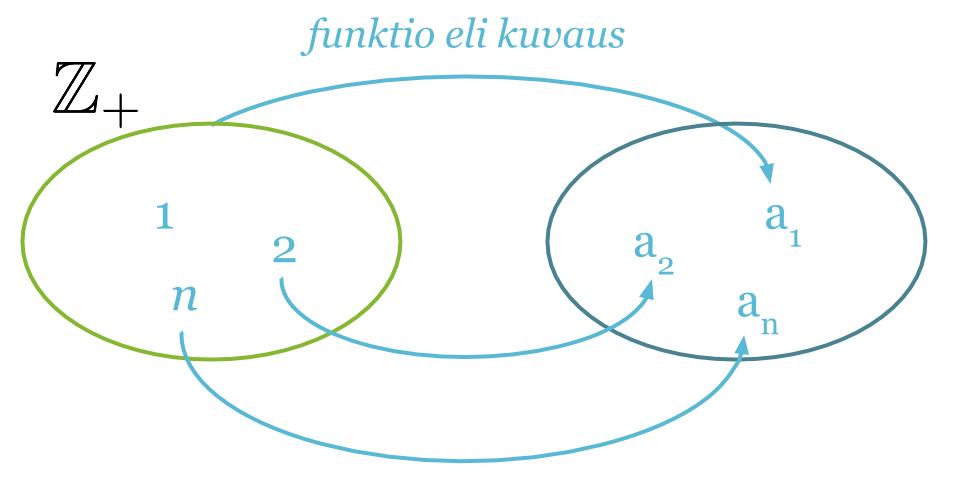
Lukujono voidaan ajatella funktiona, jonka määrittelyjoukko on {1, 2, 3, …, n} ja arvojoukko {f(1), f(2), f(3), …, f(n)}. Lukujonon termit voidaan siten luetella sijoittamalla funktioon muuttujan paikalle termin järjestysnumero. Yleisesti lukujonoissa käytetään muuttujana kirjainta n.
Lukujono muodostuu yleensä tietyn säännön mukaan, jolloin termin järjestysluvun n avulla saadaan itse termi. Sääntö voidaan usein tulkita positiivisten kokonaislukujen 1, 2, 3, 4, … ja jonon termien väliseksi funktioksi f(n) = an.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
Määritetään lukujonon kolme ensimmäistä termiä ja 15. termi, kun yleinen termi on an = 3 + 2n.
n kuvaa termin järjestyslukua, joten ensimmäinen termi saadaan, kun luvun n paikalle sijoitetaan 1 jne.
a1 = 3 + 2 · 1 = 5
a2 = 3 + 2 · 2 = 7
a3 = 3 + 2 · 3 = 9
a15 = 3 + 2 · 15 = 33
Esimerkki 2.
Mikä on lukujonon sadas termi?

Klikkaa kuva suuremmaksi!
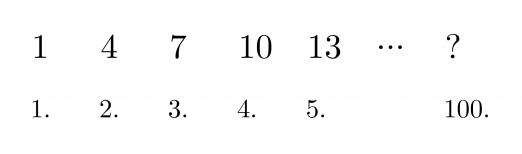
Klikkaa kuva suuremmaksi!
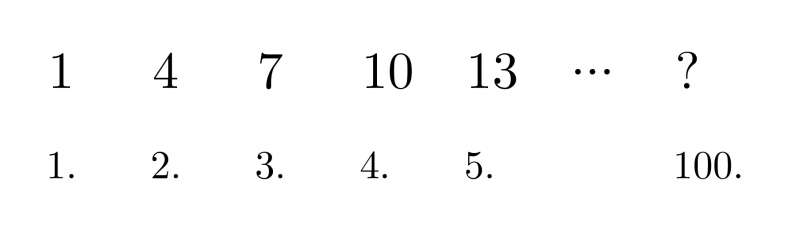
Klikkaa kuva suuremmaksi!
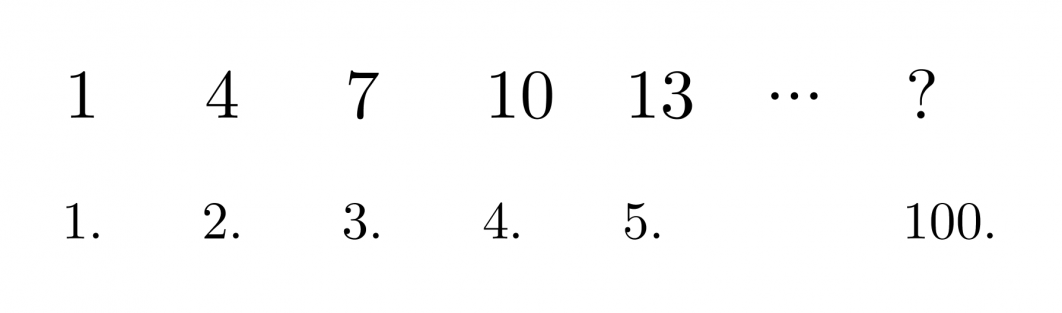
Klikkaa kuva suuremmaksi!
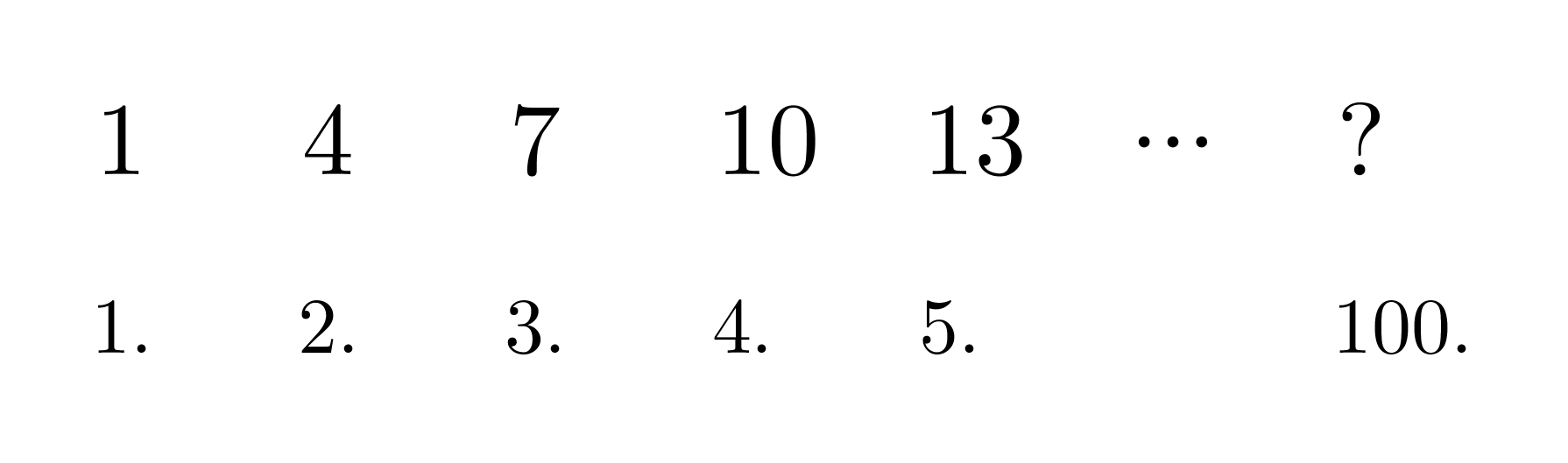
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaisu:
Lukujonon seuraava termi saadaan lisäämällä edelliseen termiin luku kolme. Olisi kovin työlästä selvittää vastaus käymällä läpi kaikki sata termiä. Onkin löydettävissä sääntö, miten lukujonon termit muodostuvat. Säännössä hyödynnetään termin järjestysnumeroa. Päättelyn apuna voidaan käyttää funktiokonetta, joka muodostaa kuvaukset seuraavasti:
1 → 1
2 → 4
3 → 7
4 → 10
5 → 13
Yleisesti toimintatapa voidaan esittää muodossa n → 3n − 2 eli lukujonon yleinen termi on an = 3n − 2. Sadas termi on tällöin 3 · 100 − 2 = 298.
Vastaus: 100. termi on 298
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014