9. Aritmeettinen lukujono
Lukujono on kasvava, jos jokainen termi on suurempi tai yhtä suuri kuin edellinen ja lukujono on vähenevä, jos jokainen termi on pienempi tai yhtä suuri kuin edellinen.
Luonnollisten lukujen joukko {0, 1, 2, 3, …} on esimerkki kasvavasta lukujonosta. Siinä kukin termi saadaan lisäämällä edelliseen luku 1. Tällaista jonoa, jossa termi saadaan edellisestä lisäämällä siihen sama vakio, sanotaan aritmeettiseksi lukujonoksi.
Tutkitaan miten aritmeettisen lukujonon yleinen termi an määräytyy lukujonon ensimmäisen termin a1 ja vakion d avulla

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
a2 = a1 + d
a3 = a2 + d = a1 + d + d = a1 + 2d
a4 = a3 + d = a1 + 2d + d = a1 + 3d
an = a1 + (n − 1)d
Aritmeettisessa lukujonossa kahden peräkkäisen termin erotus on vakio. Aritmeettisen lukujonon yleinen termi on
an = a1 + (n − 1)d
missä a1 on lukujonon ensimmäinen termi ja d erotusluku.
Esimerkki 1.
Luvulla 10 jaolliset luonnolliset luvut muodostavat aritmeettisen lukujonon (0, 10, 20, 30,…). Erotusluku d on 10 ja yleinen termi on
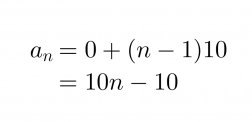
Klikkaa kuva suuremmaksi!
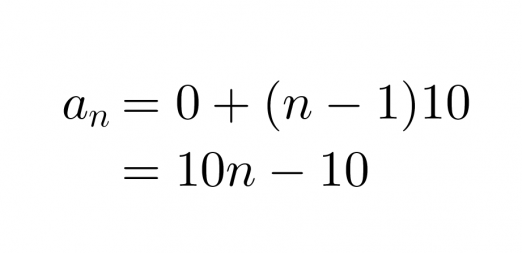
Klikkaa kuva suuremmaksi!
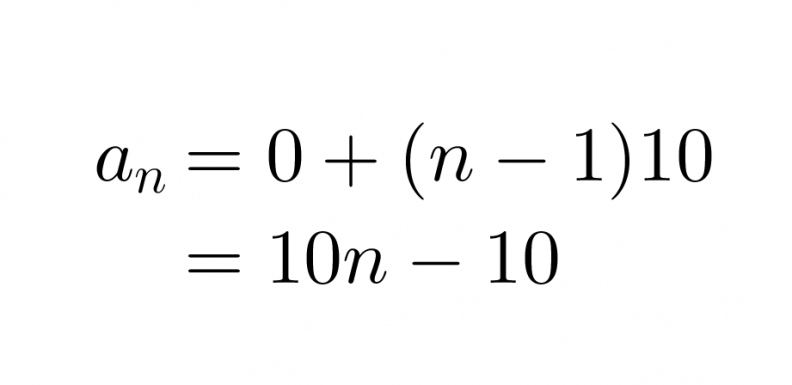
Klikkaa kuva suuremmaksi!
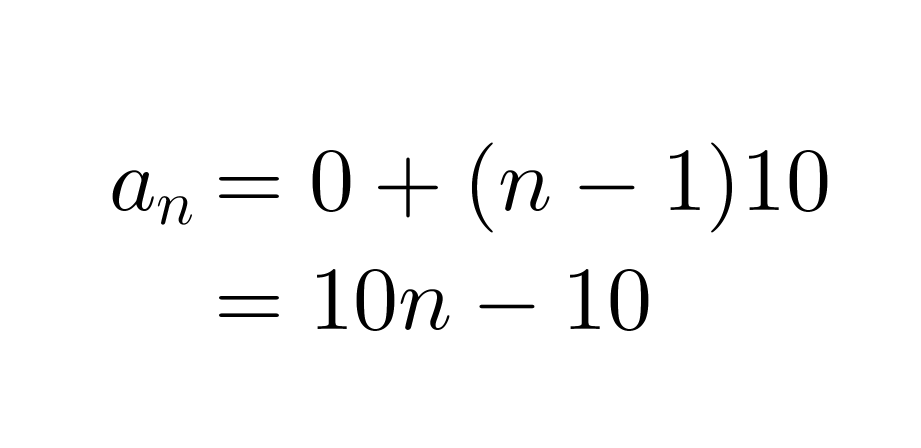
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Oskari aloittaa säästämisen tablettitietokonetta varten. Hänellä on säästössä valmiiksi jo 100 € ja joka viikko hän laittaa säästöön 8 €. Lasketaan, paljonko rahaa Oskarilla on 20 viikon jälkeen.
Kyseessä on aritmeettinen lukujono, jonka ensimmäinen termi on a1 = 100 ja erotusluku d = 8. Näiden avulla saadaan lukujonon yleinen termi
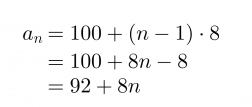
Klikkaa kuva suuremmaksi!
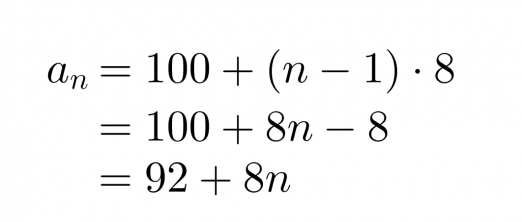
Klikkaa kuva suuremmaksi!
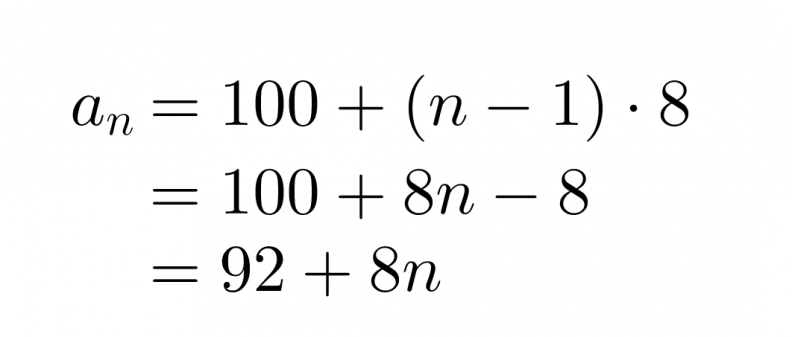
Klikkaa kuva suuremmaksi!
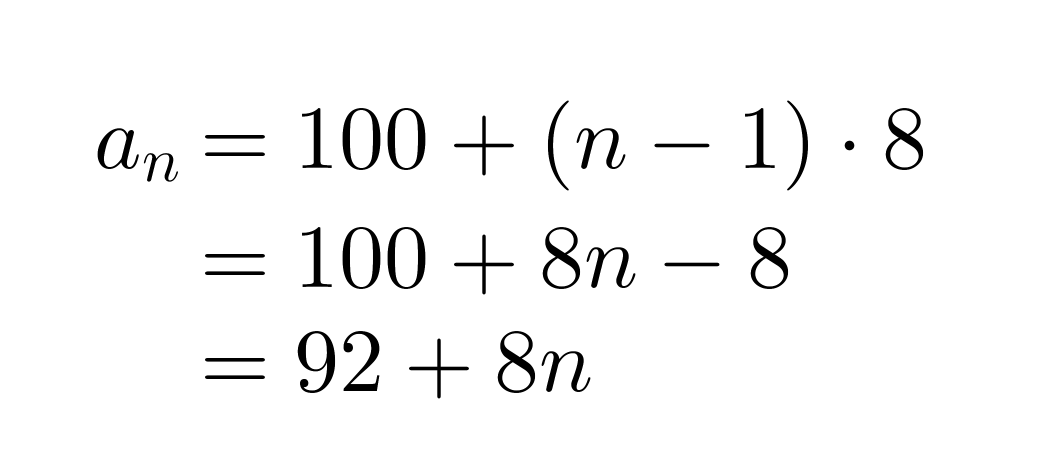
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
jonka avulla voidaan laskea lukujonon 20. termi
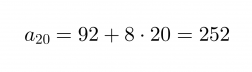
Klikkaa kuva suuremmaksi!
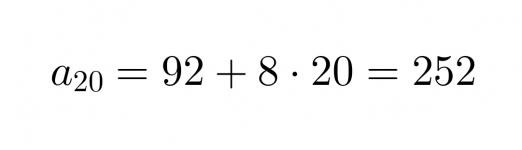
Klikkaa kuva suuremmaksi!
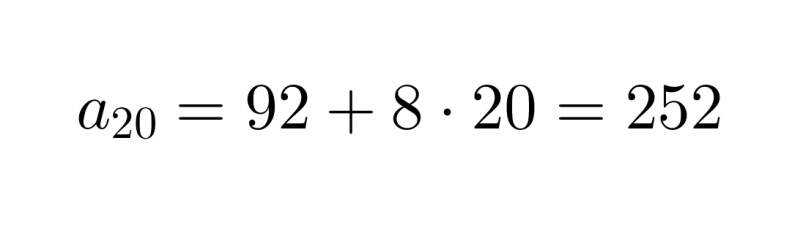
Klikkaa kuva suuremmaksi!
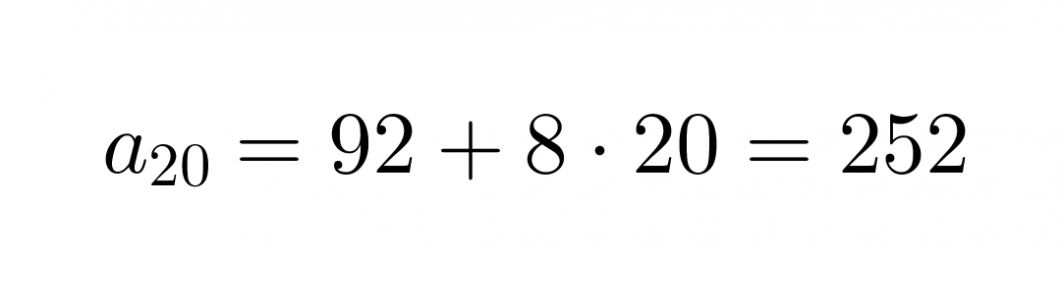
Klikkaa kuva suuremmaksi!
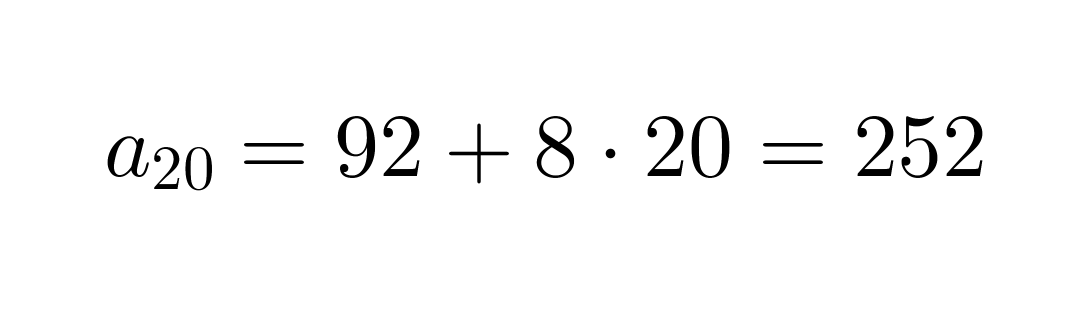
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Rahaa on säästössä 20 viikon kuluttua 252 €.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014