10. Geometrinen lukujono

Luku­jono 1, 2, 4, 8, 16, 32, … on esi­merk­ki ge­o­met­ri­ses­ta luku­jo­nos­ta. Sii­nä ku­kin ter­mi saa­daan ker­to­mal­la edel­li­nen lu­vul­la 2. Täl­lais­ta jo­noa, jos­sa ter­mi saa­daan edel­li­ses­tä ker­to­mal­la se sa­mal­la va­ki­ol­la, sa­no­taan ge­o­met­ri­sek­si luku­jo­nok­si.

Tar­kas­tel­laan ge­o­met­ri­sen luku­jo­non ylei­sen ter­min a_n esit­tä­mis­tä luku­jo­non en­sim­mäi­sen ter­min a₁ ja va­ki­on q avul­la

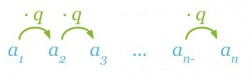
Klik­kaa kuva suu­rem­mak­si!

a₂ = a₁q

a₃ = a₂q = a₁qq = a₁q²

a₄ = a₃q = a₁qqq = a₁q³

a_n = a₁q^n-1

Esimerkki 1.

Bak­tee­rit li­sään­ty­vät ja­kau­tu­mal­la kah­tia. Eräi­tä bak­tee­re­ja on aluk­si 10 kpl ja nii­den luku­mää­rä kak­sin­ker­tais­tuu tun­nin vä­lein. Bak­tee­rin luku­mää­rää voi­daan ku­va­ta luku­jo­non avul­la

10, 20, 40, 80, 160, …

Ky­sees­sä on ge­o­met­ri­nen luku­jono, jon­ka en­sim­mäi­nen ter­mi on a₁ = 10 ja suh­de­luku q = 2.

a) Muo­dos­te­taan luku­jo­non ylei­nen ter­mi

a_n = 10 · 2^n-1

b) Las­ke­taan, pal­jon­ko bak­tee­rei­ta on 20 tun­nin ku­lut­tua

a₂₀ = 10 · 2^20-1 = 5 242 880

Esimerkki 2.

Heik­ki tal­let­ti ti­lil­leen 1500 €. Ti­lin vuo­tui­nen kor­ko oli 3,0 %, jo­ten jo­kai­se­na vuon­na tal­le­tus kas­vaa 1,03-ker­tai­sek­si. Ti­lil­lä ole­va raha­mää­rä voi­daan ku­va­ta ge­o­met­ri­se­na jo­no­na:

Klik­kaa kuva suu­rem­mak­si!

Luku­jo­non en­sim­mäi­nen ter­mi on a₁ = 1500 € · 1,03 = 1545 € ja suh­de­luku q = 1,03.

a) Muo­dos­te­taan luku­jo­non ylei­nen ter­mi:

a_n = 1545 € · 1,03^n-1.

b) Las­ke­taan, pal­jon­ko Hei­kil­lä on sääs­tö­jä 10 vuo­den ku­lut­tua:

a₁₀ = 1545 €  · 1,03^10-1 = 2015, 87 €