11. Yhtälöpari ja sen ratkaiseminen graafisesti
Esimerkki 1.
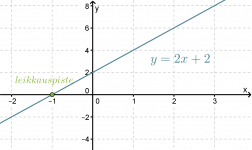
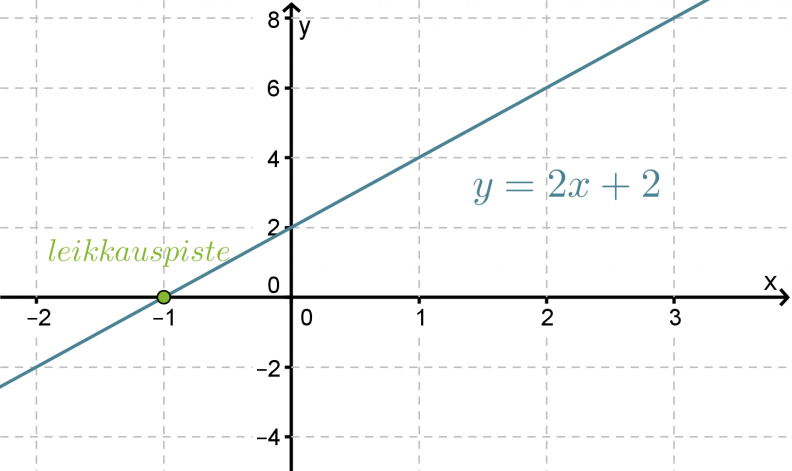
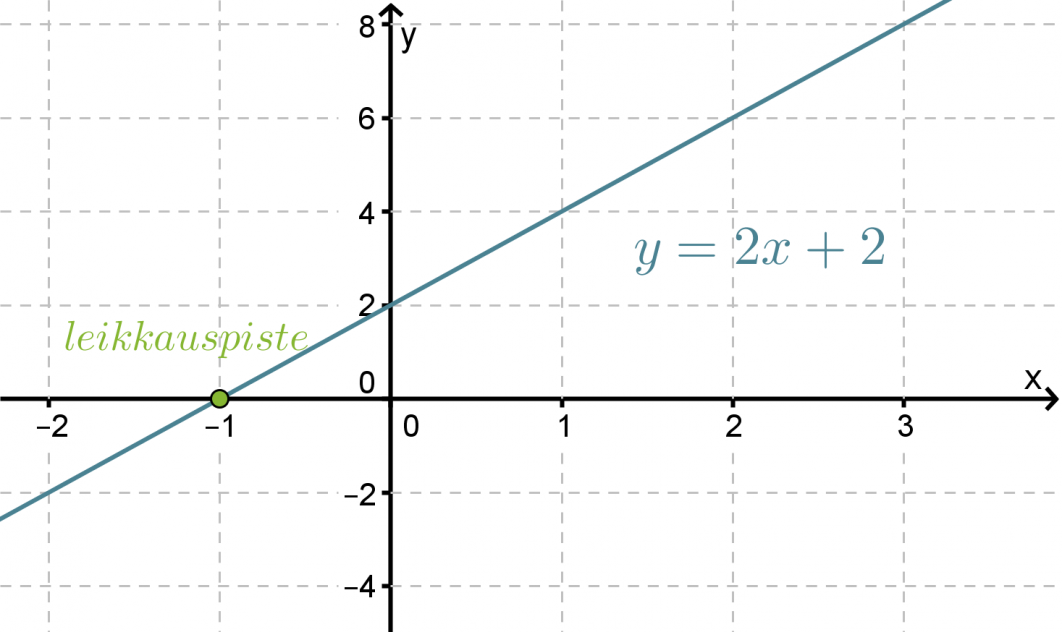
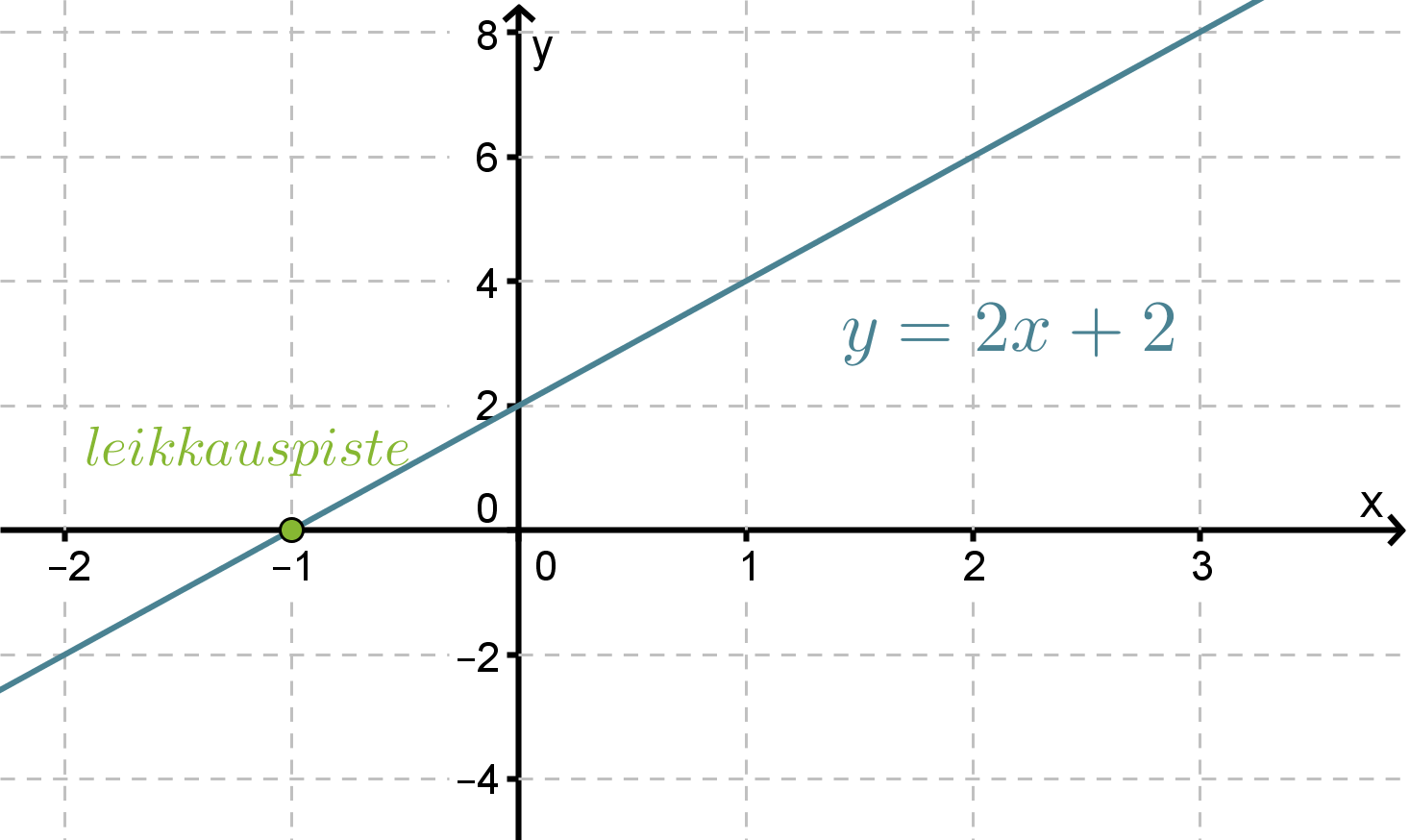
Määritetään suoran y = 2x + 2 ja x-akselin leikkauspiste graafisesti.
Klikkaa kuva suuremmaksi!
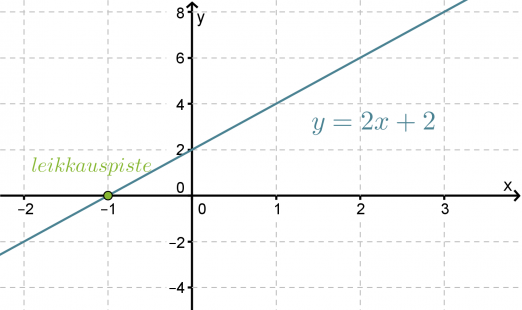
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kuvaajasta nähdään että suoran ja x-akselin leikkauspiste on x = -1.
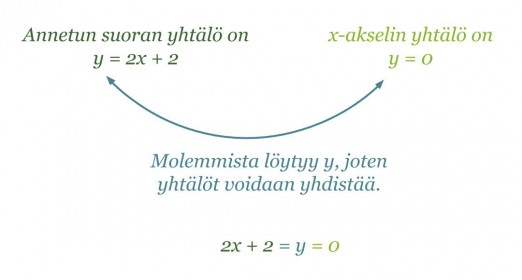
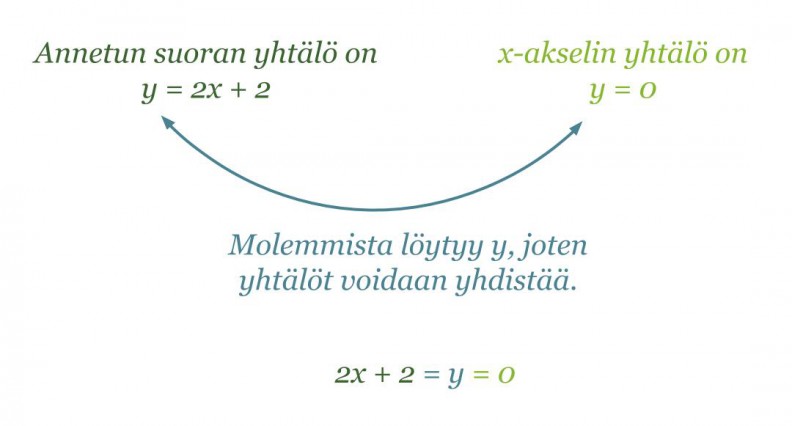
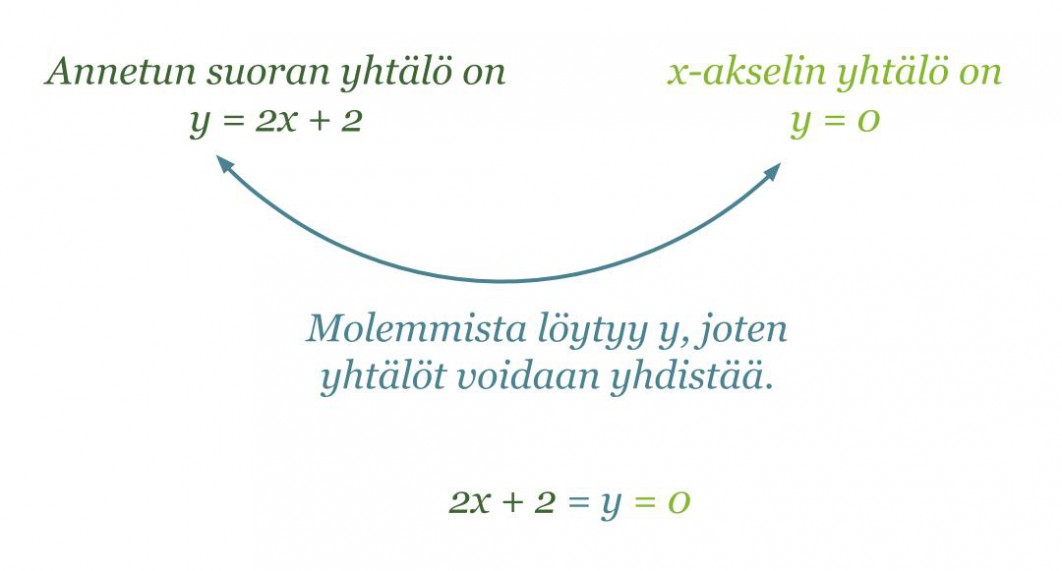
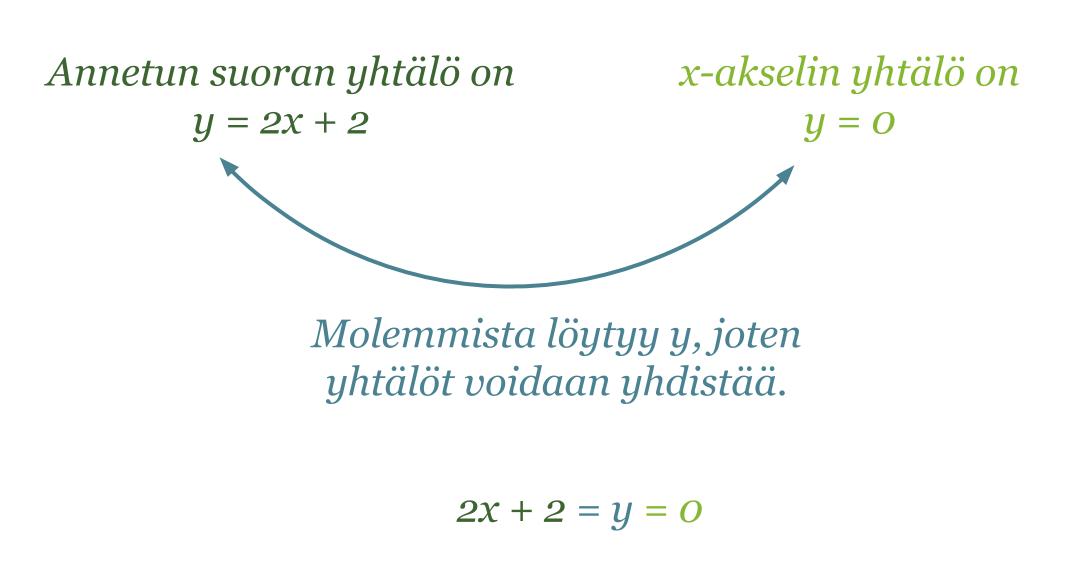
Laskennallisesti leikkauspiste löytyy ratkaisemalla yhtälö 2x + 2 = 0. Tutkitaan tarkemmin, miten yhtälö 2x + 2 = 0 on muodostunut.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kyseessä on kahden yhtälön yhdistäminen eli yhtälöpari, joka yleensä esitetään muodossa
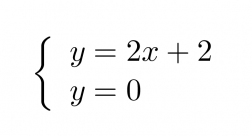
Klikkaa kuva suuremmaksi!
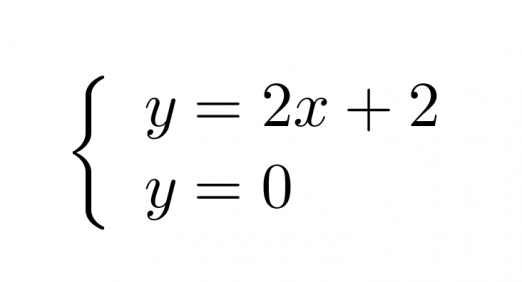
Klikkaa kuva suuremmaksi!
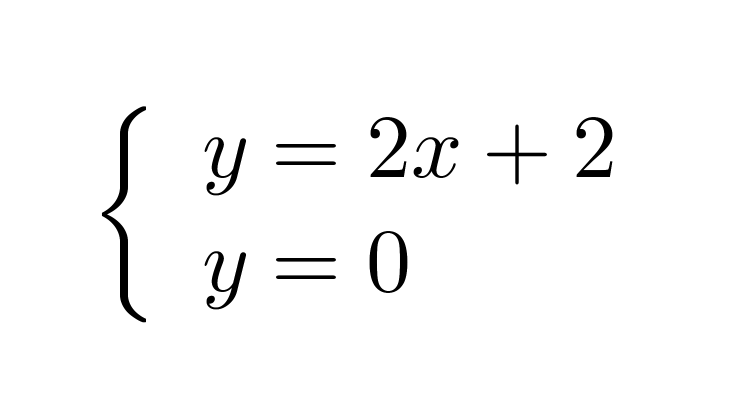
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kahden suoran leikkauspisteen etsiminen tarkoittaa siis kyseisten yhtälöiden muodostaman yhtälöparin ratkaisemista. Yhtälöparin ratkaisuna saadaan ne pisteet, jotka antava saman tuloksen sijoitettiinpa ne kumpaan yhtälöparin yhtälöön tahansa. Leikkauspisteiden koordinaattien määrittäminen graafisesti on aina yhtälöparin likimääräinen ratkaisu. Tarkat arvot muuttujille saadaan ainoastaan laskemalla.
Kaikilla yhtälöpareilla ei ole ratkaisua, joillakin voi niitä puolestaan olla äärettömän monta.
Jos kaksi suoraa
- leikkaavat toisensa, yhtälöparilla on yksi ratkaisu
- ovat yhdensuuntaiset, yhtälöparilla ei ole ratkaisua
- yhtyvät, yhtälöparilla on ääretön määrä ratkaisuja
Esimerkki 2.
Ratkaistaan yhtälöpari
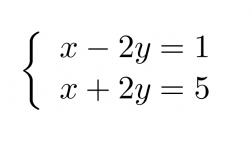
Klikkaa kuva suuremmaksi!
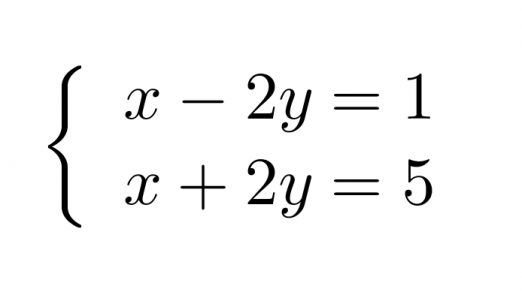
Klikkaa kuva suuremmaksi!
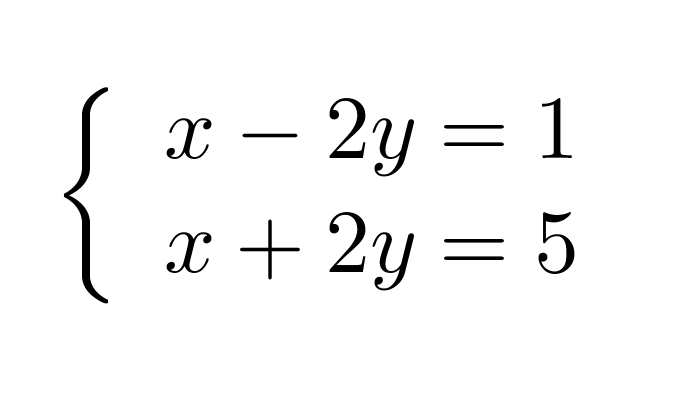
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
graafisesti.
Muutetaan yhtälöt ensin yleiseen muotoon.
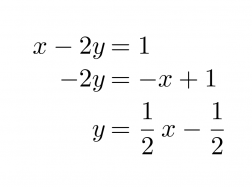
Klikkaa kuva suuremmaksi!
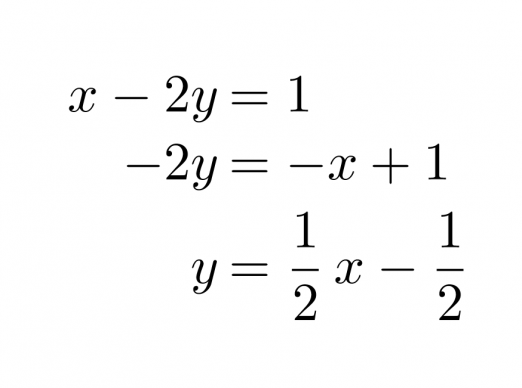
Klikkaa kuva suuremmaksi!
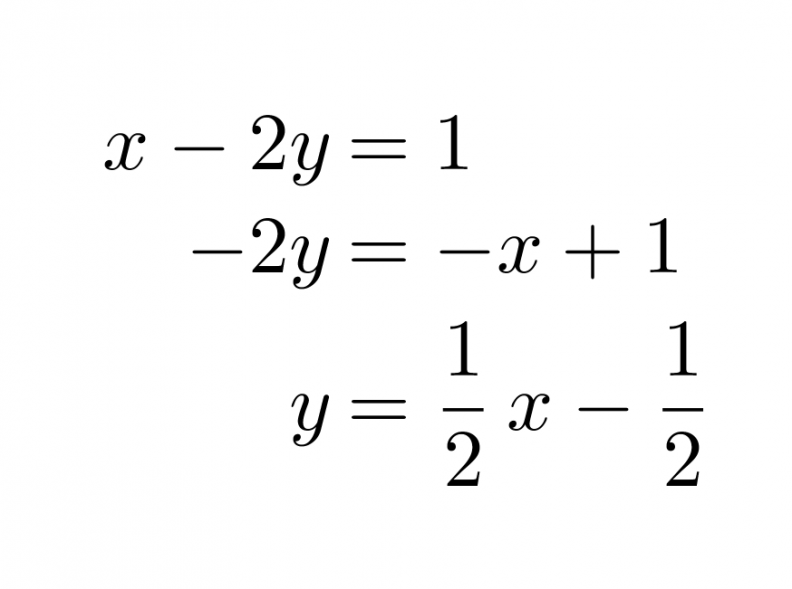
Klikkaa kuva suuremmaksi!
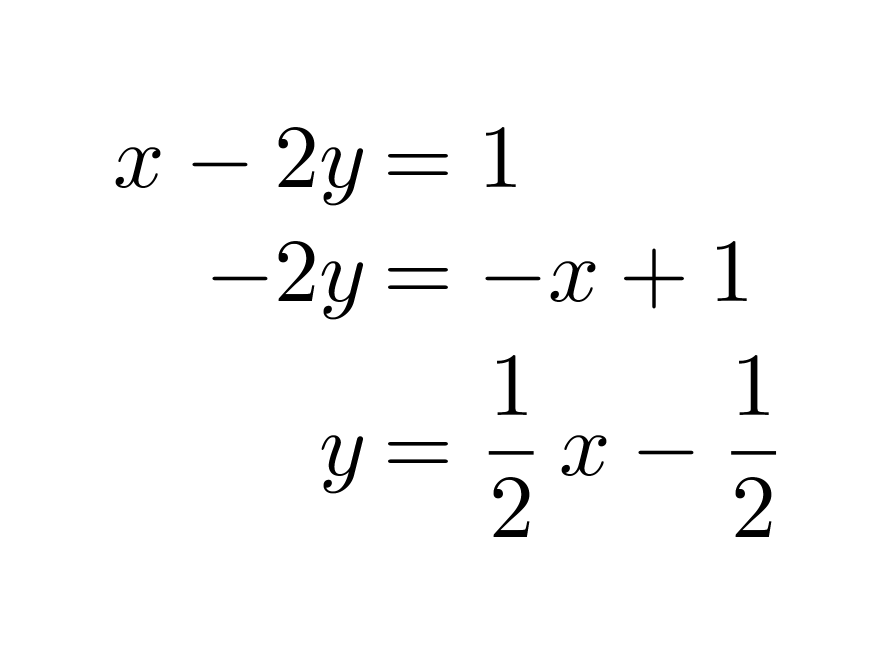
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
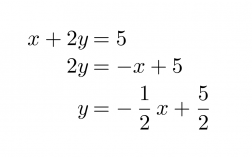
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
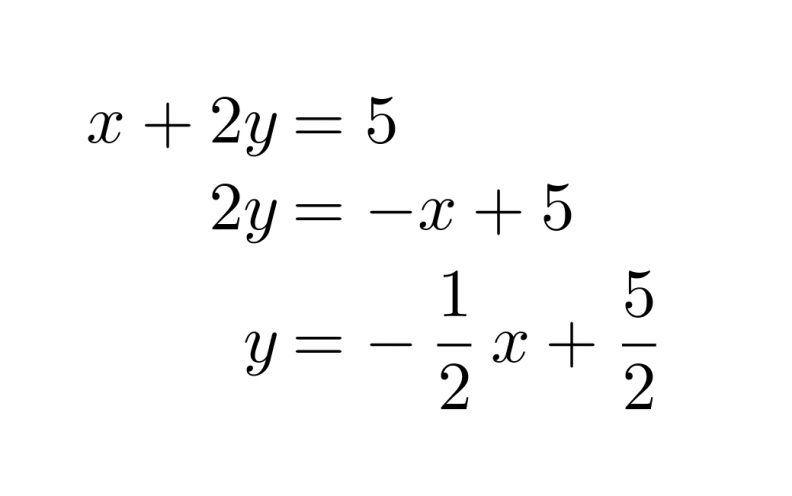
Klikkaa kuva suuremmaksi!
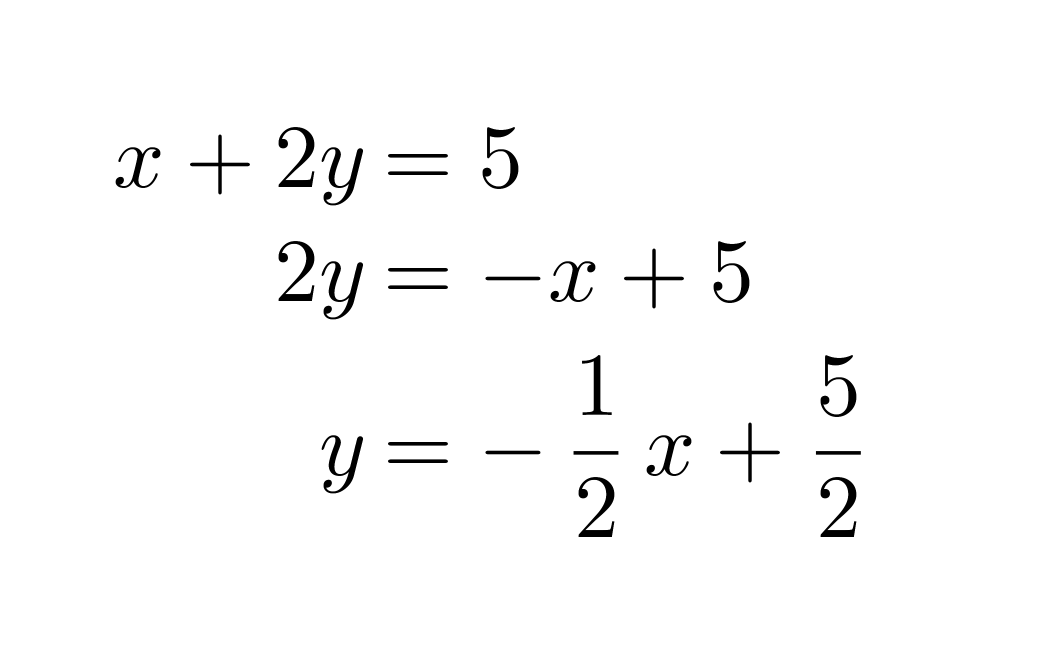
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
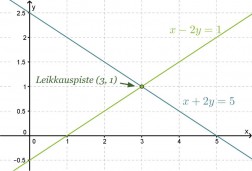
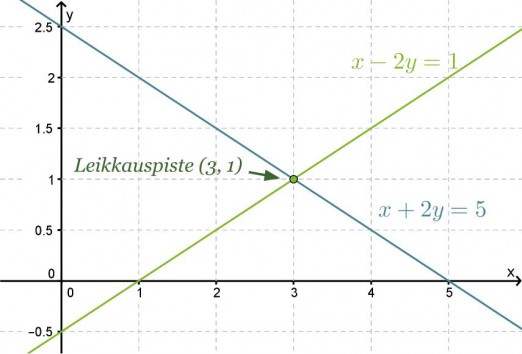
Piirretään suorat samaan koordinaatistoon ja määritetään niiden leikkauspiste.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Yhtälöparin ratkaisu on x = 3 ja y = 1.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014
Yhtälöparin graafinen ratkaisu