12. Yhtälöparin ratkaiseminen laskemalla
Yhtälöparissa on yleensä kaksi tuntematonta. Yhtälöparin laskennallisia ratkaisutapoja on useita. Yhteistä kaikille tavoille kuitenkin on, että toinen tuntemattomista poistetaan. Jäljelle pyritään saamaan ainoastaan yksi yhtälö, jossa on yksi muuttuja. Tämä yhtälö ratkaistaan tavallisia yhtälön ratkaisusääntöjä noudattaen. Kun saatu ratkaisu sijoitetaan jompaankumpaan alkuperäisen yhtälöparin yhtälöistä, löydetään toinen tuntemattomista.
Joskus helpoin tapa yhtälön toisen muuttujan eliminoimiseen on yhtälöiden laskeminen puolittain yhteen. Mitä enemmän yhtälöparin ratkaisemista harjoittelee, sitä nopeammin oppii löytämään tehokkaimman ratkaisukeinon.
Yhtälöparin ratkaiseminen eliminoimalla
- Siirretään tuntemattoman sisältävät termit yhtälön vasemmalle puolelle ja vakiot oikealle puolelle
- Kerrotaan toinen tai molemmat yhtälöt tarvittaessa siten, että toiselle muuttujista muodostuu muuten sama, mutta vastakkaismerkkinen kerroin
- Lasketaan yhtälöt puolittain yhteen
- Ratkaistaan jäljelle jäänyt yhtälö
- Toistetaan sama toiselle muuttujalle
- Tarkistetaan ratkaisut sijoittamalla.
Esimerkki 1.
Ratkaistaan yhtälöpari sijoitusmenetelmällä.
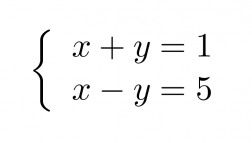
Klikkaa kuva suuremmaksi!
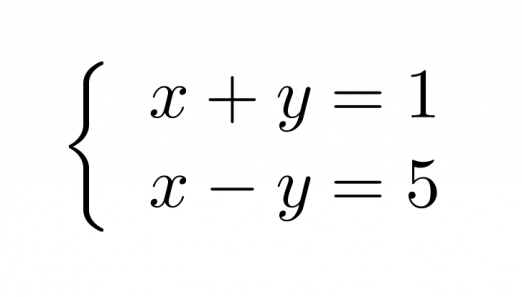
Klikkaa kuva suuremmaksi!
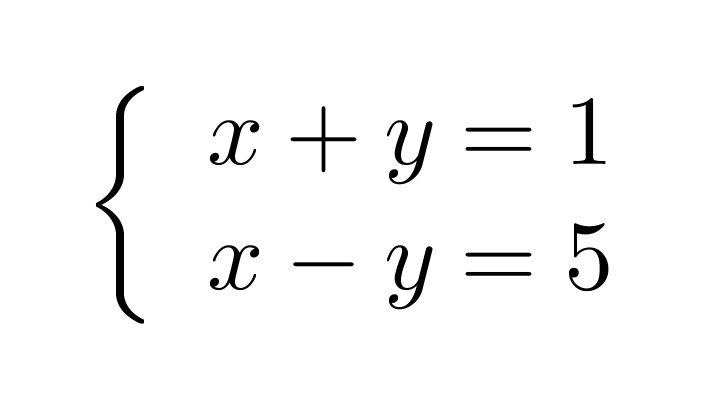
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaistaan alemmasta yhtälöstä y ja sijoitetaan y:n arvo ylempään yhtälöön.

Klikkaa kuva suuremmaksi!
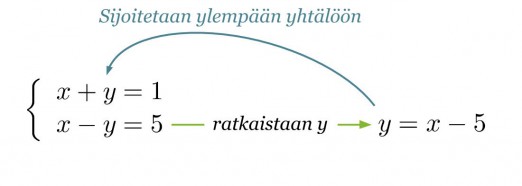
Klikkaa kuva suuremmaksi!
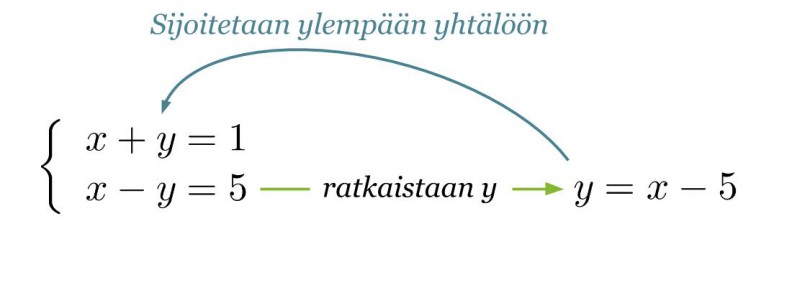
Klikkaa kuva suuremmaksi!
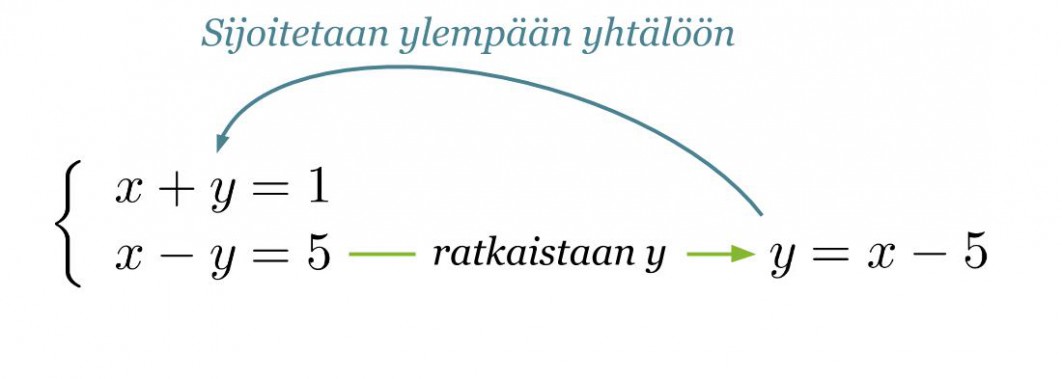
Klikkaa kuva suuremmaksi!
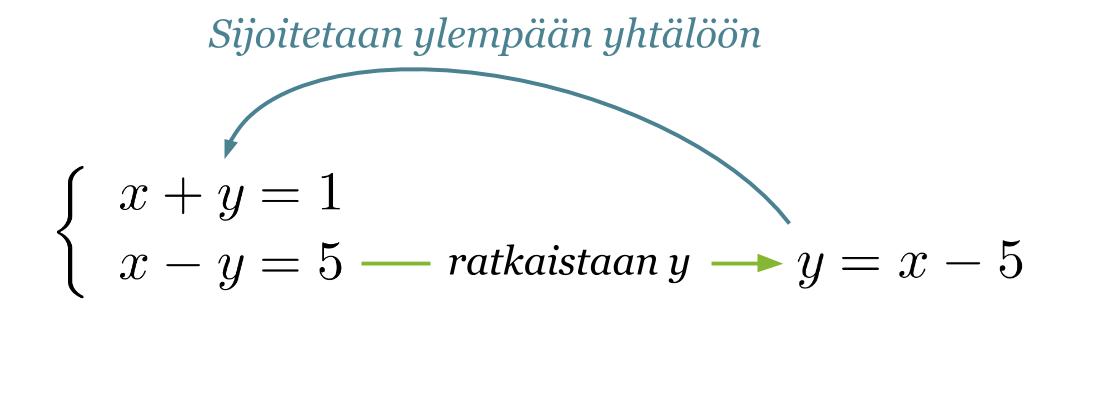
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Saadaan yhtälö, jossa on muuttujana ainoastaan x.
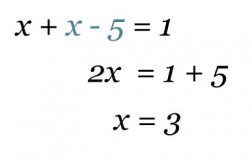
Klikkaa kuva suuremmaksi!
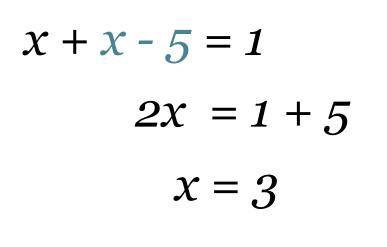
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Sijoitetaan saatu arvo x = 3 yhtälöön y = x – 5, josta ratkaistaan y = -2.
Tarkistus:
Sijoitetaan arvot yhtälöihin ja katsotaan toteutuvatko ne:
3 + (-2) = 1 ja 3 – (-2) = 5
Molemmat yhtälöt pitävät paikkaansa, joten ratkaisut ovat oikein.
Vastaus: x = 3 ja y = -2
Esimerkki 2.
Ratkaistaan yhtälöpari eliminoimalla.
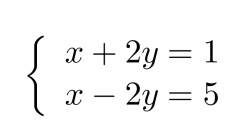
Klikkaa kuva suuremmaksi!
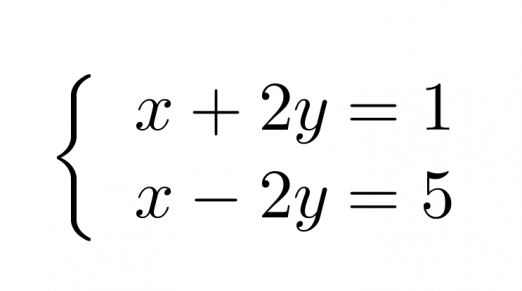
Klikkaa kuva suuremmaksi!
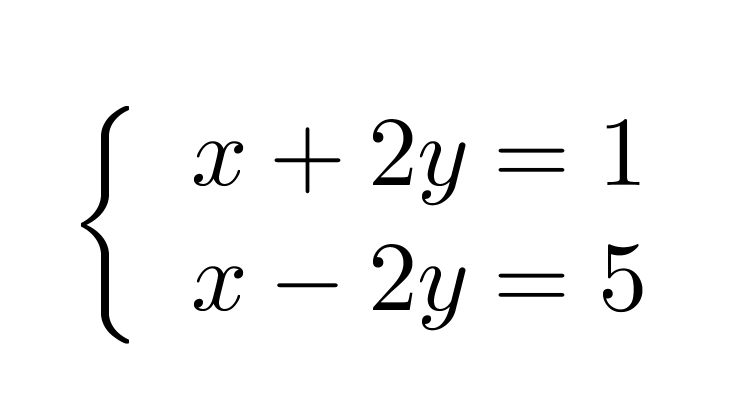
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Eliminoidaan yhtälöstä muuttujat y. Yhtälöissä on sama määrä, mutta vastakkaismerkkisiä muuttujia y. Laskemalla yhtälöt puolittain yhteen, sievenevät muuttujat y pois.
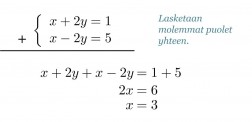
Klikkaa kuva suuremmaksi!
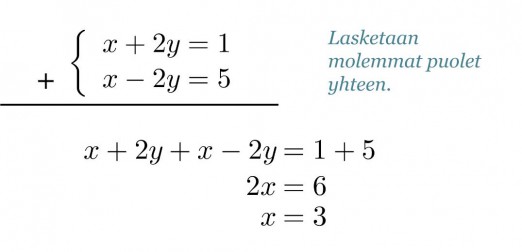
Klikkaa kuva suuremmaksi!
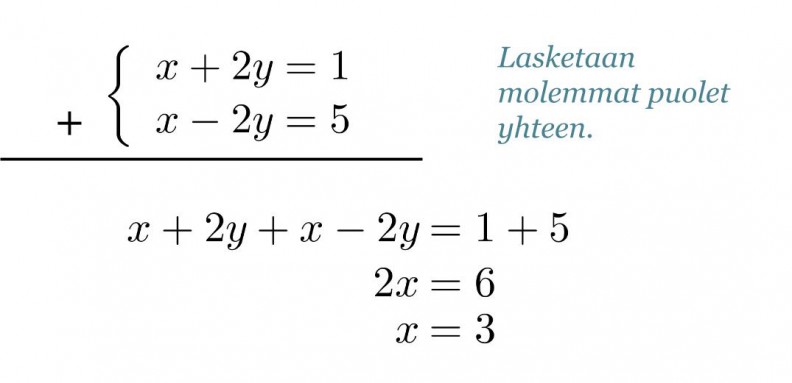
Klikkaa kuva suuremmaksi!
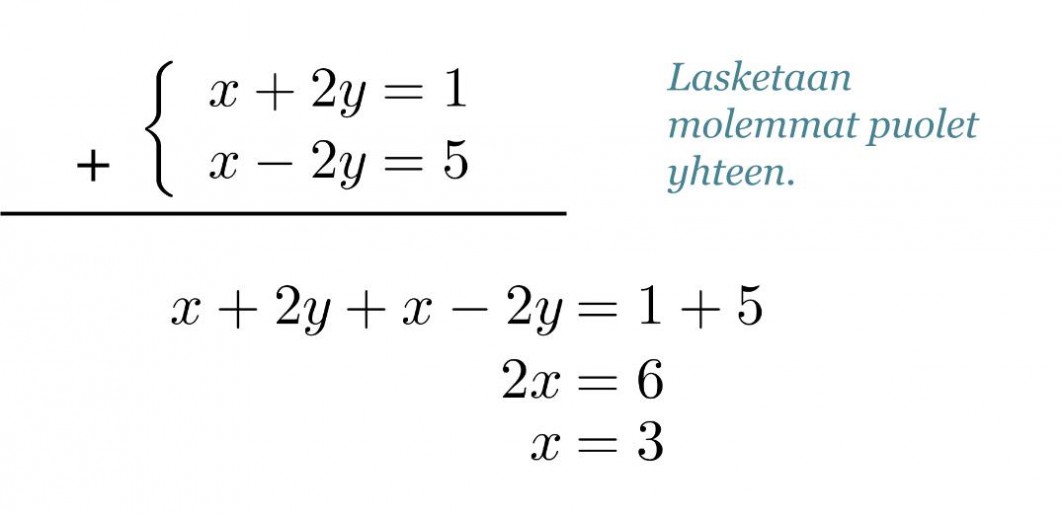
Klikkaa kuva suuremmaksi!
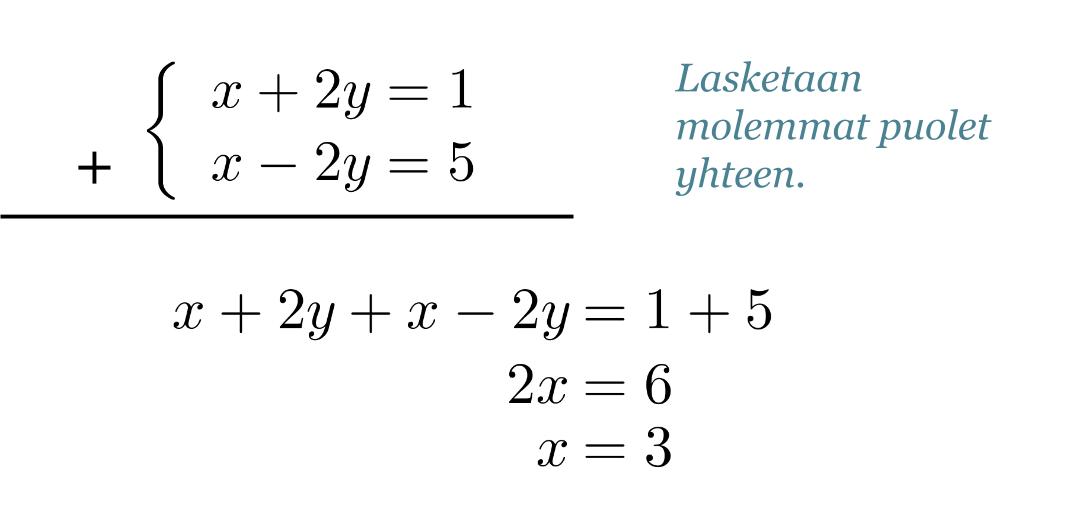
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Eliminoidaan yhtälöstä seuraavaksi muuttujat x. Jos ylempi yhtälöistä kerrotaan luvulla –1 ja lasketaan yhtälöt yhteen, sievenevät muuttujat x pois.
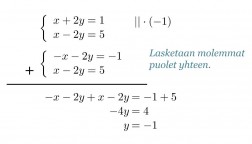
Klikkaa kuva suuremmaksi!
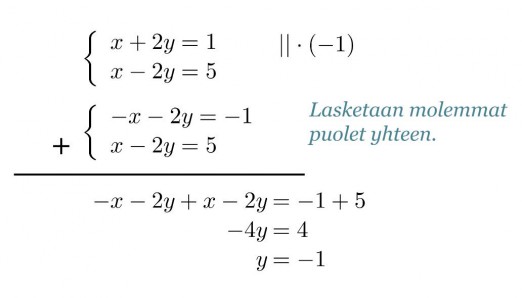
Klikkaa kuva suuremmaksi!
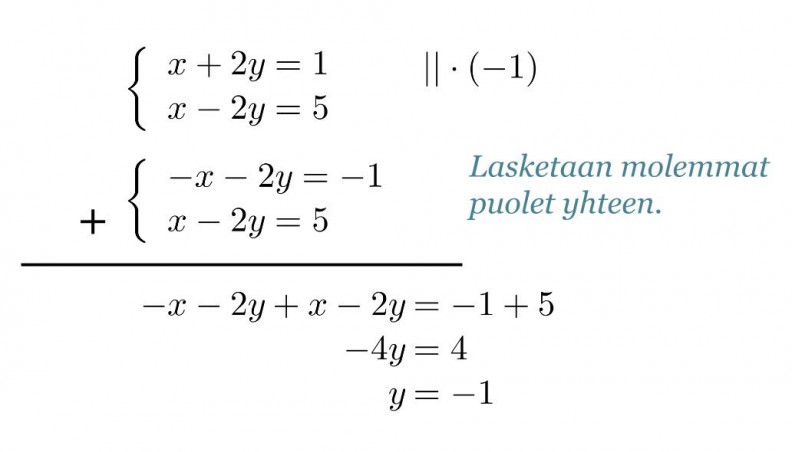
Klikkaa kuva suuremmaksi!
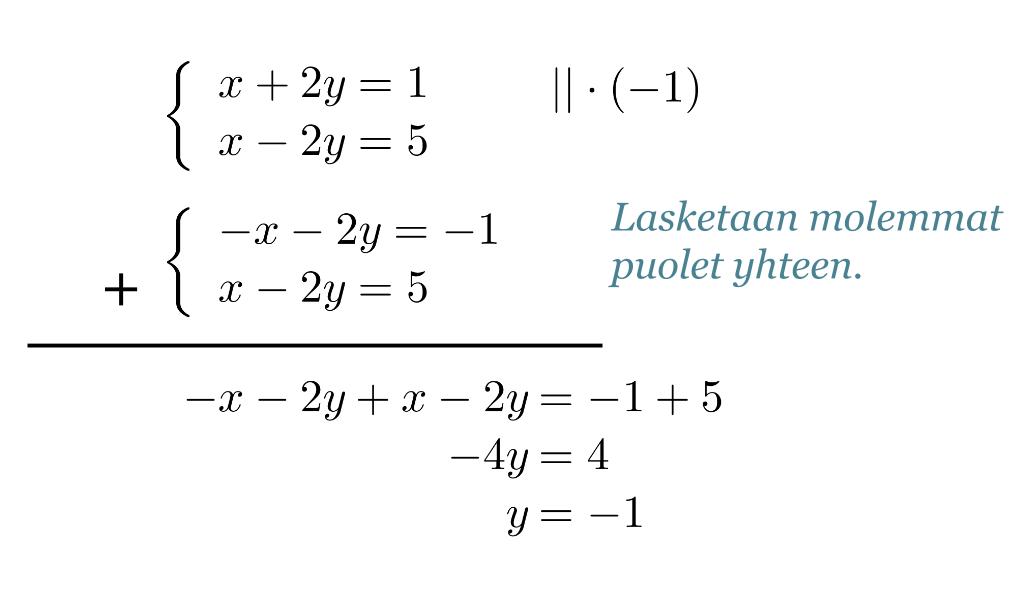
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: x = 3 ja y = -1.
Esimerkki 3.
Ratkaistaan yhtälöpari.
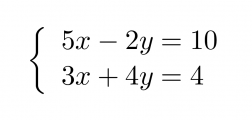
Klikkaa kuva suuremmaksi!
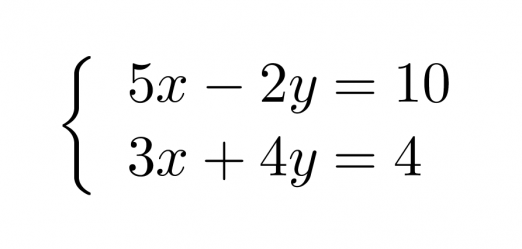
Klikkaa kuva suuremmaksi!
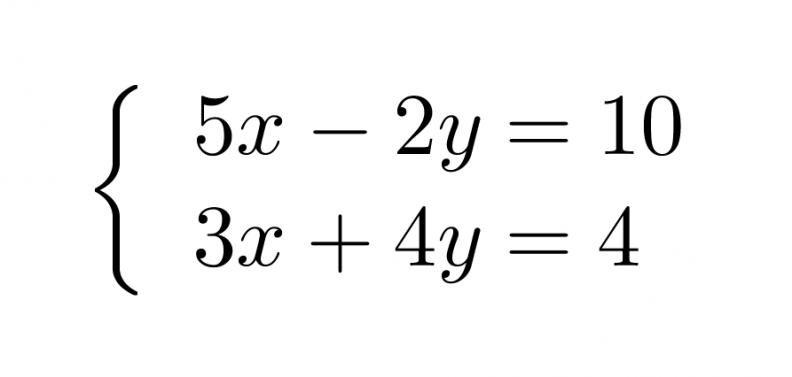
Klikkaa kuva suuremmaksi!
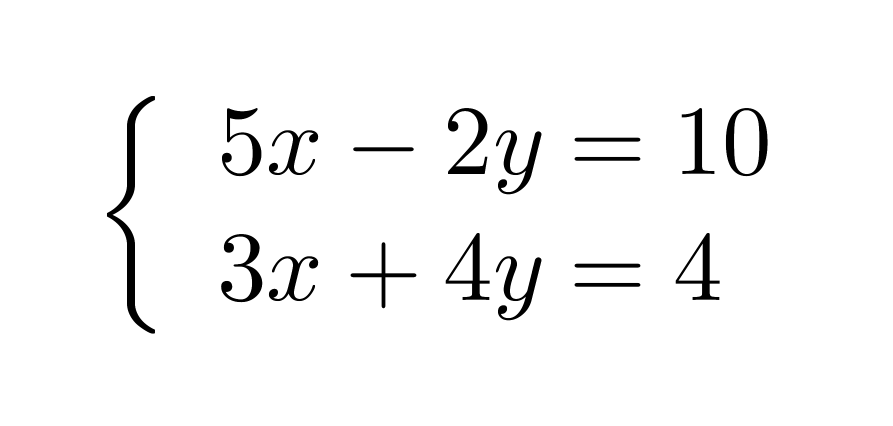
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Yhtälöihin saadaan sama määrä, mutta vastakkaismerkkisiä, muuttujia y, jos ylempi yhtälö kerrotaan kahdella.

Klikkaa kuva suuremmaksi!
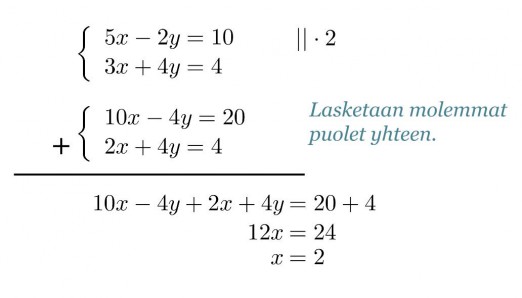
Klikkaa kuva suuremmaksi!
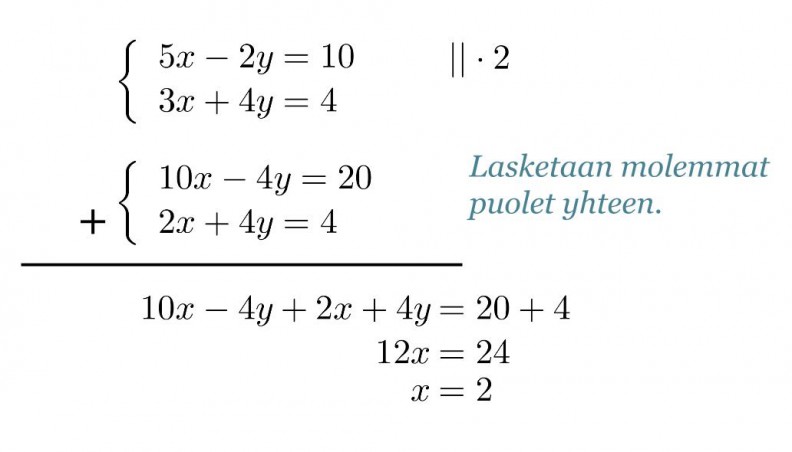
Klikkaa kuva suuremmaksi!
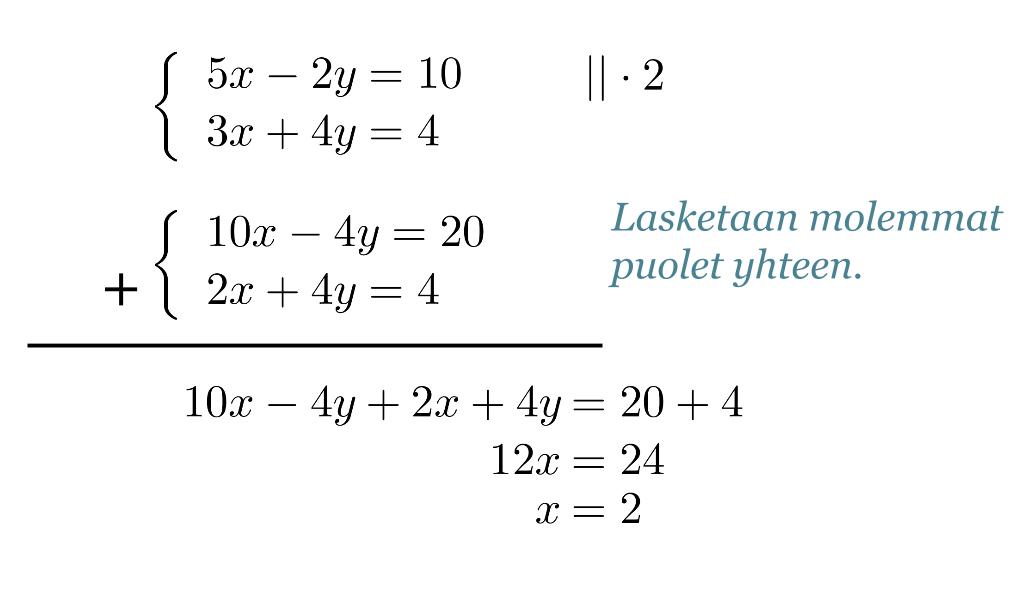
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Sijoitetaan saatu x:n arvo ylempään yhtälöön ja ratkaistaan siitä y.
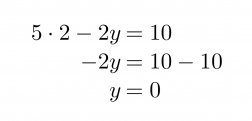
Klikkaa kuva suuremmaksi!
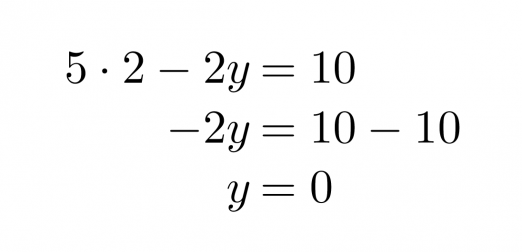
Klikkaa kuva suuremmaksi!
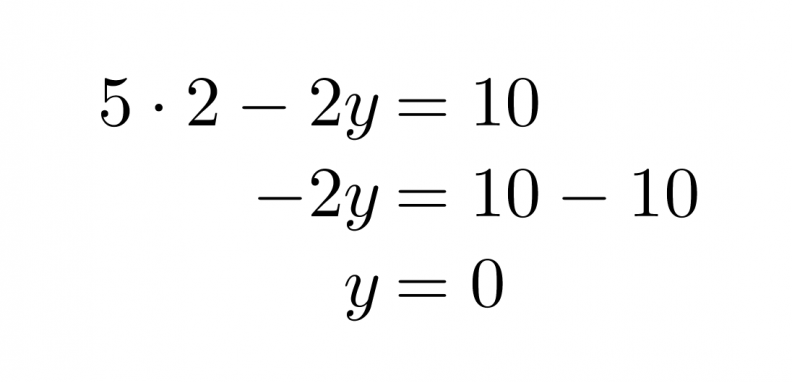
Klikkaa kuva suuremmaksi!
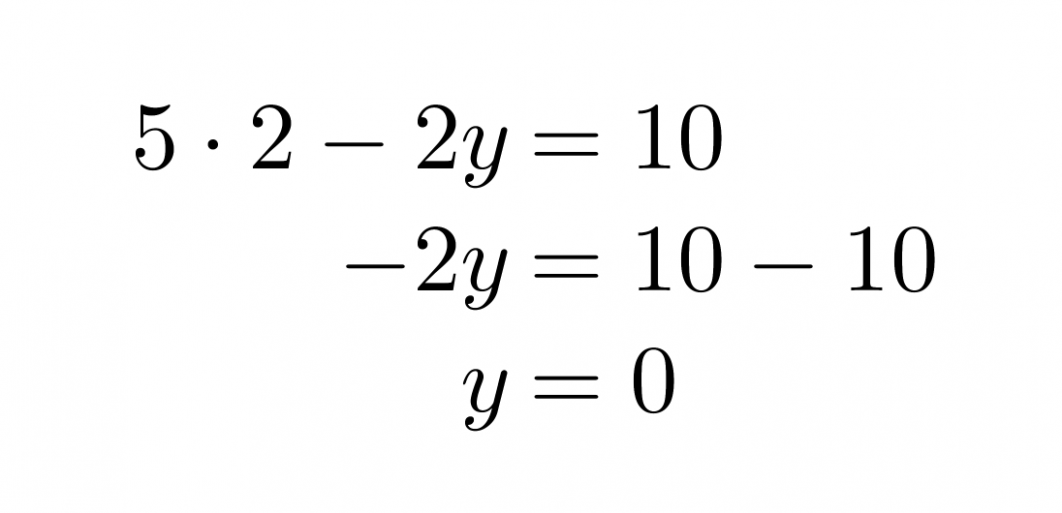
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: x = 2 ja y = 0.
Huom! Esimerkin 3 yhtälöparin ratkaisemisessa käytettiin sekä sijoitus- että eliminointimenetelmää.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014
Yhtälöparin ratkaiseminen sijoitusmenetelmällä