13. Yhtälöparin soveltaminen
Yhtälöparin käyttö on hyödyllistä useissa matemaattisissa ongelmissa. Jos jokin voidaan laskea kahdella eri tavalla, on se selvä vihje, että ongelma ratkeaa yhtälöparin avulla. Sovelluksissa merkitään usein toista muuttujaa x:llä ja toista y:llä.
Esimerkki 1.
Pitopalvelu veloittaa lasten ruoka-annoksesta 5,50 € ja aikuisten annoksesta 13,20 €. Juhlassa ruokaa menee yhteensä 130 annosta ja ruoka-annokset maksavat yhteensä 1500,40 €. Moniko saa lasten annoksen, entä aikuisten annoksen?
Ratkaisu:
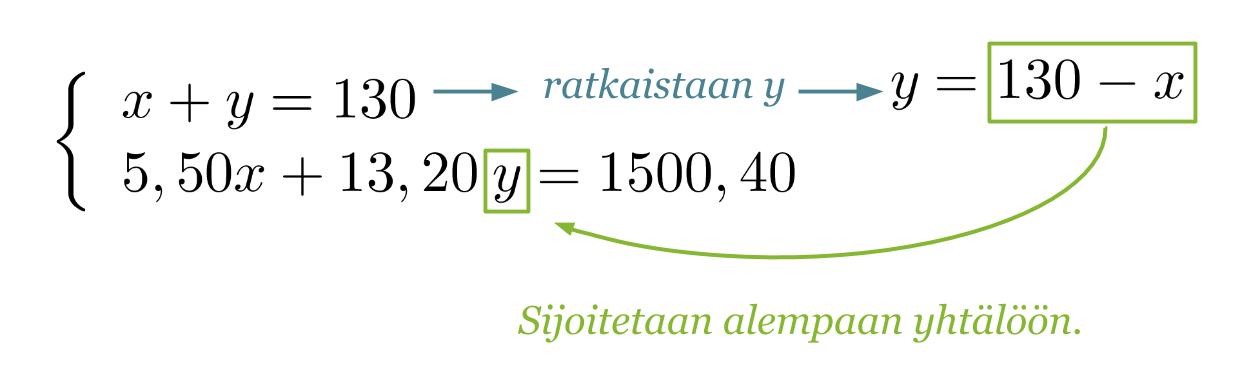
Olkoon lasten annosten lukumäärä x ja aikuisten y. Tietojen pohjalta voidaan muodostaa yhtälöpari.
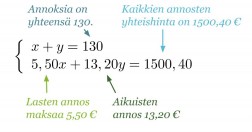
Klikkaa kuva suuremmaksi!
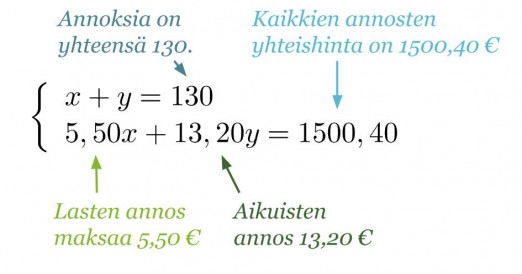
Klikkaa kuva suuremmaksi!
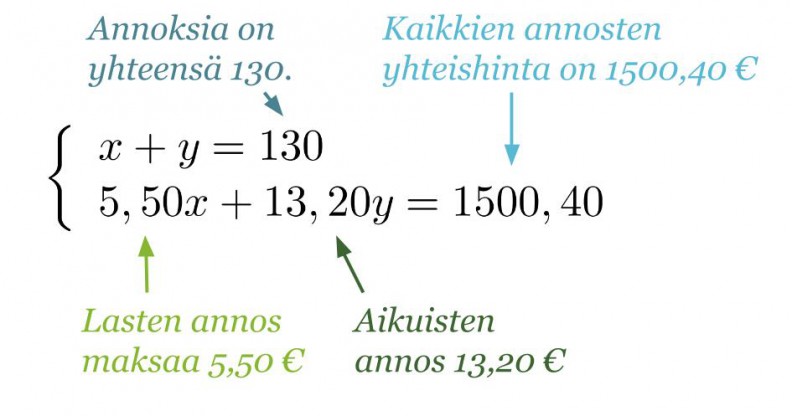
Klikkaa kuva suuremmaksi!
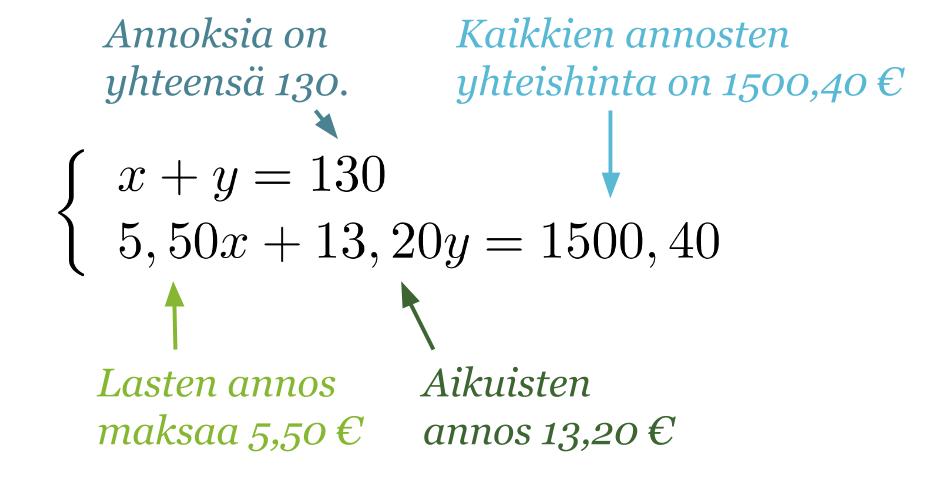
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
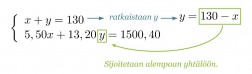
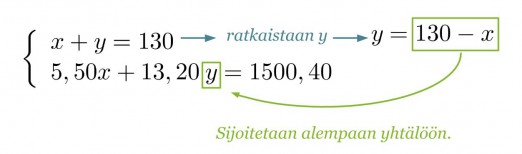
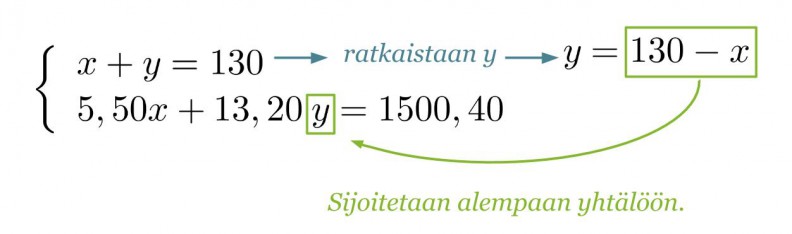
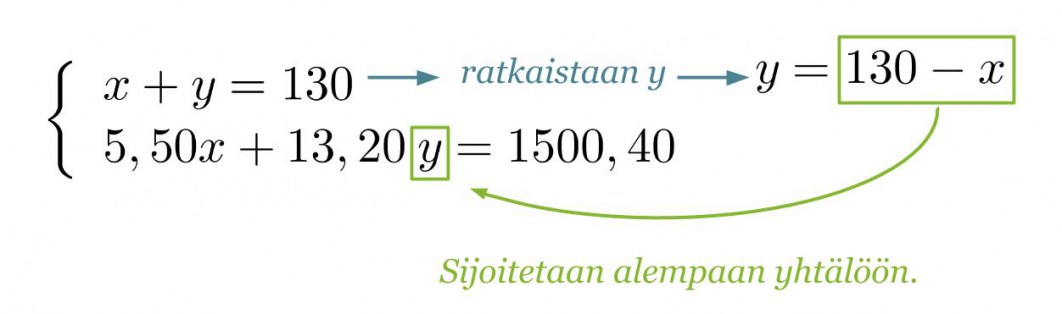
Ratkaistaan yhtälöpari sijoitusmenetelmällä.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
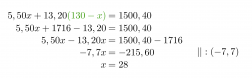
Klikkaa kuva suuremmaksi!
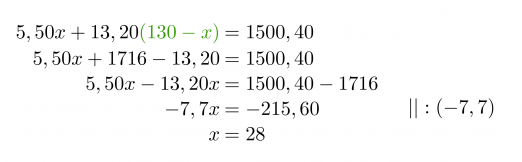
Klikkaa kuva suuremmaksi!
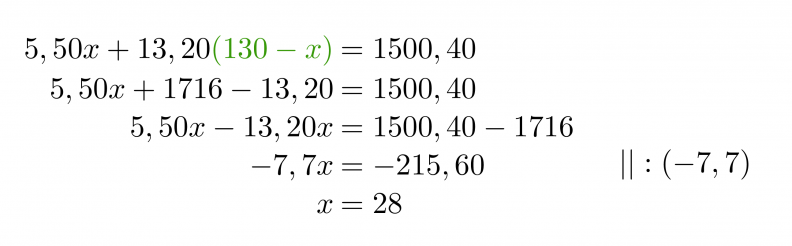
Klikkaa kuva suuremmaksi!
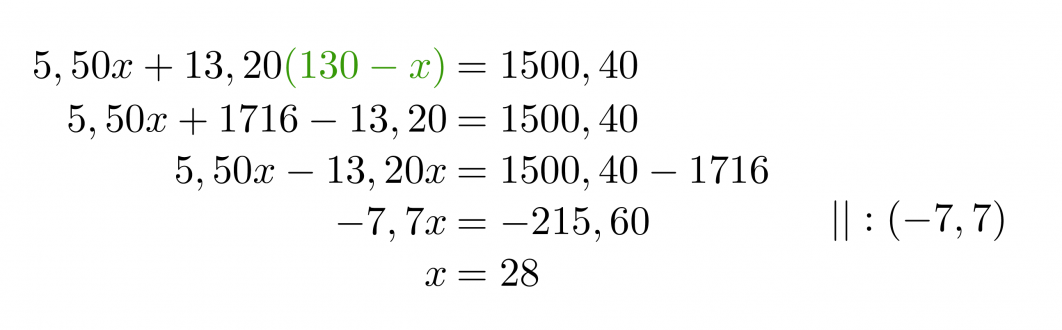
Klikkaa kuva suuremmaksi!
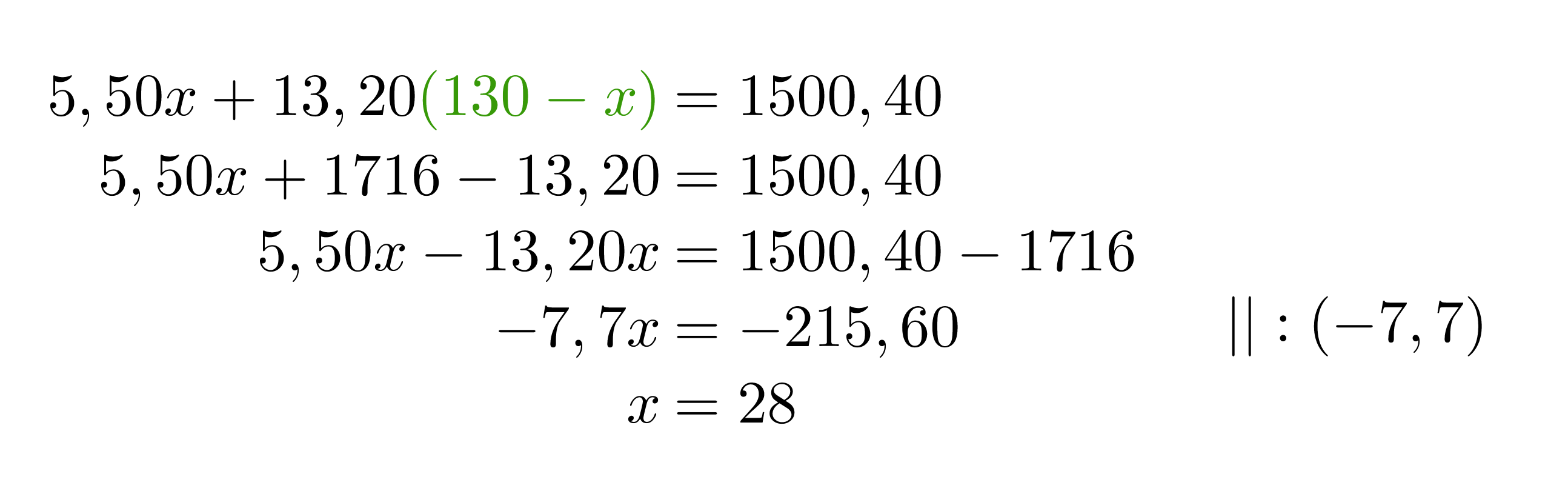
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Sijoitetaan saatu x:n ratkaisu y:n yhtälöön.
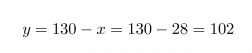
Klikkaa kuva suuremmaksi!
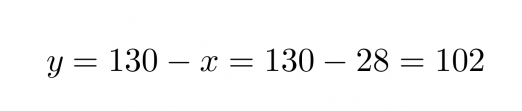
Klikkaa kuva suuremmaksi!
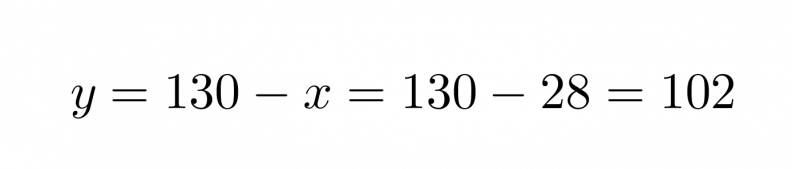
Klikkaa kuva suuremmaksi!
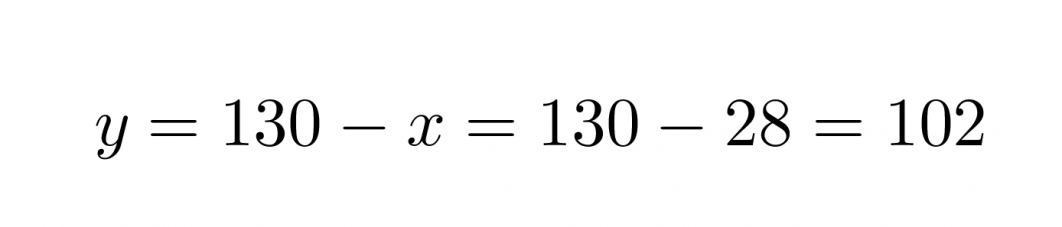
Klikkaa kuva suuremmaksi!
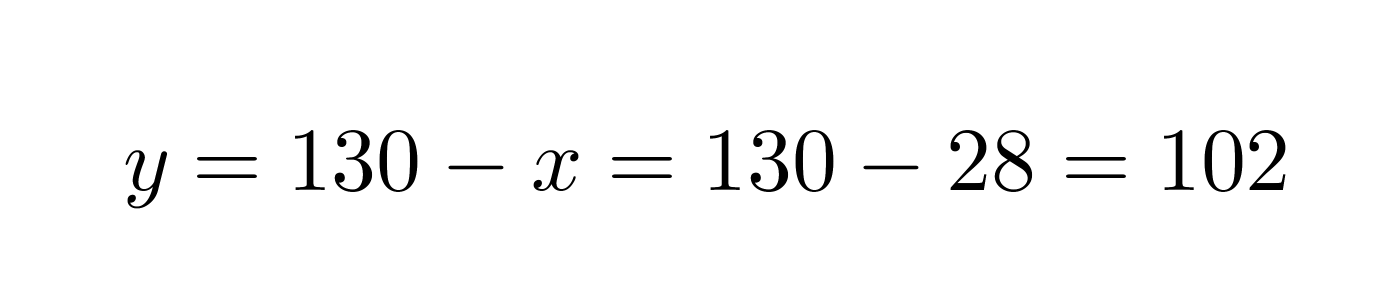
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Lasten annoksia on 28 ja aikuisten 102.
Esimerkki 2.
Mehutiivistettä ja vettä on sekoitettava suhteessa 1 : 9. Mehua tarvitaan syntymäpäiväjuhlille 30 litraa. Paljonko tarvitaan mehutiivistettä ja paljonko vettä?
Ratkaisu:
Merkitään mehutiivisteen määrä x:llä, veden määrä y:llä ja muodostetaan yhtälöpari.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Muutetaan sekoitussuhdetta kuvaava yhtälö toiseen muotoon ja sijoitetaan saatu y:n lauseke ylempään yhtälön.
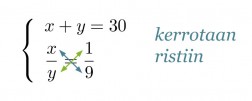
Klikkaa kuva suuremmaksi!
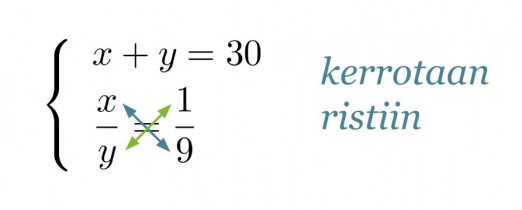
Klikkaa kuva suuremmaksi!
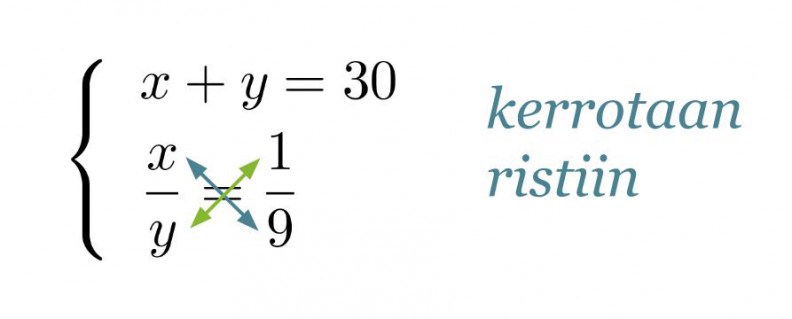
Klikkaa kuva suuremmaksi!
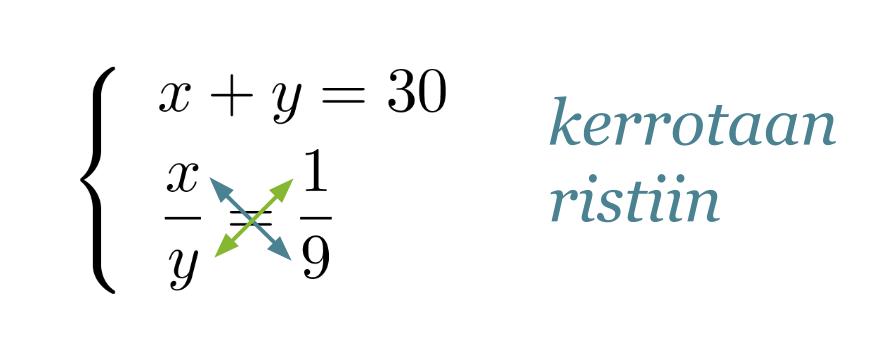
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
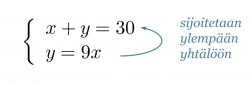
Klikkaa kuva suuremmaksi!
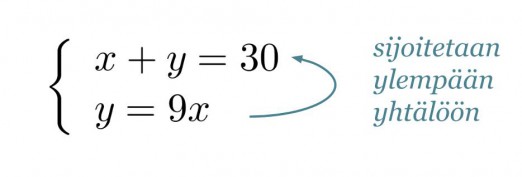
Klikkaa kuva suuremmaksi!
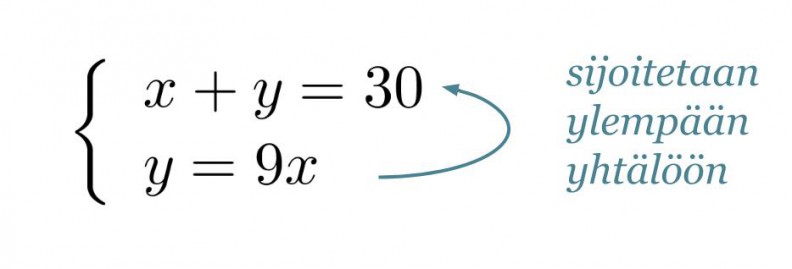
Klikkaa kuva suuremmaksi!
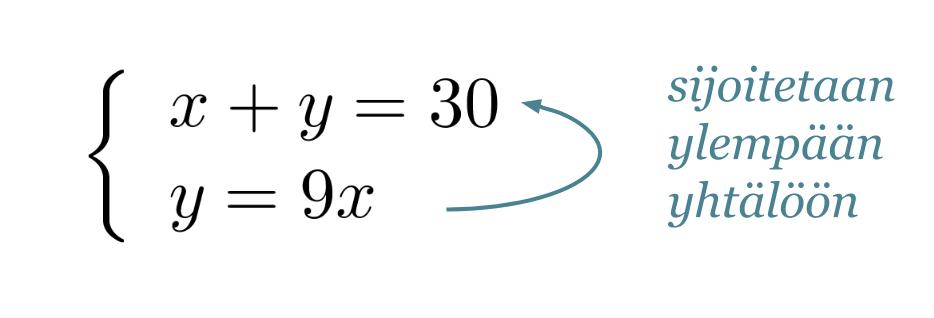
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
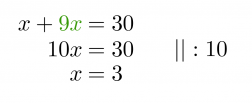
Klikkaa kuva suuremmaksi!
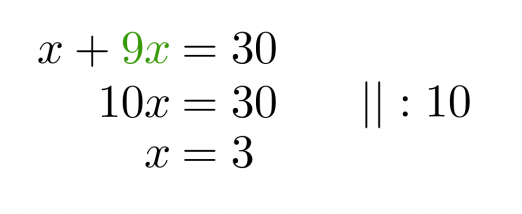
Klikkaa kuva suuremmaksi!
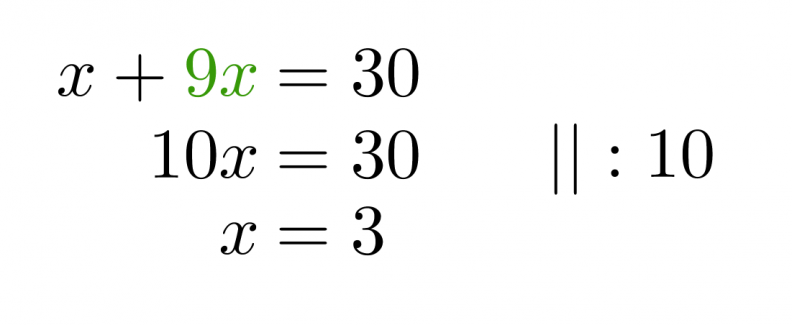
Klikkaa kuva suuremmaksi!
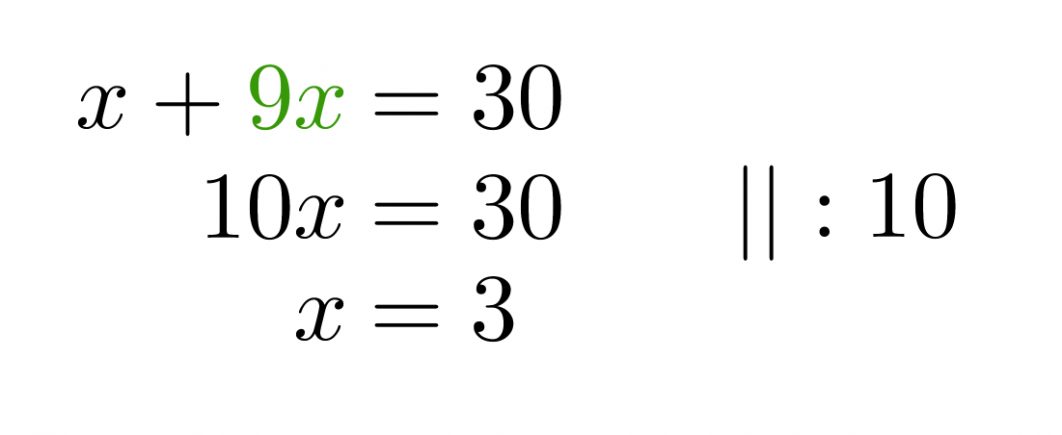
Klikkaa kuva suuremmaksi!
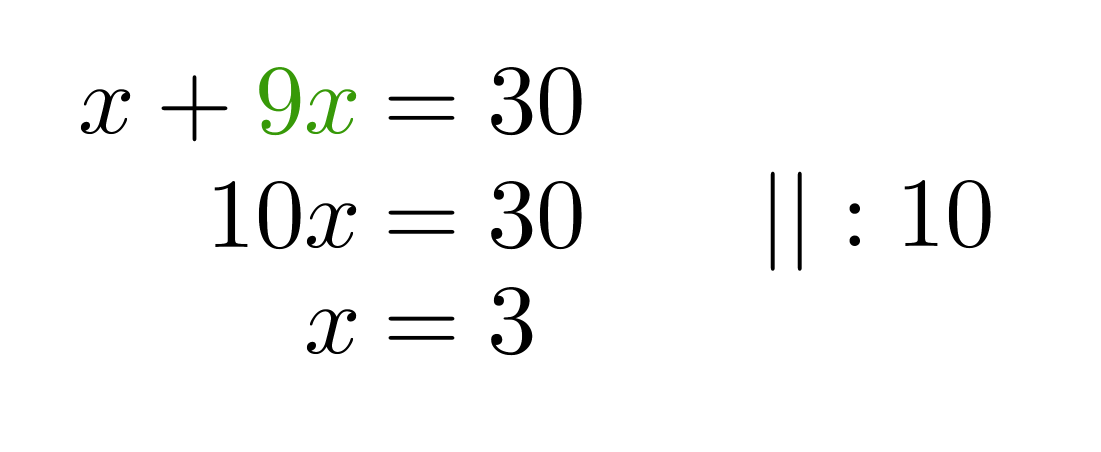
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Sijoitetaan saatu x:n ratkaisu y:n yhtälöön.
y = 9x = 9 · 3 = 27
Vastaus: Mehutiivistettä tarvitaan 3 litraa ja vettä 27 litraa.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014