14. Epäyhtälön ratkaiseminen graafisesti
Esimerkki 1.
Ratkaistaan epäyhtälö −9x + 16 ≥ −x ja havainnollistetaan ratkaisua lukusuoralla.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Epäyhtälö siis toteutuu, kun x on esimerkiksi 1, -3 tai vaikka -4,456. Ratkaisujen suurta määrää on helppo havainnollistaa lukusuoralla.

Klikkaa kuva suuremmaksi!
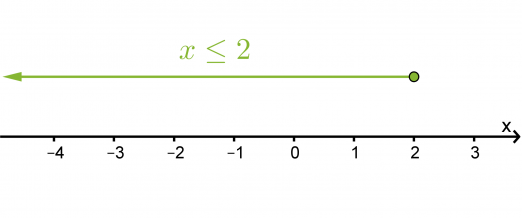
Klikkaa kuva suuremmaksi!
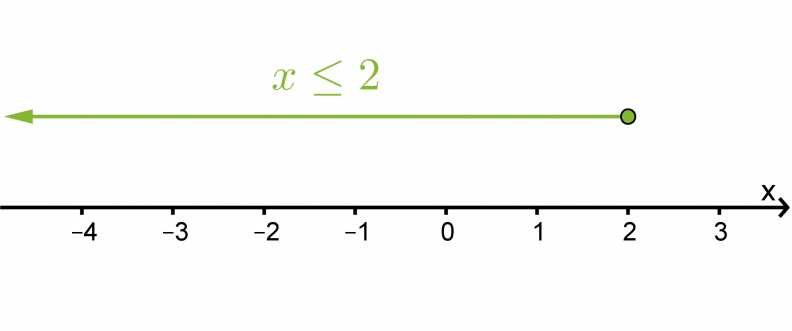
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Epäyhtälö on kyseessä silloin kun yhtälössä yhtäsuuruusmerkin tilalla on jokin epäyhtälöä kuvaavista merkeistä.
Epäyhtälöiden merkit
≠ eri suuri kuin
< pienempi kuin
> suurempi kuin
≤ pienempi tai yhtä suuri kuin
≥ suurempi tai yhtä suuri kuin
Epäyhtälöitä voidaan havainnollistaa kuvaajien avulla samaan tapaan kuin funktioita ja yhtälöitä. Epäyhtälötarkasteluja on aikaisemmin tehty pelkästään lukusuoralla. Lukusuora ei kuitenkaan sovellu kuin x– ja y-akselien suuntaisten epäyhtälöiden havainnollistamiseen. Laajempia tarkasteluja voidaan suorittaa koordinaatistossa, jossa voidaan havainnollistaa myös kahden muuttuja epäyhtälöitä.
Esimerkki 1.
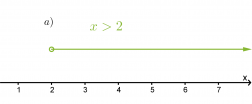
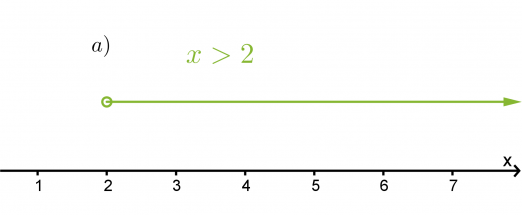
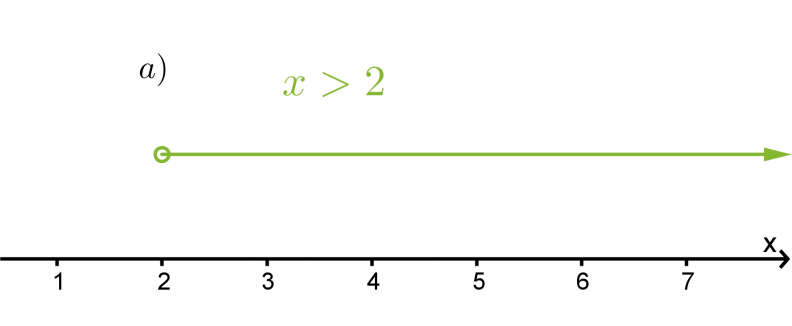
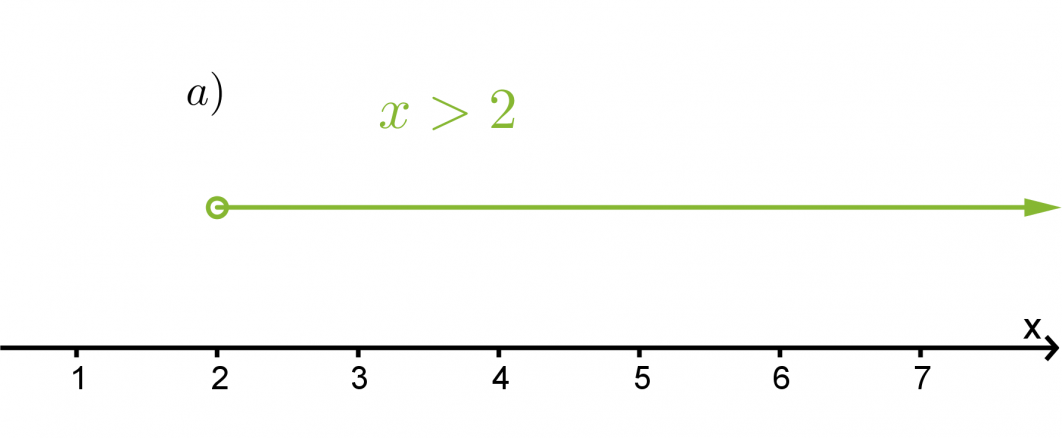
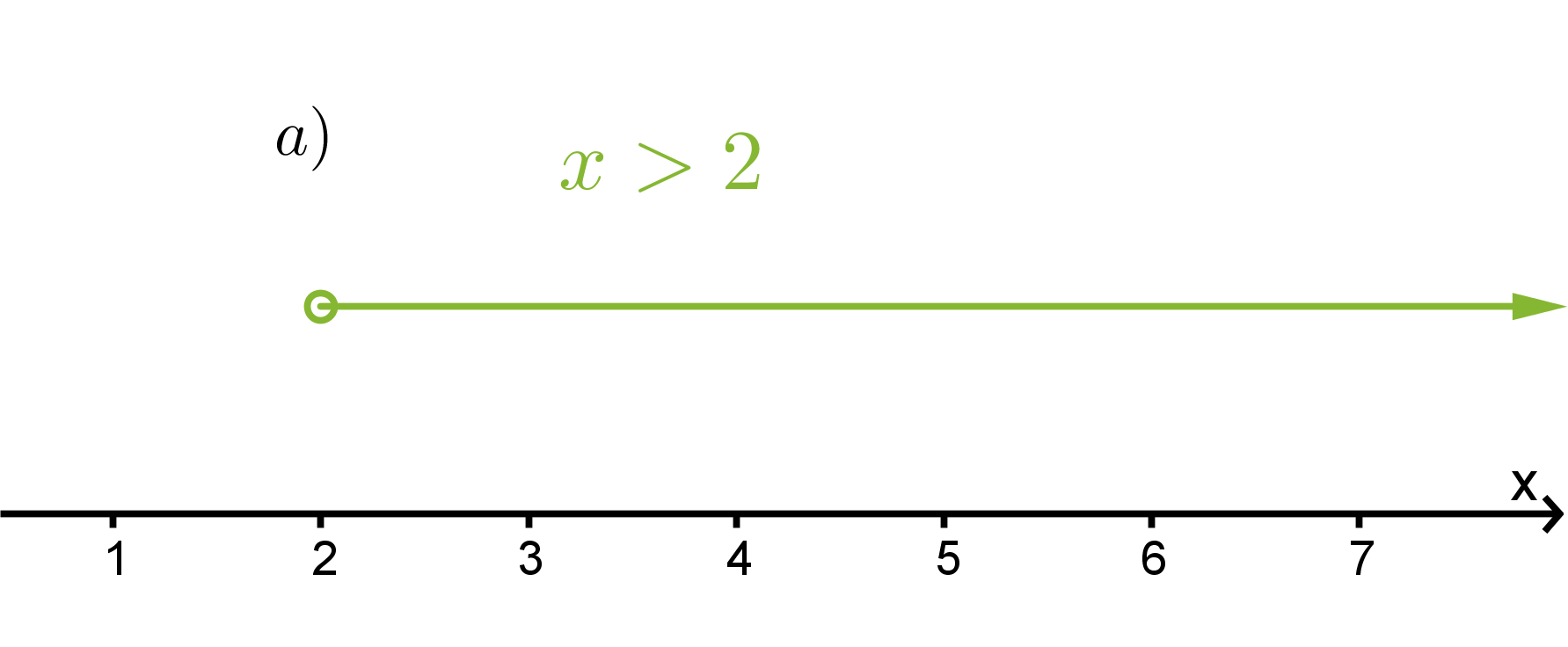
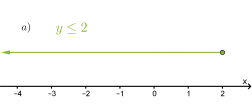
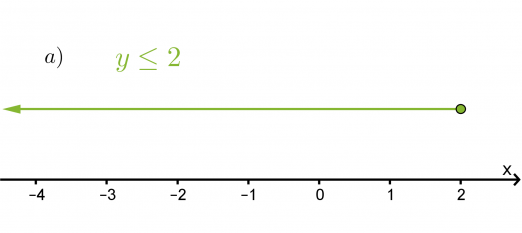
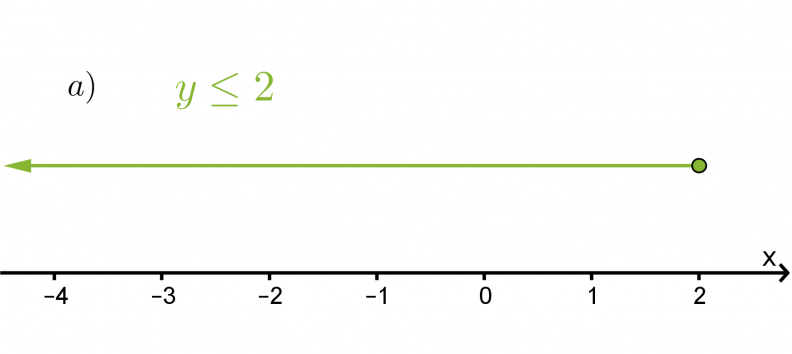
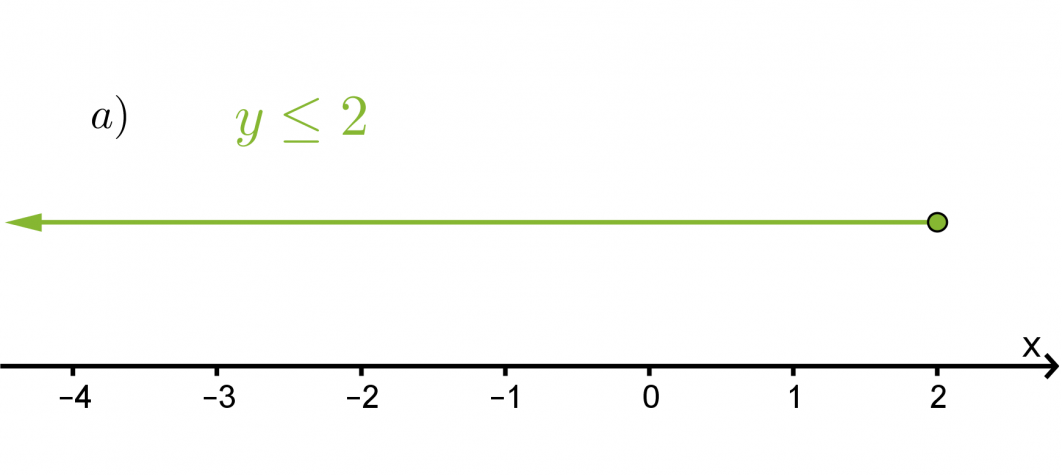
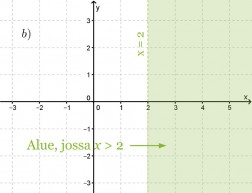
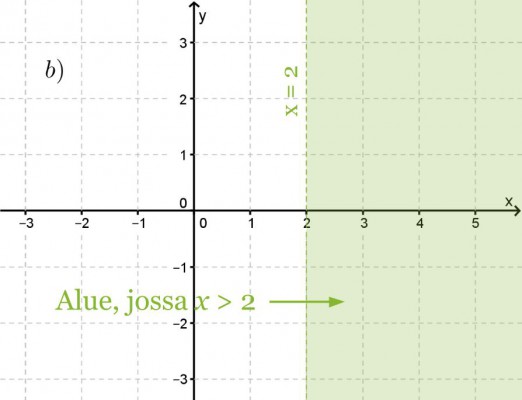
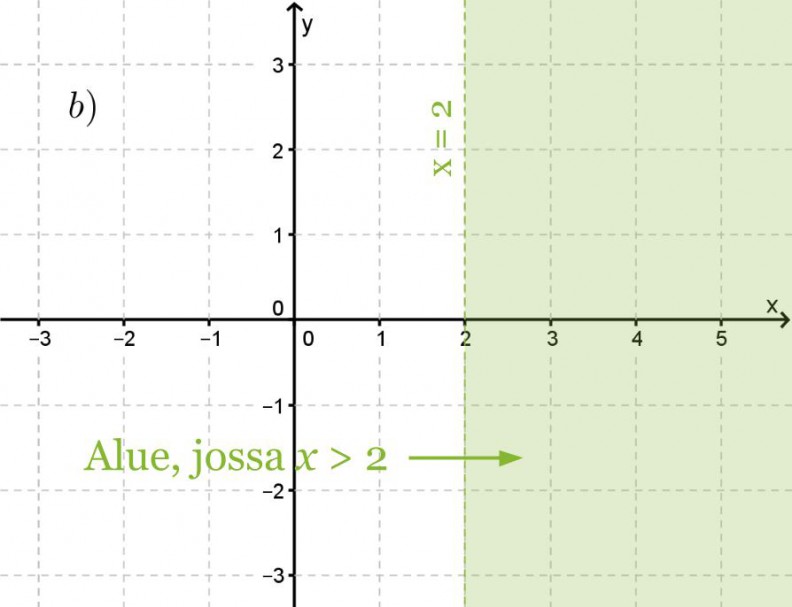
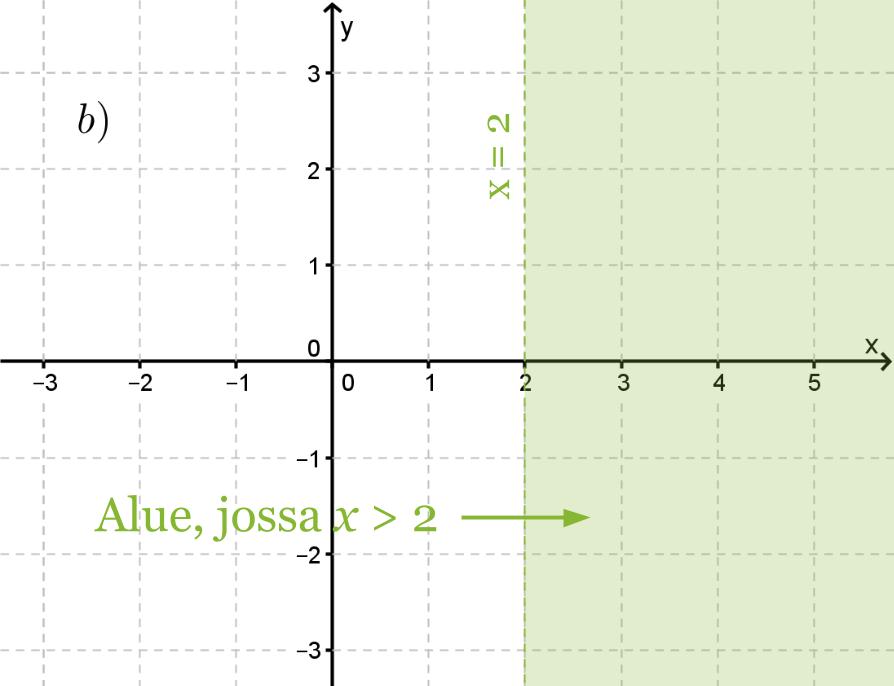
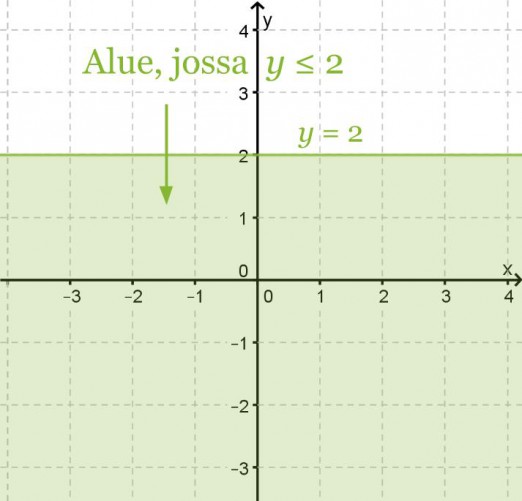
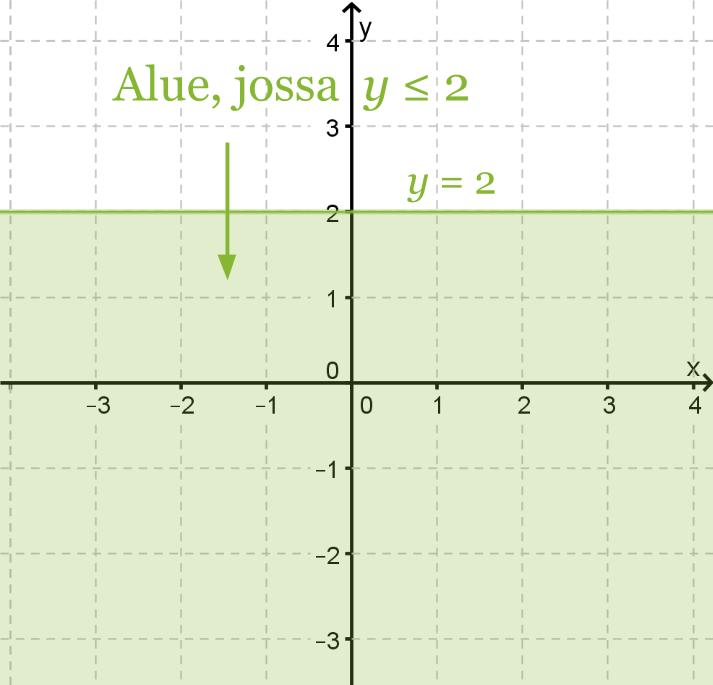
Havainnollista epäyhtälöitä x > 2 ja y ≤ 2
a) lukusuoralla
b) koordinaatistossa.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
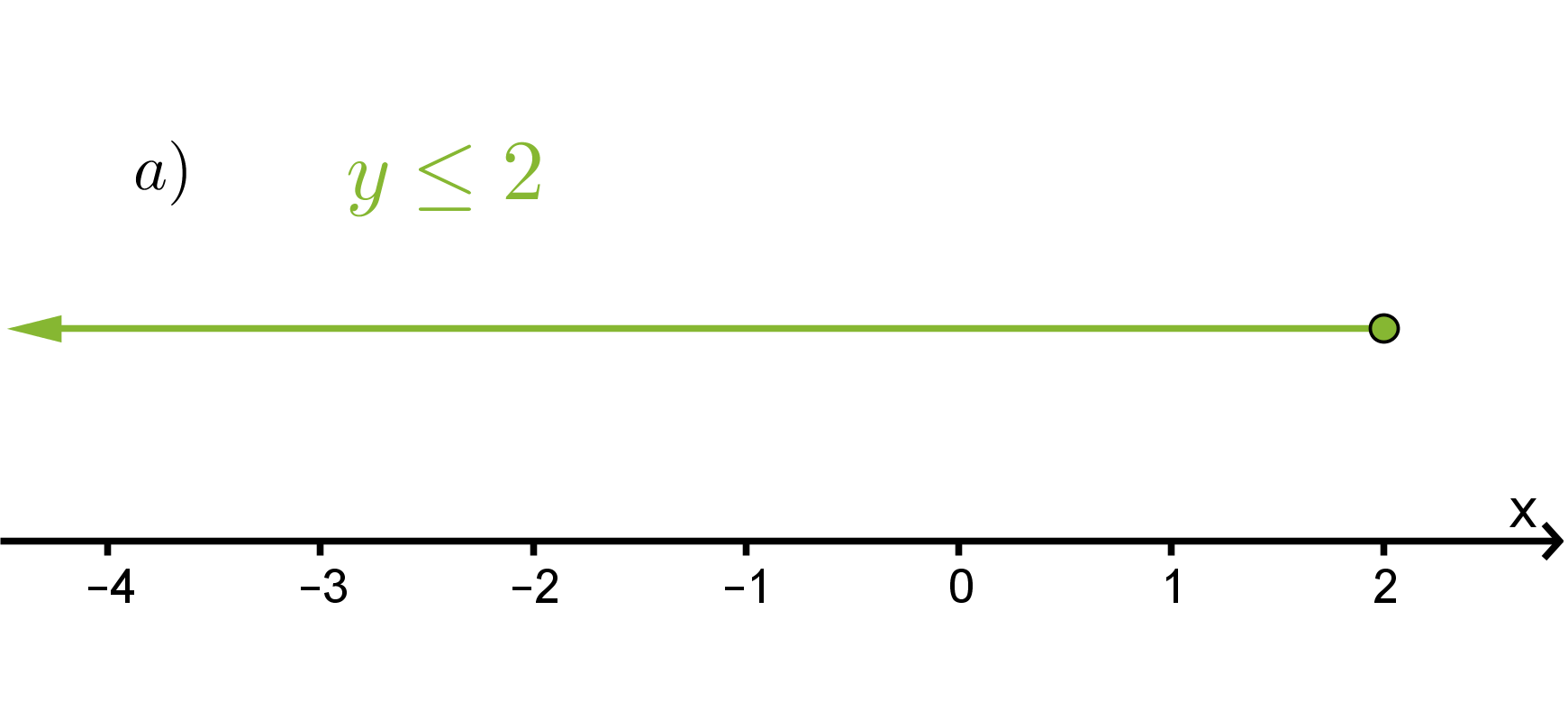
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
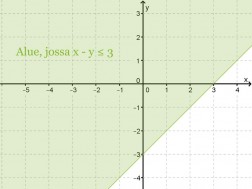
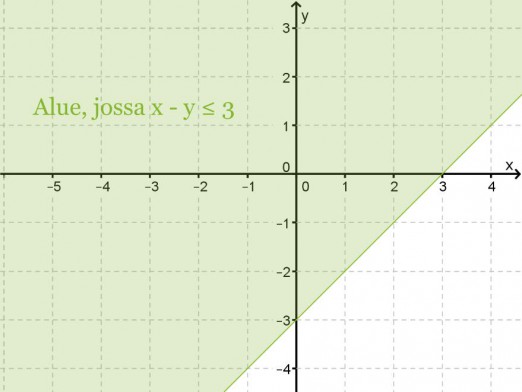
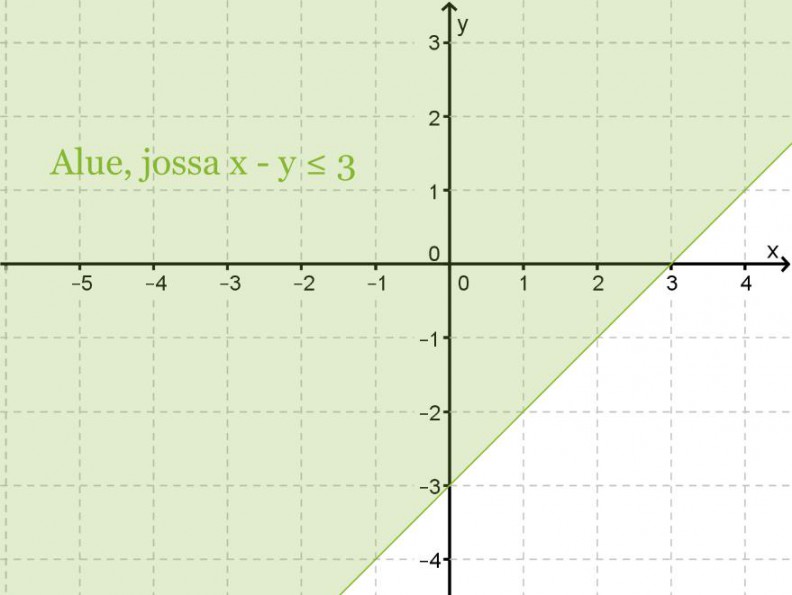
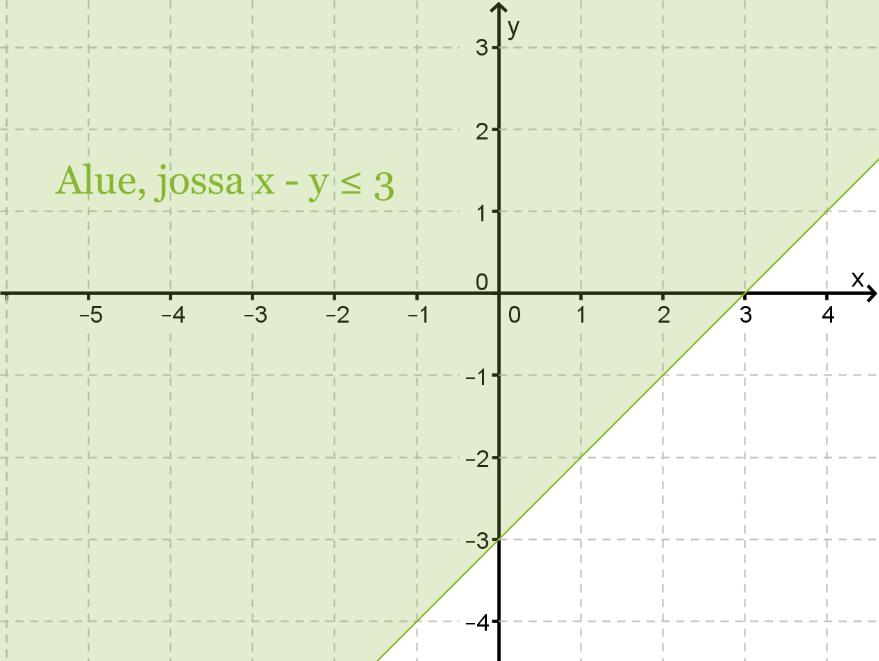
Piirrä koordinaatistoon kuva alueesta x − y ≤ 3.
Ratkaisu:
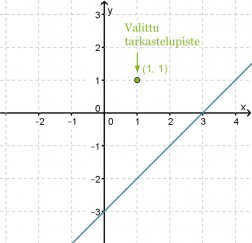
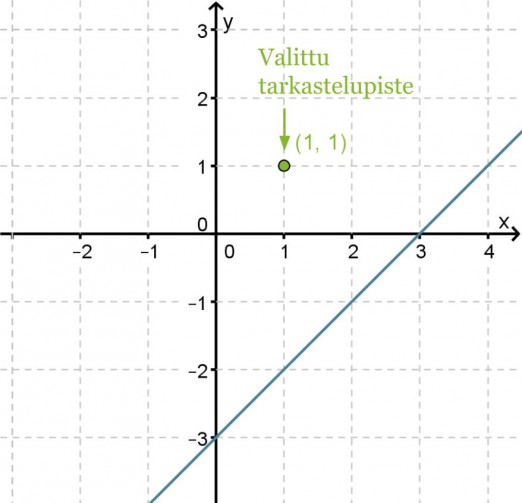
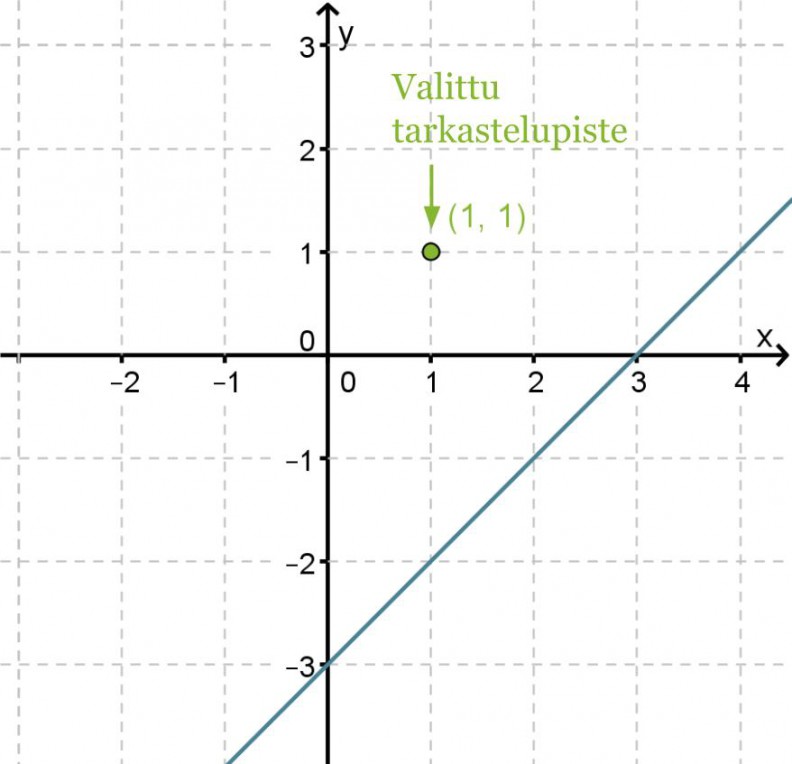
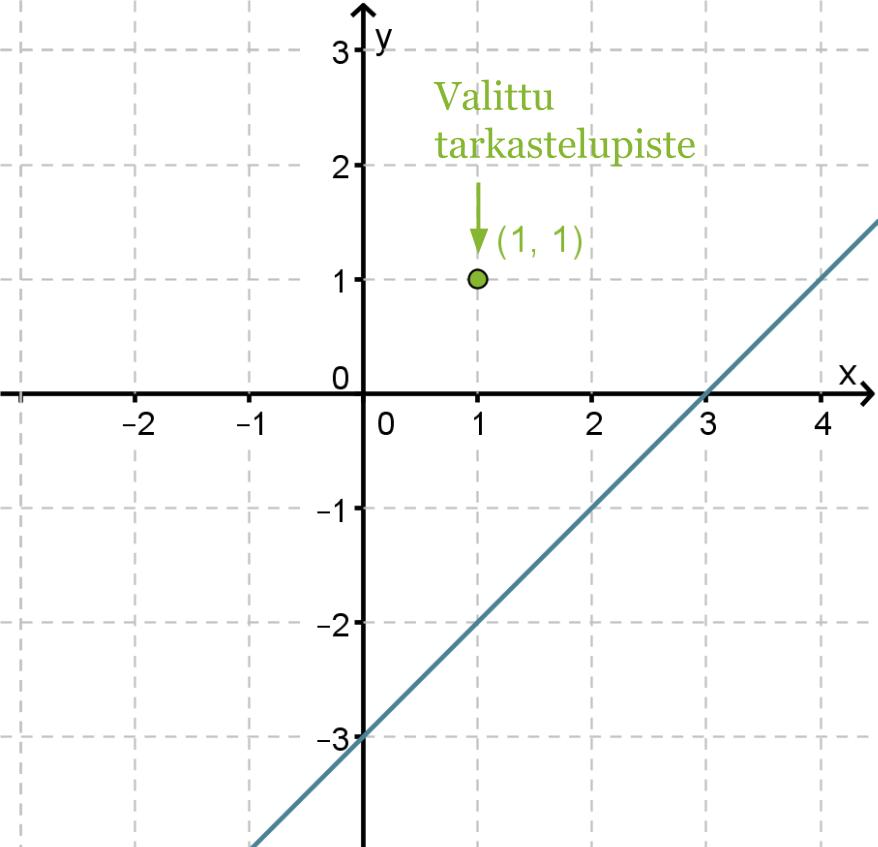
Aloitetaan tarkastelu suorasta x − y = 3, koska tämä tulee olemaan alueen rajana. Kirjoitetaan yhtälö tutumpaan muotoon, jossa yhtäsuuruusmerkin vasemmalla puolella on muuttuja y ja muut termit oikealla puolella eli y = x − 3. Piirretään suora koordinaatistoon.
Ongelmana on, että kumpi suoran puolista toteuttaa epäyhtälön. Tämän selvittämiseksi valitaan jommaltakummalta suoran puolelta tarkastelupiste ja katsotaan toteuttaako tämä piste epäyhtälön.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tarkastelupisteeksi valitaan (1, 1) ja sijoittamalla kyseinen piste epäyhtälöön x – y ≤ 3 saadaan
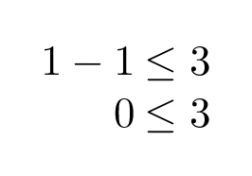
Klikkaa kuva suuremmaksi!
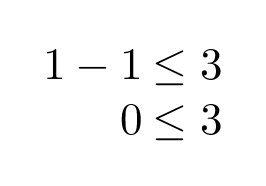
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
On totta, että nolla on pienempi kuin kolme, jolloin testipiste (1, 1) kuuluu alueeseen x – y ≤ 3.
Suoran y = x – 3 yläpuoli siis toteuttaa yhtälön x – y ≤ 3 ja varjostetaan tämä alue koordinaatistosta.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ensimmäisen asteen epäyhtälö
Epäyhtälössä yhtäsuuruusmerkin tilalla on jokin merkeistä <, >, ≤, ≥, ≠. Ensimmäisen asteen epäyhtälö ratkaistaan samoin kuin ensimmäisen asteen yhtälö, paitsi kerrottaessa tai jaettaessa negatiivisella luvulla epäyhtälömerkin suunta vaihtuu.