15. Epäyhtälöpari*
Myös epäyhtälöitä voidaan tarkastella pareittain. Epäyhtälöparissa on syytä kiinnittää huomiota siihen onko molempien epäyhtälöiden oltava voimassa samanaikaisesti, vai riittääkö että edes toinen epäyhtälöistä toteutuu.
Esimerkki 1.
Mitkä x:n arvot toteuttavat epäyhtälöparit?
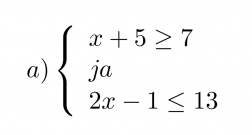
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
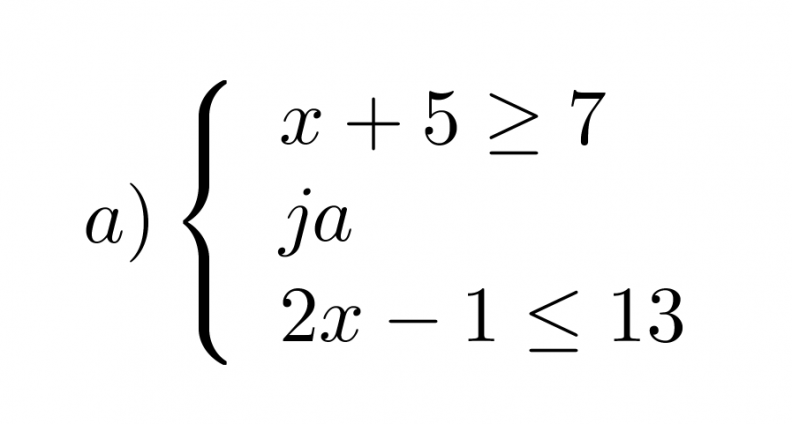
Klikkaa kuva suuremmaksi!
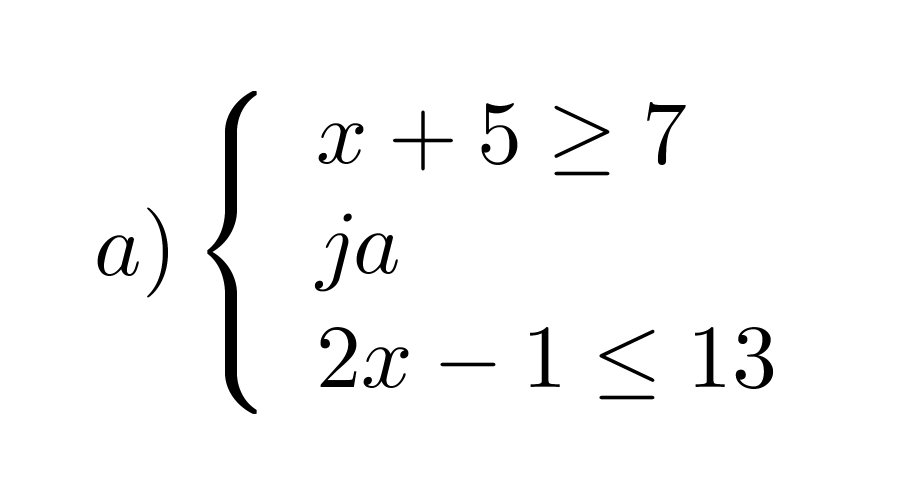
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Ratkaistaan molemmat epäyhtälöt aluksi normaalisti erikseen.
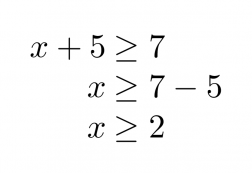
Klikkaa kuva suuremmaksi!
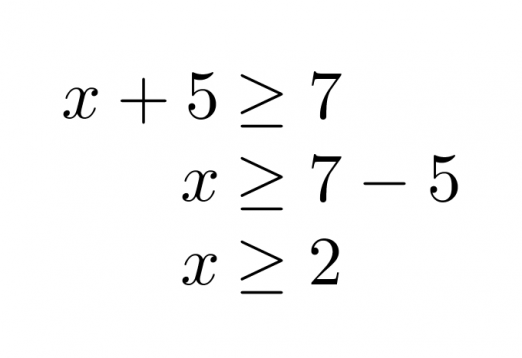
Klikkaa kuva suuremmaksi!
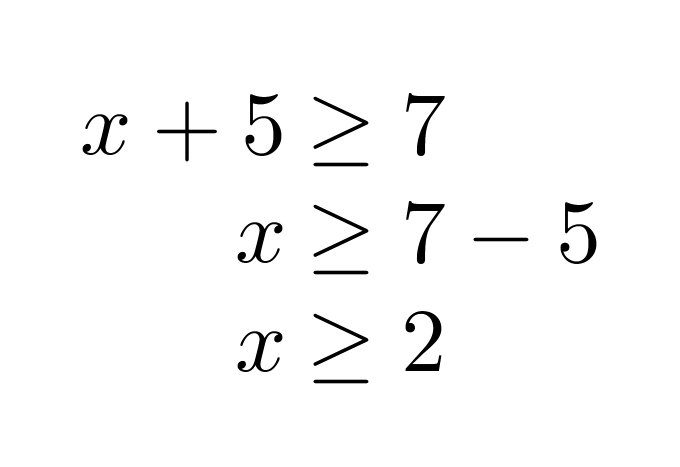
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
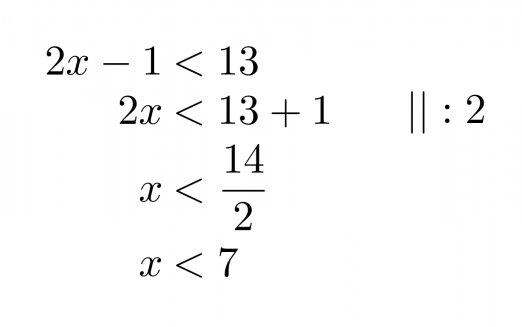
Klikkaa kuva suuremmaksi!
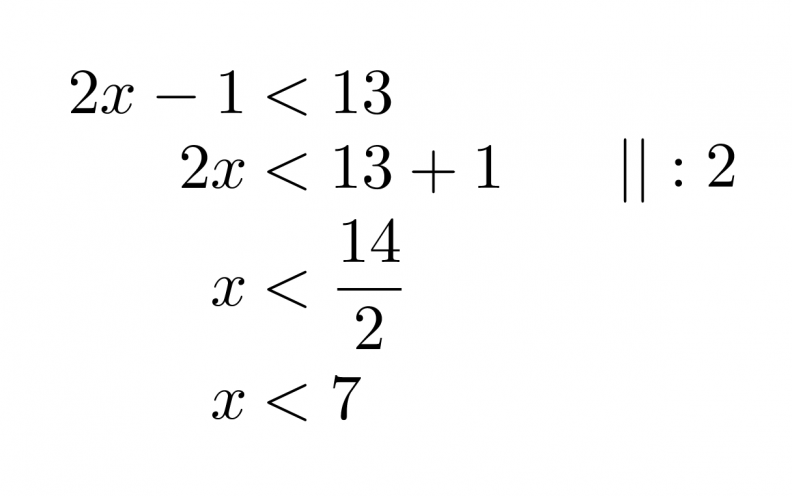
Klikkaa kuva suuremmaksi!
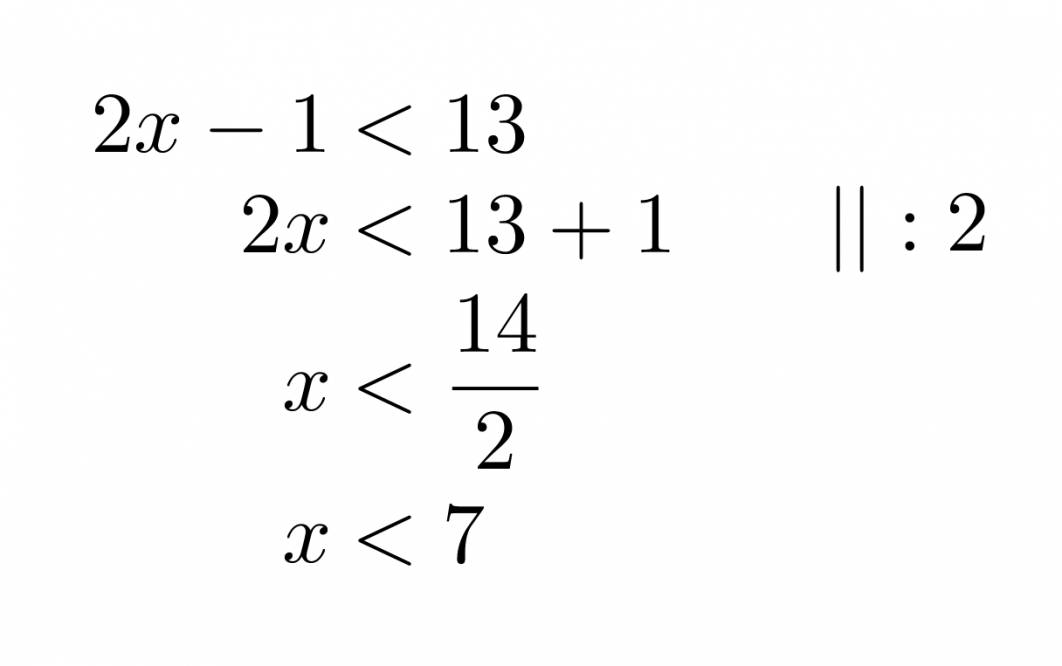
Klikkaa kuva suuremmaksi!
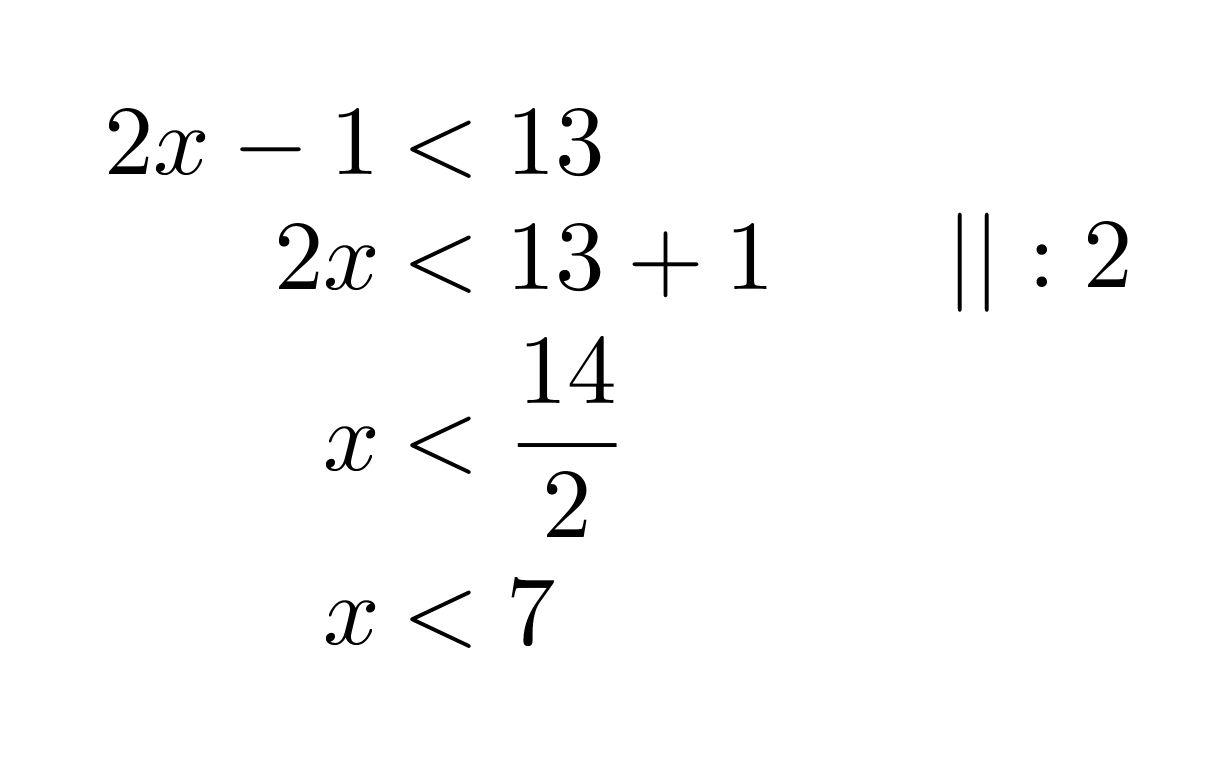
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
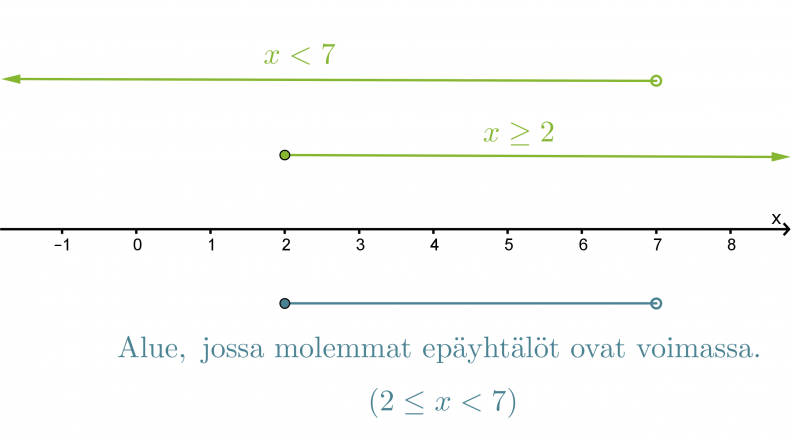
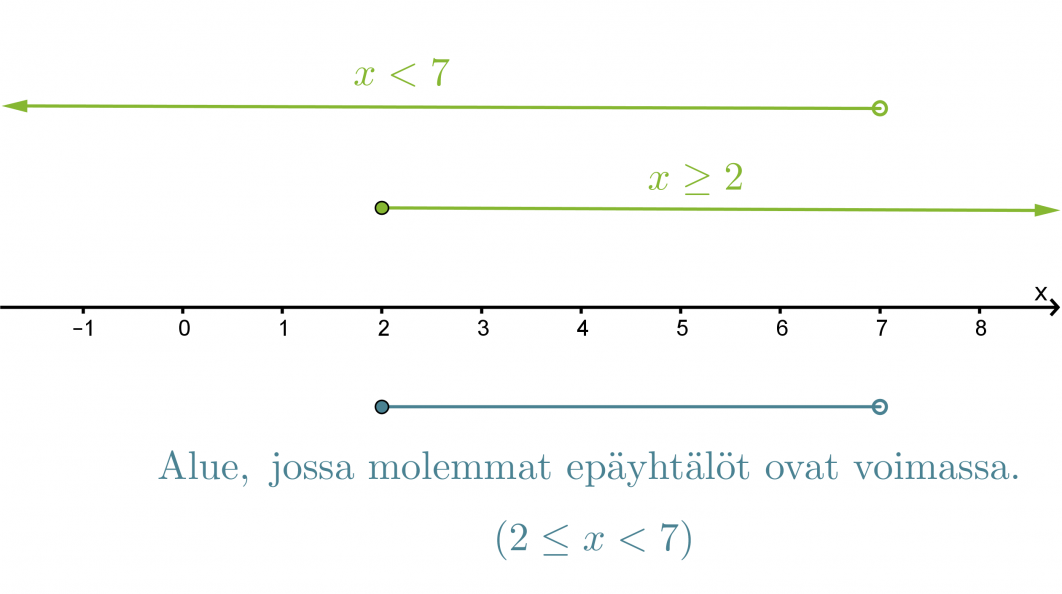
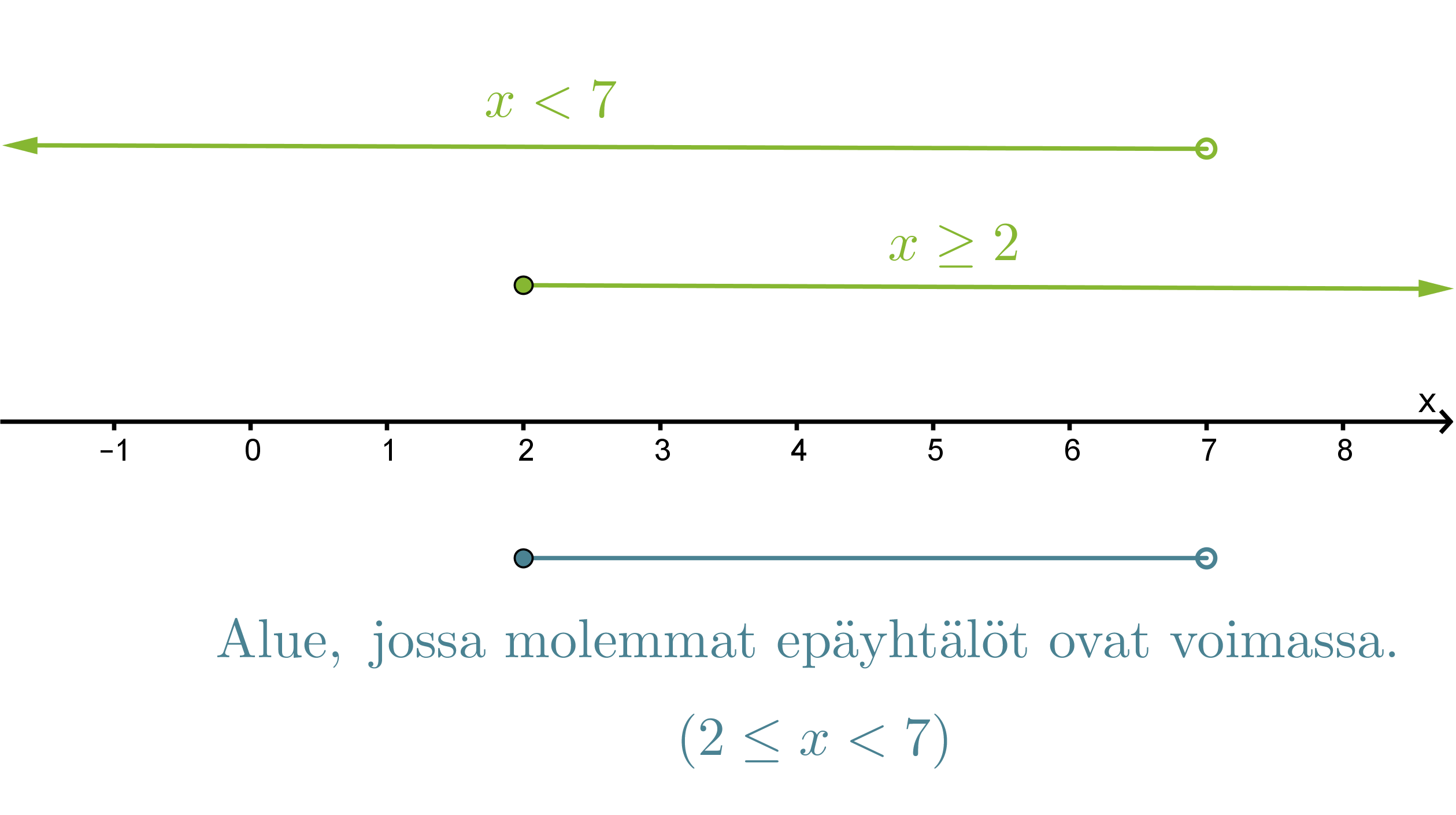
Etsitään lukusuoran avulla alue, jossa molemmat epäyhtälöt toteutuvat.
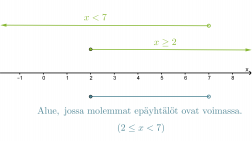
Klikkaa kuva suuremmaksi!
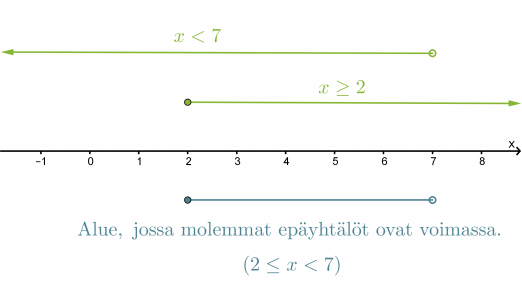
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: 2 ≤ x < 7
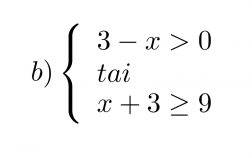
Klikkaa kuva suuremmaksi!
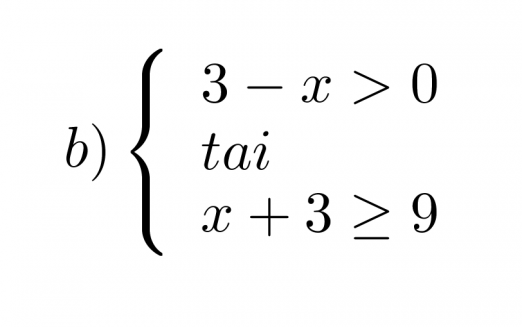
Klikkaa kuva suuremmaksi!
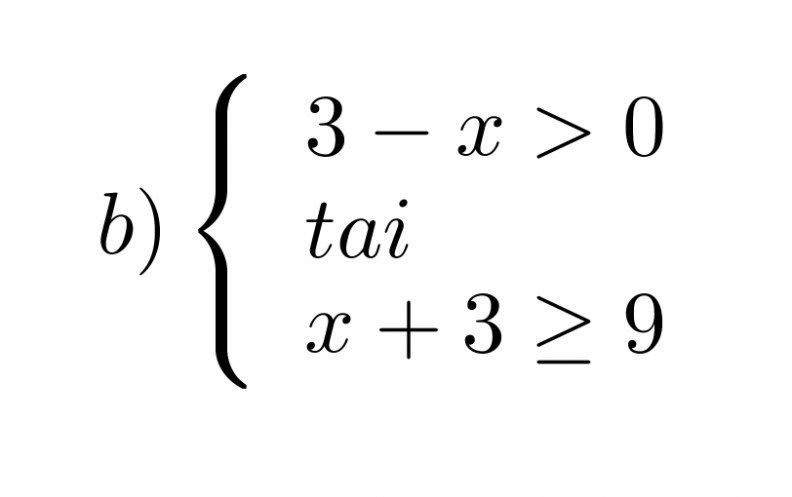
Klikkaa kuva suuremmaksi!
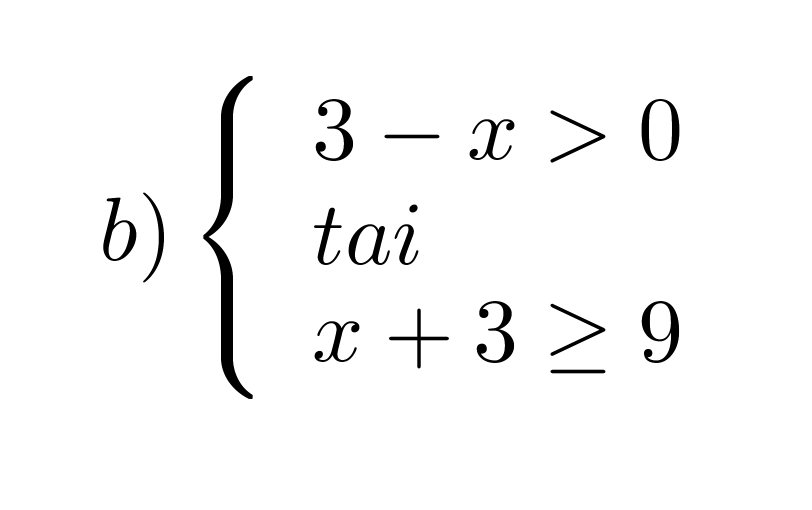
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
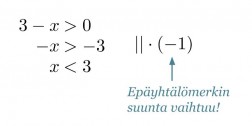
Ratkaistaan molemmat epäyhtälöt aluksi normaalisti erikseen.
Klikkaa kuva suuremmaksi!
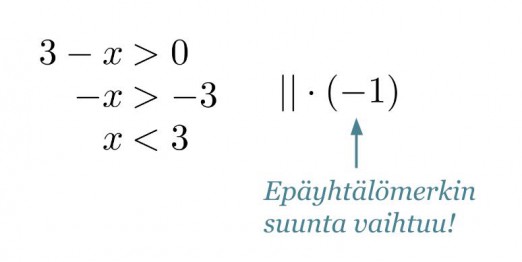
Klikkaa kuva suuremmaksi!
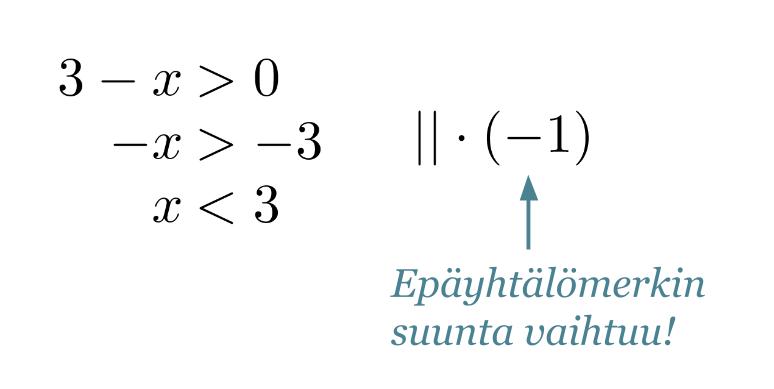
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
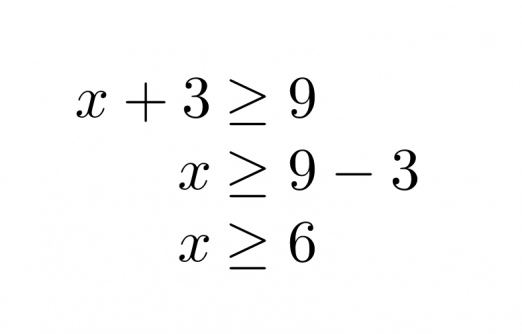
Klikkaa kuva suuremmaksi!
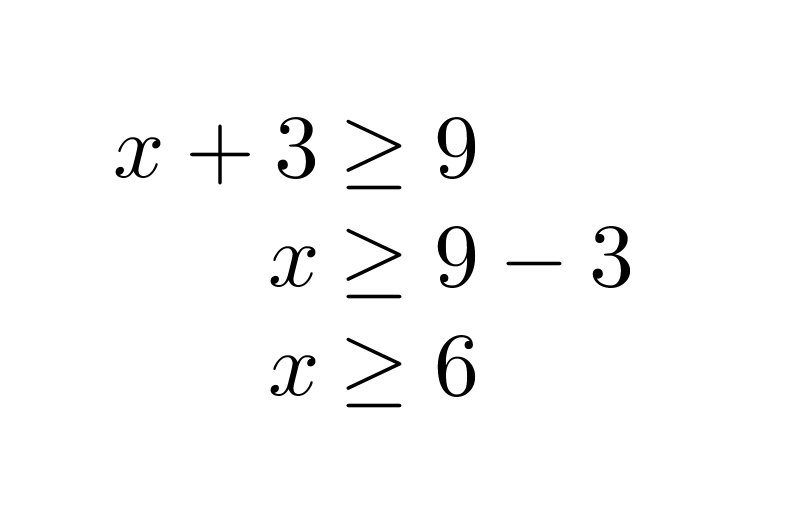
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
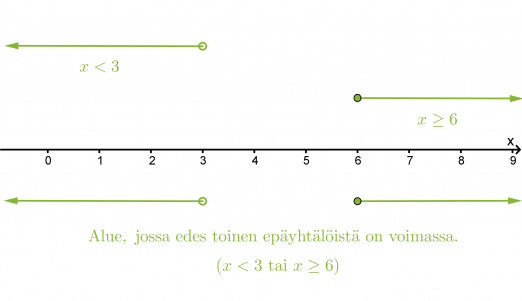
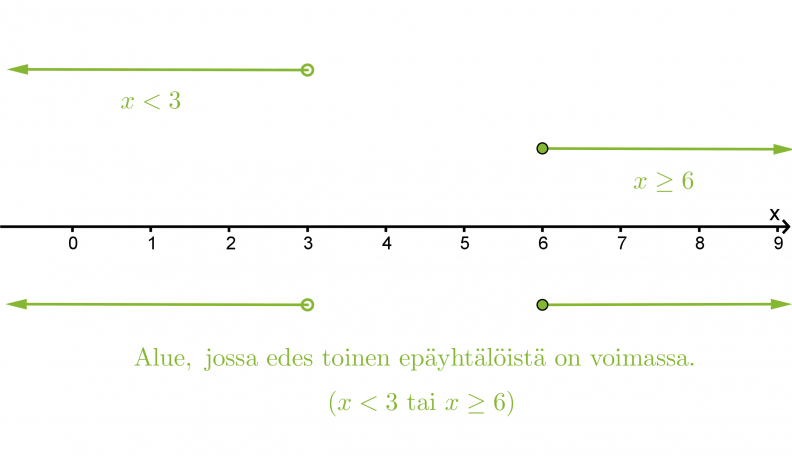
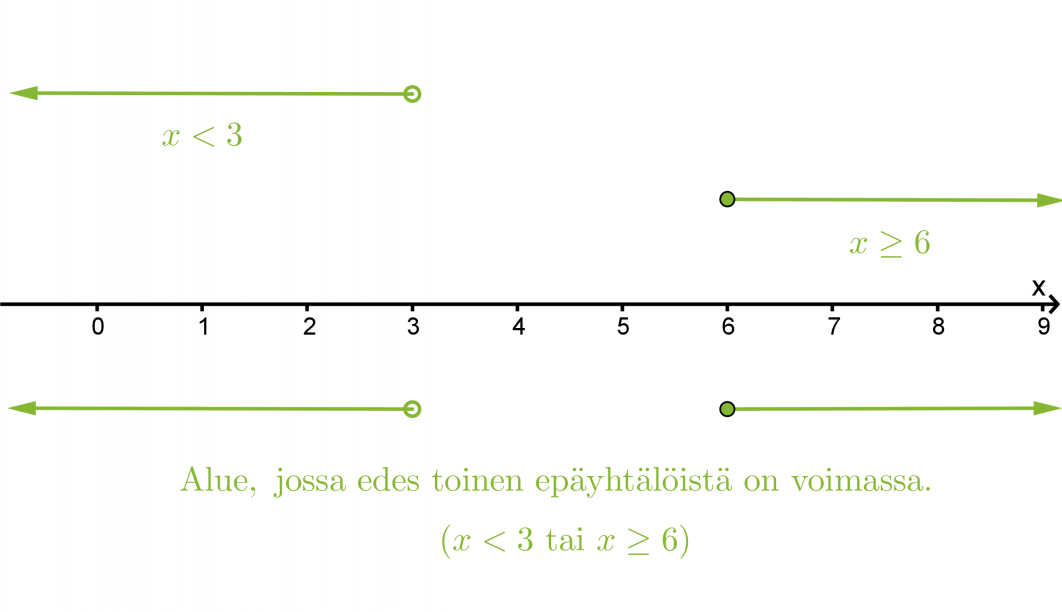
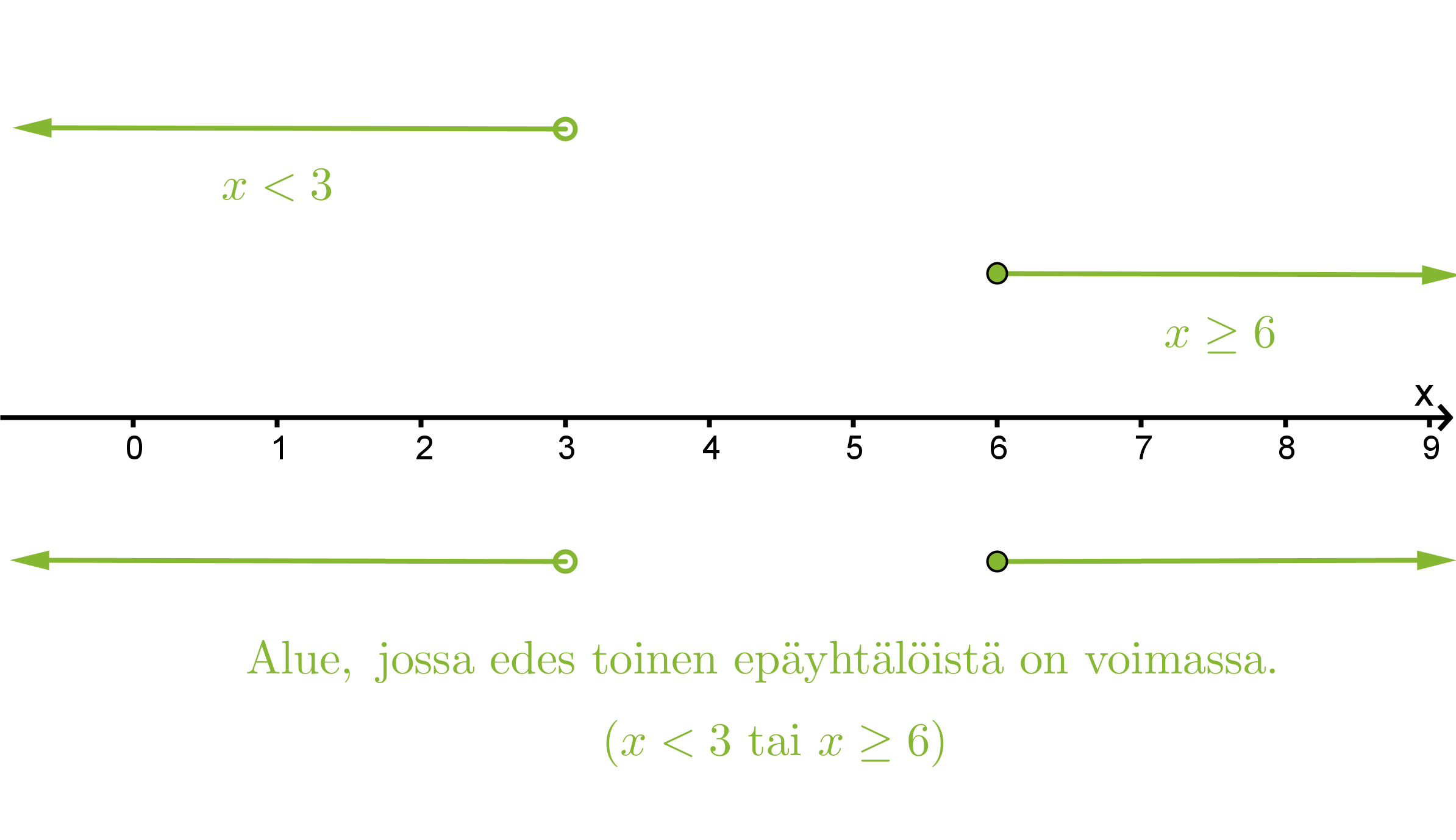
Etsitään lukusuoran avulla alue, jossa edes toinen epäyhtälöistä toteutuu.

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: x < 3 tai x ≥ 6
Huom! Merkintätavasta 2 ≤ x < 7 käytetään nimitystä kaksoisepäyhtälö, koska siinä on samanaikaisesti kaksi erisuuruusmerkkiä. Jos kahden epäyhtälön on toteuduttava samanaikaisesti, kirjoitetaan epäyhtälöpari yleensä kaksoisepäyhtälönä.
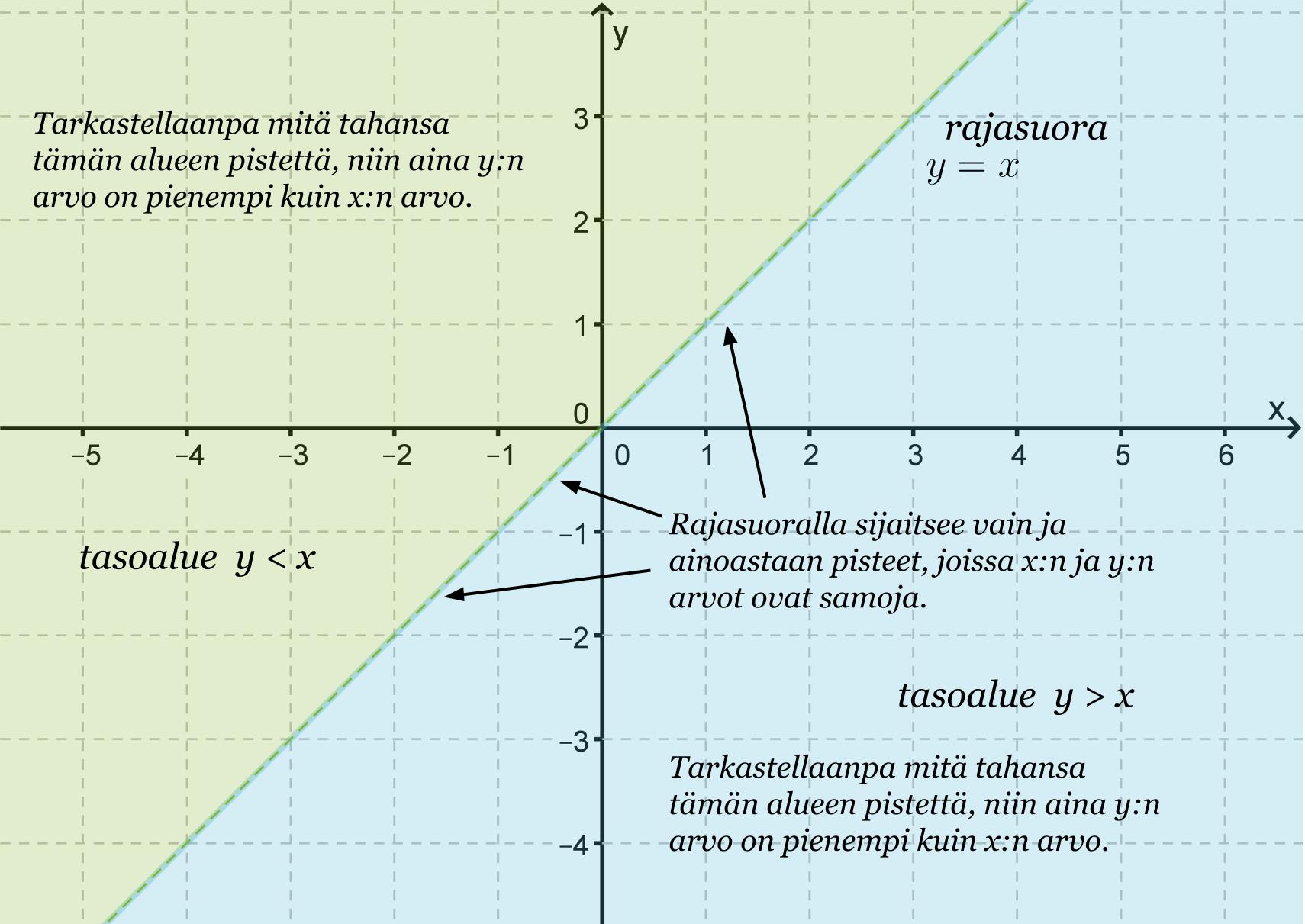
Epäyhtälöitä, joissa on vaan yksi muuttuja, on helpointa havainnollistaa lukusuoralla. Koordinaatistossa sitä vastoin voidaan tarkastella myös kahden muuttuja epäyhtälöitä. Tutkitaan minkälaisiin alueisiin suora y = x jakaa xy-koordinaatiston.
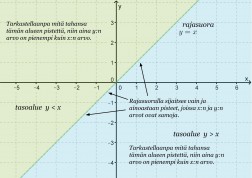
Klikkaa kuva suuremmaksi!
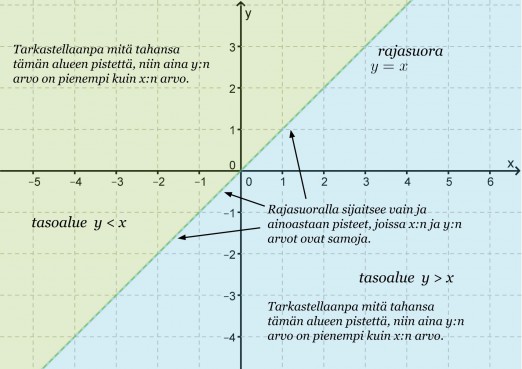
Klikkaa kuva suuremmaksi!
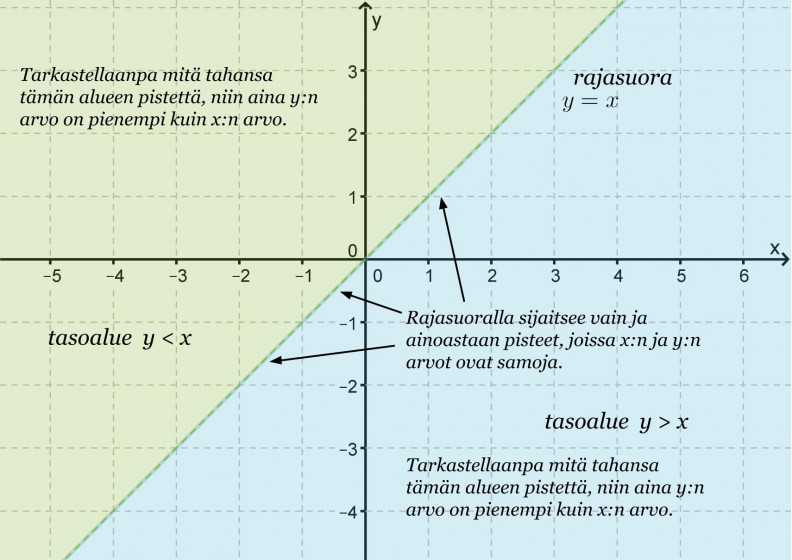
Klikkaa kuva suuremmaksi!
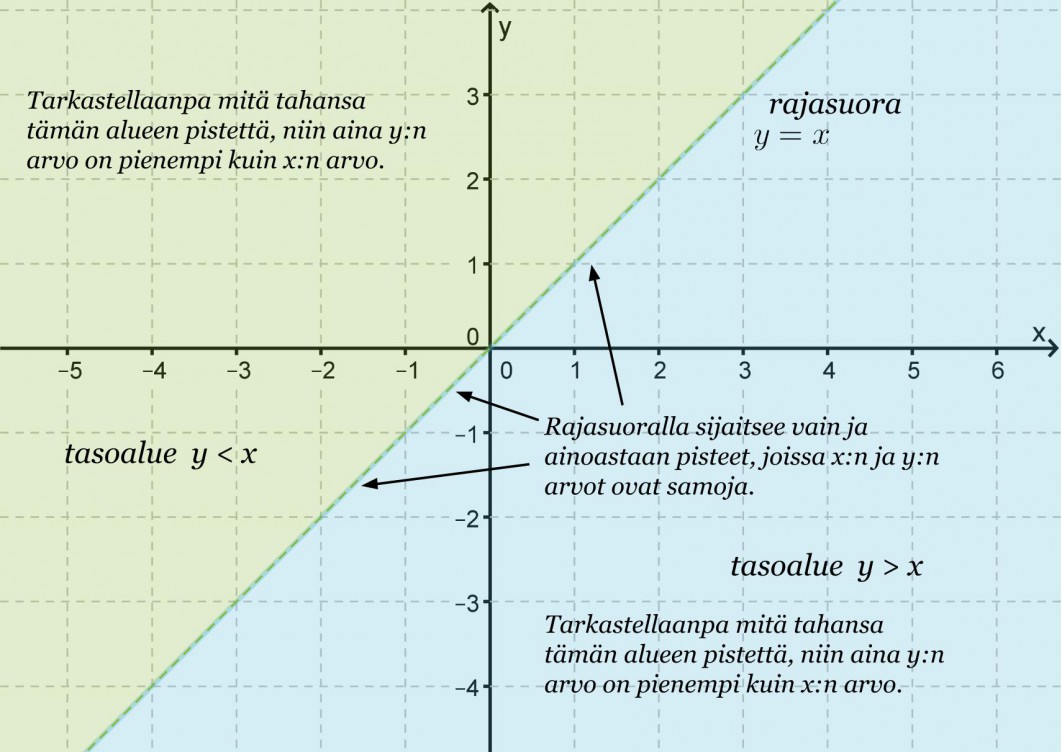
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Useamman kuin yhden rajasuoran muodostamat tasoalueet löytyvät helpoiten kokeilemalla. Tällöin valitaan jokaisesta muodostuneesta tasoalueesta tarkastelupiste ja tutkitaan mikä pisteistä toteuttaa molemmat epäyhtälöt.
Ainoastaan yhdessä tasoalueessa kaikki epäyhtälöt ovat tosia.
Esimerkki 2.
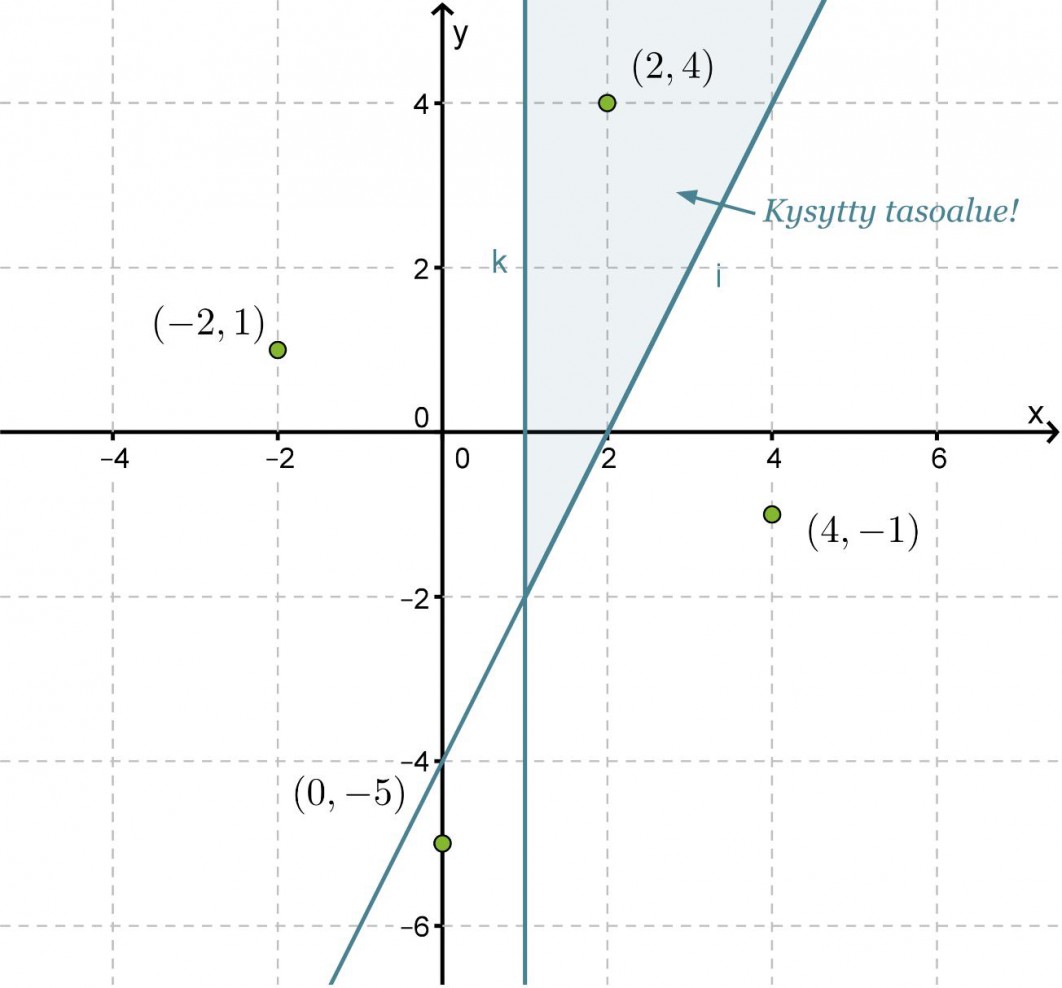
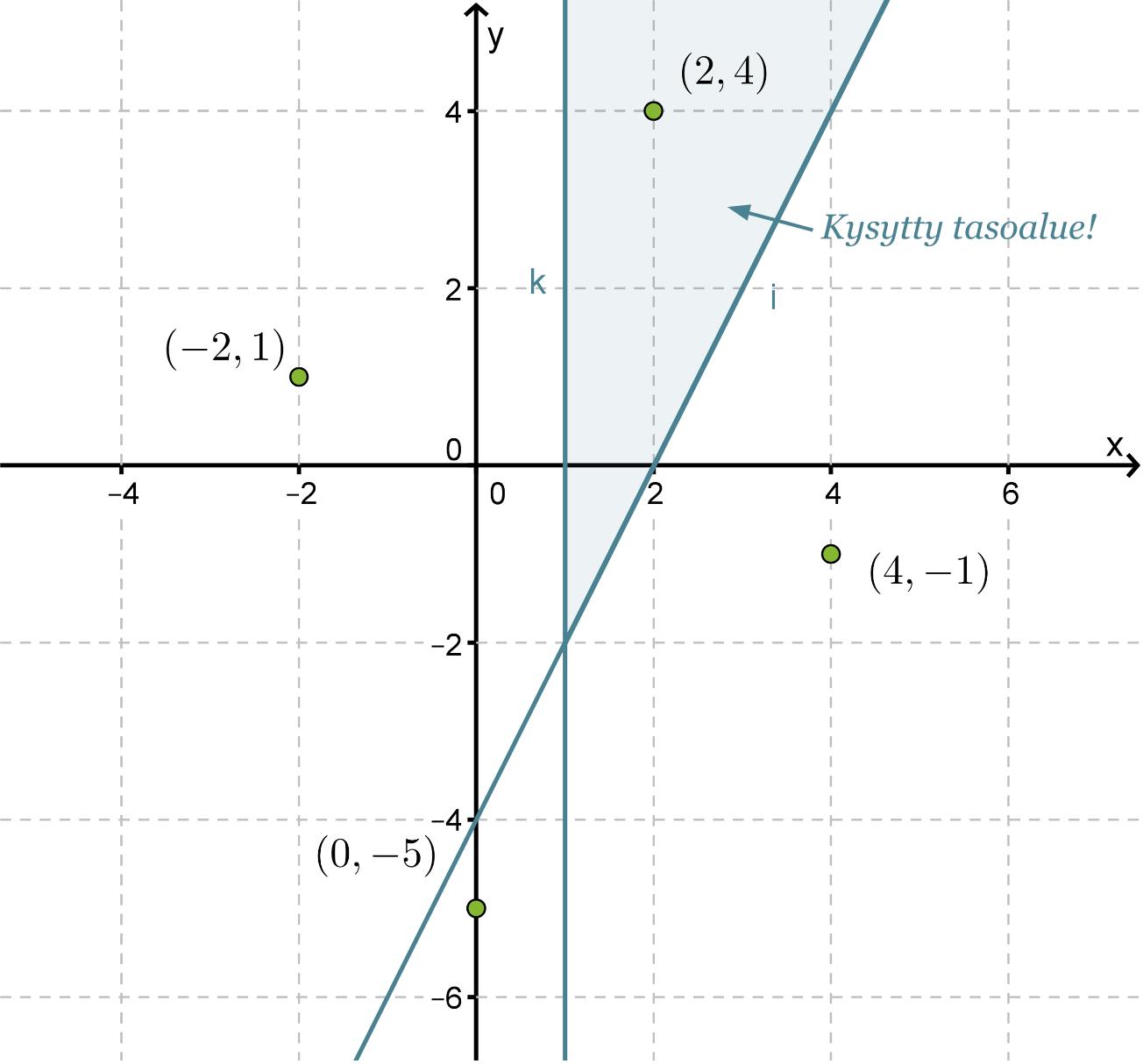
Missä tasoalueessa sijaitsevat pisteet, jotka toteuttavat epäyhtälöt y > 2x − 4 ja x ≥ 1?
Ratkaisu:
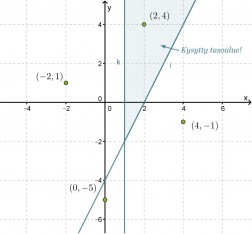
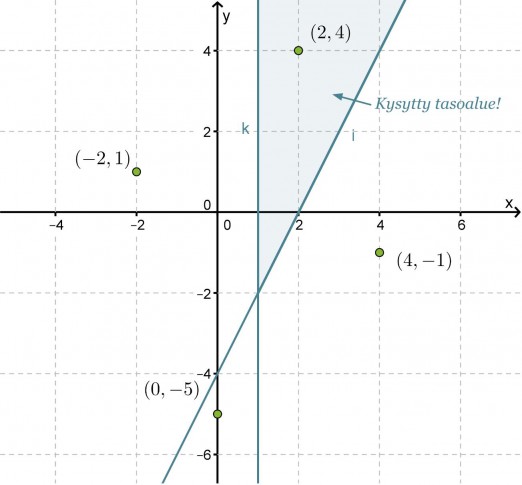
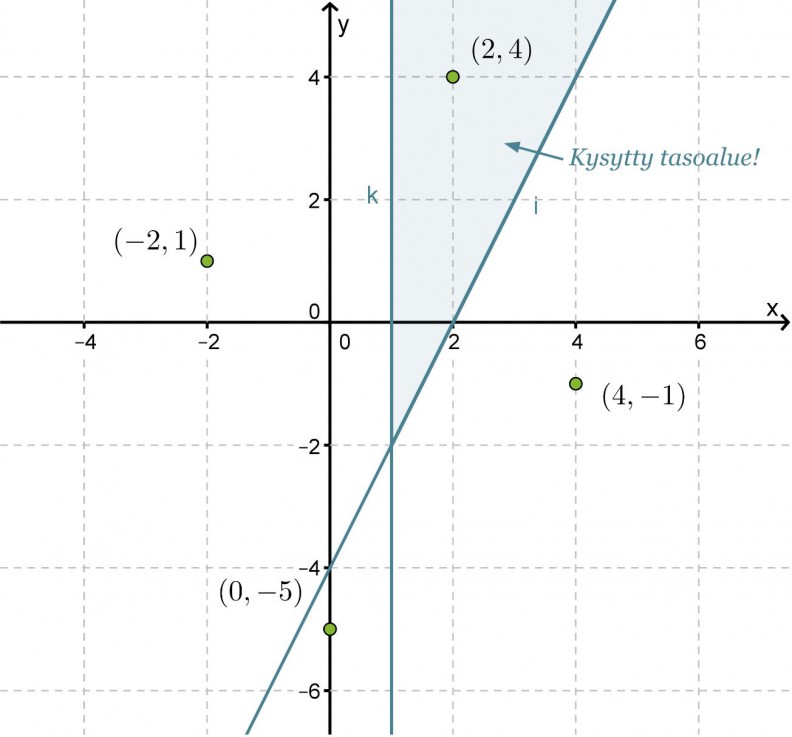
Koordinaatiston rajasuorina ovat ja y = 2x − 4 ja x = 1, jotka jakavat xy-tason neljään tasoalueeseen. Rajasuora y = 2x − 4 piirretään katkoviivoin, koska sen pisteet eivät enää toteuta vaadittua epäyhtälöä. Valitaan jokaisesta tason osasta tarkastelupisteet, sijoitetaan ne molempiin epäyhtälöihin ja tutkitaan mikä niistä toteuttaa molemmat epäyhtälöt.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
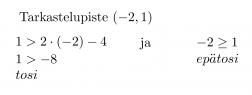
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
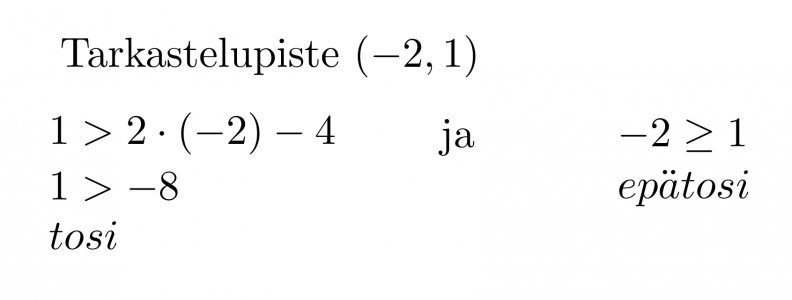
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tarkastelupiste (2, 4) toteuttaa molemmat epäyhtälöt, jolloin kysytty tasoalue on se, jossa tämä piste sijaitsee.
Huom! Epäyhtälöiden toteutumistarkastelut oltaisiin voitu lopettaa pisteen (2, 4) jälkeen, koska tasoalueita, jotka toteuttavat molemmat epäyhtälöt samanaikaisesti voi olla ainoastaan yksi. Mahdollisen virheen havaitsemiseksi on kuitenkin hyvä tutkia kaikki tarkastelupisteet.
Avoin matematiikka 9Osio 1: Lausekkeita ja funktioita5.6.2014
Epäyhtälöpari
Epäyhtälöparit ratkaistaan siten, että ensiksi molemmat epäyhtälöt ratkaistaan erikseen. Epäyhtälöparissa esiintyvä boolen operaattori määrää miten ratkaisut pitää yhdistää.
Jos epäyhtälöparissa esiintyy sana