1. Desimaaliluvut
Kun murtoluku muutetaan desimaaliluvuksi, saadaan joko päättyvä desimaaluku tai päättymätön jaksollinen desimaaliluku, jossa sama desimaalien sarja toistuu loputtomiin. Päättymättömät jaksolliset desimaaliluvut esitetään siten, että desimaaliluvun jakso kirjoitetaan näkyviin vähintään kaksi kertaa ja luvun loppuun laitetaan kolme pistettä. Vaihtoehtoisesti jakso voidaan kirjoittaa vain kerran ja laittaa sen päälle viiva.
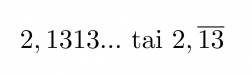
Klikkaa kuva suuremmaksi!
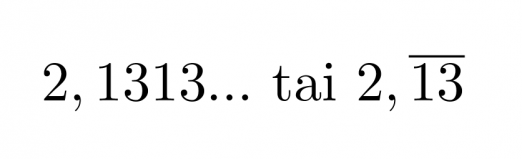
Klikkaa kuva suuremmaksi!
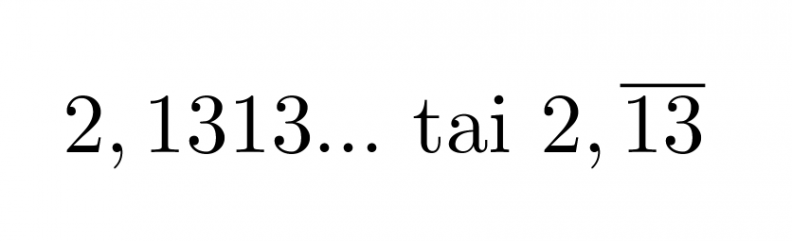
Klikkaa kuva suuremmaksi!
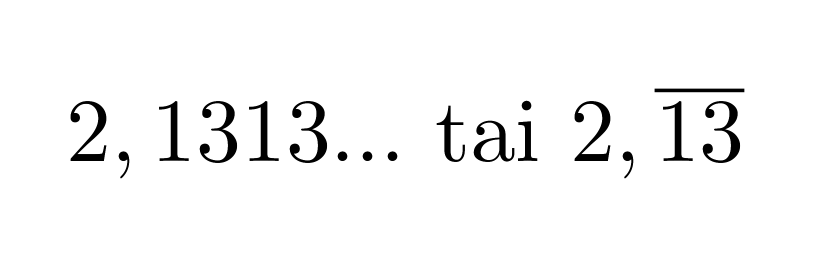
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Jokainen päättyvä desimaaliluku tai päättymätön jaksollinen desimaaliluku voidaan muuntaa murtoluvuksi. Sen sijaan jaksottomat päättymättömät desimaaliluvut ovat irrationaalilukuja, joita ei voi kirjoittaa murtolukumuodossa.
Kun desimaaliluvuilla suoritetaan laskutoimituksia, on vastausten tarkkuuteen kiinnitettävä erityistä huomiota. Luvun merkitseviksi numeroiksi katsotaan kaikki muut paitsi desimaaliluvun alussa ja kokonaisluvun lopussa olevat nollat. Joissakin tapauksissa kokonaisluvun lopussakin olevat nollat voivat olla merkitseviä, mikä ilmenee asiayhteydestä.
Kerto- ja jakolasku
- Vastausksessa saa olla korkeintaan yhtä monta merkitsevää numeroa kuin niitä on epätarkimmassa lähtöarvossa
- Jos vastaus vaaditaan tietyllä tarkkuudella, on lähtöarvot varmuuden vuoksi otettava vähintään yhtä merkitsevää numeroa tarkemmin
Esimerkki 1.
Esitetään desimaaliluvut yläviivan avulla.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Muutetaan desimaaliluvut murtoluvuiksi.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 3.
Muunnetaan luku x = 1,123123… murtoluvuksi.
Koska desimaalien sarja toistuu loputtomiin, ei desimaaleja voida tarkastella sellaisenaan. Desimaaliluvun jaksossa on kolme lukua 123. Jos desimaaliluku kerrotaan 1000:lla, on uuden luvun desimaaliosa samanlainen kuin alkuperäisen luvun desimaaliosa.
1000x = 1123,123123…
Kun vähennetään luvut 1000x ja x toisistaan, päästään lukujen desimaaliosista kokonaan eroon.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Vastaus: Luku 1,123123… on murtolukuna
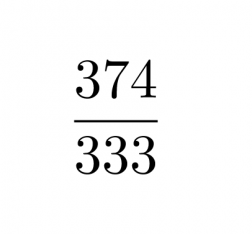
Klikkaa kuva suuremmaksi!
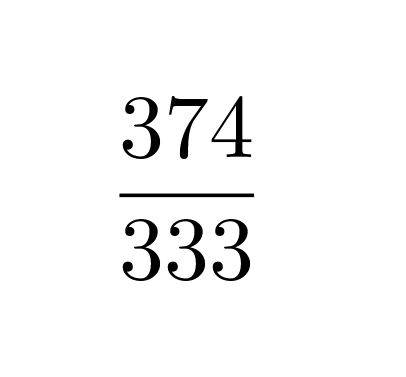
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 4.
Tutkitaan eri lukujen merkitsevien numeroiden lukumäärää.
- Kokonaisluvussa 40 000 on yksi merkitsevä numero.
- Desimaaliluvussa 0,140 on kolme merkitsevää numeroa.
- Desimaaliluvussa 0,02 on yksi merkitsevä numero.
- Desimaaliluvussa 79,10 on neljä merkitsevää numeroa.
- Kokonaisluvussa 7001 on neljä merkitsevää numeroa.
- Kokonaisluvussa 310 on kaksi tai kolme merkitsevää numeroa riippuen siitä, onko luku pyöristetty.
Yhteen- ja vähennyslasku