2. Tekijöihin jako
Tekijä on yhteisnimitys kertolaskun kertojalle ja kerrottavalle. Kun luku esitetään tulona, sanotaan sen olevan jaettu tekijöihin. Tekijöihin jakoa voidaan jatkaa aina alkutekijöihin asti, jolloin luku esitetään alkulukujen tulona.
Alkuluku on luku, joka on jaollinen ainoastaan luvulla 1 ja itsellään. Alkuluvulla itsellään on siis tasan kaksi tekijää. Jos luku ei ole alkuluku, sanotaan sitä yhdistetyksi luvuksi. Jokainen kokonaisluku (≥2) voidaan esittää ainoastaan yhdellä tavalla alkulukujen tulona. Yleensä alkutekijät asetetaan suuruusjärjestykseen ja samat alkutekijät kootaan yhteen potenssiksi.
Esimerkki 1.
Jaetaan luku 140 tekijöihin ja edelleen alkutekijöihin.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Lukujen a ja b suurin yhteinen tekijä on suurin sellainen luonnollinen luku, jolla molemmat luvuista ovat jaollisia. Se saadaan jakamalla luvut alkutekijöihinsä ja muodostamalla lukujen yhteisten tekijöiden tulo.
Lukujen a ja b pienin yhteinen jaettava on pienin luonnollinen luku, joka on jaollinen sekä luvulla a että b. Se saadaan jakamalla luvut alkutekijöihinsä ja muodostamalla lukujen kaikkien tekijöiden tulo.
Esimerkki 2.
Määritetään lukujen 140 ja 180 suurin yhteinen tekijä sekä pienin yhteinen jaettava.
Jaetaan luvut ensiksi alkutekijöihinsä.
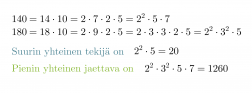
Klikkaa kuva suuremmaksi!
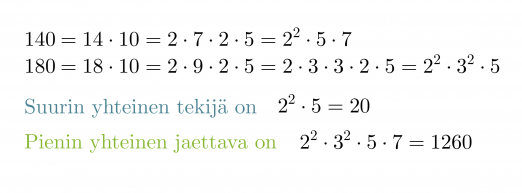
Klikkaa kuva suuremmaksi!
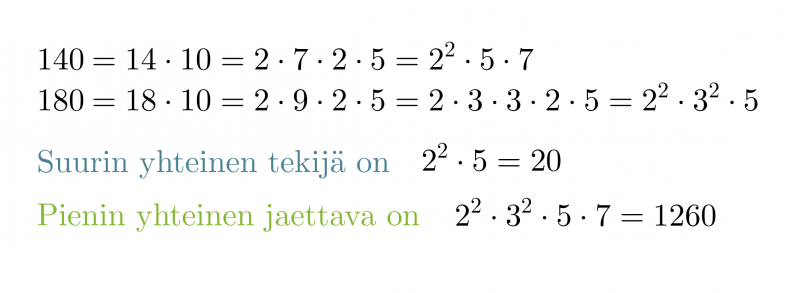
Klikkaa kuva suuremmaksi!
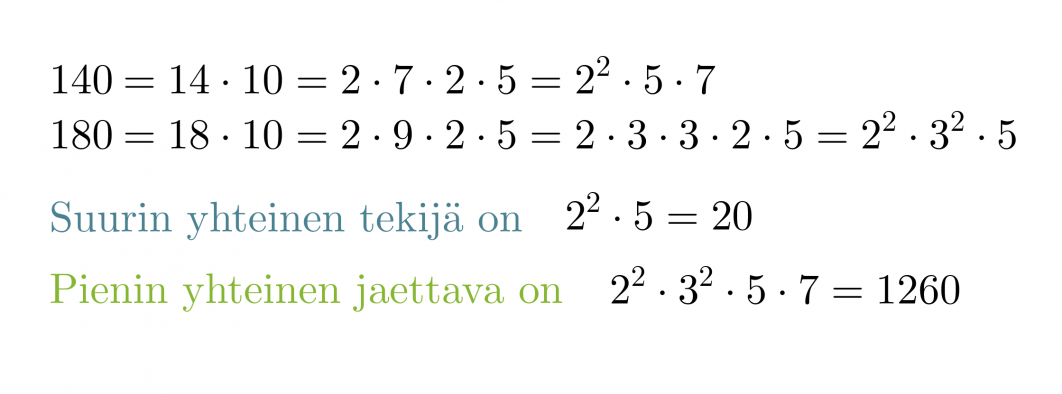
Klikkaa kuva suuremmaksi!
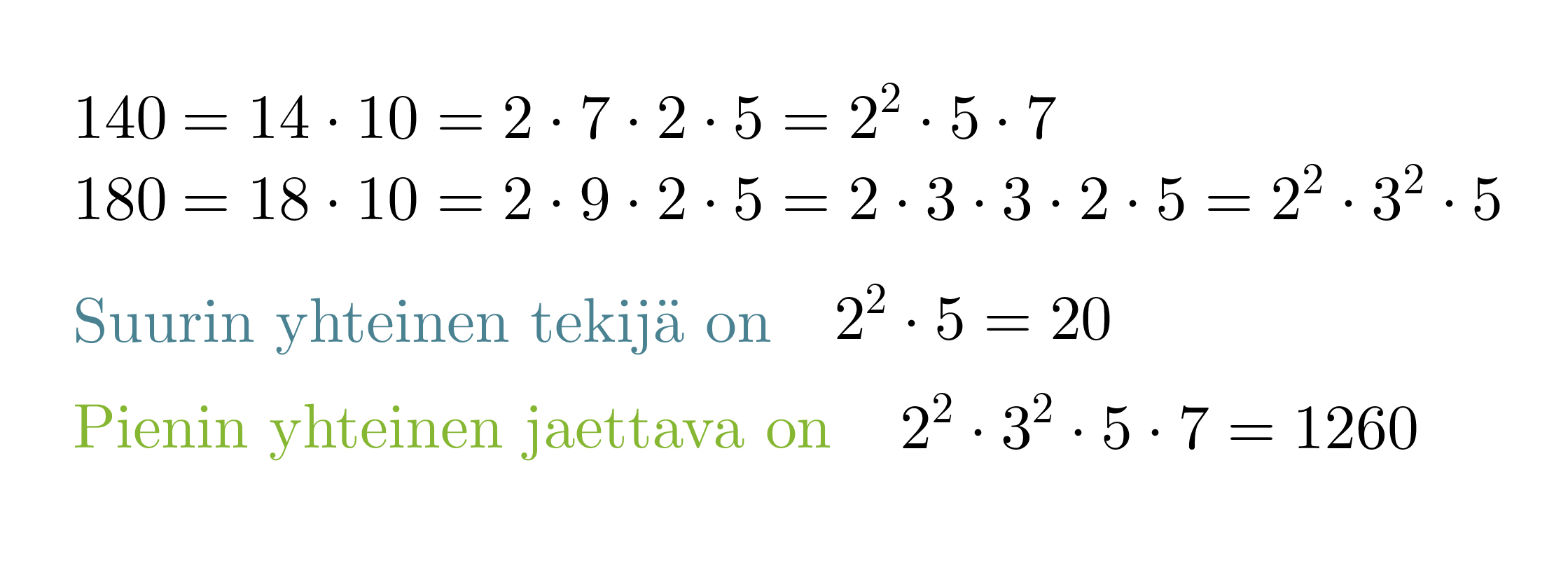
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Huom! Pienimmässä yhteisessä jaettavassa yhteiset tekijät huomioidaan ainoastaan kerran.
Jakamalla murtoluvun nimittäjä ja osoittaja alkutekijöihin, nähdään millainen desimaaliluku on kyseessä. Päättyvä desimaaliluku saadaan silloin, kun murtoluvun nimittäjän alkutekijöinä on murtoluvun supistetussa muodossa vain kakkosia tai viitosia. Jos nimittäjän alkutekijöinä on muita lukuja, on kyseessä päättymätön jaksollinen desimaaliluku.
Esimerkki 3.
Tutkitaan alkutekijöiden avulla minkälaiset desimaaliluvut ovat kyseessä.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!