3. Polynomit
Kertoimen ja muuttujaosan tuloa sanotaan termiksi.
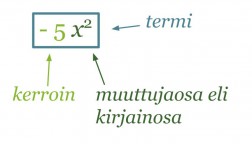
Klikkaa kuva suuremmaksi!
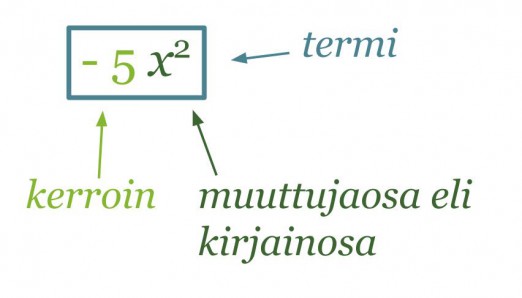
Klikkaa kuva suuremmaksi!
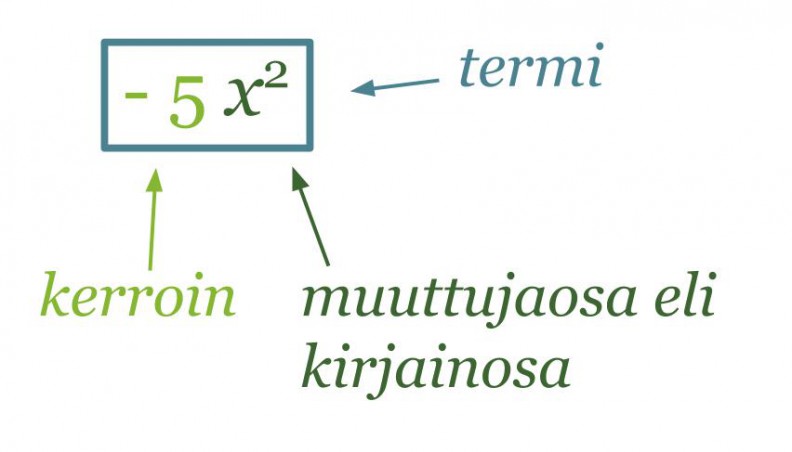
Klikkaa kuva suuremmaksi!
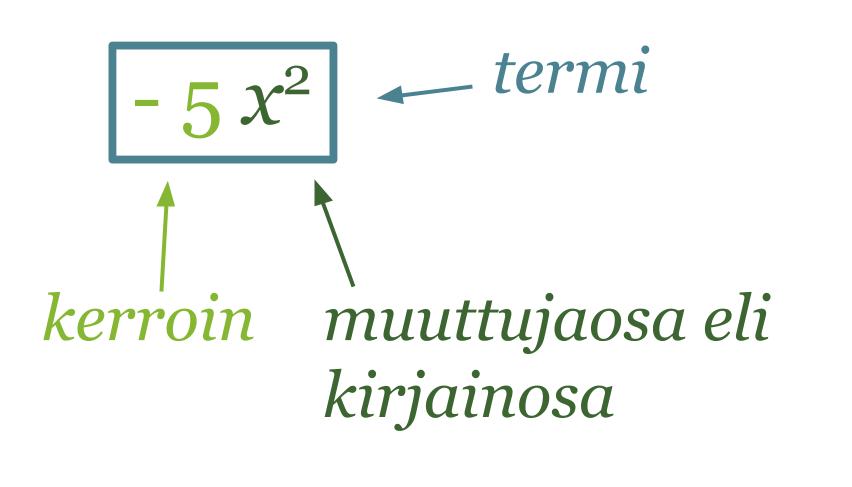
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Kun termejä lasketaan yhteen, muodostuu polynomi. Polynomia, jossa on vain yksi termi sanotaan monomiksi, kaksitermistä binomiksi ja kolmitermistä trinomiksi. Polynomin asteluvulla tarkoitetaan sen asteluvultaan korkeimman termin astelukua.
Polynomin termit järjestetään yleensä siten, että kirjainosien eksponentit pienenevät vasemmalta oikealle. Termiä, jossa ei ole muuttujaa, sanotaan vakioksi ja se kirjoitetaan viimeiseksi. Jos polynomissa on useita eri muuttujia, ne esitetään aakkosjärjestyksessä.
Esimerkki 1.
a) Polynomi 2x3 – x + 5 on trinomi
ja sen asteluku on 3.
b) Polynomi -2y on monomi
ja sen asteluku on 1.
c) Polynomi 4x2y + x on binomi
ja sen asteluku on 2.
Polynomin termit ovat samanmuotoisia, jos niillä on sama kirjainosa. Vain keskenään samanmuotoiset termit voidaan yhdistää yhteen- ja vähennyslaskussa.
Kahta polynomia, joiden summa on nolla, sanotaan toistensa vastapolynomeiksi. Polynomin vastapolynomi saadaan vaihtamalla polynomin jokaisen termin etumerkki.
Esimerkki 2.
Lasketaan polynomien erotus.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Polynomien kertolaskussa kerrotaan termit keskenään etumerkkeineen. Välivaiheita kannattaa merkitä näkyviin riittävästi.
Polynomien kertolasku
- Monomien kertolaskussa kertoimet kerrotaan keskenään ja muuttujaosat keskenään.
- Polynomi kerrotaan monomilla siten, että polynomin jokainen termi kerrotaan monomilla erikseen. Tulot lasketaan yhteen etumerkkeineen. a(b + c) = ab + ac
- Polynomien kertolaskussa jokaisella kertojan termillä kerrotaan jokainen kerrottavan termi. Saaudt tulot kirjoitetaan etumerkkeineen peräkkäin ja lasketaan yhteen. (a + b)(c + d) = ac + ad + dc + bd
Esimerkki 3.
Lasketaan monomien tulo.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
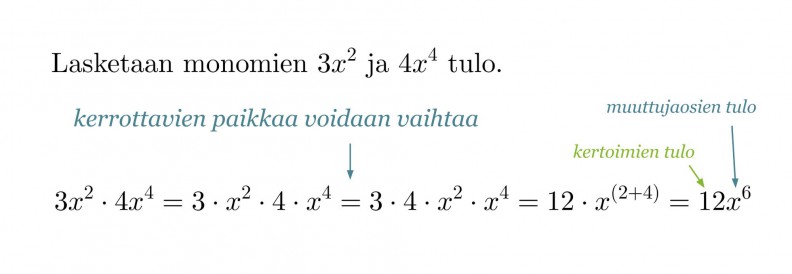
Klikkaa kuva suuremmaksi!
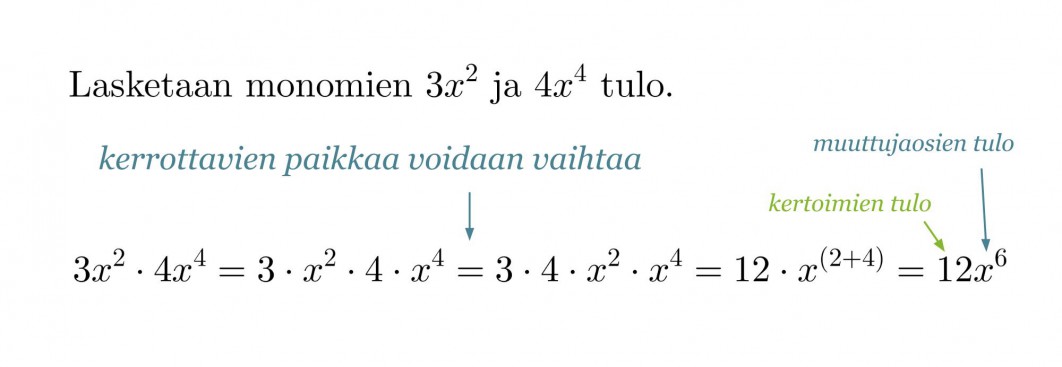
Klikkaa kuva suuremmaksi!
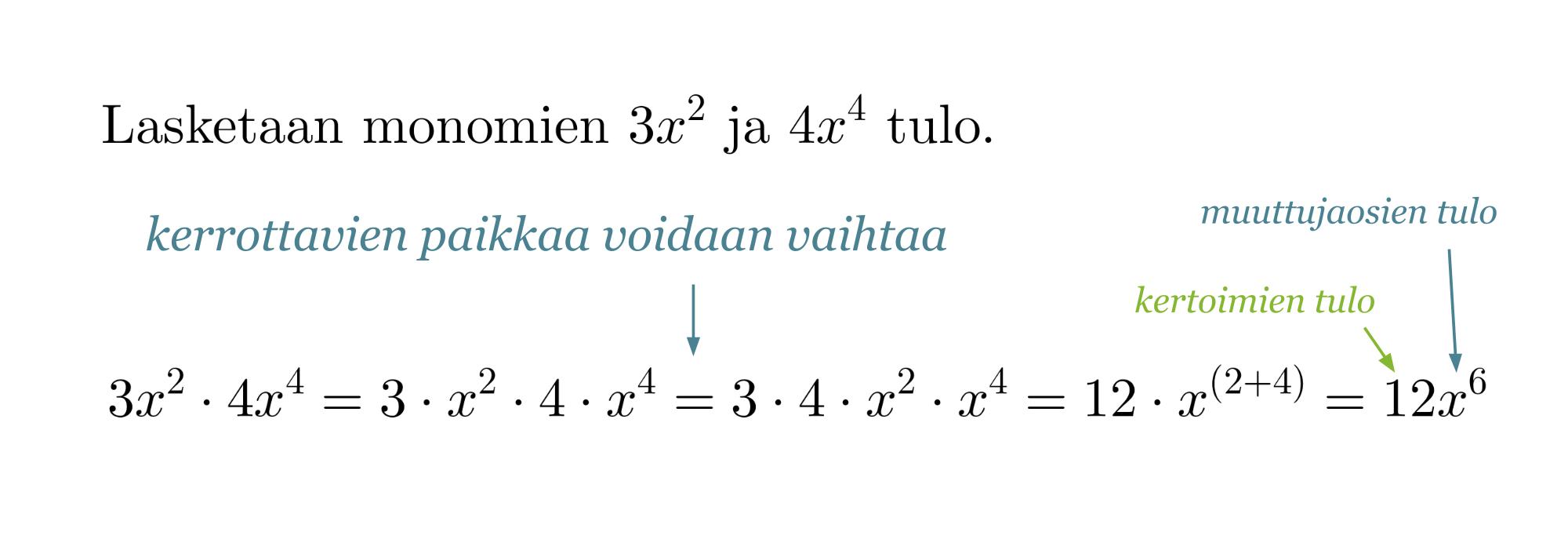
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 4.
Lasketaan monomin ja binomin tulo.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 5.
Lasketaan polynomien tulo.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Polynomien yhteen- ja vähennyslasku