4. Polynomin esittäminen tulona
Polynomien sieventäminen edellyttää usein tekijöihin jakoa, jolloin polynomi kirjoitetaan kahden tai useamman polynomin tulona. Polynomin ilmaiseminen tulona on erinomainen apu ratkaistaessa tietyn tyyppisiä toisen asteen yhtälöitä. Tällöin ratkaisut löytyvät tuttujen ensimmäisen asteen yhtälöiden ratkaisuina.
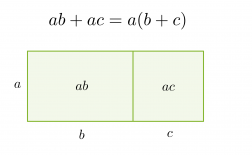
Jos jokaisessa polynomin termissä on sama tekijä, se voidaan erottaa yhteiseksi tekijäksi käyttämällä osittelulakia.
Klikkaa kuva suuremmaksi!
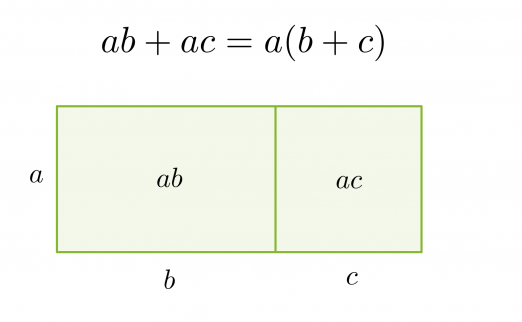
Klikkaa kuva suuremmaksi!
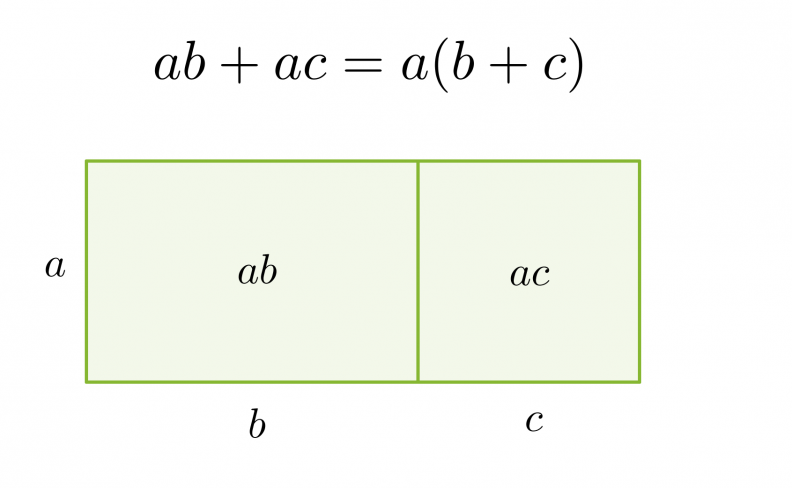
Klikkaa kuva suuremmaksi!
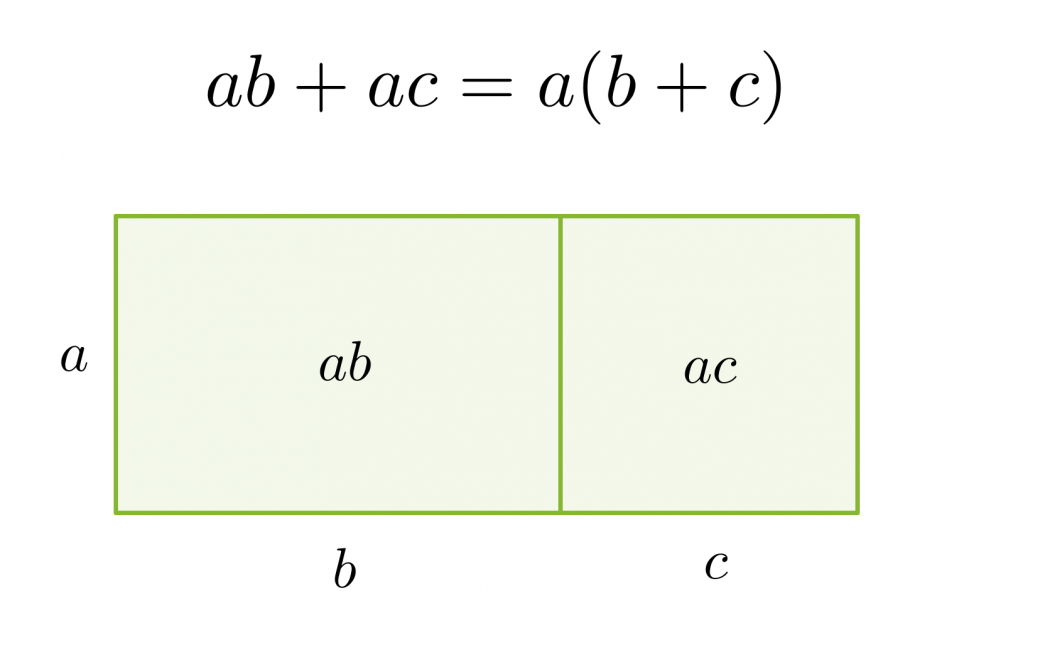
Klikkaa kuva suuremmaksi!
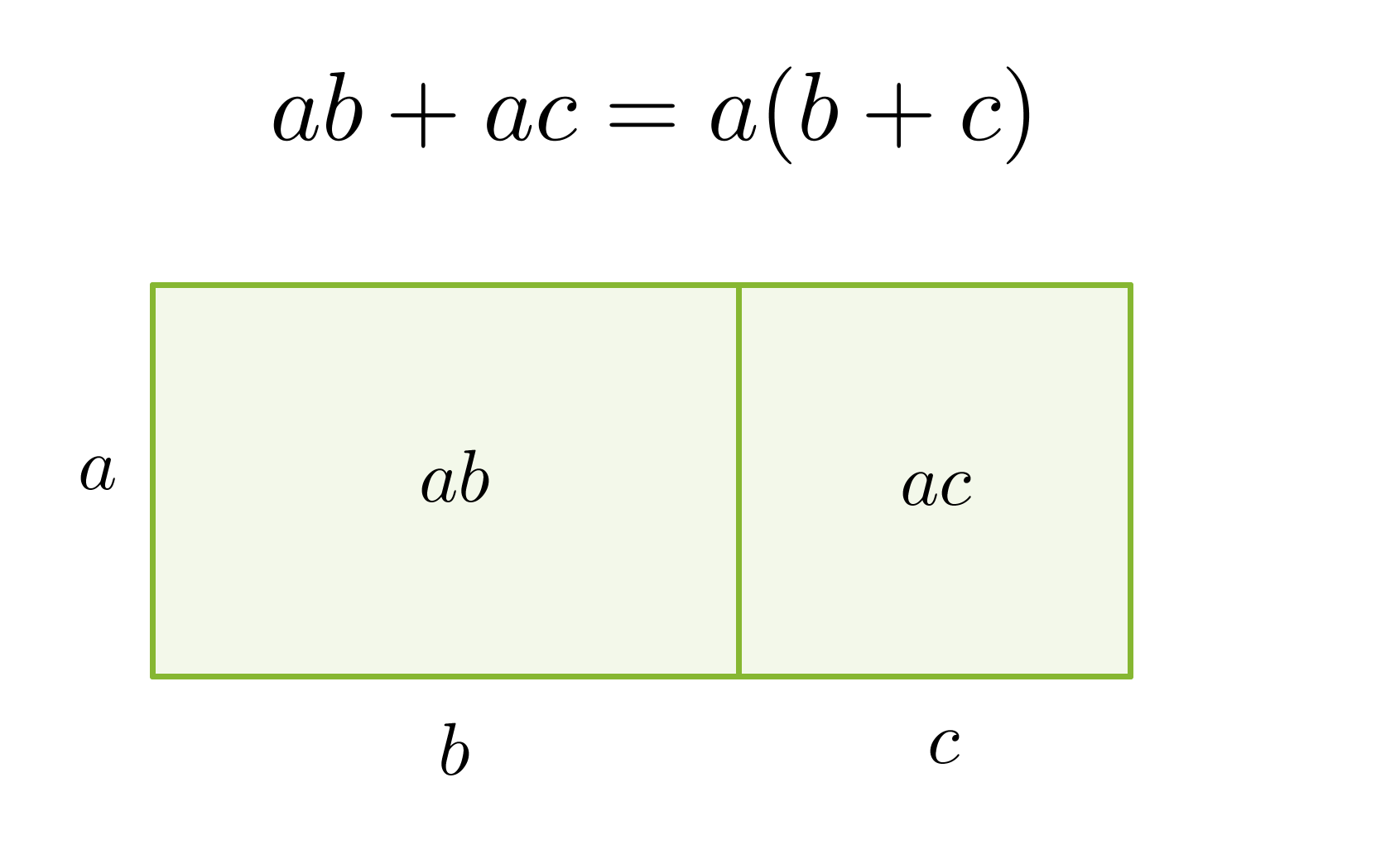
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tekijöihin jako on käänteinen toiminta sulkeiden poistamiselle lausekkeesta.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 1.
Jaetaan binomi tekijöihin.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Esimerkki 2.
Jaetaan trinomi tekijöihin.

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
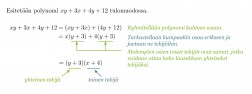
Esimerkki 3.
Esitetään polynomi tulomuodossa.
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
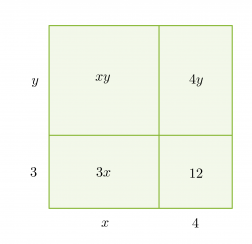
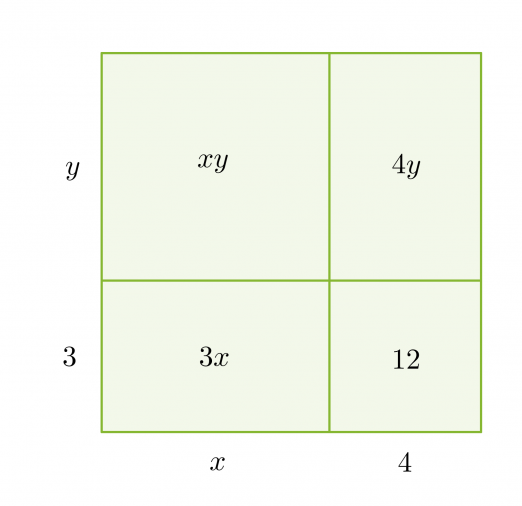
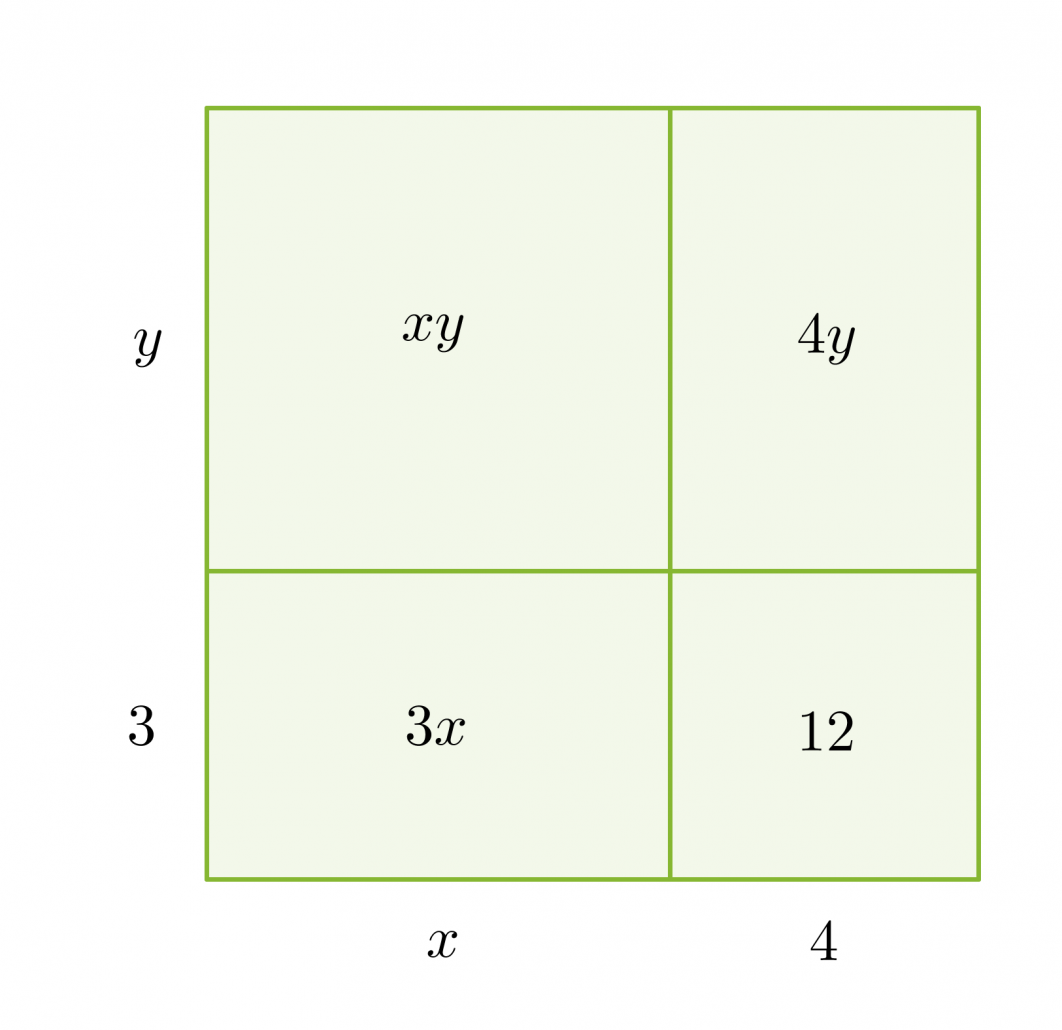
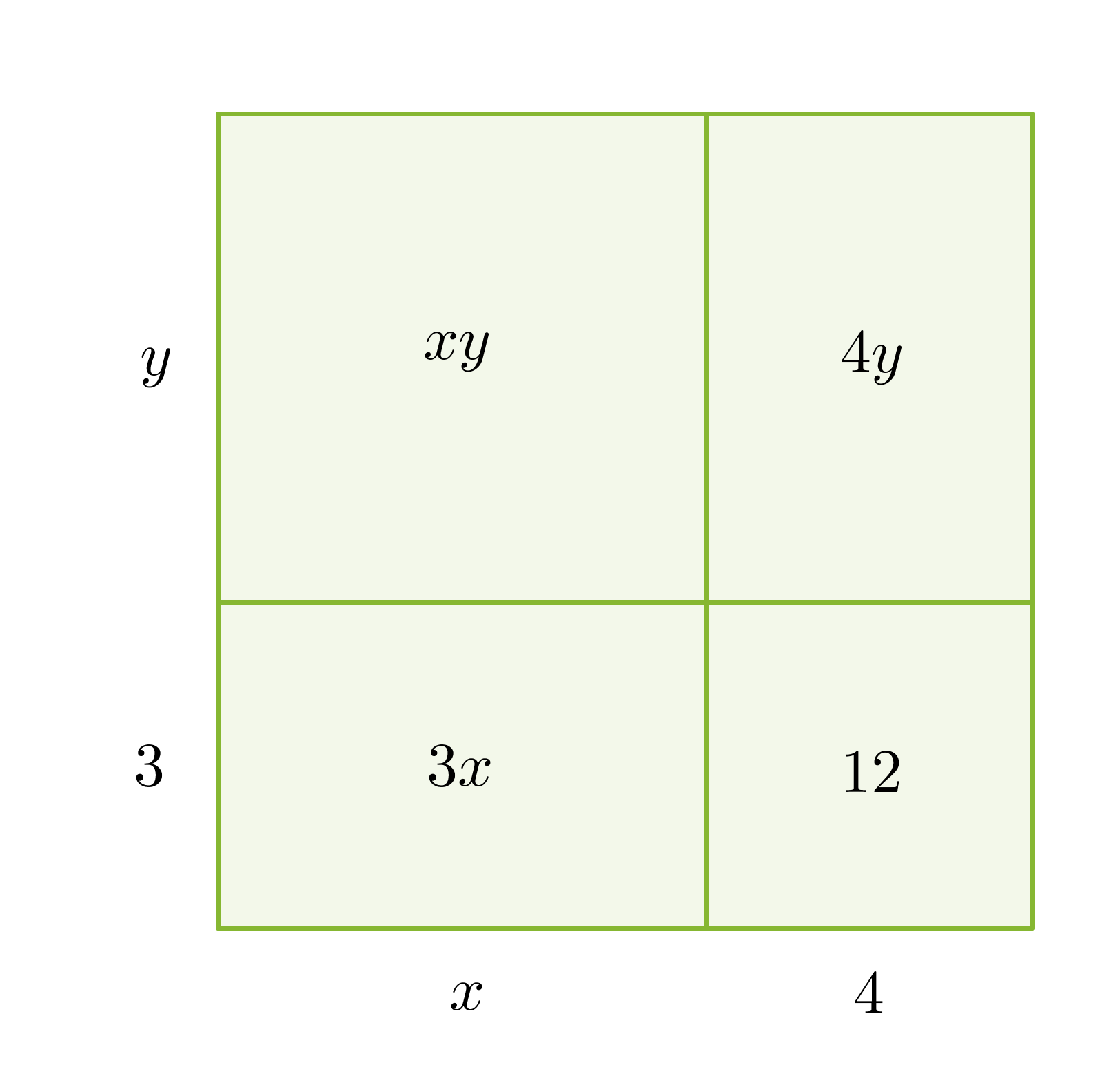
Tekijöihin jakoa voidaan havainnollistaa pinta-alamallin avulla. Jaetaan suorakulmion muotoinen alue neljään osaan ja sijoitetaan näistä kuhunkin yksi polynomin neljästä termistä.
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!
Klikkaa kuva suuremmaksi!

Klikkaa kuva suuremmaksi!
Tämän jälkeen tutkitaan mitä yhteistä on vierekkäisillä ja päällekkäisillä pinta-aloilla. Suorakulmion ala saadaan sivujen tulona, joka vastaa polynomin tekijöihin jakoa.
Avoin matematiikka 9Osio 3: Kerrataan ja sovelletaan5.6.2014